Grafuri

 

Introducere

Informatica este stiinta procesarii sistematice a informatiei. in special a procesarii cu ajutorul calculatoarelor. Istoric, informatica s-a dezvoltat ca stiinta din matematica, in timp ce dezvoltarea primelor calulatoare isi are originea in electrotehnica si telecomunicatii. De aceea, calculatorul reprezinta doar dispozitivul pe care sunt implementate conceptele teoretice. Informaticianul olandez Edsger Dijkstra afirma: 'In Informatica ai de-a face cu calculatorul, cum ai in astronomie cu telescopul'.

Termenul de 'informatica' provine din alaturarea cuvintelor 'informatie' si 'matematica'. Alte surse sustin ca provine din combinatia informatie si automatica.

Istoria stiintei calculatoarelor precede momentul aparitiei computerului digital. Inainte de anul 1920, termenul de 'computer' se referea ,in limba engleza, la un o persoana care efectua calcule (un functionar). Primii cercetatori in ceea ce avea sa se numeasca stiinta calculatoarelor, cum sunt Kurt Gdel, Alonzo Church si Alan Turing, au fost interesati de problema computationala: ce informatii ar putea un functionar uman sa calculeze avand hartie si creion, prin urmarirea pur si simplu a unei liste de instructiuni, atat timp cat este necesar, fara sa fie nevoie ca el sa fie inteligent sau sa presupuna capacitati intuitive. Una din motivatiile acestui proiect a fost dorinta de a proiecta si realiza 'masini computationale' care sa automatizeze munca, deseori plictisitoare si nu lipsita de erori, a unui computer uman.

In perioada anilor 1940, cand masinile computationale au cunoscut o evolutie accelerata, termenul de 'computer' si-a modificat semnificatia, referindu-se de acum mai degraba la masini, decat la predecesorii sai umani.

Informatica se divide in urmatoarele domenii fundamentale:

-informatica teoretica

-informatica practica

-informatica tehnica

Pe langa cele trei domenii mai exista si 'inteligenta artificiala' considerata o interdisciplina de sine statatoare.

Informatica teoretica se ocupa cu studiul 'teoriei limbajelor formale', respectiv automatica, 'teoria computationala si complexitatii','criptologie', 'logica','teoria grafurilor' s.a.m.d punand bazele pentru construirea compilatoarelor pentru limbajele de programare si pentru formalizarea problemelor din matematica. Ea este, prin urmare, coloana vertebrala a informaticii.

In matematica si informatica, 'teoria grafurilor' studiaza proprietatile grafurilor.

Grafuri- definitie

Numim graf o pereche ordonata de multimi, notata G=(X,U), unde X este o multime finita si nevida de elemente numite noduri sau varfuri, iar U este o multime de perechi (ordonate sau neordonate) de elemente din X numite muchii (daca sunt perechi neordonate) sau arce (daca sunt perechi ordonate). In primul caz, graful se numeste neorientat, altfel acesta este orientat.

Asadar un graf poate fi reprezentat sub forma unei figuri geometrice alcatuite din puncte (care corespund varfurilor) si din linii drepte sau curbe care unesc aceste puncte (care corespund muchiilor sau arcelor).

Grafurile au o importanta imensa in informatica, de exemplu:

-in unele problemele de sortare si cautare - elementele multimii pe care se face sortarea sau cautarea se pot reprezenta prin noduri intr-un graf;

-schema logica a unui program se poate reprezenta printr-un graf orientat in care o instructiune sau un bloc de instructiuni este reprezentat printr-un nod, iar muchiile directionate reprezinta calea de executie;

-in programarea orientata pe obiecte, ierarhia obiectelor (claselor) unui program poate fi reprezentata printr-un graf in care fiecare nod reprezinta o clasa, iar muchiile reprezinta relatii intre acestea (derivari, agregari).

Grafuri -Notiuni Generale

Grafurile se impart in doua categorii:

-grafuri neorientate;

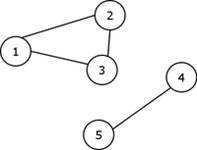
Fig. 1 - Graf neorientat

-grafuri orientate;

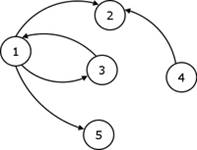
Fig. 2 - Graf orientat

Grafuri neorientate

Definitie. Se numeste graf neorientat o pereche ordonata de multimi (X, U), X fiind o multime finita si nevida de elemente numite noduri sau varfuri, iar U o multime de perechi neordonate ( submultimi cu doua elemente) din X, numite muchii.

Ex.

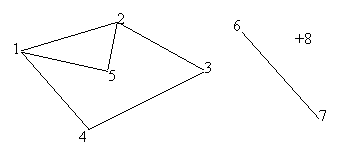
Fig.1

Pentru graful de mai sus avem:

X

U

Daca u₁ si u₂ sunt doua muchii care au o extremitate comuna ele se vor numi adiacente.

Definitie. Un graf partial al grafului G=(X,U) este un graf G₁=(X,V) astfel incat V U, adica G₁ are aceeasi multime de varfuri ca G iar multimea de muchii V este chiar U sau o submultime a acesteia.

Ex. Mai jos avem un graf partial al grafului de mai sus (Fig.1)

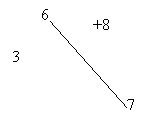
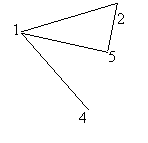
Fig.2

Cu alte cuvinte, un graf partial al unui graf se obtine pastrand aceeasi multime de varfuri si eliminand o parte din muchii.

Definitie. Un subgraf al unui graf G=(X,U) este un graf H=(Y,V) astfel incat Y X iar V contine toate muchiile din U care au ambele extremitati in Y. Vom spune ca subgraful H este indus sau generat de multimea de varfuri Y.

Ex. Mai jos avem un subgraf al grafului din Fig.1 obtinut prin eliminarea nodului 3

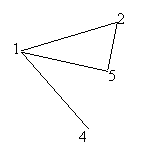
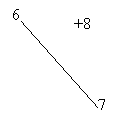
Definitie. Gradul unui varf x este numarul muchiilor incidente cu x.

Gradul varfului x se noteaza cu d(x).

Ex. in Fig.1 d(1)=3, d(4)=2, d(8)=0, d(6)=1

Un varf care are gradul 0 se numeste varf izolat.

Un varf care are gradul 1 se numeste varf terminal.

Propozitia 1. Daca un graf G=(X,U) are m muchii si n varfuri iar X=, atunci d(x₁)+d(x₂)++d(x_n)=2m.

Corolar. In orice graf G exista un numar par de varfuri de grad impar.

Definitie. Se numeste graf complet cu n varfuri un graf care are proprietatea ca orice doua noduri diferite sunt adiacente.

Propozitia 2. Un graf complet K_n are n(n-1)/2 muchii.

Definitie. Un graf G=(X,U) se numeste bipartit daca exista doua multimi nevide A, B astfel incat X=A U B, A B =F si orice muchie u a lui G are o extremitate in A iar cealalta in B.

Definitie. Un graf bipartit se numeste complet daca pentru orice x din A si orice y din B, exista in G muchia [x,y].

GRAFURI ORIENTATE

Un graf orientat G este format dintr-o pereche ordonata de multimi G=(X,U). ca si in cazul grafurilor neorientate, X este multimea varfurilor sau nodurilor grafului.Multimea U este formata din perechi ordonate de elemente distincte din X, numite arce.Orice arc uI U va fi notat prin u=(x,y) cu x,yIX si x y.

Spunem ca varful x este extremitatea initiala a arcului u, iar varful y este extremitatea finala a arcului u. Spre deosebire de cazul grafurilor neorientate, notatiile(x,y) si (y,x) vor desemna doua arce diferite.

Daca graful G contine arcul (x,y) vom spune ca varfurile x si y sunt adiacente in G si amandoua sunt incidente cu arcul (x,y). Deci, un graf orientat G poate fi imaginat ca o multime de varfuri, dintre care unele sunt unite doua cate doua prin arce. Un graf orientat poate fi desenat in plan reprezentand varfurile sale prin puncte si arcele prin sageti care sunt orientate de la extremitatea initiala catre extremitatea finala a fiecarui arc.

Graful orientat G=(X,U) unde:

X= si U= se reprezinta ca in figura:

2 u₅ 4

u₁

1 u₃ u₄ u₇

u₂

3 u₆ 5

Vom nota arcele asa cum se indica in figura , adica u₁=(1,2), u₂=(3,1),.., u₁₁=(6,8).

Gradul exterior al unui varf x, notat prin d(x), este numarul arcelor de forma (x,y) cu yIX. Gradul exterior al unui varf x, notat prin d-(x),este numarul arcelor de forma (y,x) cu yIX.

Un graf partial al unui graf orientat G=(X,U) se defineste in acelasi mod ca si in cazul neorientat. El este un graf G₁=(X,V) unde V U, deci este graful G insusi sau se obtine din G prin suprimarea anumitor arce.

Si definitia unui subgraf al unui graf orientat G=(X,U) este asemanatoare cu cazul neorientat.Prin definitie , un subgraf al lui G este un graf H=(Y,V), unde Y X, iar arcele din V sunt toate arcele din U care au ambele extremitati in multimea de varfuri Y.

Deci un subgraf H al unui graf orientat G este graful G insusi sau se obtine din G prin suprimarea anumitor varfuri si a tuturor arcelor incidente cu acestea .

Vom spune ca subgraful H este indus sau generat de multimea de varfuri Y.

Astfel,subgraful grafului G din figura ,indus de multimea de varfuri Y₁ = are ca multime de arce multimea V₁ =,iar subgraful indus de multimea de varfuri Y₂ = are multimea arcelor V₂=.

Un graf orientat este complet daca oricare doua varfuri sunt adiacente.

In timp ce in cazul neorientat un graf complet cu n varfuri este unic determinat, in cazul orientat exista mai multe grafuri complete cu un numar dat de varfuri.Ele se deosebesc fie prin orientarea arcelor , fie prin faptul ca intre doua varfuri oarecare exista un arc sau doua arce de sensuri contrare.

Un lant al unui graf orientat se defineste ca un sir de arce:

L=[u₁,u₂,...,u_p]

Cu proprietatea ca oricare arc u_I din acest sir are comuna o extremitate cu u_i- iar cealalta extremitate este comuna cu u_i+1 pentru orice i=1,,p-1.

Daca toate arcele lantului L au aceeasi orientare ,care este data de sensul deplasarii de la x₀ catre x_r lantul se numeste drum.

Deci un drum intr-un graf orientat G=(X,U) este un sir de varfuri notat :

D=(x_0,x1,,x_r)

cu proprietatea ca (x₀,x₁), (x_1,x₂), . , (x_r-1,x_r)IU, deci sunt arce ale grafului.

Varfurile x₀ si x_r se numesc extremitatile drumului D. Daca varfurile x₀ ,x₁ , , x_r sunt distincte doua cate doua, drumul D se numeste elementar. Din aceste definitii rezulta ca orice drum este si lant , daca il privim ca un sir de arce.

Un drum D=(x₀, ,x_r) poate fi interpretat ca fiind traseul unei daplasari pe arcele grafului in ordinea (x₀,x₁), (x₁,x₂), , (x_r-1,x_r).

De aceea drumul D de extremitati x₀ si x_r , se mai spune ca este un drum de la x₀ la x_r .Daca x₀=x_r si toate arcele (x₀,x₁), (x₁,x₂), ,(x_r-1,x_r) sunt distincte doua cate doua, drumul D se numeste circuit.

Daca toate varfurile circuitului, cu exceptia primului si a ultimului varf, sunt distincte doua cate doua, circuitul se numeste elementar.

Notiunile de conexitate si de componenta conexa a unui graf orientat sunt similare cu cele de la grafurile neorientate , utilizand notiunea de lant din cazul grafurilor orientate.

Astfel, un graf orientat G se numeste conex daca pentru oricare doua varfuri distincte x si y exista un lant de extremitati x si y in G. O componenta conexa C a unui graf orientat G se defineste ca fiind un subgraf conex maximal al lui G , deci nu exista nici un lant care sa uneasca un varf din C cu un varf care nu apartine lui C.

Numim ordinul unui graf, numarul de noduri al grafului, deci cardinalul multimii X(G), si notam aceasta valoare cu G Numarul de muchii se noteaza cu .

Graful vid este graful si se noteaza cu . Spunem ca un graf G este trivial daca acesta are ordinul 0 sau 1.

Spunem ca un nod v este incident cu o muchie r daca . Doua varfuri x si y se numesc adiacente daca exista o muchie e care le uneste (cu care amandoua varfurile sunt incidente). Doua muchii sunt adiacente daca exista un nod x care sa fie incident cu ambele muchii.

Numim gradul unui nod particular v , numarul de arce care sunt conectate la acel nod si se noteaza de obicei cu ρ(v) sau cud(v).

Daca adunam gradele tuturor nodurilor din graful G, obtinem de doua ori numarul de muchii:

Faptul ca membrul drept al ecuatiei va fi mereu par, implica aceeasi proprietate in membrul stang, pentru ca egalitatea sa fie satisfacuta.

Spunem ca un graf este conex daca intre oricare doua varfuri ale acestuia exista cel putin un drum. De exemplu grafurile din figurile 1 si 2 nu sunt conexe, in timp ce graful din figura 3 este un graf conex. Graful trivial este considerat conex.

Complementul unui graf G este graful , care contine o muchie intre varfurile x si y daca si numai daca G nu contine o astfel de muchie.

Complementul unui graf care nu este conex, este un graf conex. Reciproca nu este adevarata, de exemplu pentru un lant de lungime 3 (intre 4 varfuri).

Tipuri speciale de grafuri

Exista si tipuri speciale de grafuri

Acestea sunt:

-graful bipartit:

Fie G=(A,B) neorientat.

G este bipartit daca exista doua multimi, A₁ si A₂ astfel incat A₁ ∩ A₂ = si A₁ U A₂ = A, iar oricare muchie (x,y) apartinand lui B are un capat in multimea A₁ si celalalt in A₂.

Un graf bipartit este bipartit complet daca fiecare nod din multimea A₁ este adiacent cu toate nodurile din A₂ si reciproc.

-graful complet:

Graf complet

Un graf este complet daca oricare doua varfuri distince sunt adiacente.

Un graf neorientat cu n noduri are n(n-1)/2 muchii.

Exista un singur graf complet neorientat cu n noduri.

Exista mai multe grafuri orientate complete cu n noduri.

-graful hamiltonian:

Grafuri hamiltoniene

Lant hamiltonian: lant elementar care contine toate nodurile grafului.

Ciclu hamiltonian: ciclu elementar care contine toate nodurile grafului.

Graf hamiltonian: graf care contine un ciclu hamiltonian.

Conditii de suficienta:

Teorema lui Dirac: Fie G dat prin perechea (A,B). Daca G are un numar de cel putin 3 varfuri astfel incat gradul fiecarui nod respecta conditia d(x)≥n/2, atunci graful este hamiltonian.

Algoritmi de determinare a unei solutii

Algoritmul utilizat este Backtracking, care este adaptat in mod corespunzator.

-graful eulerian: Grafuri euleriene

Ciclu eulerian: ciclu care trece prin toate muchiile unui graf exact o data.

Graf eulerian: graf care contine cel putin un ciclu eulerian.

Conditii de suficienta

Teorema: Fie un graf conex fara noduri izolate cu n≥ 3 noduri. Graful este eulerian daca si numai daca pentru oricare nod al sau, x, d(x) este par.

Determinarea unui ciclu eulerian

• Se porneste de la un nod oarecare si se construieste un ciclu.
• Se parcurg nodurile din ciclul determinat anterior; daca exista un nod care mai are muchii neincluse in ciclul anterior se construieste un nou ciclu provenind de la acest nod.
• Ciclul construit este inclus in ciclul initial in locul nodului gasit la pasul anterior.

• pas 1:
• c1: 1,2,3,1
• c2: 2,4,7,2
• pas 2:
• c1: 1,2,4,7,2,3,1
• c2: 7,5,10,7
• pas 3:
• c1: 1,2,4,7,5,10,7,2,3,1
• c2: 7,8,11,7
• pas 4:
• c1: 1,2,4,7,8,11,7,5,10,7,2,3,1
• c2: 7,6,9,7
• pas 5:
• c1: 1,2,4,7,6,9,7,8,11,7,5,10,7,2,3,1

-arbori:

Fie G un graf orientat. G este un arbore cu radacina r, daca exista in G un varf r din care oricare alt varf poate fi ajuns printr-un drum unic.

Definitia este valabila si pentru cazul unui graf neorientat, alegerea unei radacini fiind insa in acest caz arbitrara: orice arbore este un arbore cu radacina, iar radacina poate fi fixata in oricare varf al sau. Aceasta, deoarece dintr-un varf oarecare se poate ajunge in oricare alt varf printr-un drum unic.

Cand nu va fi pericol de confuzie, vom folosi termenul "arbore", in loc de termenul corect "arbore cu radacina". Cel mai intuitiv este sa reprezentam un arbore cu radacina, ca pe un arbore propriu-zis. In Figura 3.1, vom spune ca beta este tatal lui delta si fiul lui alpha, ca beta si gamma sunt frati, ca delta este un descendent al lui alpha, iar alpha este un ascendent al lui delta. Un varf terminal este un varf fara descendenti. Varfurile care nu sunt terminale sunt neterminale. De multe ori, vom considera ca exista o ordonare a descendentilor aceluiasi parinte: beta este situat la stanga lui gamma, adica beta este fratele mai varstnic al lui gamma.

Orice varf al unui arbore cu radacina este radacina unui subarbore constand din varful respectiv si toti descendentii sai. O multime de arbori disjuncti formeaza o padure.

Intr-un arbore cu radacina vom adopta urmatoarele notatii. Adancimea unui varf este lungimea drumului dintre radacina si acest varf; inaltimea unui varf este lungimea celui mai lung drum dintre acest varf si un varf terminal; inaltimea arborelui este inaltimea radacinii; nivelul unui varf este inaltimea arborelui, minus adancimea acestui varf.

Reprezentarea unui arbore cu radacina se poate face prin adrese, ca si in cazul listelor inlantuite. Fiecare varf va fi memorat in trei locatii diferite, reprezentand informatia propriu-zisa a varfului (valoarea varfului), adresa celui mai varstnic fiu si adresa urmatorului frate. Pastrand analogia cu listele inlantuite, daca se cunoaste de la inceput numarul maxim de varfuri, atunci implementarea arborilor cu radacina se poate face prin tablouri paralele

Au fost studiate diferite tipuri de arbori binari, adica arbori pentru care e-gradul fiecarui nod este mai mic sau egal cu 2. Arborii care au e-gradul mai mare sau egal cu 2 se numesc arbori multicai.

Daca se doreste sa se prezinte descendenta unei persoane din punct de vedere al stramosilor, i se asociaza persoanei doi parinti, obtinandu-se un arbore binar.

Se considera problema construirii si explorarii informatiei continute in arbori de mari dimensiuni; se considera si operatiile executate unor astfel de arbori.

Sa notam ca astfel de arbori sunt pastrati pe suporturi auxiliare; atunci nodurile arborelui sunt memorate pe un suport auxiliar si sunt transferate pe rand sau pe grupe in memoria centrala.

Structurile dinamice sunt cele utilizate eficient pentru implementarea unor astfel de arbori. In acest caz pointerii nodurilor nu vor mai indica adrese de memorie.

Utilizand un arbore cu 10⁶ noduri, vor fi necesare aproximativ log₂10⁶ pasi pentru cautarea unor elemente.

Deoarece fiecare pas necesita un acces la memoria auxiliara rezulta necesitatea unei organizari care sa reduca numarul de accese.

Este stiut faptul ca dupa realizarea accesului la un anumit element al memoriei auxiliare este usor accesibil fiecare element al arborelui din zona respectiva. Acest lucru sugereaza ca un arbore poate fi divizat in subarbori ce pot fi reprezentati ca unitati la care accesul se realizeaza deodata. Subarborii in care sunt divizati arborii de mari dimensiuni si care au proprietatea de mai sus se numesc pagini.

Pentru descompunerea in pagini a unui arbore binar trebuie avute in vedere urmatoarele aspecte:

a) modul de grupare a cheilor intr-un arbore multicai;

b) modul de plasare a elementelor corespunzatoare diverselor chei;

c) tehnica de inserare sau eliminare a unei chei;

d) modul de aranjare a cheilor in cadrul unui nod.

Dintre toate modurile de organizare a arborilor multicai cel mai eficient este arborele 3-2, care reprezinta o varianta de arbore echilibrat; un nod al unui astfel de arbore poate avea cel mult 3 descendenti directi.

Matricea de adiacenta

A. Pentru grafuri neorientate

 a[i,j] = 1, daca intre i si j este muchie

 a[i,j] = 0 altfel.

Observatie: Pe diagonala principala toate elementele sunt 0 (nu avem bucle).

Matricea este simetrica fata de diagonala principala, deci: a[i,j] = a[j,i].

B. Pentru grafuri orientate

 a[i,j] = 1, daca exista arcul (i,j);

 a[i,j] = 0, altfel.

2. Liste de adiacenta

Pentru fiecare nod se memoreaza o lista a vecinilor sai.

Pentru intregul graf este necesar un vector de liste (P) in care P_i este adresa primului element al listei asociate lui i.

		Nod Lista de adiacenta asociata

De exemplu, pentru i = 1, informatia din lista figurata mai sus se va completa astfel: p[1] - 2 - 3 - 5.

Nod Lista de adiacenta asociata

Observatie: pentru grafurile orientate se memoreaza in lista lui i nodurile k pentru care exista arcul (i,k).

4. Matricea noduri-arce

Este folosita in special pentru grafurile orientate.

Observatie: matricea noduri-arce poate fi adaptata si pentru grafurile neorientate.