| CATEGORII DOCUMENTE |
O schema logica este un desen care descrie multimea pasilor ce constituie un proces de calcul. Folosind schemele logice devine posibila reprezentarea secventelor care compun codul unui program. Schemele logice utilizeaza in acest scop sageti de legatura intre diferite simboluri geometrice care simbolizeaza tipurile de actiuni.
Schemele logice sunt folosite pentru dezvoltarea de software; ele sunt realizate inainte de a fi scris programul sursa, cu scopul de a detalia logica solutiei si de a simplifica munca de scriere a codului. Folosite in acest scop, schemele logice functioneaza ca:
Mijloc de documentare
Instrument de analiza
Mijloc de comunicare
Schemele logice sunt, prin natura lor, diagrame simbolice. Astfel, ele sunt compuse din simboluri care specifica operatii bine-definite. Fiecare simbol este unic ca forma si reprezinta o anumita operatie, avand pozitia fixata in interiorul schemei logice si fiind conectat la simbolurile de inaintea lui si de dupa el. Aceasta multime de simboluri creeaza succesiunea pasilor care definesc lista operatiilor pe care le contine programul (Figura 5.1).
Presupunem ca programul actioneaza asupra unor date aflate pe o banda de intrare, iar rezultatele sint inregistrate pe o banda de iesire. Modul de acces si organizare pentru mediile de intrare si iesire este cel secvential.
Sunt admise urmatoarele instructiuni:
1. Instructiunea START. Executia unui program incepe intotdeauna cu aceasta instructiune.
2. Instructiunea STOP. Efectul acestei instructiuni este terminarea executiei programului.
3. Instructiunea de citire, care determina citirea a n valori de pe banda de intrare si inscrierea lor in locatiile de memorie rezervate pentru variabilele a1, , an.
4. Instructiunea de scriere, care determina inscrierea pe banda de iesire a valorilor memorate in locatiile de memorie rezervate pentru valorile a1, , an.
5. Instructiunea de atribuire, al carei efect consta in evaluarea expresiei e si inscrierea rezultatului in locatia de memorie rezervata variabilei v.
6. Instructiunea de ramificare. Efectul instructiunii consta in continuarea calculelor mergand pe sageata corespunzatoare unei alternative unice din mai multe.
|
Simbol |
nume |
utilizare |
|
|
Bloc terminal |
START, STOP |
|
Bloc de calcul |
Indica procesele de calcul |
|
|
Bloc de decizie |
Indica ramificatiile functie de o anumita conditie ce se va scrie in interiorul sau. |
|
|
Bloc conector |
Indica punctul de sfarsit al unei structuri alternative, sau punctul de inceput al unei structuri repetitive. |
|
|
Sageata |
Indica inlantuirea blocurilor intr-o schema logica. |
|
|
Bloc de procedura |
Reprezinta o prescurtare corespunzatoare catorva pasi dintr-o schema logica. |
|
|
Bloc de intrare / iesire |
READ, WRITE |
Figura 5.1 Simbolurile grafice din scheme logice
Schematic aceste instructiuni se reprezinta in modul urmator:
1. Instructiunile START si STOP:
Simbolul utilizat pentru aceste instructiuni este blocul terminal (Figura 5.2). Blocul terminal este folosit pentru a indica inceputul si sfarsitul unei scheme logice. O conventie in alcatuirea schemelor logice impune ca numai doua blocuri terminale sa poata fi plasate intr-o schema logica, unul la inceputul si celalalt la sfarsitul acesteia.
Aceeasi conventie impune si ca blocurile terminale folosite sa fie obligatoriu marcate prin cuvintele START si STOP, corespunzatoare blocului de inceput si respectiv de sfarsit al schemei logice. Blocurile terminale astfel marcate sunt cunoscute si sub numele de bloc START, respectiv bloc STOP.

2. Instructiunile de intrare / iesire:
Realizarea operatiilor de intrare si de iesire este marcata prin folosirea blocurilor de intrare / iesire. Pentru a indica operatia de intrare se folosesc cuvintele READ sau INPUT, iar pentru a indica operatia de iesire se folosesc cuvintele WRITE sau OUTPUT.
Pentru standardizare, vom folosi numai una dintre aceste optiuni, si anume cuvantul READ pentru operatia de intrare (introducere de date), respectiv cuvantul WRITE pentru operatia de iesire (scriere de date). Aceste notatii sunt apropiate de limbajul BASIC, ceea ce usureaza o eventuala conversie a schemei logice in program BASIC. Se practica si o prescurtare, astfel incat blocurile de intrare / iesire astfel marcate sunt cunoscute si sub numele de blocuri READ, respectiv WRITE (Figura 5.3).
INPUT OUTPUT
a1, a2,.an a1, a2,.an
READ WRITE
a1, a2,.an a1, a2,.an

Figura 5.3 Blocurile de intrare / iesire (I/O)
3. Instructiunea de atribuire (de calcul):
Blocul de calcul este folosit pentru a indica operatii de calcul - care presupun manipularea aritmetica a datelor, sau operatii de atribuire - care presupun , pe langa calcul, si mutarea datelor dintr-o locatie de memorie in alta.
Intr-un astfel de bloc de calcul se inscriu formule matematice, sau propozitii care precizeaza calculele ce urmeaza a fi efectuate (Figura 5.4).
V e i i + 1
![]()
Figura 5.4 Blocul de calcul
4. Instructiunea de decizie:
Blocul de decizie este folosit atunci cand vrem sa efectuam pasi diferiti, dependenti de o anumita conditie; cand conditia este adevarata vom efectua o secventa de instructiuni, iar cand conditia este falsa vom efectua o alta secventa de instructiuni. Este posibil si cazul in care conditia poate fi evaluata la mai multe valori posibile; atunci vom realiza operatii diferite pentru fiecare valoare in parte.
Astfel in program sunt introduse ramificatii, functie de evaluarea conditiei. In acest caz se poate opta pentru o varianta din mai multe posibile (Figura 5.5).
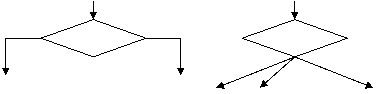
conditie conditie
DA NU
P1 P2 . Pn
Figura 5.5 Blocul de decizie
Vom numi schema logica o reprezentare grafica in care:
1. exista o unica instructiune START si o unica instructiune STOP
2. este alcatuita numai din instructiuni de tipul:
- STOP, START
- o citire sau o scriere
- o atribuire
- o ramificare
3. exista macar un drum care incepe cu instructiunea START si se termina cu instructiunea STOP
Schemele logice permit precizarea actiunilor algoritmului prin enunturi asociate simbolurilor grafice.
Definitia de mai sus nu poate elimina insa toate cazurile de nedeterminare a programelor, cum ar fi de exemplu o schema logica de felul celei din Figura 5.6, care face ca programul sa cicleze pe aceste comenzi, adica sa se execute la infinit.
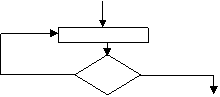
x
DA x = 1 ? NU
Figura 5.6 Un caz de nedeterminare in scheme logice
Un exemplu de schema logica creata pentru a rezolva o problema este prezentat la sfarsitul acestei sectiuni (Figura 5.7).
Pentru a usura construirea si citirea schemelor logice s-a simtit nevoia ca in constructia acestora sa se foloseasca numai anumite configuratii obtinandu-se astfel scheme logice structurate, care respecta definitia enuntata mai sus. Aceste structuri sint specifice programarii structurate.
In maniera 'traditionala' de alcatuire a algoritmilor, realizarea diferitelor structuri de control se bazeaza pe utilizarea unor comenzi de salt conditionat si neconditionat, dand programatorilor o mare libertate in alcatuirea algoritmilor. Rezultatul a fost ca algoritmii contineau un numar important de salturi 'nedisciplinate' care ascundeau rationamentele, ingreunand intelegerea, testarea si modificarea programelor scrise pe baza lor.
Pentru a ocoli aceste neajunsuri, programarea structurata propune disciplinarea realizarii algoritmilor prin restrangerea structurilor de control utilizate la un anumit set redus de tipuri de structuri. Orice algoritm, oricat de complex, urmeaza a fi realizat numai printr-o combinatie de structuri din acest set, incluse una in alta.
Programarea structurata are la baza o justificare matematica furnizata de Bhm si Jacopini in 1966, cunoscuta ca 'teorema de structura', care precizeaza ca orice algoritm avand o intrare si o iesire poate fi reprezentat ca o combinatie de trei structuri de control:
- secventa de doua sau mai multe operatii (enumerare);
- alegerea unei operatii din doua alternative posibile (decizie);
- repetarea unor operatii atat timp cit o anumita conditie este indeplinita (ciclul cu test initial, iteratie).
Efectele structurilor descrise corespund unor procese ale rationamentului uman: enumerarea, decizia, iteratia, ceea ce face ca utilizarea lor in dezvoltarea algoritmilor sa fie deosebit de simpla si naturala.
O alta teorema care sta la baza programarii structurate este teorema de rafinare si descompunere; aceasta ne spune ca asezand intr-un nod al unei scheme logice o alta schema logica, rezultatul este tot o schema logica si faptul ca o schema logica poate fi descompusa in subscheme logice mai mici pe care se lucreaza separat ca apoi sa le reimbinam. Aceasta conduce si la un alt mod de programare, si anume la programarea modulara.
Dar problemele complexe din viata reala nu pot fi reprezentate totdeauna prin schemele logice care nu au posibilitatea de declarare a tipurilor, si de la un anumit nivel devin greu de urmarit - cand este vorba de rezolvarea unor probleme foarte complexe. In astfel de situatii se utilizeaza un alt limbaj de descriere al algoritmilor, si anume limbajul pseudocod.
Exemplu de schema logica:
Ne propunem sa construim o schema logica corespunzatoare rezolvarii urmatoarei probleme:
"Se introduc cinci date de intrare (valori numerice) A, B, C, D, E si se doreste calcularea valorilor urmatoare:
X = A + B + C + D + E
Y = E + (B + C)/A + 1/D."
Schema logica corespunzatoare va fi:
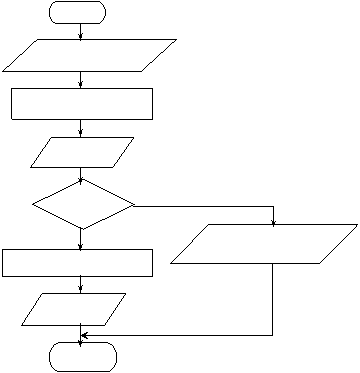
START
READ A, B, C, D, E
X A + B + C + D + E
WRITE X
A D ¹ 0 ? NU
DA WRITE
"Nu se poate calcula Y"
Y E + (B + C)/A + 1/D
Figura
5.7 Exemplu de schema logica
WRITE Y
STOP
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6040
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved