Liste

class elem

elem(char ch)

elem adaug(char ch)

void creare()

}

String direct(elem x)

String invers(elem x)

class Lista

unde operatorul are sensul 'diferit de'.

Sa presupunem ca la intrare apare: abc$c1 La iesire vom obtine:

abc

cba

Arbori

Numim arbore un graf neorientat conex si fara cicluri.

Aceasta nu este singurul mod in care putem defini arborii. Cateva definitii echivalente apar in urmatoarea teorema, expusa fara demonstratie.

Teorema. Fie G un graf cu n varfuri. Urmatoarele afirmatii sunt echivalente:

G este un arbore;

G are n-1 muchii si nu contine cicluri;

G are n-1 muchii si este conex;

oricare doua varfuri din G sunt unite printr-un unic drum;

G nu contine cicluri si adaugarea unei noi muchii produce un unic ciclu elementar;

G este conex, dar devine neconex prin stergerea oricarei muchii.

In foarte multe probleme referitoare la arbori este pus in evidenta un varf al sau, numit radacina. Alegerea unui varf drept radacina are doua consecinte:

Arborele poate fi asezat pe niveluri astfel:

radacina este asezata pe nivelul 0;

pe fiecare nivel i sunt plasate varfurile pentru care lungimea drumurilor care le leaga de radacina este i

se traseaza muchiile arborelui.

Aceasta asezare pe niveluri face mai intuitiva notiunea de arbore, cu precizarea ca in informatica 'arborii cresc in jos'.

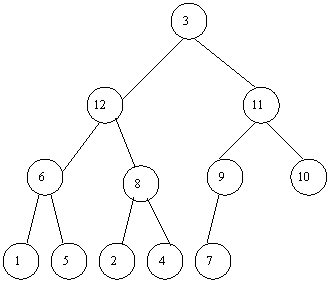
Exemplul 3. Consider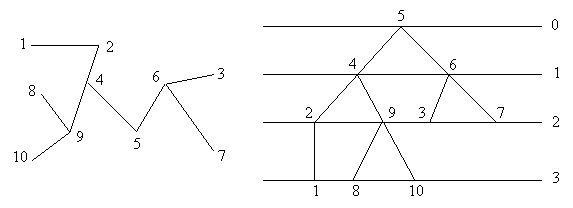am urmatorul arbore si modul in care el este asezat pe niveluri prin alegerea varfului 5 drept radacina.

Arborele poate fi considerat un graf orientat, stabilind pe fiecare muchie sensul de la nivelul superior catre nivelul inferior.

Reprezentarea pe niveluri a arborilor face ca notiunile de fii (descendenti) ai unui varf, precum si de tata al    unui varf sa aiba semnificatii evidente. Un varf fara descendenti se numeste frunza.

Arbori binari

Un arbore binar este un arbore in care orice varf are cel mult doi descendenti, cu precizarea ca se face distinctie intre descendentul stang si cel drept. Din acesta definitie rezulta ca un arbore binar nu este propriu-zis un caz particular de arbore.

Primele probleme care se pun pentru arborii binari (ca si pentru arborii oarecare si pentru grafuri, asa cum vom vedea mai tarziu) sunt:

modul de reprezentare;

parcurgerea lor.

Forma standard de reprezentare a unui arbore binar consta in:

a preciza radacina rad a arborelui;

a preciza pentru fiecare varf i tripletul st(i) dr(i) si info(i), unde acestea sunt respectiv descendentul stang, descendentul drept si informatia atasata varfului.

Trebuie stabilita o conventie pentru lipsa unuia sau a ambilor descendenti, ca de exemplu specificarea lor prin simbolul l

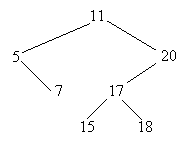
Exemplul 4. Consideram de exemplu urmatorul arbore binar:

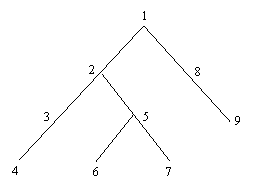
Presupunand ca informatia atasata fiecarui varf este chiar numarul sau de ordine, avem:

rad = 1

st    = (2,3,4,l l l l l

dr    = (8,5,l l l l l

info= (1,2,3,4,5,6,7,8,9)

Dintre diferitele alte reprezentari posibile, mai mentionam doar pe cea care se reduce la vectorul sau tata si la vectorul info. Pentru exemplul de mai sus:

tata=(l

Problema parcurgerii unui arbore binar consta in identificarea unei modalitati prin care, plecand din radacina si mergand pe muchii, sa ajungem in toate varfurile; in plus, atingerea fiecarui varf este pusa in evidenta o singura data: spunem ca vizitam varful respectiv. Actiunea intreprinsa la vizitarea unui varf depinde de problema concreta si poate fi de exemplu tiparirea informatiei atasate varfului.

Distingem trei modalitati standard de parcurgere a unui arbore binar:

Parcurgerea in preordine

Se parcurg recursiv in ordine: radacina, subarborele stang, subarborele drept.

Concret, se executa apelul preord(rad) pentru procedura:

procedure preord(x)

if x=l

then

else vizit(x); preord(st(x)); preord(dr(x))

end

Ilustram acest mod de parcurgere pentru exemplul de mai sus, figurand ingrosat radacinile subarborilor ce trebuie dezvoltati:

Parcurgerea in inordine

Se parcurg recursiv in ordine: subarborele stang, radacina, subarborele drept.

Ilustram acest mod de parcurgere pentru Exemplul 4:

Concret, se executa apelul inord(rad) pentru procedura:

procedure inord(x)

if x=l

then

else inord(st(x)); vizit(x); inord(dr(x))

end

Parcurgerea in postordine

Se parcurg recursiv in ordine; subarborele stang, subarborele drept, radacina.

Ilustram parcurgerea in postordine pentru Exemplul 4:

Concret, se executa apelul postord(rad) pentru procedura:

procedure postord(x)

if x=l

then

else postord(st(x)); postord(dr(x)); vizit(x)

end

Sortarea cu ansamble

Fie a=(a₁,.,a_n) vectorul care trebuie sortat (ordonat crescator).

Metoda sortarii de ansamble va folosi o reprezentare implicita a unui vector ca arbore binar. Acest arbore este construit succesiv astfel:

radacina este 1;

pentru orice varf descendentii sai stang si drept sunt 2i si 2i+1 (cu conditia ca fiecare dintre aceste valori sa nu depaseasca pe n). Rezulta ca tatal oricarui varf i este tata(i)= i/2

Evident, fiecarui varf i ii vom atasa eticheta a_i

Pentru 2^k-1 n<2^k arborele va avea k niveluri, dintre care numai ultimul poate fi incomplet (pe fiecare nivel i<k-1 se afla exact 2ⁱ varfuri).

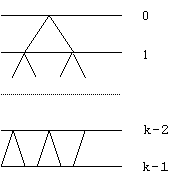
Vectorul a se numeste ansamblu daca pentru orice i avem a_i a_2i si a_i a_2i+1 (daca fiii exista).

Sa presupunem ca subarborii de radacini 2i si 2i+1 sunt ansamble. Ne propunem sa transformam arborele de radacina i intr-un ansamblu. Ideea este de a retrograda valoarea a_i pana ajunge intr-un varf ai carui descendenti au valorile mai mici decat a_i. Acest lucru este realizat de procedura combin

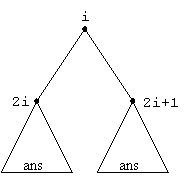
procedure combin(i,n)

i 2i; b a_i

while j n

if j<n & a_j<a_j+1 then j j+1

if b>a_j

then a _j/2 b; exit

else a _j/2 a_j; j 2j

a _j/2 b

end

Timpul de executare pentru procedura combin este O(k)=O(log n)

Sortarea vectorului a se va face prin apelul succesiv al procedurilor creare si sortare prezentate mai jos.

Procedura creare transforma vectorul intr-un ansamblu; in particular in a₁ se obtine cel mai mare element al vectorului.

Procedura sortare lucreaza astfel:

pune pe a₁ pe pozitia n si reface ansamblul format din primele n-1 elemente;

pune pe a₁ pe pozitia n-1 si reface ansamblul format din primele n-2 elemente;

etc.

procedure creare procedure sortare

for i= n/2 for i=n,2,-1

combin(i,n) a₁ a_i; combin(1,i-1)

end    end

Timpul total de lucru este de ordinul O(n log n)

Asa cum am mentionat chiar de la inceput, structura de arbore este implicita si este menita doar sa clarifice modul de lucru al algoritmului: calculele se refera doar la componentele vectorului.

Arbori de sortare

Un arbore de sortare este un arbore binar in care pentru orice varf informatia atasata varfului este mai mare decat informatiile varfurilor din subarborele stang si mai mica decat informatiile varfurilor din subarborele drept.

Observatie. Parcurgerea in inordine a unui arbore de cautare produce informatiile atasate varfurilor in ordine crescatoare.

Fie a=(a₁,a_n) un vector ce trebuie ordonat crescator. Conform observatiei de mai sus, este suficient sa cream un arbore de sortare in care informatiile varfului sa fie tocmai elementele vectorului. Pentru aceasta este suficient sa precizam modul in care prin adaugarea unei noi valori, sa obtinem tot un arbore de sortare.

Pentru exemplul considerat:

adaugarea valorii 6 trebuie sa conduca la crearea unui nou varf, cu informatia 6 si care este descendent stang al varfului cu informatia 7;

adaugarea valorii 16 trebuie sa conduca la crearea unui nou varf, cu informatia 16 si care este descendent drept al varfului cu informatia 15.

Presupunem ca un varf din arborele de sortare este o inregistrare sau obiect de tipul varf, ce contine campurile:

informatia info atasata varfului;

descendentul stang st si descendentul drept dr (lipsa acestora este marcata, ca de obicei, prin l

Crearea unui nou varf se face prin functia varf_nou care intoarce un nou varf:

function varf_nou(info)

creez un nou obiect/ o noua inregistrare x in care informatia este info, iar descendentul stang si cel drept sunt l

return x

end

Inserarea unei noi valori val (in arborele de radacina rad) se face prin apelul adaug(rad,val), unde functia adaug intoarce o inregistrare si are forma:

function adaug(x,val)

if x=l

then return varf_nou(val)

else if val<info(x)

then st(x) adaug(st(x),val)

else dr(x) adaug(dr(x),val)

end

Programul principal intreprinde urmatoarele actiuni:

citeste valorile ce trebuie ordonate si le insereaza in arbore;

parcurge in inordine arborele de sortare; vizitarea unui varf consta in tiparirea informatiei atasate.

Prezentam programul in Java:

class elem

elem(int ch)

elem adaug(elem x, int ch)

String parcurg(elem x)

class Arbsort

IO.writeln(Ob.parcurg(rad));

}

Arbori oarecare

Primele probleme care se pun sunt aceleasi ca pentru arborii binari: modalitatile de reprezentare si de parcurgere.

Exemplul 5. Consideram urmatorul arbore:

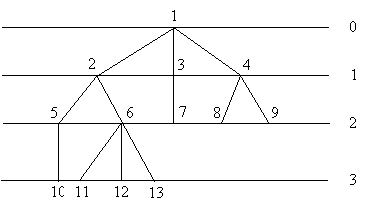
Se considera ca arborele este asezat pe niveluri si ca pentru fiecare varf exista o ordine intre descendentii sai.

Modul standard de reprezentare al unui arbore oarecare consta in a memora radacina, iar pentru fiecare varf i informatiile:

info(i) = informatia atasata varfului;

fiu(i) = primul varf dintre descendentii lui i

frate(i) = acel descendent al tatalui lui i, care urmeza imediat dupa i

Ca si pentru arborii binari, lipsa unei legaturi catre un varf este indicata prin l

Pentru arborele din Exemplul 5:

fiu    =(2,5,7,8,10,11,l l l l l l

frate =(l l l l l l l

O alta modalitate de reprezentare consta in a memora pentru fiecare varf tatal sau. Aceasta modalitate este incomoda pentru parcurgerea arborilor, dar se dovedeste utila in alte situatii, care vor fi prezentate in continuare.

In unele cazuri este util sa memoram pentru fiecare varf atat fiul si fratele sau, cat si tatal sau.

Parcurgerea in preordine

Se parcurg recursiv in ordine radacina si apoi subarborii care au drept radacina descendentii sai.

Pentru Exemplul 5:

Concret, executam apelul Apreord(rad) pentru procedura:

procedure Apreord(x)

if x=l

then

else vizit(x); Apreord(fiu(x)); Apreord(frate(x))

end

Ca aplicatie, sa presupunem ca informatiile atasate varfurilor sunt functii de diferite aritati (aritatea unei functii este numarul variabilelor de care depinde; o functie de aritate 0 este o constanta).

Pentru Exemplul 5, vectorul de aritate este:

aritate=(3,2,1,2,1,3,0,0,0,0,0,0,0)

Rezultatul al parcurgerii in preordine este o forma fara paranteze (dar la fel de consistenta) a scrierii expresiei functionale:

Aceasta forma se numeste forma poloneza directa.

Parcurgerea in postordine

Se parcurg recursiv in ordine subarborii radacinii si apoi radacina.

Pentru Exemplul 5:

Concret, executam apelul Apostord(rad) pentru procedura:

procedure Apostord(x)

if x=l

then

else y fiu(x);

while y<>l

Apostord(y); y frate(x)

vizit(x)

end

Pentru aplicatia anterioara, dorim sa calculam valoarea expresiei functionale, cunoscand valorile frunzelor. Evident, trebuie sa parcurgem arborele in postordine.

class varf

varf(int val)

void creare()

void creare(varf x)

IO.write('fratele lui ' + x.v + ' : '); d = IO.read();

if( !Double.isNaN(d) )

}

String pre(varf x)

void post(varf x)

IO.write(x.v + ' ');

}

}

class Arbori

}

Parcurgerea pe niveluri

Se parcurg varfurile in ordinea distantei lor fata de radacina, tinand cont de ordinea in care apar descendentii fiecarui varf. Pentru Exemplul 5:

Pentru implementare vom folosi o coada C, in care initial apare numai radacina. Atata timp cat coada este nevida, vom extrage primul element, il vom vizita si vom introduce in coada descendentii sai:

C ; C rad

while C

x C; vizit(x);

y fiu(x);

while y l

y T C; y frate(x)

end

Parcurgerea pe niveluri este in general utila atunci cand se cauta varful care este cel mai apropiat de radacina si care are o anumita proprietate/informatie.

Pentru a include in programul anterior si parcurgerea pe niveluri, putem proceda astfel:

in metoda main adaugam instructiunea:

IO.writeln('rNiveluri : ' +'t' + Ob.niveluri() );

in clasa varf adaugam clasa interna elem si metoda niveluri

class elem

}

String niveluri()

}

return s;

}