Metoda Divide et Impera - Timpul de calcul

Metoda Divide et Impera

I.1.1         Descrierea metodei

Metoda Divide et Impera ("Dezbina si Stapaneste") se aplica in problemele care pot fi impartite in mod repetat in doua sau mai multe sub-probleme de acelasi tip dar de dimensiuni mai mici [Divide], rezolvarea lor si combinarea solutiilor in scopul obtinerii solutiei problemei initiale [Impera].

Este o metoda clasica de programare, intalnita insa in viata de zi cu zi. Numele ei provine de la o manevra militara, prin care daca are loc o lupta intre doua armate intre care una este jumatate numeric din cea de-a doua, sansa ei este de a ataca pe rand diviziile armatei superioara numeric. In viata de zi cu zi, aplicam mereu metoda Divide et Impera atunci cand dorim sa "dam gata" masa de pranz: impartim mancarea in bucatele mici ("Divide"), suficient de mici pentru a fi inghitite una cate una ("Impera"). [Sfatul lui Abrams: "Cand mananci un elefant, nu-l inghiti pe tot deodata".]

Metoda Divide et Impera a fost deja utilizata in multe situatii: in algoritmii de parcurgere a arborilor binari, in algoritmul de cautare binara, in algoritmi de sortare (rapida, prin interclasare, prin distribuire) samd.

I.1.2         Exemplu - Problema turnurilor din Hanoi

Se considera trei tije: sursa 'a', intermediara 'b' si destinatie 'c' si n discuri de marimi diferite asezate in ordine descrescatoare (de la baza catre varf) a diametrelor lor pe tija sursa. Se cere ca, printr-un numar minim de mutari, sa se transfere toate discurile de pe tija sursa pe cea destinatie astfel ca niciodata sa nu se aseze un disc cu diametru mai mare peste unul cu diametru mai mic. La o mutare poate fi luat un singur disc aflat in varful unei tije.

Daca notam H(n,a,b,c) succesiunea de mutari care transfera n discuri de pe 'a' pe 'c' folosind 'b', atunci vom avea:

pentru n=1: H(1,a,b,c)=a->c

pentru n=2: H(2,a,b,c)= a b, a c, b c.

pentru n=3: H(3,a,b,c)= a c, a b, c b, a c, b a, b c, a c.

Grupam mutarile efectuate astfel:

H(3,a,b,c)= , a c, , care se mai poate scrie:

H(3,a,b,c)= H(2,a,c,b), a c, H(2,b,a,c)

Putem deduce astfel ca mutarea a n discuri de pe tija 'a' pe 'c', folosind tija intermediara 'b' este echivalenta cu:

mutarea a n-1 discuri din varful lui 'a' pe 'b' folosind 'c';

mutarea singurului disc ramas pe 'a', cel cu diametru mai mare decat cele deja ridicate, pe 'c';

mutarea celor n-1 discuri aflate acum pe 'b' pe 'c', folosind 'a'.

Sa consideram ca problema enuntata este de dimensiune n (numarul de discuri). Conform afirmatiei de mai sus, ea poate fi impartita in trei sub-probleme de acelasi tip, de dimensiuni n-1, 1 si respectiv n-1, astfel:

H(n,a,b,c)=H(n-1,a,c,b),a→c,H(n-1,b,a,c), cand n>1.

Evident, H(1,a,b,c)=a→c.

Rezolvarea sub-problemelor si combinarea rezultatelor vor duce la rezolvarea problemei turnurilor din Hanoi, folosind metoda Divide et Impera.

Algoritmul va fi:

In ceea ce priveste timpul de calcul asociat algoritmului de mai sus, daca notam T(n) timpul necesar mutarii a n discuri de pe o tija pe alta, atunci vom avea relatia de recurenta:

Se ajunge imediat ca: T(n)=2ⁿ-1, altfel spus, algoritmul este exponential.

Cum T(0)=0, expresia se reduce la o progresie geometrica de ratie 2 cu n termeni:

T(n)=2ⁿ-1.

Numarul mare de mutari necesare face ca un astfel de joc sa fi fost jucat de preotii din templul lui Brahma care considerau ca ultima mutare va aduce sfarsitul lumii. Ei utilizau 64 de discuri pentru care sunt necesare 2⁶⁴-1≈10¹⁸ mutari. Tinand cont ca un an are aproximativ 3*10⁷ secunde si ca o mutare este efectuata intr-o secunda, ar fi fost necesari 30 miliarde de ani pentru a termina jocul!

I.1.3         Timpul de calcul

Metoda Divide et Impera presupune rezolvarea unor sub-probleme de dimensiuni mai mici si combinarea solutiilor lor. In cazul cel mai defavorabil, sub-problemele sunt de dimensiune n-1 (asa cum se intampla in problema turnurilor din Hanoi).

Cea mai mare parte a aplicatiilor intalnite in practica presupun ca problema initiala, de dimensiune n, este descompusa in doua sub-probleme de dimensiuni egale n/2, situatie care corespunde principiului "balansarii", prin care sub-problemele sunt cat mai apropiate ca marime. Algoritmii de cautare binara, sortare prin interclasare samd. functioneaza dupa acest principiu al balansarii. Vom analiza timpul de calcul necesar in aceasta situatie.

Daca T(n) este timpul necesar rezolvarii problemei de dimensiune n, atunci fiecare dintre cele doua sub-probleme, care sunt similare celei initiale, doar cu alta dimensiune, necesita timpul T(n/2). Combinarea solutiilor sub-problemelor necesita un timp f(n). Rezolvarea unei sub-probleme de dimensiune e care nu mai poate fi descompusa necesita un timp constant t0. Asadar,

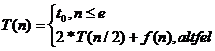
Forma functiei f(n) este esentiala in estimarea timpului total de calcul T(n). Astfel, daca f(n) este de complexitate O(n), adica este de forma

f(n)=c*n, unde c este constanta, atunci T(n)=O(n*log₂n).

Afirmatia de mai sus poate fi demonstrata foarte usor prin inductie: oricare ar fi n, fie cel mai mic k astfel ca n 2^k si cum T(n) este o functie crescatoare, avem: T(n) T(2^k)=2ⁱ*T(2^k-i)+c*2^k*i, pentru orice 1 i<k. In particular, pentru i=q, unde q este un numar natural astfel incat 2^q e, vom avea: T(n) = 2^k-q*T(2^q)+2^k*(k-q)*c 2^k*t₀+2^k*k*c = n*(t₀+c*log₂n) = O(n*log₂n), ceea ce este asimilat unui timp de calcul de ordin polinomial.

De exemplu, sa incercam sa evaluam timpul de calcul necesitat de strategia de sortare rapida, QuickSort, in situatia "optimista" in care pivotul ajunge pe pozitie centrala in vector. Avem ca:

Ne incadram in contextul situatiei de mai sus in care f(n)=n-1=O(n); atunci, conform propozitiei, algoritmul va fi de ordin polinomial O(n*log₂n).

I.1.4         Aplicatii

I.1.4.1   Turnurile din Hanoi

Enuntul problemei a fost prezentat mai sus.

Solutie:

Turnurile din Hanoi

#include<iostream.h>

void Hanoi(int n,char a,char b,char c)

void main()

Functia Hanoi poate fi implementata folosind numai doi parametri, astfel:

Turnurile din Hanoi

#include<iostream.h>

void Hanoi(int n,int a,int c)

void main()