Metoda Greedy

Metoda Greedy (greedy=lacom) este aplicabila problemelor de optim.

Consideram multimea finita A= si o proprietate p definita pe multimea submultimilor lui A

p:P(A) cu

O submultime S A se numeste solutie daca p(S)=1

Dintre solutii aleg una care optimizeaza o functie p:P(A) R data.

Metoda urmareste evitarea parcurgerii tuturor submultimilor (ceea ce ar necesita un timp de calcul exponential), mergandu-se 'direct' spre solutia optima. Nu este insa garantata obtinerea unei solutii optime; de aceea aplicarea metodei Greedy trebuie insotita neaparat de o demonstratie.

Distingem doua variante generale de aplicare a metodei Greedy:

Observatii

in algoritm nu apare functia f

timpul de calcul este liniar (exceptand prelucrarile efectuate de procedurile prel si alege

dificultatea consta in a concepe procedurile alege, respectiv prel, in care este 'ascunsa' functia f

Exemplul 1. Se considera multimea de valori reale A=. Se cauta submultimea a carei suma a elementelor este maxima.

Vom parcurge multimea si vom selecta numai elementele pozitive.

k

for i=1,n

if a_i>0

then k k+1; s_k a_i

write(s)

Exemplul 2. Caut cel mai lung sir strict crescator format cu elemente din multimea

Incepem prin a ordona crescator elementele multimii (corespunzator procedurii prel). Apoi eliminam dublurile.

Astfel, daca in urma ordonarii a rezultat a=(1,1,2,3,4,4,5,6,7,8,8}, vom obtine succesiv:

s=(1,2,3,4,5,6,7,8)

(Contra)exemplul 3. Fie multimea A= cu elemente pozitive. Caut submultimea de suma maxima, dar cel mult egala cu M dat.

Daca procedez ca in exemplul 1, pentru A=(6,3,4,2) si M=7 obtin . Dar solutia optima este cu suma egala cu 7.

Continuam cu prezentarea unor exemple clasice.

Memorarea textelor pe banda

Textele cu lungimile L(1),,L(n) urmeaza a fi asezate pe o banda. Pentru a citi textul de pe pozitia k, trebuie citite textele de pe pozitiile 1,2,,k (conform specificului accesului secvential pe banda).

O solutie inseamna o permutare pIS_n

Pentru o astfel de permutare (ordine de asezare a textelor pe banda), timpul pentru a citi textul de pe pozitie k este: T_p(k)=L(p₁)++L(p_k). Presupunand textele egal probabile, trebuie minimizata valoarea .

Sa observam ca functia T se mai poate scrie:

(textul de pe pozitia k este citit daca vrem sa citim unul dintre textele de pe pozitiile k,,n

Conform strategiei Greedy, incepem prin a ordona crescator vectorul L. Rezulta ca in continuare L(i)<L(j), i<j

Demonstram ca in acest mod am obtinut modalitatea optima, adica permutarea identica minimizeaza functia de cost T

Fie pIS_n optima, adica p minimizeaza functia T. Daca p este diferita de permutarea identica T i<j cu L(p_i)>L(p_j)

Consideram permutarea p' in care am interschimbat elementele de pe pozitiile i si j

Atunci n[T(p)-T(p')] = (n-i+1)L(p_i) + (n-j+1)L(p_j) -

- (n-i+1)L(p_j) - (n-j+1)L(p_i) =

= (j-i)L(p_i)+(i-j)L(p_j) =

= (j-i)[L(p_i)-L(p_j)]>0, ambii factori fiind pozitivi.

Rezulta ca T(p')<T(p). Contradictie.

Problema continua a rucsacului

Se considera un rucsac de capacitate (greutate) maxima G si n obiecte caracterizate prin:

greutatile lor g₁,,g_n

castigurile c₁,,c_n obtinute la incarcarea lor in totalitate in rucsac.

Din fiecare obiect poate fi incarcata orice fractiune a sa.

Se cere o modalitate de incarcare de (fractiuni de) obiecte in rucsac, astfel incat castigul total sa fie maxim.

Prin solutie intelegem un vector x=(x₁,.,x_n) cu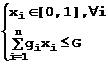

O solutie optima este solutie care maximizeaza functia .

Daca suma greutatilor obiectelor este mai mica decat G, atunci incarc toate obiectele: x=(1,,1). De aceea presupunem in continuare ca g₁++g_n>G

Conform strategiei Greedy, ordonez obiectele descrescator dupa castigul la unitatea de greutate, deci lucram in situatia:

(*)

Algoritmul consta in incarcarea in aceasta ordine a obiectelor, atata timp cat nu se depaseste greutatea G (ultimul obiect pote fi eventual incarcat partial):

G1 G

for i=1,n

if g_i G1 then x_i 1; G1 G1-g_i

else x_i G1/g_i;

for j=i+1,n

x_j

stop

write(x)

Am obtinut deci x=(1,,1,x_j,0,,0) cu x_jI

Aratam ca solutia astfel obtinuta este optima.

Fie y solutia optima: y=(,y_k,) cu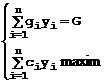

Daca y x, fie k prima pozitie pe care y_k x_k

Observatii:

k j: pentru k>j se depaseste G

y_k<x_k

pentru k<j: evident, deoarece x_k=1

pentru k=j: daca y_k>x_k se depaseste G

Consideram solutia: y'=(y₁,,y_k-1,x_k,ay_k+1,, ay_n) cu a<1 (primele k-1 componente coincid cu cele din x). Pastram greutatea totala G, deci:

g_kx_k+a(g_k+1y_k+1++g_ny_n)=g_ky_k+g_k+1y_k+1++g_ny_n. Rezulta:

g_k(x_k-y_k)=(1-a)(g_k+1y_k+1+.+g_ny_n)    (**)

Compar performanta lui y' cu cea a lui y

f(y')-f(y) = c_kx_k +ac_k+1y_k+1 ++ ac_ny_n - (c_ky_k+c_k+1y_k+1 ++c_ny_n) =

= c_k(x_k-y_k) + (a-1)(c_k+1y_k+1++c_ny_n) =

= c_k/g_k[g_k(x_k-y_k)+(a-1)(g_k/c_kc_k+1y_k+1++g_k/c_kc_ny_n)]

Dar a-1<0 si g_k/c_k g_s/c_s s>k

Atunci f(y')-f(y)>c_k/g_k [g_k(x_k-y_k)+(a-1)(g_k+1y_k+1++g_ny_n)]=0, deci f(y')>f(y). Contradictie.

Problema discreta a rucsacului difera de cea continua prin faptul ca fiecare obiect poate fi incarcat numai in intregime in rucsac.

Sa observam ca aplicarea metodei Greedy esueaza in acest caz. Intr-adevar, aplicarea ei pentru:

G=5, n=3 si g=(4,3,2), c=(6,4,2.5)

are ca rezultat incarcarea primul obiect; castigul obtinut este 6. Dar incarcarea ultimelor doua obiecte conduce la castigul superior 6.5.

Problema arborelui partial de cost minim.

Fie G=(V,M) un graf neorientat cu muchiile etichetate cu costuri strict pozitive. Se cere determinarea unui graf partial de cost minim.

Ca exemplificare, sa consideram n orase initial nelegate intre ele. Pentru fiecare doua orase se cunoaste costul conectarii lor directe (consideram acest cost egal cu daca nu este posibila conectarea lor). Constructorul trebuie sa conecteze orasele astfel incat din oricare oras sa se poata ajunge in oricare altul. Ce legaturi directe trebuie sa aleaga constructorul astfel incat costul total al lucrarii sa fie minim?

Este evident ca graful partial cautat este un arbore (daca ar exista un ciclu, am putea indeparta o muchie din el, cu pastrarea conexitatii si micsorarea costului total).

Vom aplica metoda Greedy: adaug mereu o muchie de cost minim dintre cele nealese si care nu formeaza un ciclu cu precedentele muchii alese.

Acest algoritm poarta numele de algoritmul lui Kruskal.

Ca de obicei, fie |V|=n |M|=m. Vor fi alese deci n-1 muchii.

Construim o matrice mat cu m linii si n coloane. Pe fiecare linie apar extremitatile i si j ale unei muchii, precum si costul acestei muchii.

Incepem prin a ordona liniile matricii crescator dupa ultima coloana (a costurilor muchiilor).

Exemplu. Consideram graful de mai jos si matricea mat atasata.

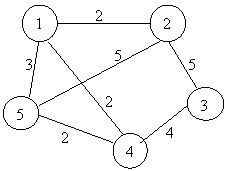
Conform algoritmului lui Kruskal, vor fi alese in ordine muchiile:

cu costul total egal cu 10. Muchia (1,5) nu a fost aleasa deoarece formeaza cu precedentele un ciclu.

Dificultatea principala consta in verificarea faptului ca o muchie formeaza sau nu cu precedentele un ciclu. Plecand de la observatia ca orice solutie partiala este o padure, vom asocia fiecarui varf i un reprezentant r_i care identifica componenta conexa (arborele) din care face parte varful in solutia partiala. Atunci:

o muchie (i,j) va forma un ciclu cu precedentele r_i=r_j

la alegerea (adaugarea) unei muchii (i,j) vom pune r_k r_j pentru orice varf k cu r_k=r_i (unim doi arbori, deci varfurile noului arbore trebuie sa aiba acelasi reprezentant).

In algoritmul care urmeaza metoda descrisa, l este numarul liniei curente din matricea mat nm este numarul de muchii alese, iar cost este costul muchiilor alese

r_i i, i=1,n

l 1; nm 0; cost

while l m & nm<n-1

i1 mat(l,1); i2 mat(l,2)

r1 r_i1; r2 r_i2

if r1 r2

then nm nm+1; cost cost+mat(l,3);

write(i1,i2)

for k=1,n

if r_k=r2 then r_k r1

l l+1

if nm<n-1 then write('Graf neconex')

else write('Graf conex. Costul=',cost)

Demonstram in continuare corectitudinea algoritmului lui Kruskal.

Fie G=(V,M) un graf conex.

P M se numeste multime promitatoare de muchii daca nu contine cicluri si poate fi extinsa la un arbore partial P de cost minim. In particular P nu contine cicluri (este o padure).

Propozitie. La fiecare pas din algoritmul lui Kruskal muchiile alese formeaza o multime promitatoare P. In plus, muchiile din PP nu au costuri mai mici decat cele din P

Fie P multimea promitatoare a muchiilor selectate la primii k pasi si fie m muchia considerata la pasul k+1. Deosebim situatiile:

daca m inchide un ciclu in P, ea este ignorata. P si P raman aceleasi.

daca m nu inchide un ciclu in P si face parte din P, noile instante ale lui P si P sunt P si P

daca m nu inchide un ciclu in P si nu face parte din P, atunci P are un ciclu. In el exista, in afara de m, o muchie m' din PP, deci de cost mai mare sau egal decat cel al lui m. Fie P'=P P' este tot un arbore partial de cost minim. Noile instante ale lui P si P sunt P si P'

In final, o multime promitatoare cu n-1 muchii este chiar un arbore partial de cost minim.

Observatie. Tot o ilustrare a metodei Greedy pentru problema enuntata o constituie algoritmul lui Prim, care consta in urmatoarele:

se incepe prin selectarea unui varf;

la fiecare pas aleg o muchie (i,j) de lungime minima cu i selectat, dar j neselectat.

De aceasta data, la fiecare pas se obtine un arbore. Propunem ca exercitiu demonstrarea faptului ca dupa n-1 pasi se obtine un arbore partial de cost minim.