Retele neuronale

I.1          Neuronul artificial

Retelele neuronale reprezinta o preocupare relativ noua a cercetatorilor din lumea intreaga, fiind o ramura a domeniului inteligentei artificiale. Ele au aparut din necesitatea de a realiza sisteme automate capabile sa efectueze functii pe care omul le indeplineste cu mare usurinta, cum ar fi gandirea, vorbirea, mersul, recunoasterea obiectelor samd.

Una dintre primele aplicatii ale retelelor neuronale a fost recunoasterea caracterelor, aplicatie ce a fost integrata intr-un sistem automat de triere a scrisorilor. Astfel, pe baza codului postal recunoscut, o scrisoare poate fi triata intr-o fractiune de secunda.

Ulterior, aplicatiile retelelor neuronale au fost din ce in ce mai variate, cuprinzand ariile recunoasterii si sintezei semnalului vocal, ale formelor samd., toate acestea fiind posibile prin construirea unui sistem capabil sa invete si sa exploateze ceea ce a invatat.

Retelele neuronale au ca punct de inspiratie sistemul nervos. De aceea, pentru a intelege retelele neuronale, sa facem mai intai o foarte scurta incursiune in sistemul nervos. Sistemul nervos este o retea de neuroni interconectati intre ei. Astfel neuronii reprezinta unitatea de baza a sistemului nervos. Un neuron este o celula care prezinta mai multe dendrite si un axon, acestea fiind caile de legatura cu alti neuroni. Dendritele conduc impulsurile nervoase primite catre neuron, excitandu-l. Acesta transforma intr-o anumita maniera impulsul primit si genereaza un alt impuls pe care il trimite, pe calea axonului, catre alti neuroni. Axonul este unic, insa el se ramifica, putand constitui cale de intrare pentru mai multi neuroni. Dendritele nu reprezinta numai o cale de transfer a impulsului nervos catre neuron, ele pondereaza (independent de celelalte) semnalul primit.

Similar, retelele neuronale au fost gandite ca o retea de noduri (neuroni artificiali), ce au mai multe intrari si o singura iesire, dar care poate fi conectata la intrarea mai multor noduri. Astfel, neuronul artificial primeste mai multe semnale de intrare, le pondereaza corespunzator intrarii pe care au venit, le prelucreaza (le aplica a anumita functie, numita functie de activare) si genereaza o iesire.

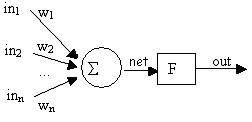
Fig. VI . Neuronul artificial

Mai sus este reprezentat schematic un neuron artificial, unde in₁, in₂, , in_n reprezinta semnalele primite, w₁, w₂, , w_n sunt ponderile aplicate de catre fiecare intrare in neuron, apoi semnalele ponderate sunt insumate, obtinandu-se un singur impuls ce va fi prelucrat de catre neuronul artificial cu o functie F, numita functie de activare, de unde rezulta iesirea out. Asa cum vom vedea mai tarziu, performantele unei retele neuronale depind in mod direct de modul in care neuronul prelucreaza semnele de intrare, si anume de functia de activare F, practic aceasta controleaza rapiditatea cu care "invata" reteaua neuronala.

Asadar,

si

.

In practica, alegerea functiei de activare se face prin experimente, neexistand la ora actuala nici o teorie care sa determine aceasta alegere. In general se aleg functii derivabile (din motive pe care le vom justifica mai jos) care restrang domeniul de variatie al iesirii neuronului. Una dintre cele mai uzuale functii de activare este:

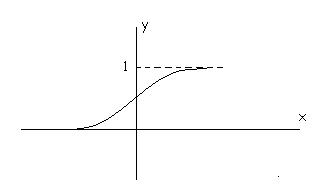
Fig. VI . Functia de activare

care restrange domeniul valorilor iesirii la intervalul (0,1).

I.2          Sisteme de invatare-testare

Retelele neuronale sunt sisteme de inteligenta artificiala capabile sa invete, in urma antrenarii lor pe un set de exemple de care dispun, numit set de antrenare (sau formare), ele pot apoi generaliza    si testa ceea ce au invatat. Din acest motiv ele mai sunt numite sisteme de invatare-testare. Invatarea (sau antrenarea) retelei este cea mai importanta etapa, de reusita ei depinzand performantele acesteia. Cunostintele retelei sunt "inmagazinate" in ponderile neuronilor artificiali care o compun.

In functie de modul in care sunt interconectati neuronii artificiali exista mai multe tipologii de retele neuronale. In aceasta sectiune ne vom referi la retelele neuronale cu reactie inainte (feedforward) total conectate. Acestea sunt caracterizate de faptul ca neuronii artificiali sunt asezati pe mai multe niveluri si iesirea fiecarui neuron de pe un nivel este conectata la intrarile tuturor neuronilor de pe nivelul imediat urmator. Cea mai simpla configuratie este cea cu un singur nivel, la care ne vom referi in continuare:

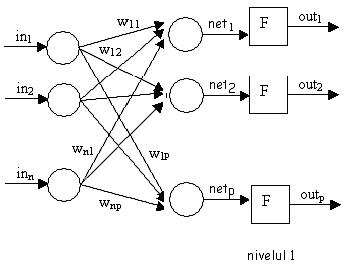
Fig. VI‑ . Retea neuronala feedforward cu un singur nivel

Reteaua din figura are n intrari, un singur nivel cu functia de activare F, p iesiri si ponderile w_ij, i=1..n, j=1..p.

Pentru a intelege mai bine functionarea unei retele neuronale sa consideram un exemplu. Sa presupunem ca dorim sa construim un sistem capabil sa recunoasca cifre scrise de mana (OCR = Optical Character Recognition). Vom considera in acest sens cifrele reprezentate sub forma de matrice binare unde fiecare celula a matricei este 1 daca acopera cifra sau 0 in caz contrar.

Fig. VI . Reprezentarea binara a cifrei 3

In acest caz reteaua neuronala va avea n=24 intrari (corespunzator numarului de celule ale matricei), fiecare intrare avand aici o valoare binara, si p=10 iesiri (corespunzator numarului de cifre posibile, de la 0 la 9). In exemplul de mai sus, pentru cifra 3 considerata avem intrarea in retea:

pentru care iesirea se poate reprezenta ca un vector caracteristic:

0001000000

corespunzator cifrei 3.

Pentru invatarea retelei se considera un set de antrenare compus din obiecte cunoscute: forma care trebuie invatata alaturi de semnificatia ei (iesirea pe care ar trebui sa o produca reteaua sau rezultatul asteptat). O pereche de antrenament ar putea fi:

0001000000]

conform exemplului anterior.

Mecanismul de functionare este urmatorul: fiecare pereche din setul de antrenament este "trecuta" (propagata) prin retea -pasul forward- generand o iesire, aceasta se compara cu rezultatul asteptat si in functie de diferenta lor (eroarea obtinuta), se ajusteaza corespunzator ponderile w_ij ale retelei -pasul backward- printr-un procedeu stabilit aprioric care tinde sa minimizeze eroarea. Initial, ponderile w_ij au valori arbitrare mici. Se reia procedeul pentru toate perechile din setul de antrenament pana cand eroarea obtinuta este acceptabila (sub un anumit prag). Antrenarea repetata pe setul de formare este necesara pentru a evita pe cat posibil fenomenul de "uitare": atunci cand setul de formare este mare, invatand ultimele perechi, reteaua le poate uita pe primele, procedand similar creierului nostru atunci cand incercam intr-un mod neorganizat sa inmagazinam in scurt timp un volum mare de date.

Algoritmul de functionare al unei retele feedforward total conectata cu un singur nivel este urmatorul:

Ajustarea ponderilor se poate face in mai multe moduri. De exemplu se poate utiliza metoda gradientului, prin care ponderile care minimizeaza functia e² (privita ca functie de n*p argumente (w_ij)_{i=1..n,j=1..p}) se obtin din aproape in aproape adaugand valorii curente a lui w_ij, la fiecare iteratie, valoarea derivatei partiale a functiei e² fata de w_ij ponderata cu o constanta numerica mica a. Eroarea patratica este:

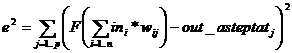
De aici rezulta ca:

, pentru i=1..n,j=1..p oarecare dar fixate (in suma de patrate toti termenii sunt constanti in raport cu w_ij, cu exceptia unuia singur, care are indicii i si j cei fixati).

Daca utilizam ca functie de activare , pentru care avem ca:

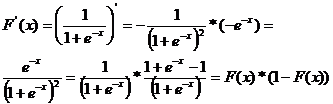
va rezulta:

Notand , avem ca:

In acest caz, pasul B2 din algoritm devine:

Asa cum se observa, retelele neuronale necesita algoritmi simpli, ce nu se modifica de la o aplicatie la alta, asa cum se intampla in cazul algoritmilor uzuali; ceea ce diferentiaza o problema de alta este setul de formare cu care este antrenata reteaua. Altfel spus, odata ce am realizat un sistem de recunoastere a cifrelor scrise de mana, il putem refolosi mai departe pentru a recunoaste litere, sau diverse alte forme, totul este sa ii furnizam sistemului setul de antrenament adecvat. Valorile ponderilor obtinute dupa antrenare depind de setul de formare si nu pot fi refolosite in alte aplicatii.

Atat numarul perechilor din setul de antrenament, cat si forma acestora depind de complexitatea problemei, nu exista o teorie referitoare la alegerea acestora, insa este de la sine inteles faptul ca cu cat setul de formare este mai cuprinzator, cu atat precizia raspunsului retelei va fi mai buna.

Asadar, initial ponderile w_ij aveau valori arbitrare mici. Dupa antrenarea retelei pe baza setului de antrenament, ponderile w_ij vor "ingloba" cunostintele retelei. Aceasta va fi acum capabila sa recunoasca forme de intrare care nu fac parte din setul de antrenament, ea este capabila astfel de predictie. Cu alte cuvinte, pentru un vector de intrare (in_i)_i=1..n necunoscut de retea se va obtine prin propagare inainte (pasul forward) un vector de iesire (out_j)_j=1..p pe baza caruia se va decide din ce clasa face parte forma de intrare considerata: se va alege clasa j "cea mai probabila", pentru care componenta out_j a vectorului de iesire este maxima.

I.3          Performantele unui sistem de invatare-testare

Performantele unui sistem de invatare-testare pot fi evaluate astfel:

capacitatea de recunoastere - este data de abilitatea de a recunoaste forme din setul de antrenament; viteza de formare reprezinta procentul de forme recunoscute corect;

convergenta - este data de viteza cu care algoritmul utilizat in faza de formare duce la o viteza de recunoastere de 100%;

siguranta - este data de capacitatea de a clasifica corect formele din setul de formare usor distorsionate;

predictia - este capacitatea de a clasifica corect forme ce nu apartin setului de formare, deci pentru care reteaua nu a fost antrenata.

I.4          Aplicatie-recunoasterea cifrelor scrise de mana

In aceasta sectiune va fi implementat in limbajul C++ un sistem de invatare-testare capabil sa recunoasca cifre scrise de mana. Pentru simplitate, am inclus in setul de antrenament numai cifrele 0, 1, 2 si 3. Fiecare cifra este prezenta in doua variante. Testarea sistemului a fost facuta cu doua cifre: o cifra oarecare din setul de antrenament si o cifra ce nu face parte din setul de antrenament. Pentru o mai buna intelegere, dupa propagarea in retea a fiecarei cifre de test a fost afisat vectorul de ponderi; se va observa cum intervine in compozitia acestuia alegerea erorii minime acceptata (Eps). Lasam cititorul sa evalueze performantele retelei.

Recunoasterea cifrelor scrise de mana

#include<iostream.h>

#include<math.h>

#include<stdlib.h>

#define N 24

#define P 4//cifrele 0, 1 2 si 3

#define a 0.35

#define Eps 1e-4

struct Perecheperechi[]=

,,},

,,},

,,},

,,},

,,},

,,},

,,},

double out[P],net[P],w[N][P],v[P];

double F(double x)

void Forward(int in[N])

double Backward(int in[N], int out_asteptat[P])

//ajustam ponderile

for(int i=0;i<N;i++)

for(j=0;j<P;j++)

w[i][j]+=a*v[j]*in[i];

return err;

void OCR(int nr_perechi)

while(err>Eps);

void RaspunsRetea(int in[N])

//raspuns retea:

int prob_max=0;

cout<<endl<<'out=[';

for(int j=0;j<P;j++)

cout<<']-->Raspuns retea: cifra '<<prob_max<<endl<<endl;

main();

Forward(cifra_test);

RaspunsRetea(cifra_test);

return 0;

Programul va genera iesirea:

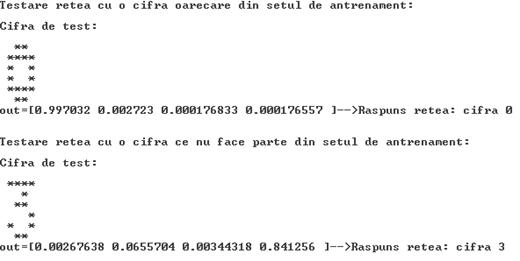
Asa cum s-a precizat mai sus, sistemul realizat poate fi utilizat cu succes pentru recunoasterea oricarui set de forme: cifrele de la 0 la 9, litere scrise de mana, forme geometrice, obiecte care ne inconjoara samd.