Analiza statistica a datelor in raport cu doua variabile

Analiza statistica a datelor in raport cu doua variabile
1. Cazul a doua variabile nominale

Tabele de repartitie bidimensionale pentru a reda distributia esantionului in raport cu 2 variabile se procedeaza astfel: Analyze - Descriptive Statistics - Crosstabs:

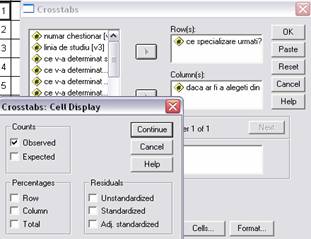
In fereastra Cells putem opta pentru optiunea Counts Observed, caz in care ne va afisa tabelul bidimensional cu ajutorul frecventelor absolute, sau alegand optiunea Percentages, vom obtine distributia esantionului in raport cu cele 2 variabile cu ajutorul frecventelor relative.

Interpretare: tabelul reda distributia studentilor din esantion in raport cu cele doua variabile, fiind construit cu ajutorul frecventelor absolute. Ultima coloana si ultimul rand din tabelul de frecvente corespund repartitiilor marginale.

Ex: doar 2 din cei 24 de studenti chestionati de la sectia de marketing ar alege alta specializare.

Aceeasi distributie a esantionului in raport cu cele doua variabile poate fii redata si cu ajutorul frecventelor relative. Se observa ca 21,3% din totalul studentilor ar alege alta sectie, un procent insemnat avand cei de la sectia management (5,9%).

Grafice adecvate in acest caz sunt diagramele prin coloane.

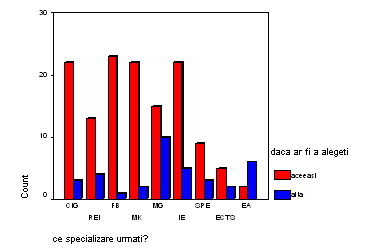
Analiza asocierii dintre cele doua variabile presupune in prima etapa verificarea existentei legaturii dintre cele doua variabile cu ajutorul testului χsi apoi interpretarea coeficientului de contingenta pentru a analiza gradul de asociere dintre variabile. Din meniul Analyze - Descriptive Statistics - Crosstabs se aleg cele doua variabile si in fereastra Statistics se selecteaza parametrii doriti.

Se formuleaza ipotezele referitoare la existenta legaturii:

H: χ= 0 ( nu exista legatura )

H: χ≠ 0

Interpretare: putem afirma cu o probabilitate de 95% ( Sig.< 0,05 ) ca intre cele doua variabile exista legatura.

Valoarea coeficientului de contingenta este de 0,373, fiind semnificativ diferit de 0, deci legatura dintre variabile este de intensitate medie.

2. Cazul a doua variabile ordinale

Tabele de repartitie bidimensionale si in acest caz prezinta importanta repartitia esantionului in raport cu cele variabile atat sub forma frecventelor absolute, cat si relative. Aceasta prezentare a datelor presupune urmatorii pasi: Analyze - Descriptive Statistics - Crosstabs, in fereastra Cells alegand si optiunea Percentages. Cele doua tipuri de frecvente, absolute si relative, se pot prezenta in acelasi tabel de repartitie.

Grafice informatii privind repartitia esantionului in raport cu doua variabile ordinale sunt disponibile si din vizualizarea graficului adecvat - diagrama prin benzi. Modul de obtinere a acestuia este: Graphs - Bar - Clustered.

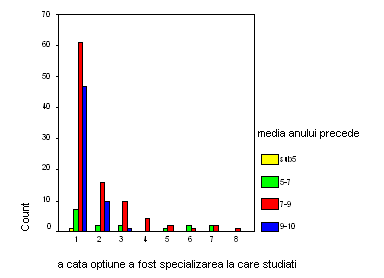
Analiza corelatiei se realizeaza cu ajutorul coeficientului lui Kendall, astfel: Analyze - Descriptive Statistics - Crosstabs, selectand in fereastra Statistics acest coeficient.

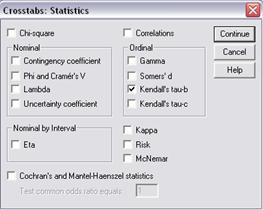
Valoarea coeficientului lui Kendall de - 0,252 indica faptul ca intre media anului precedent si ordinea repartizarii pe sectii a studentilor exista o legatura inversa, de intensitate slaba. Cu cat studentii au o medie mai mare, cu atat au sansa de a fi repartizati in sectia pentru care si-au exprimat prima preferinta.Valoarea coeficientului este semnificativ diferita de 0 cu o probabilitate de 95% ( Sig.= 0,000 < 0,05 ).

3. Cazul a doua variabile cantitative

Tabele de repartitie bidimensionale se parcurg aceleasi etape ca si mai sus;

Grafice pentru a reda repartitia esantionului folosim in acest caz norul statistic. Demersul pentru construirea acestuia este: Graphs - Scatter - Simple. Construirea norului statistic constituie prima etapa in analiza legaturii dintre doua variabile numerice. In functie de pozitiile punctelor norului putem formula de asemenea ipoteze cu privire la forma functiei care explica legatura dintre variabile.

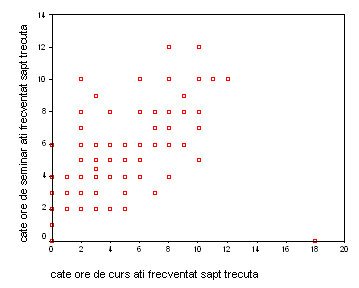
Se observa in distributia punctelor o valoare extrema ( 18 ore curs ); se recomanda ca valorile extreme sa fie inlaturate inaintea aplicarii testelor statistice pentru a nu influenta calitatea rezultatelor.

Analiza corelatiei - presupune calculul coeficientului lui Pearson, utilizand meniul Analyze - Correlate - Bivariate.

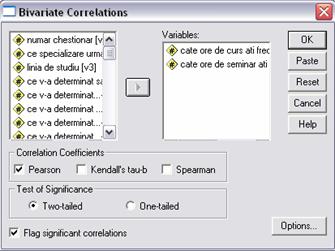Vom analiza legatura dintre numarul de ore de curs si cele de seminar frecventate de studenti intr-o saptamana. Coeficientul lui Pearson ne ofera informatii atat despre sensul legaturii, cat si despre intensitatea legaturii.

Se obtine matricea de corelatie, valorile fiind distribuite simetric fata de diagonala principala. Valoarea coeficientului lui Pearson este de 0,665, ceea ce sugereaza ca intre variabile exista o corelatie directa, de intensitate medie.

Valoarea acestui coeficient este semnificativ diferita de 0, ipoteza existentei legaturii fiind acceptata cu o probabilitate de 95% ( Sig.< 0,05 ).

Daca analizam din nou corelatia dintre cele doua variabile, dar dupa indepartarea valorilor extreme din esantion, rezultatele vor fi mai concludente:

Correlations

Se observa ca intensitatea legaturii dupa inlaturarea valorilor extreme se modifica, legatura dintre cele doua variabile fiind mai bine pusa in evidenta.

4. Testarea egalitatii a doua medii ( esantioane independente ) - este un test parametric care verifica daca mediile a doua grupe sunt egale. In SPSS presupune urmatorul demers: Analyze - Compare Means - Independent Samples T Test.   

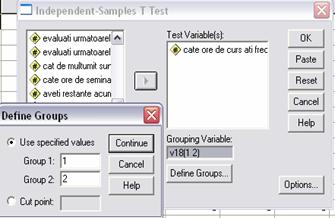De exemplu, dorim sa testam daca, la nivelul esantionului observat, numarul mediu de ore de curs frecventate de studentii din anul 4 este diferit de numarul mediu de ore de curs frecventate de studentii din anul 5.

Variabila de grupare va fi in acest caz anul de studiu, in definirea grupelor tinand cont de codificarile facute pentru starile acesteia ( 1 - anul 4, 2 - anul 5 ).

Ipoteza privind egalitatea mediilor se formuleaza astfel:

H: =

H: ≠

Dorim sa verificam daca numarul mediu de ore de curs frecventate de studentii din anul 4 ( 5,29≈5 ), difera semnificativ de 3,65≈4 (numarul mediu de ore de curs frecventate de studentii din anul 5 ).

Constructia testului pentru compararea mediilor a doua esantioane presupune testarea in prealabil a egalitatii variantelor la nivelul celor doua grupe. Statistica t se calculeaza diferit dupa cum dispersiile sunt egale sau nu la nivelul celor doua grupe. Ca urmare, formulam ipoteza nula si alternativa referitoare la egalitatea dispersiilor:H: σ= σ iar H: σ≠ σ

Interpretare: probabilitatea de acceptare a ipotezei nule in cazul egalitatii variantelor este de 0,402 ( > 0,05 ), variantele la nivelul celor doua grupe sunt egale. Pentru a verifica egalitatea mediilor folosim statistica t corespunzatoare cazului in care dispersiile sunt egale. In acest caz, testul t este egal cu 1,935, cu 168 grade de libertate si un nivel de semnificatie de 0,055 ( Sig.> 0,05 ), ceea ce arata ca nu se poate trage concluzia ca cele doua medii difera semnificat

5. Testarea legaturii dintre doua variabile - dorim sa verificam daca modificarea variabilei dependente Y este rezultatul influentei variabilei explicative X. Pentru a testa existenta legaturii procedam astfel: Analyze - Compare Means - One Way Anova. ANOVA este un procedeu de analiza a unei variabile numerice sub influenta unei variabile de grupare care prezinta mai multe stari.

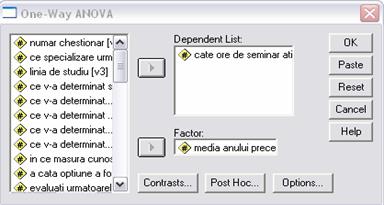De exemplu dorim sa verificam daca exista legatura intre numarul de ore de curs frecventate si media anuala.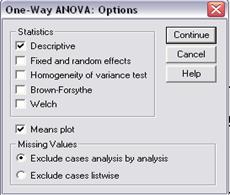

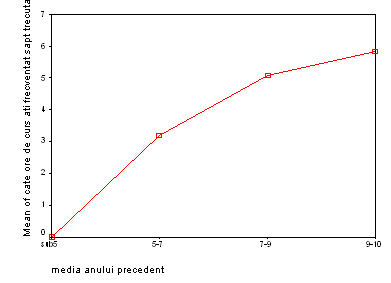
In meniul Options avem posibilitatea selectarii graficului pentru a formula ipoteze cu privire la forma legaturii dintre cele doua variabile.

Cu cat mediile grupelor au valori mai diferite intre ele, cu atat variatia dintre grupe este mai mare; cu cat variatia in cadrul grupelor este mai mica, cu atat statistica F este mai mare (F = media variantei dintre grupe /media variantei din cadrul grupei ) si numarul orelor de curs frecventate variaza mai mult in raport cu media anuala.

Se formuleaza ipoteza nula H: F = 0, adica dispersia dintre grupe este nula si deci grupele nu sunt diferite intre ele, adica media anuala nu influenteaza numarul orelor de curs frecventate de studenti. Deoarece probabilitatea de a gresi cand respingem ipoteza este 0,016< 0,05, rezulta ca ipoteza nula se respinge, adica media influenteaza frecventa la cursuri,. In cadrul fiecarui interval al mediei anului precedent, studentii sunt relativ omogeni din punct de vedere al frecventarii cursurilor, media anului precedent fiind un criteriu semnificativ de segmentare.