TRANSFORMARI CONSERVATIVE IN BAZE DE DATE

Transformarea de proiectie-unire ( pe scurt PJ-transformare ) a unei relatii r(R) determinata de schema bazei de date R AR₁,R₂,.,R_p} este utilizata pentru caracterizarea descompunerilor conservative ( fara pierderi de informatii ) .

Descompuneri fara pierderi de informatii

Fie o schema R si o descompunere a lui R in schemele R₁,R₂,,R_p astfel ca R=R₁ÈR₂È ÈR_p si F o multime de F-dependente pe R. Descompunerea este fara pierderi (loss join descompozition) in raport cu F daca orice relatie r de schema R care satisface F atunci

r=_R1(r)_R2(r) ._Rp(r).

Teorema 1 (Criteriul de descompunere fara pierderi) Fie schema de relatie R, descompunerea aR₁,R₂s si F o multime de F-dependente. Daca F implica una din urmatoarele F-dependente:

i)           R₁ R₂ R₁tR₂

ii)         R₁ R₂ R₂tR₁

iii)      R₁ R₂ R₁

iv)        R₁ R₂ R₂

atunci orice relatie r(R) care satisface F se descompune fara pierderi de informatie, adica r=p_R1(r)p_R2(r).

Demonstratie. i) Fie relatia r care satisface F, este suficient sa aratam ca r include p_R1(r)p_R2(r). Fie tuplul tIp_R1(r)p_R2(r) atunci exista tuplurile t₁,t₂Ir astfel incat t₁(R₁)=t(R₁) si t₂(R₂)=t(R₂) din care rezulta ca t₁(R₁ R₂)=t₂(R₁ R₂). Deoarece r satisface F rezulta t₂(R₂)=t(R₂), t₂(R₁tR₂)=t₁(R₁tR₂)=t(R₁tR₂), din care rezulta t(R₁ÈR₂)=t₂(R₁ÈR₂) adica t=t₂ deci tIr.

Relatiile ii),iii) si iv) se demonstreaza analog.

Transformari conservative

Criteriul de conservare a relatiei prin descompunere este dat de relatia :

r=_R1(r)_R2(r) _Rp(r) .

In continuare se prezinta o metoda pe baza careia se decide daca o dependenta ( F sau J ) este implicata de o multime de dependente ( F- si / sau J-dependente ) .

Definitia 1. Fie R AR₁,R₂,.,R_p} o multime de scheme de relatii si R R₁R₂.R_p . Se numeste transformare de proiectie-unire definita de R , functia de relatie de schema R notata data de relatia : (r) _R1(r)_R2(r) _Rp(r).

Exemplul 1 Fie R AABC , BC , ADE } si R ABCDE . Se considera relatia

r(R) din figura 1 . Rezultatul aplicarii transformarii m_R lui r este relatia s(R) .

r ( A B C D E ) s ( A B C D E )

3 1 5 7 8 3 1 5 7 8

3 4 5 2 8 3 4 5 2 8

3 4 5 2 9 3 4 5 2 9

3 1 5 2 9 3 1 5 2 9

3 1 5 2 9

Figura 1 Figura 2

Definitia 2. Fie R AR₁,R₂,.,R_p} o multime de scheme de relatii si R R₁R₂.R_p . Relatia r(R) se numeste punct fix al transformarii de proiectie-unire daca (r) r . Multimea tuturor punctelor fixe ale transformarii ( . ) se noteaza cu FIX(R) .

Relatia s(R) din figura 2 este un exemplu de punct fix dat de schema : R A ABC, BC, ADE }. A spune ca r satisface J-dependenta *aRs este acelasi lucru cu m_R(r) r . In continuare se prezinta cateva proprietati ale PJ-transformarii m_R( . ) .

Propozitia 1. Fie o multime de scheme de relatii R AR₁,R₂,.,R_p}, R R₁R₂.R_p si relatiile r si s de schema R . PJ-transformarea are urmatoarele proprietati:

i) r m_R ( r ),

ii) daca r s atunci m_R( r )m_R( s ) ( monotonie ),

iii) m_R( r ) m_R (m_R( r ) ) ( idempotenta ).

Demonstratie: Punctul i) rezulta din definitia PJ-transformarii . Punctul ii) rezulta din proprietatea de monotonie a proiectiei , adica daca rs atunci _Ri(r)_Ri(s) 1ip . Fie r'= m_R(r) atunci iii) rezulta din proprietatea de completitudine a unirii lui _R1(r)_R2(r) _Rp(r)

Trebuie studiat cazul, in care o relatie de schema R poate fi reprezentata printr-o baza de date de schema R astfel ca sa satisfaca urmatoarele conditii :

C1) sa nu existe pierderi de informatii ;

C2) sa fie eliminata redundanta .

In practica nu este interesanta multimea tuturor relatiilor posibile de schema R ci numai cateva submultimi , notam una din ele cu P . Multimea P satisface conditia (C1) daca m_R(r) r pentru orice relatie rP , adica P FIX(R) . A doua conditie (C2) poate fi exprimata astfel : proiectiile oricarei relatii r din P in raport cu schemele din R sa aiba cel putin atatea tupluri cat r . Deoarece P este infinta ea nu poate fi descrisa prin enumerare ci numai prin specificarea multimii de restrictii de tip F- sau J- pe care relatiile componente le satisfac . In continuare notam cu C o multime de restrictii ( conditii ) pentru schema de relatie R .

Definitia 3. Multimea tuturor relatiilor r(R) care satisfac toate restrictiile din C se numeste SAT_R(C) . Daca schema R se subantelege atunci acesta se noteaza SAT(C) , iar cea pentru o singura conditie se noteaza cu SAT(c) .

Definitia 4. Fie C o multime de restrictii pentru o schema de relatie R . Spunem ca C implica c si notam Cc daca SAT_R(C)SAT_R (c) .

Daca P SAT_R(C) pentru o multime de restrictii C , atunci conditia (C1) de eliminare a pierderilor de informatii pentru baza de date de schema R poate fi formulata prin una din urmatoarele conditii : SAT(C)FIX(R) sau C *aRs. In paragraful urmator se da o metoda de verificare a acestor conditii cand C este formata dintr-o multime de F- si J-dependente .

3 . Tablouri

In acest paragraf se prezinta o metoda de reprezentare a unei PJ-transformari printr-un tablou. Tabloul este similar unei relatii cu deosebirea ca, in locul valorilor, tabloul contine variabile dintr-o multime oarecare V , care este reuniunea a doua multimi V_d si V_n , unde V_d este o multime de variabile principale ( distinguished ) notate cu litera a cu indice si V_n este o multime de variabile secundare notate cu litera b cu indice . Multimea atributelor este data de numele coloanelor tabloului care formeaza schema tabloului. Fiecare variabila principala apartine numai unei coloane. Tuplului dintr-o relatie ii corespunde o linie dintr-un tablou . Pentru un tablou de schema A₁A₂.A_n variabile principale din coloana A_i 1in sunt a_i . Un tablou T de schema R poate fi privit ca paternul (sau sablonul ) unei relatii de schema R . Dam relatia ce se obtine dintr-un tablou inlocuind variabilele cu valori din domeniile respective . Presupunem ca R R₁R₂.R_n si cu D_i dom (A_i) unde 1in . Se numeste evaluare (valoare, estimare ) a tabloului T o functie  : V D , astfel ca (v)dom (A_i) , daca v este o variabila care apartine coloanei . Se extinde evaluarea de la variabilele la linii si apoi la intreg tabloul. Daca w <w₁,w₂,.,w_n> este o linie a tabloului atunci (w) <w₁₎,w₂),.,w_n )> este o evaluare a liniei w. Notam cu  : ( t ) A(w) | w este linie in T } .

Exemplul 1.Fie tablou T din figura 1 , valoarea din figura 2 si (T) in figura 3 .

T (  ( r (

    2 5 6 9

    3 4 6 8

    2 5 6 8

 (

Figura 1 Figura 2 Figura 3

Vom interpreta un tablou T de schema R ca o functie de relatie de schema R . Fie w_d linia formata numai din variabile principale w_d < a₁,a₂,.,a_n > care nu este in mod necesar in T . Daca r este o relatie de schema R , punem

T (r) A(w_d) | (T) r }.

Aceasta definitie arata ca , daca avem o evaluare  care face sa corespunda oricarei linii din T un tuplu din r atunci  (w_d) este in T ( r ) .

Exemplul 2.Fie relatia din figura 4 si tabloul T din figura 1 si evaluarea din figura 2 arata ca tuplul <2,4,6,8> trebuie sa fie in T (r) . Evaluarea' din figura 5 pune <3,5,6,8> in T(r). T(r) este relatia s din figura 6.

R( ) T( r ) s (

2 5 6 9    

3 4 6 8 3 5 6 8

2 5 6 8    

3 4 7 8

Figura 4 Figura 5 Figura 6

Cand se evalueaza T(r) , daca coloana A_i din T nu contine variabile principale atunci in ea nu exista nici o restrictie asupra valorilor lui (a_i).

Daca  (T)r atunci ' (T)r pentru orice ' care coincide cu  pe V exceptand a_i . Prin urmare daca dom(A_i) este infinit, atunci T(r) poate avea o multime infinita de tupluri si nu este o relatie. De aceea cand se considera un tablou ca o functie trebuie ca in T sa aiba un simbol principal in fiecare coloana .

4 . Tabloul ca reprezentare a unei PJ-transformari

Pentru orice PJ-transformare m_R exista un tablou T care, ca functie coincide cu m_R . Fie R AR₁,R₂,.,R_p} o multime de scheme de relatie unde R R₁R₂.R_p A₁A₂.A_n . Tabloul determinat de schema bazei de date R notat T_R are p linii si este definit in urmatorul mod :

. schema lui T_R este R ;

T_R are p linii w₁,w₂,.,w_p ;

. linia w_i are in coloana A_j o variabila principala a_j daca A_jR_i ;

. Restul coloanelor din linia w_i 1ip sunt simboluri secundare unice

( adica nu apar in alte linii ale T_R ) ;

Aceasta transformare poate fi pusa sub forma urmatorului algoritmul :

0. START a TR-generarea tabloului T_R

1. INPUT A r , p ,n, R₁,R₂,.,R_p , A₁,A₂,.,A_n }

2. k 0

3. FOR i 1 , 2 , . . . , p

3.1 FOR j 1 , 2 , . . . , n

3.1.1 IF A_jR_i

THEN

.1 w_{i j} ' a _j '

ELSE

.2 k k + 1

.3 w_{i j} ' b_k '

3.1.2 CONTINUE

3.2 CONTINUE

4. OUPUT A w }

STOP

Exemplul 1.Fie R AA₁A₂,A₂A₃,A₃A₄} . Tabloul T_R este dat in figura 1 :

( )

    _b4

Figura 1

Propozitia 1. Fie R AR₁,R₂,.,R_p} o multime de scheme de relatie si R R₁R₂,.,R_p. Tabloul T_R si transformarea m_R definesc aceeasi functie de relatie de schema R .

Demonstratia rezulta din definitia transformari conservative .

Exemplul 2 Fie R A A₁A₂,A₂A₃,A₃A₄} si relatia r din figura 2 atunci m_R(r) T_R (r) s unde s este data in figura 3 .

r( s(

2 5 6 8

3 4 6 8

Figura 2 Figura 3

5 . Echivalenta schemelor si a tablourilor

Definitia 1 . Fie T₁ si T₂ tablouri de schema R. Spunem ca T₁ *T₂ daca    T₁(r) T₂(r) pentru orice relatie r(R). Tablourile T₁ si T₂ sunt echivalente daca T₁* T₂ si T₂ *T₁ si se noteaza cu T₂ T₁ .

Definitia 2. Fie R A R₁,R₂,.,R_p} si S A S₁,S₂,.,S_q} doua multimi de scheme de relatie unde R R₁R₂,.,R_p S₁S₂,.,S_q . Se spune ca R acopera pe S notata RS , daca pentru orice schema S_j din S , exista R_i in R astfel ca R_i Ê S_j . Se spune ca R si S sunt echivalente daca RS si SR si se noteaza R~S .

Exemplul 1: Daca R AA₁A₂, A₂A₃, A₃A₄} si S A A₁A₂A₃, A₃A₄} atunci SR

Teorema 1.Fie multimile de scheme de relatie R AR₁,R₂,.,R_p} si S A S₁,S₂,.,S_q } unde R R₁R₂,.,R_p S₁S₂,.,S_q . Urmatoarele afirmatii sunt echivalente :

1 . m_R(r)m_s (r) oricare ar fi r(R) ,

2 . T_R*T_S ,

3. FIX(R)FIX(S) ,

4. RS .

Demonstratie.Din propozitia 1 rezulta ca (1) este echivalenta cu (2) . Vom arata ca (1) si (3) sunt echivalente. Din secventa de demonstrare rezulta ca (1)

d1) sFIX( R)

d2) s m_R (s)    ( din d1 ) ,

d3) m_R(s)m_S(s) ( din ipoteza ) ,

d4) sm_S(s)    ( din d2 si d3 ) ,

d5) sm_S(s ( din lema 1 ) ,

d6) s m_S(s) ( din d4 si d5 ) ,

d7) sFIX( S)

Aratam ca (3)(1). Adica din FIX( R) FIX( S) m_R(r)m_S (r) .

Fie r(R) , r' m_R(r) , din idempotenta rezulta m_R(r') r', deci r'FIX( R) din ipoteza rezulta ca r'FIX( S) adica (a) m_S(m_R(r)) m_R(r). Dar m_R(r)r, din monotonia lui m_S rezulta (b) m_S(m_R(r))m_S(r) ; din (a) si (b) rezulta ca m_S(r) m_R(r) .

Vom arata ca conditiile (1) si (4) sunt echivalente. Presupunem ca, dom(A) contine cel putin doua valori pentru orice atribut A din R. Notam aceste valori cu 0 si 1. Construim relatia s(R) cu q tupluri t₁,t₂,.,t_q definite in urmatorul mod :

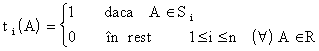
Notam cu t₀ tuplul format numai din valori nule . Nu este greu de verificat ca apartine lui m_S(s). Prin urmare t₀m_R(s). Conform definitiei lui m_R, pentru fiecare schema R_i din R exista un tuplu t_js astfel ca t_j(R_i ) t₀(R_i). Astfel R_iS_j deci RS .

Presupunem ca RS . Fie r(R) o relatie arbitrara si t un tuplu arbitrar din m_S(r). In r exista tuplurile t₁,t₂,.,t_q astfel ca t_i(S_i) t(S_i), 1iq. Deoarece RS atunci pentru orice R_j din R exista S_i , S_iR_j, prin urmare t_i(R_j) t_i(S_i) . Fie tuplurile t_j'r , t_j'(R_j) t(R_{j )} din care rezulta ca t este din m_R(r) si prin urmare m_R(r)m_S(r) .

Exercitiu.Fie R AA₁A₂ A₂A₃ A₃A₄} si S A A₁A₂A₃ A₃A₄} . Daca RS se observa ca T_R(r) T_S(r) . Fie relatia r(R) din figura 1 si tablourile T_R(r) si T_S(r) .

r(

2 5 7 9 2 5 7 9 2 5 7 9

3 4 8 10 2 5 8 10 3 5 8 10

4 6 8 11 2 5 8 11 3 5 8 11

3 5 7 9 4 6 8 10

3 5 8 10 4 7 8 11

3 5 8 11

4 6 8 10

4 6 8 11

Figura 1 Figura 2 Figura 3

Corolar 1.Fie multimile de scheme de relatie R AR₁,R₂,.,R_p} si S A S₁,S₂,.,S_q} unde R R₁,R₂,.,R_p S₁,S₂,.,S_q . Urmatoarele afirmatii sunt echivalente :

1 . m_R m_S

2 . T_RT_S

3. FIX(R)FIX(S) ,

4. R~ S .

Prin conditia (1) intelegem m_R(r) m_S(r) pentru orice r(R) .

Fie R AA₁A₂A₃,A₁A₄,A₁A₃A₄} si S A A₁A₂A₃,A₃A₄,A₁A₃A₄}. Multimile de scheme de relatie R si S sunt echivalente. Din corolarul 1 rezulta ca T_RT_S , dar evident ca T_RT_S. Cum se observa din exemplul urmator chiar daca se vor redefini variabilele secundare .

   

   

   

Figura 1 Figura 2

Definitia 1. Fie w₁ si w doua linii ale tabloului T de schema R . Daca pentru orice atribut A din R cu w₂(A) principala rezulta ca w₁(A) este variabila principala si se spune ca w₁ absoarbe ( subsume ) w₂ .

Definitia 2. Fie T un tablou. Tabloul in care liniile nu mai pot fi ( reduse ) absorbite de nici o alta linie se numeste redus prin absortie si se noteaza cu SUB(T) .

Exemplul 1. In tabloul T_R w₁ absoarbe w₂ deoarece w₁(A₁) a₁ w₂(A₁) a₁ w₁(A₄) a₄ w₂(A₄) a₄ atunci :

SUB( ) SUB(

   

Teorema 1 . Fie multimile de scheme de relatie R AR₁,R₂,.,R_p} si S A S₁,S₂,.,S_q} unde R R₁,R₂,.,R_p S₁,S₂,.,S_q . Atunci:

T_RT_S SUB(T_R) SUB(T_S) exceptand variabilele secundare.

2) SUB(T_R T_R

Pentru demonstratie vezia s.

5. C-Transformari

Teorema 1 arata ca exista un procedeu simplu pentru verificarea echivalentei a doua tablouri obtinute din multimi de scheme si anume verificarea identitatii reduse prin absortie. Orice tablou in care nici o variabila secundara nu se intalneste mai mult decat o data se obtine dintr-o multime oarecare de scheme. Teorema 1 nu este adevarata pentru tablourile unde variabilele secundare sunt duplicate .

Dorim sa formulam conditii de echivalenta pentru tablouri arbitrare introducand c-transformarea pentru tablouri. C-transformarea este asemanatoare evaluarii (estimarii) , care in locul transformarii variabilelor tabloului in elemente ale domeniului ele se transforma in variabile ale altui tablou . Prin urmare liniile se transforma in linii .

Definitia 1 : Fie T si T' doua tablouri de schema R si multimile de variabile V si V'. Transformarea y:V->V' se numeste C-transformare din T in T' daca ea satisface urmatoarele conditii :

1) daca variabila v se afla in linia A a tabloului T atunci y(v) se afla in linia A a tabloului T' ;

2) daca v este o variabila principala atunci y(v) este variabila principala ;

y(v)T' . Adica , daca y este extinsa la liniile lui T si deci la intregul tablou T atunci prin aceasta transformare o linie din T se transforma intr-o linie din T' .

Exemplul 1 : Fie tablourile T si T' din figura 1 si 2 si c-transformarea din figura 3

T( ) T'(

y i

y y

y y y

Figura 1 Figura 2 Figura 3

Primele doua linii din T sunt aplicate in primele doua linii din T' de y , c-transformarea y aplica a treia linie dinT in a doua linie din T' .

Teorema 1 : Fie tablourile T si T' de schema R . T *T' daca si numai daca exista o c-aplicatie de la T la T' .

Demonstratie : Suficienta . Fie y o aplicatie de la T la T'. Fie r(R) o relatie oarecare , T(r) si T'(r) . Daca  este o evaluare a lui T' astfel ca (T')r , atunci  y este o evaluare pentru T ,  y(T)r . Incluziunea rezulta din y(T)T' prin aplicarea lui . Daca w_d este o linie formata din variabile principale si y( w_d) w_d (y(w_d)) (w_d) deci T'(r) T(r).

Necesitatea . Presupunem ca T T'. Considerand tabloul T' ca relatie obtinem T(T')T'(T') Luand evaluarea' care este transformarea identica a variabilelor V' din T' . Evident'(T') T'T' si'(w_d) w_dT'(T'). Exista o evaluare  pentru T astfel ca (T) T', (w_d) w_d . Atunci definim c-aplicatia din T la T' prin.

Corolar : Fie T si T' doua tablouri de schema R .T T' exista o C-transformare de la T la T' si o C-transformare de la T' la T .

Exemplul 2: Fie T tabloul care este compus numai dintr-o linie formata numai din variabile principale w_d si T' un tablou care contine w_d , atunci T T' . C-transformarea din T la T' aplica w_d in w_d . C-transformarea din T' in T aplica toate liniile in w_d .

6 . Echivalenta schemelor determinata de restrictii

In acest paragraf se determina care sunt proprietatile unei relatii care sa fie corect reprezentata prin proiectiile sale. Din corolarul teoremei 1 3 rezulta ca, daca R AR₁,R₂,.R_p} este o schema a bazei de date atunci FIX(R) este multimea tuturor relatiilor pe R R₁,R₂,.R_p numai daca R_i R pentru un i anumit. In multe cazuri dorim sa reprezentam o multime de relatii pentru schema R asupra careia se aplica o multime impusa de restrictii . Vom utiliza restrictiile ca sa reprezentam relatiile .

Definitia 1 : Fie P o multime de relatii de schema R . Daca T₁ si T₂ sunt tablouri de schema R atunci T₁ cuprinde T₂ in raport cu P ( notat T₁ T₂ ) daca T₁(r) T₂ (r) , rP .

T₁T₂ ( sunt echivalente pe P ) daca T₁ T₂ si T₂ T₁ .

In majoritatea cazurilor se considera P SAT(C) pentru o multime de restrictii C data. Notam pe scurt pe prin . Ne intereseaza cand SAT(C)FIX(R) pentru o schema a bazei de date R . Adica pentru o schema a bazei de date R putem sa descompunem fara pierdere pe R orice relatie din SAT(C) . In termenii restrictiilor aceasta se poate reduce la verificarea corectitudinii relatiei C *aRs. Daca T_I este un tablou pentru transformarea identica (T_I contine linia formata din variabile principale), atunci dorim sa stim daca T_R se comporta ca T_I pe SAT(C) adica T_RT_I ? Teorema 1 din &5 da un test pentru * dar ne trebuie un test pentru . Pentru lema urmatoare va trebui sa privim un tablou ca o relatie care este din multimea P. Prin aceasta se intelege ca pentru orice evaluare  , (T)P Pentru o multime arbitrara de relatii aceste conditii sunt mai greu de verificat . Totusi caand P=SAT(C) unde C consta intr-o multime de F- sau J-dependente daca pentru o evaluare bijectiva ,(T)P , atunci pentru orice alta evaluare','(T)P .

Lema 1: Fie T₁ si T₂ doua tablouri de schema R si P o multime de relatii pe R . Fie T₁' si T₂' astfel ca :

1) T₁ T₁' si T₂T₂'si

2) T₁' si T₂' considerate ca relatii sunt ambele din P .

Atunci T₁* T₂ daca si numai daca T₁' * T₂' .

Demonstratie : Suficienta este directa . Daca T₁'* T₂' atunci rezulta ca T₁' T₂', dar T₁ T₁'si T₂ T₂' deci T₁ T₂ . Vom arata ca, daca T₁ T₂ atunci T₁'* T₂' . Considerand T₁' simultan ca relatie si tablou atunci T₁'(T₁') este din P si T₁'(T₁') T₂'(T₂') . Fie w_d o linie a tuturor variabilelor principale si  o evaluare identica a lui T₁'. Evident (T₁') T₁' astfel este in T₁'(T₁') prin urmare si in T₂(T₁') . Exista o evaluare pentru T₂' astfel ca( T₂') T₂' si ( . Evaluarea poate fi considerata ca o c-transformare din T₂' in T₁' si prin urmare rezulta T₁ * T₂'.

Corolar : In ipotezele lemei 1 rezulta ca T₁ T₂ daca si numai daca T₁' T₂' .

Acest corolar poate fi interpretat ca un test de verificare a relatiei T₁ T₂ , daca printr-un procedeu am afla tabloul T' , astfel ca T'T si T' ca relatie este in SAT(C). Vom introduce reguli de transformare pentru tablouri . O regula de transformare determinata de o multime de restrictii C este un procedeu de modificare a tabloului T in tabloul T' astfel ca TT' . Prima transformare particulara a fost c-transformarea prin absortie. Pentru un tablou T cu variabile secundare ne duplicate eliminarea liniilor absorbite conserva echivalenta. Va trebui sa gasim multimea regulilor de transformare ( F-reguli si J-reguli) pentru o multime data C de F-dependente si J-dependente. Aplicarea repetata a acestor reguli de transformare are ca rezultat obtinerea unui tablou care satisface toate dependentele din C. In continuare vom considera o multime C de F- si J-dependente pentru o multime U de atribute care constituie schema pentru toate restrictiile si tablourile considerate. Oricarei F-dependente XA din C ii este asociata o F-regula . F-regula determinata de XA reprezinta o clasa de transformari care poate fi aplicata unui tablou care nu depinde de liniile alese. Fie un tablou T care contine liniile w₁ si w₂ unde w₁(x) w₂(x) si v₁ w₁(A) si v₂ w₂ (A), v₁v₂ .

A aplica o F-regula determinata de F-dependenta XA la tabloul T, inseamna a identifica variabilele v₁ si v₂ si a inlocui una din ele prin alta in urmatorul mod :

- daca una din v₁ si v₂ este principala, sa zicem v₁ instanta lui v₂ este inlocuita cu v₁.

- daca v₁ si v₂ nu sunt principale atunci orice instanta cu indice mai mare este inlocuita cu instanta variabilei cu indice mai mic .

Deoarece tabloul este o multime de linii , cateva din ele prin redefinire vor fi identice si vor fi eliminate .

Exemplul 1 : Fie tabloul T din figura 1 si C AA₁A₂ A₄ , A₂A₄ A₃}. Aplicand F-regula determinata de A₂A₄ A₃ la liniile 1 si 2 permitem inlocuirea variabilei b₃ cu a₃ deoarece a₃ este principala si obtinem tabloul T' .

T( ) T'( ) T"(

Figura 1 Figura 2 Figura 3

Aplicand F-regula determinata de A₁A₂ A₄ se obtine tabloul T" deoarece variabile b₁ si b₄ trebuie identificate prin cea cu indice mai mic . Astfel prima si ultima linie sunt identice deci se elimina una din ele .

Teorema F. Fie T' tabloul rezultat prin aplicarea unei F-reguli date de X A din tabloul T . Atunci T si T' sunt echivalente pe SAT(X A) .

Fie S AS₁,S₂,.,S_l} o multime de scheme de relatii si *aSs o J-dependenta pe U. Fie T un tablou si w₁,w₂,.,w_q liniile lui T care sunt unibile pe S cu rezultatul w . Aplicarea J-regulii *aSs la T inseamna formarea tabloului T' TAw}.

Exemplul 3. Fie T tabloul reprezentat in figura 4 si C A*aA₁A₂A₄, A₁A₃A₄s , *aA₁A₂, A₂A₃, A₃A₄s} . Aplicand J-regula determinata de *a A₁A₂, A₂A₃, A₃A₄s la a doua si a treia linie din T genereaza linia <a₁ b₁ b₃ a₄> . Rezultatul este tabloul T' dat in figura 5 .

T( ) T'( ) T"(

Figura 4 Figura 5 Figura 6

J-regula data de *aA₁A₂A₄, A₁A₃A₄s poate fi aplicata la prima si a patra linie a lui T'; se genereaza linia <a₁ b₁ b₃ a₄> iar tabloul T' este rezultatul acestei aplicatii.

Teorema J. Fie S AS₁,S₂,.S_q}. Fie T' tabloul rezultat prin aplicarea J-regulii determinata de *aSs din tabloul T . Atunci tablourile T si T' sunt echivalente pe SAT(*aSs).

Demonstratie : Va trebui sa aratam ca T(r) T'(r) pentru orice rSAT(*aSs) . Fie t'T'(r) si  o evaluare cu (w_d) t' si (T')r . Deoarece TT' avem (T)(T') de asemenea (T')r si(w_d) t'T(r) . Prin urmare T'(r)T(r) . Acum fie t un tuplu oarecare din T(r) si  o evaluare cu (w_d) t si (T)r . Tuplul unic care ar putea apartine lui(T') dar nu lui(T) este(w) unde w este generata de J-regula determinata de *aSs din liniile w₁,w₂,.,w_q care apartin lui T. Daca w₁,w₂, .,w_q sunt unibile pe S atunci (w₁), (w₂),.,(w_q) unite pe *aSs dau rezultatul w. Intrucat r intra in SAT(*aSs) si (w₁) ,(w₂),.,(w_q)Tr atunci (w)r. Prin urmare(T')r si(w_d) tT(r), deci T(r)T'(r) si deci T(r) T'(r).

7. Algoritmul chase

In acest paragraf se da un algoritm de calcul care se bazeaza pe metoda chase , cu ajutorul careia pentru un tablou dat si o multime de dependente C se construieste un nou tablou T* astfel ca TT* si T* ca relatie sa apartina lui SAT(C) . Pentru un tablou T si o multime de dependente C se aplica regulile determinate de F- si J-dependentele din C atata timp cat se realizeaza schimbari . Ordinea de aplicare este neesentiala . Conform teoremelor F si J la terminarea algoritmului se genereaza un tablou T*T si T*SAT(C) .

Procedura TR transforma tabloul T_j+i in T_j+i+1 pe baza regulei determinata de dependenta C_i. Functia DIF determina daca exista o diferenta intre doua transformari succesive . Dam algoritmul chase in detaliu :

0 START a Chase s

1 INPUT a T , k , C₁,C₂,.,C_ks

2 n

3 T_n T

4 d

5 WHILE d

5.1 d

5.2 FOR i 1 , 2 , k

5.1.1 CALL TR(T_n,C_i;T*)

5.1.2 IF DIF(T_n,T')

THEN

.1 nn+1

.2 T_nT'

.3 d =0

. 5.1.3 CONTINUE

5.4 CONTINUE

6 OUPUT AT_n}

7 STOP

Fie tabloul T din figura 1 si C AB C,ADC,*a BCD , ABCs}. Aplicand F-regula determinata de B C se obtine T₁ din figura 2 . Aplicand J-regula *aABC, BCDs se obtine T₂ din figura 3 . Aplicand F-regula determinata de AD C se obtine T₃ din figura 4 .

T ( A B C D) ( A B C D ) ( A B C D ) (A B C D ) T*( A B C D )

Figura 1 Figura 2 Figura 3 Figura 4 Figura 5

Aplicarea J-regulii determinata de *aABC , BCDs lui T₃ permite obtinerea lui T* si orice alta regula il lasa invariant . Astfel T* este ca relatie in SAT(C) .

Definitia 1: Se numeste secventa generata din T prin aplicarea regulilor ( F- sau J) determinate de dependentele din C , secventa T T,T₁, . . . unde T_i+1 se obtine din T_i prin aplicarea unei F- sau J-dependente determinate de o dependenta din C , se presupune T_iT_i+1 . Daca secventa generata are un ultim element T_n astfel ca orice F- sau J-dependenta determinata de C aplicata nu-l mai schimba atunci T_n este numit chase-ul lui T in raport cu C . (T) reprezinta multimea chase-urilor .

Exemplul 2 : Fie T si C din exemplul 1. T , T₁ , T₂ , T₃ si T* este o secventa generata din T de C si T*IChase_C(T) . Va trebui sa observam cum se transforma liniile pe parcursul aplicarii algoritmului Chase . Fie T' obtinut din T prin aplicarea unei J-reguli . Atunci daca w este o linie a lui T ei ii corespunde in T' aceeasi linie sau are in plus o linie obtinuta prin unirea unui numar de linii . Fie T' derivat din T prin aplicarea unei F-reguli care schimba variabila v cu variabila v' . Daca w este o linie in T ii corespunde in T' o linie w' care este de fapt w in care s-a inlocuit v cu v'. ( Daca w nu contine v atunci w w' ) .