Adunarea, scaderea si inmultirea numerelor intregi

Adunarea, scaderea si inmultirea numerelor intregi

Aceste operatii se executa folosind reprezentarea in complement fata de 2 a numerelor intregi, sau, mai bine zis, se executa folosind in algoritmi bitul de semn ca pe un bit obisnuit.

De exemplu, dorim sa calculam:

37-25

25-37

(-25)x37

(-25)x(-37)

Pentru efectuarea acestor calcule, vom scrie reprezentarile cu bit de semn ale numerelor implicate:

Se observa ca 25 si (-25) se reprezinta pe 6 biti iar 37 si (-37) pe 7 biti.

Deoarece am observat ca bitii unui intreg cu semn nu au toti aceeasi semnificatie, este nevoie sa reprezentam numerele cu care lucram pe un acelasi numar de biti. La adunari sau scaderi, bitii de semn se vor afla in aceeasi pozitie (vor avea aceeasi pondere) si vom obtine astfel rezultate corecte. Pentru a avea o scriere pe un acelasi numar de biti, se adauga (completeaza) la stanga bitul de semn de un numar corespunzator de ori. Astfel:

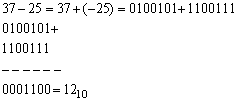
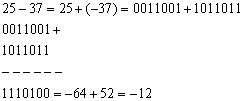
In continuare vom pune in evidenta importanta gamei de reprezentare, adica a domeniului de valori ale datelor. Sa consideram, spre exemplu, adunarea a doua numere cu semn reprezentate pe un octet (8 biti). Aceste numere sunt cuprinse in gama

.

Daca vom dori sa adunam doua numere din acest domeniu si sa reprezentam rezultatul tot pe un octet, putem avea surprize. De exemplu, sa consideram operatiile (117-12) si (117+12). Se observa ca operanzii sunt in gama de reprezentare a numerelor cu semn pe 8 biti. Prin prima scadere, ne asteptam sa obtinem un rezultat, 105, in aceeasi gama de reprezentare.

117-12=117+(-12) = 01110101+11110100 = 01101001 = 105₁₀, rezultat corect.

117+12 = 01110101+00001100 = 10000001 = -127₁₀,

rezultat evident incorect.

Incorectitudinea provine de la faptul ca rezultatul a depasit gama de reprezentare. Daca rezultatul este interpretat pe 9 biti de exemplu, gama de reprezentare devine si rezultatul va fi

117+12 = 001110101+000001100 = 010000001 = 129₁₀, rezultat corect.

Ca o concluzie preliminara, retinem ca pentru a obtine rezultate corecte este necesar sa precizam daca se lucreaza sau nu cu bit de semn si pe cati biti se face reprezentarea, pentru ca numai in acest context interpretarea rezultatelor este corecta.

In ceea ce priveste inmultirea numerelor intregi cu semn (cu bit de semn), aici problema nu mai are o rezolvare asemanatoare, in sensul ca nu putem trata bitii de semn la fel cu cei de reprezentare ai valorii. Astfel, procesorul studiaza bitii de semn si ia o decizie in privinta semnului rezultatului. De fapt, se realizeaza functia logica XOR a bitilor de semn. Numerele negative se vor lua in modul, iar operatiile de inmultire se vor face numai cu numere pozitive. La final, functie de semnul rezultatului, se ia decizia reprezentarii corecte a rezultatului.

Spre exemplu, sa calculam (-25)x37. Pentru aceasta, procesorul va primi pentru procesare urmatoarele doua numere:

Se analizeaza separat bitii de semn si se ia decizia ca rezultatul va fi negativ, deci, la final, se va reprezenta in complement fata de 2. Mai departe se va lucra cu 25, modulul numarului (-25), care se obtine prin complementarea fata de 2 a numarului binar 1100111:

à

Se va retine pentru procesare numai numarul (fara semn) 11001, care se va inmulti cu numarul (fara semn) 100101, obtinand, asa cum am aratat mai sus, valoarea 1110011101. Mai departe, se adauga bitul de semn, 0 pentru numere pozitive, obtinandu-se 01110011101. Acest ultim numar se va complementa fata de 2, obtinandu-se 10001100010+1=[1]0001100011, adica valoarea -1024+99 = -925, valoarea corecta.

Ca o concluzie, pentru a furniza rezultate corecte, procesorul va trebui informat in permanenta despre ce fel de numere prelucreaza (cu sau fara semn) si care este lungimea lor de reprezentare (toate trebuie sa aiba aceeasi lungime).

Reprezentarea in complement fata de 2 se poate folosi si pentru numerele reale negative, bitul de semn fiind MSB de la partea intreaga. Astfel, -12.25 poate avea reprezentarea:

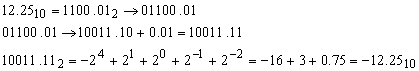Pentru inmultirea numerelor reale raman valabile considerentele de la numere intregi.

In cazul de mai sus, problema reprezentarii numarului negativ a fost rezolvata cu ajutorul bitului de semn dar problema reprezentarii punctului binar va avea alta rezolvare.