Metoda backtracking

Metoda backtracking

Prezentarea metodei

Metoda backtracking (in traducere "cautare cu revenire") se aplica problemelor in care solutia se poate reprezenta sub forma unui vector s = (s₁, , s_n), s I S, S = S₁ x x S_n. Multimea S_k are n_k elemente, k = 1, , n. O solutie s I S se numeste solutie posibila si S se numeste spatiul solutiilor posibile. In orice problema concreta sunt date anumite relatii intre componentele s₁, , s_n, ale vectorului s, numite restrictii interne. Solutiile posibile care satisfac restrictiile interne se numesc solutii admisibile. In probleme se cere determinarea tuturor solutiile admisibile sau numai a uneia dintre ele, numita solutie optima, care optimizeaza o functie obiectiv data.

Observatii

Nu in toate problemele care pot fi rezolvate cu metoda backtracking se cunoaste de la inceput numarul n al multimilor S₁, , S_n.

Componentele s₁,,s_n ale vectorului solutie s pot fi la randul lor vectori.

In unele probleme, multimile S₁, , S_n coincid.

O metoda simpla de determinare a solutiilor admisibile consta in a genera, intr-un mod oarecare, toate solutiile posibile si de a le selecta doar pe cele care verifica restrictiile interne. Dezavantajul acestei metode este timpul necesar de investigare exhaustiva care este foarte mare. Astfel, chiar pentru n_k = 2, k = 1, , n, timpul necesar este θ(2ⁿ), deci exponential.

Metode backtracking evita generarea tuturor solutiilor posibile. Aceasta metoda construieste o solutie admisibila, pas cu pas, prin adaugarea unei componente s_k I S_k la o solutie partiala (s₁, , s_k-1) numita solutie acceptabila. Daca solutia partiala (s₁, , s_k-1, s_k) verifica anumite conditii, numite conditii de continuare, atunci aceasta solutie partiala devine noua solutie acceptabila.

Ideea generala a metodei backtracking consta in urmatoarele:

(s₁) este solutie acceptabila;

k:=2;

cat timp mai sunt elemente netestate in S₁

daca mai exista element netestat s_k din S_k atunci

daca (s₁, , s_k) indeplineste conditiile de continuare atunci

daca (s₁, , s_k) este solutie admisibila atunci

tipareste (s₁,,s_k)

altfel (s₁,,s_k) este solutie acceptabila si se alege un element     netestat din S_k+1

altfel (s₁, , s_k-1) este solutie accetabila si se alege un element netestat din S_k

altfel (s₁, , s_k-2) este solutie accetabila si se alege un element netestat din S_k-1;

Conditiile de continuare sunt in stransa legatura cu restrictiile interne si le formalizam prin functiile:

c_k : S₁ x x S_k → , k = 1, ., n

Metoda backtracking este prezentata in procedura BACKTRACK, care apeleaza procedura CONDCONT ce testeaza conditiile de continuare.

PROCEDURA CONDCONT(n, s, k, v);

BEGIN

ARRAY s(n);

IF c_k( s₁, , s_k) = 1

THEN v := 1

ELSE v := 0;

ENDIF;

END

PROCEDURA BACKTRACK(n, s);

BEGIN

ARRAY s(n);

k := 1;

WHILE k > 0 DO

WHILE exista element netestat e_i din S_k DO

s_K := e_i;

CONDCONT(n, s, k, v);

IF v = 1 THEN

IF k = n

THEN WRITE( s )

ELSE k := k + 1;

ENDIF;

ENDIF;

ENDWHILE

k := k - 1;

ENDWHILE;

END;

Observatii

Daca inlocuim predicatul c_k cu 1 pentru orice k = 1, , n, atunci vor fi listate toate solutiile posibile ale problemei.

Metoda backtracking poate fi reprezentata pe un arbore radacina construit in modul urmator:

nivelul 0 contine nodul radacina r;

fiecare nod x de pe nivelul k - 1 are n_k succesori y₁, , , k = 1, , n si arcul (x, y_i) este etichetat cu elementul e_i din S_k, i = 1, , n_k;

nivelul n contine n = n₁ n₂ n_n noduri si pentru fiecare nod terminal, drumul D = (s₁, , s_n), s_k I S_k, k = 1, , n reprezinta o solutie posibila;

determinarea solutiilor admisibile cu metoda backtracking corespunde parcurgerii DF (mai intai in adancime) a arborelui radacina

Teorema 4.2

Metoda backtracking are complexitatea exponentiala.

Demonstratie

Evident

Probleme rezolvate

Problema B1

Colorarea hartilor

Fiind data o harta cu n tari, se cere sa se genereze toate solutiile de colorare a hartii cu m culori astfel incat pentru fiecare tara sa se foloseasca o singura culoare si doua tari vecine (cu frontiera comuna) sa fie colorate diferit.

Observatie

Este demonstrat faptul ca sunt suficiente 4 culori pentru colorarea tarilor conform enuntului problemei.

Rezolvarea problemei cu metoda backtracking

Configuratia hartii este furnizata cu ajutorul unei matrice H = (h_ij)_nxn,

daca tara i este vecina cu tara j,

in caz contrar.

Fie C = = multimea celor m culori si T = multimea celor n tari. Elementele problemei sunt urmatoarele:

S_k = C, k = 1, , n

o solutie posibila este de forma s = (s₁, , s_n), s_k I C, k = 1,,n;

restrictiile interne sunt: s_i s_j daca h_ij = 1, i = 1,,n, j = 1,,n;

conditiile de continuare sunt: s_i s_k pentru orice tara i din T, vecina cu tara k.

Algoritmul de colorare este prezentat in procedura COLOR care apeleaza procedura CONDCONT ce testeaza conditiile de continuare.

PROCEDURA COLOR(n, s, m, H);

BEGIN

ARRAY s(n); H(n,n);

k := 1; s₁ = 0;

WHILE k > 0 DO

WHILE s_k < n DO

s_k := s_k + 1;

CONDCONT(n, s, k, v, H);

IF v = 1 THEN

IF k = n THEN

WRITE( s )

ELSE

BEGIN

k := k + 1; s_k := 0;

END;

ENDIF

ENDIF;

ENDWHILE;

k := k - 1;

endWHILE;

END;

PROCEDURA CONDCONT(n, s, k, v, H);

BEGIN

ARRAY s(n); H(n,n);

v := 1;

FOR i := 1 TO k - 1 DO

IF h_ik = 1 and s_i = s_k THEN

v:=0; EXIT;

ENDIF;

ENDFOR;

END;

Fie harta cu multimea tarilor T si multimea culorilor C prezentate in figura 4.2. Arborele radacina asociat metodei backtracking pentru rezolvarea problemei colorarii acestei harti este prezentat in figura 4.3.

T = S₁ = S₂ = S₃ = C =

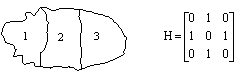
Figura 4.2

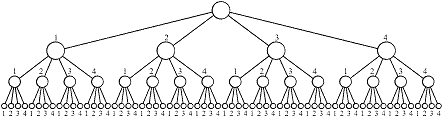
Figura 4.3

Solutiile admisibile obtinute cu procedura COLOR (parcurgerea DF a arborelui radacina) sunt urmatoarele:

s = (1, 2, 1); s = (1, 2, 3); s = (1, 2, 4); s = (1, 3, 1); s = (1, 3, 2);

s = (1, 3, 4); s = (1, 4, 1); s = (1, 4, 2); s = (1, 4, 3); s = (2, 1, 2);

s = (2, 1, 3); s = (2, 1, 4); s = (2, 3, 1); s = (2, 3, 2); s = (2, 3, 4);

s = (2, 4, 1); s = (2, 4, 2); s = (2, 4, 3); s = (3, 1, 2); s = (3, 1, 3);

s = (3, 1, 4); s = (3, 2, 1); s = (3, 2, 3); s = (3, 2, 4); s = (3, 4, 1);

s = (3, 4, 2); s = (3, 4, 3); s = (4, 1, 2); s = (4, 1, 3); s = (4, 1, 4);

s = (4, 2, 1); s = (4, 2, 3); s = (4, 2, 4); s = (4, 3, 1); s = (4, 3, 2);

s = (4, 3, 4);

Textul sursa al programului care implementeaza algoritmul prezentat mai sus este:

#include<stdio.h>

void afisare(int s[20], int n)

int cont(int s[20], int k, int h[20][20])

void back(int n, int m, int h[20][20])

k--;

}

void main()

back(n,m,h);

Problema B2

Problema permutarilor

Sa se afiseze toate permutarile de cate n elemente. De exemplu, pt n=3 acestea sunt 1, 2, 3 - 1, 3, 2 - 2, 1, 3 - 2, 3, 1 - 3, 1, 2 - 3, 2, 1.

Rezolvarea problemei cu metoda backtracking

Fie C = = multimea celor n obiecte. Elementele problemei sunt urmatoarele:

S_k = C, k = 1, , n

o solutie posibila este de forma s = (s₁, , s_n), s_k I C, k = 1,,n;

conditiile interne sunt: s_i s_j, i = 1,,n, j = 1,,n;

conditiile de continuare sunt: s_i s_k pentru orice obiect i din .

Algoritmul de generarea a permutarilor este prezentat in procedura PERM care apeleaza procedura CONDCONT ce testeaza conditiile de continuare.

PROCEDURA PERM(n, s);

BEGIN

ARRAY s(n);

k := 1; s₁ = 0;

WHILE k > 0 DO

WHILE s_k < n DO

s_k := s_k + 1;

CONDCONT(n, s, v);

IF v = 1 THEN

IF k = n THEN

WRITE( s )

ELSE

BEGIN

k := k + 1; s_k := 0;

END

ENDIF;

ENDIF;

ENDWHILE;

k := k - 1;

endWHILE;

END;

PROCEDURA CONDCONT(n, s, k, v);

BEGIN

ARRAY s(n);

v := 1;

FOR i := 1 TO k - 1 DO

IF s_i = s_k THEN

v:=0; EXIT;

ENDIF;

ENDFOR;

END;

Codul sursa al programului este:

#include<stdio.h>

void afisare(int s[20], int n)

int cont(int s[20], int k)

void back(int n)

k--;

}

void main()

Problema B3

Problema discreta a rucsacului.

Un hot sparge un magazin in care se gasesc n obiecte pe care si le-ar dori. Din pacate, greutatea lor totala depaseste capacitatea sacului pe care il are la dispozitie. Prin urmare, el este nevoit sa aleaga doar cateva din cele n obiecte. Hotul alege obiectele in functie de greutatea si valoarea lor, in asa fel incat valoarea finala a furtului sa fie maxima. Datele de intrare sunt: capacitatea rucsacului, numarul n de obiecte si pentru fiecare obiect in parte greutatea si utilitatea lui. Sa se afiseze obiectele furate de hot.

Rezolvarea problemei cu metoda backtracking

Fie C = = multimea celor n obiecte identificate prin valorile V = , si greutatile G = lor; capacitatea sacului este Capac;

Elementele problemei sunt urmatoarele.

S_k = C, k = 1, , n

o solutie posibila este de forma s = (s₁, , s_n), s_i I , i = 1,,n cu proprietatea ca ; daca s_i = 0 inseamna ca obiectul i nu este pus in sac, iar daca s_i = 1 inseamna ca obiectul i este pus in sac;

conditiile interne sunt: s_i s_j, i = 1,,n, j = 1,,n;

conditiile de continuare sunt: s_i s_k pentru orice obiect i din .

Algoritmul de determinare a multimii obiectelor furate este prezentat in procedura SAC care apeleaza procedura CONDCONT ce testeaza conditiile de continuare.

PROCEDURA SAC(n, s);

BEGIN

ARRAY s(n);

k := 1; s₁ := -1; C1 := 0; V1 := 0; Vmax := 0;

WHILE k > 0 DO

(6) WHILE s_k < 1 DO

(7) s_k := s_k + 1;

IF s_k = 1 THEN

BEGIN

C1:= C1 + g[k];

V1:= V1 + v[k];

END;

IF CONDCONT(s, k, C1) THEN

IF k = n THEN

IF C1 ≤ C and V1 > Vmax THEN

Vmax := V1;

retine(S, Smax);

ENDIF;

ELSE

BEGIN

k := k + 1; s_k := -1;

END;

ENDIF;

ENDIF;

ENDWHILE;

IF s_k = 1 THEN

BEGIN

C1:= C1 - g[k];

V1 := V1 - v[k];

END;

k := k - 1;

endWHILE;

END;

PROCEDURA CONDCONT(s, k, C1)

(2) BEGIN

IF s_k = 1 AND C1 > C THEN

return False

ELSE

return True

ENDIF;

(8) END;

Codul sursa al programului este:

#include<stdio.h>

typedef struct

obiect;

void afisare(int s[20], int n, obiect o[20])

int cont(int s[20], int k, double c, double c1)

void retine(int s[20], int smax[20], int n)

void back(int n, double c, obiect o[20])

if(cont(s,k,c,c1))

if(k==n)

}

else

s[++k]=-1;

}

if(s[k]==1)

k--;

}

afisare(smax, n, o);

void main()

back(n,c,o);