Metoda divide et impera

Metoda divide et impera

Prezentarea metodei

Metoda divide et impera (in traducere "imparte si stapaneste") consta in impartirea repetata a unei probleme de dimensiune mai mare, in doua sau mai multe subprobleme de acelasi tip, urmata de combinarea rezultatelor subproblemelor, pentru a obtine rezultatul problemei initiale.

Pentru precizari, sa presupunem ca se da un tablou A = (a₁,.,a_n) si ca trebuie efectuata o prelucrare oarecare asupra elementelor sale. Mai mult, presupunem ca pentru orice p, q naturali cu 1 p < q n, exista m natural cu p m q-1 astfel incat prelucrarea secventei se poate face prelucrand subsecventele , si apoi combinand rezultatele pentru a obtine rezultatul intregii secvente .

Varianta recursiva a metodei divide et impera este urmatoarea:

PROCEDURA DIVIMP(p, q, r);

BEGIN

IF q - p l

THEN PRELUC(p, q, r)

ELSE BEGIN

DIVIDE (p, q, m);

DIVIMP(p, m, r₁);

DIVIMP(m+1, q, r₂);

COMBIN(r₁, r₂, r);

END;

ENDIF;

END;

Avem urmatoarele semnificatii:

p q m s-au definit mai sus;

r reprezinta rezultatul secventei ;

l reprezinta lungimea maxima a secventei , pentru care prelucrarea se poate face direct;

PRELUC reprezinta numele procedurii care realizeaza prelucrarea secventei , furnizand rezultatul r;

DIVIDE reprezinta numele procedurii care realizeaza impartirea secventei in subsecventele si , furnizand valoarea m;

COMBIN reprezinta numele procedurii care realizeaza combinarea rezultatelor r₁ si r₂ ale prelucrarii subsecventelor , , furnizand rezultatul r al prelucrarii secventei .

Procedura se apeleaza prin DIVIMP(1, n, r).

Metoda divide et impera se poate reprezenta sub forma unui arbore binar plin, in care fiecarei secvente , i se asociaza un nod etichetat cu (p, q) in modul urmator:

nodul radacina este etichetat (1, n);

succesorii nodului (p, q) sunt etichetati (p, m) si (m+1, q);

nodurile terminale sunt etichetate (p, q) cu q - p l.

Cazul general se refera la situatia in care o problema de dimensiune n, notata P(n), este impartita in s subprobleme de dimensiune n / n₀, notate P₁(n/n₀), . , P_s(n/n₀).

Daca se noteza cu T(n) timpul cerut de prelucrarea unei probleme de dimensiune n, atunci avem

unde t₀ este o constanta strict pozitiva si t(n) este timpul necesar combinarii rezultatelor subproblemelor P₁(n/n₀),., P_s(n/n₀).

Studiem urmatoarele cazuri:

Cazul 1 s = 2, n₀ = 2.

In acest caz avem

Teorema 4.3

Daca t(n) = cn cu constanta c > 0, atunci T(n) = O(n log₂n).

Demonstratie

Daca n = 2^k > l, atunci se arata prin inductie dupa i ca

T(n) = T(2^k) = 2ⁱ T(2^{k - i}) + c 2^k i , 1 i < k

Pentru i = 1 se obtine

T(n) = T(2^k) = 2 T(2^{k - 1}) + c 2^k

care este adevarata.

Se presupune ca este adevarata relatia

T(n) = T(2^k) = 2ⁱ T(2^{k - i}) + c 2^k i

si sa demonstram ca

T(n) = T(2^k) = 2ⁱ⁺¹ T(2^{k - i - 1}) + c 2^k (i+1)

Avem

2ⁱ⁺¹ T(2^k-i-1) + c 2^k (i+1) = 2 2ⁱ T(2^k-1-i) + 2 c 2^{k - 1} i + c 2^k =

(2ⁱ T(2^k-1-i) + c 2^{k -1} i) + c 2^k = 2 T(2^k-1) + c 2^k = T(2^k) = T(n).

Consideram k_o I N, astfel incat . Evident ca avem k₀ < k si luam i = k - k₀. De asemenea, se tine cont ca , k - k₀ < k, . Rezulta:

Deci T(n) = O(n log₂n)

Daca 2^k < n < 2^k+1, atunci n se majoreaza la 2^k+1

Cazul 2 s > 2, n₀ = 2

Exista probleme care se incadreaza in acest caz. De exemplu, inmultirea a doua numere a si b fiecare cu n cifre binare. Daca n este par, atunci a si b se pot scrie sub forma a = a₁ 2^n/2 + a₂ si b = b₁ 2^n/2 + b₂ cu a₁, a₂, b₁, b₂, numere cu n / 2 biti. Avem a b = a₁b₁2ⁿ + (a₁b₂ + a₂b₁) 2^n/2 + a₂b₂ = c₁2ⁿ + (c₃c₄ - c₁ - c₂) 2^n/2 + c₂, unde c₁ = a₁b₁, c₂ = a₂b₂, c₃ = a₁+ a₂, c₄ = b₁+ b₂. Deci, pentru a b sunt necesare trei inmultiri (c₁ = a₁b₁, c₂ = a₂b₂, c₃c₄) de doua numere de cậte n/2 biti. In acest exemplu avem s = 3, n₀ = 2.

In acest caz T(n) este :

Teorema 4.4

Daca t(n) = c n, cu constanta c > 0, atunci

Demonstratie

Daca n = 2^k > l, atunci se arata prin inductie dupa i ca :

T(n) = T(2^k) = sⁱ T(2^k-i) + c 2^k ( (s/2 )^i-1 +.+ s/2 + 1), 1 ≤ i < k

Pentru i = 1 se obtine :

T(n) = T(2^k) = s T(2^k-1) + c2^k

care este adevarata.

Presupunem adevarata relatia :

T(n) = T(2^k) = sⁱ T(2^k-i) + c 2^k ((s/2 )^i-1 + . + s/2 + 1)

si sa demonstram ca :

T(n) = T(2^k) = sⁱ⁺¹ T(2^k-i-1) + c 2^k ((s/2 )ⁱ +.+ s/2 + 1)

Avem

sⁱ⁺¹ T(2^k-i-1) + c 2^k ((s/2)ⁱ +.+ s/2 +1) =

s sⁱ T(2^k-1-i) + s c 2^k-1 ((s/2)^i-1 +.+ s/2 +1) + c 2^k =

s(sⁱ T(2^k-1-i) + c 2^k-1((s/2)^i-1 +.+ s/2 +1)) +c 2^k =

s T(2^k-1) + c 2^k = T(2^k) = T(n)

Consideram k₀ I N astfel incật . Evident ca avem k₀ < k si luam i = k-k₀. De asemenea, se tine cont ca , k - k₀ < k, . Rezulta:

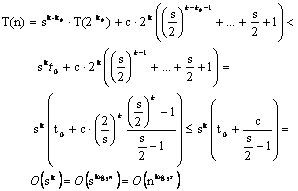
Daca 2^k < n < 2^{k +1} atunci n se majoreaza la 2^k+1.

Cazul 3 s > 2, n₀ > 2

In acest caz avem :

Teorema 4.5

Daca t(n) = c n cu constanta c > 0, atunci

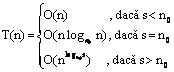
Demonstratie

Cazurile s = n₀ si s > n₀ se trateaza la fel ca in teorema 4.5, respectiv teorema 4.6. Pentru cazul s < n₀ se considera n = n₀^k > l si se arata prin inductie dupa i ca in teorema 4.6, ca

T(n) = T(n₀^k) = sⁱ T(n₀^k-i) + c n₀^k ((s / n₀)^i-1 + . + s/n₀ +1), 1 ≤ i < k

Cosideram k₀ IN astfel incật . Rezulta:

Daca n₀^k < n < n₀^k+1 atunci n se majoreaza la n₀^k+1.

Probleme rezolvate

Problema DI1

Sa se determine cel mai mic element dintr-un sir de numere reale A = (a₁,.,a_m).

Aplicam metoda divide et impera. In acest caz, m = (p+q)/2 si consideram problema rezolvabila direct, daca numarul de elemente din secventa este cel mult 2, deci q - p 1. Pentru n=16, arborele binar plin atasat este prezentat in figura 4.6.

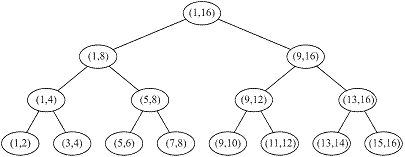
Figura 4.5

Programul in pseudocod este urmatorul:

FUNCTION MIN (A, p, q);

BEGIN

IF q - p l THEN

IF A(p) < A(q)

THEN MIN := A(p)

ELSE MIN := A(q)

ENDIF;

ELSE BEGIN

m := (p + q) / 2

r₁ := MIN(A, p, m);

r₂ := MIN(A, m+1, q);

IF r₁ < r₂

THEN MIN := r₁

ELSE MIN := r₂

ENDIF;

END;

ENDIF;

END;

PROGRAMUL MINDIVIMP;

BEGIN

ARRAY A(n);

READ(n, A);

WRITE('MINIM=', MIN(A, 1, n));

END.

Codul sursa al programului este:

#include<stdio.h>

int min(int x, int y)

int minim(int a[20], int p, int q)

void main()

printf('Minimul din sir este: %dn',minim(a, 1, n));