Modele in spatiul starilor (tip I-S-E)

Modele in spatiul starilor (tip I-S-E)

Sistemele continue si sistemele discrete au modelele de forma

,

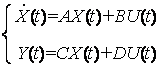respectiv

.

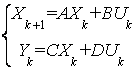Modelul (tip obiect) in spatiul starilor ('state space') al unui sistem continuu se construieste cu ajutorul functiei ss, pe baza matricelor A, B, C, D, astfel:

sss = ss (A,B,C,D);

Daca D este matricea zero, argumentul D poate fi inlocuit in functia ss cu scalarul 0. Sistemul construit prin comanda

sss=ss(D)

este de ordinul zero (fara dinamica), cu ecuatia Y=DU.

Modelul unui sistem discret se construieste tot cu ajutorul functiei ss, pe baza matricelor A, B, C, D si a perioadei de esantionare T, astfel:

sss =ss (A,B,C,D,T);

Modelul construit prin comanda sss=ss(D) este de ordinul zero, cu ecuatia Y_k=DU_k.

Proprietatile modelului sss pot fi afisate cu comanda

get(sss);

Daca sistemul sss este multivariabil, cu comanda

s1=sss(i,j);

se extrage subsistemul monovariabil cu intrarea j si iesirea i.

Din modelul sss se pot extrage parametrii matriceali A, B, C, D, fie cu ajutorul functiei:

[A,B,C,D]=ssdata(sss) ;

fie prin referire directa la proprietatile obiectului model:

A=sss.a; B =sss.b; C=sss.c; D=sss.d; (T=sss.ts;)

Ultima cale permite, de asemenea, modificarea proprietatilor modelului sss

sss.a=A1; sss.b=B1; sss.c=C1; sss.d=D1; (sss.ts=T;)

sau chiar

sss.a(i,j)=a1; sss.b(i,j)=b1; sss.c(i,j)=c1; sss.d(i,j)=d1;

n

Pentru obtinerea sistemului S₁(A₁,B₁,C₁,D₁) echivalent cu S(A,B,C,D), astfel incat X₁=TX (T=S^-1), se utilizeaza functia:

sss1 = ss2ss(sss,T);

iar pentru aducerea sistemului S la o anumita forma canonica S_c (A _c,B _c,C _c,D _c), se utilizeaza functia:

[sssc,T] = canon(sss,'type');

in care 'type' poate fi 'mod' (forma modala) sau 'com' (forma companion). In forma companion, matricea A are ultima coloana formata din coeficientii polinomului caracteristic al matricei A.

Argumentul de iesire T este matricea de transformare, egala cu inversa matricei S, adica T = S^-1.