Rezolvarea ecuatiilor diferentiale

Rezolvarea ecuatiilor diferentiale

MATLAB-ul dispune de metode si functii care pot rezolva problema conditiilor initiale (Cauchy) ale sistemelor de ecuatii diferentiale ordinare (ODE - Ordinary Differential Equations).

In tabelul urmator sunt prezentate succint cateva din aceste functii.

Observatie: La ecuatiile diferentiale ordinare de tip stiff (rigide) solutiile pot avea variatii foarte rapide in timp in raport cu intervalul de timp de integrare si este necesara folosirea unor pasi de integrare foarte mici, ceea ce nu mai este indicat la ecuatiile nonstiff.

Exemplu de rezolvare: ecuatia van der Pol

Ecuatia van der Pol este un exemplu clasic de ecuatie diferentiala:

unde > 0 este un parametru scalar.

Pentru implementarea algoritmului de rezolvare este necesara rescrierea ecuatiei de ordinul 2 ca un sistem de doua ecuatii diferentiale de ordinul 1. Pentru aceasta se introduce variabila y₂ care este derivata in raport cu timpul a variabilei y₁ . Vom avea

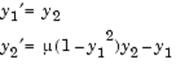
Pentru a reprezenta in MATLAB acest sistem de ODE in scopul gasirii solutiilor, trebuie scris in primul rand un fisier care descrie sistemul (un fisier de tip function). Un fisier ODE accepta cel putin doua argumente, t si y.

Pentru ecuatia van der Pol cu = 1, fisierul este urmatorul (y₁ si y₂ devin y(1) si y(2)):

function dy = vdp1(t,y)

dy = [y(2); (1-y(1)^2)*y(2)-y(1)];

La pasul urmator, dupa ce sistemul de ecuatii a fost scris, se poate utiliza una din metodele de rezolvare prezentate in tabelul anterior. Trebuie furnizat un interval de timp pentru care se doreste calculul solutiilor si bineinteles conditiile initiale.

Pentru exemplul van der Pol, se poate apela la ode45. Daca intervalul de timp este [0 20] iar conditiile initiale y(1)=2 si y(2)=0 vom avea

[t,y] = ode45('vdp1',[0 20],[2; 0]);

Iesirea [t,y] este un vector coloana care contine vectorul timp t si solutia de tip tablou y. Fiecare linie din y corespunde unui element (moment) din vectorul timp.

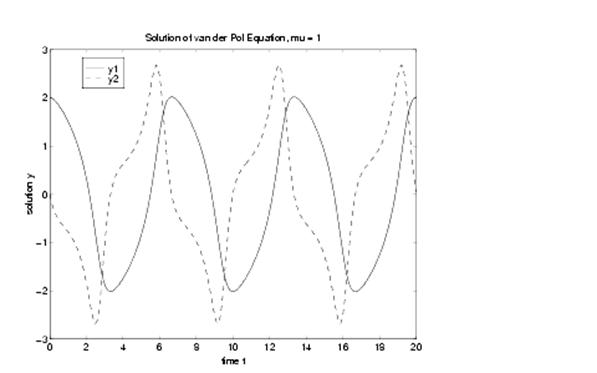
Pentru trasarea graficului cu solutia se foloseste comanda plot:

plot(t,y(:,1),'-',t,y(:,2),'- -')

title('Solution of van der Pol Equation, mu = 1');

xlabel('time t');

ylabel('solution y');

legend('y1','y2')

Se obtine urmatorul grafic care contine evolutiile celor doua componente ale solutiei in timp:

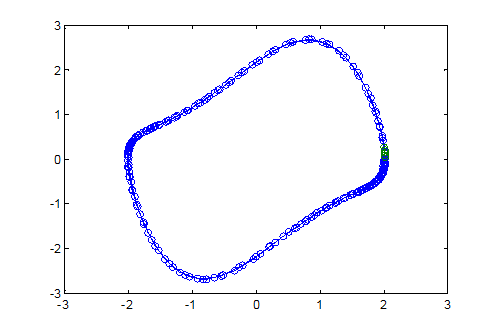
Daca se doreste si trasarea planului fazelor se pot folosi liniile de comanda:

options=odeset('OutputFcn','odephas2');

[t,y] = ode45('vdp1',[0 20],[2; 0],options);

si obtinem planul fazelor (este vorba de trasarea componentei y(1) versus componenta y(2)):