Control solar.

Documentare si propuneri pentru norme

CBD-17-F.  Calculul luminii naturale in locuinte

Murdoch Galbreath

O iluminare adecvata este esentiala in locuinte si, pentru a o obtine, cea mai buna metoda consta in folosirea corespunzatoare a luminii naturale de zi. Ne propunem sa dam, in prezentul Digeste, o dare de seama a cunostiintelor de care dispunem in cea de priveste felul cum se poate capta in mod eficace lumina naturala si sa descriem pe scurt cateva dintre cele mai simple tehnici.

Un mare numar de interioare isi obtin cea mai mare parte a iluminarii naturale gratie experientei ahitecilor care le-au conceput. Arhitectura georgiana a permis obtinerea unor excelente iluminari interioare datorita ferestrelor sale inalte si inguste care faciliteaza penetrarea luminii zilei, a mulurilor care ajutau la creearea unei treceri gradate de la lumina exterioara la cea interioara fara contraste jenante. In urma progreselor tehnice realizate in constructii si in amenajarile de interior, acum este posbila relizarea unor localuri confortabile chiar si intr-o cladire fara ferestre sau intr-o casa de sticla. Este deci normala cautarea in sensul obtinerii unei cunoasteri sporite pe subiectul naturii si functionarii luminii naturale a zilei ca mijloc de iluminare interioara.

In lume, au fost efectuate numeroase cercetari pe subiectul iluminarii naturale si al punerii la punct a unor metode de anticipare pentru ca arhitectii sa poata dispune de o larga paleta de sisteme ce le pot perminte prezicerea, cu o precizie destul de mare, a calitatii si cantitatii iluminarii naturale interioare. Un comitet al Comisiei internationale pentru iluminare pregateste in prezent un manual international care va defini principiile de baza si va compara diversele metode folosite pentru calcularea iluminarii de zi. Acest manual va permite gruparea intr-o singura publicatie a tuturor informatiilor necesare calcularii luminii naturale din locuinte.

Scopul, care consista in anticiparea iluminarii naturale, este foarte dificil de atins, ca urmare a naturii schimbatoare a sursei de lumina. Exista doua stadii in planificarea iluminarii de zi: 1) studierea meteorologica a cantitatii de lumina ce vine de la soare si a claritatii cerului ce este analizata intr-un loc neobturat si 2) determinarea mijloacelor prin care cantitatea dorita de lumina poate ajunge intr-un amplasament interior determinat.

Claritatea cerului

Estimarile claritatii cerului sunt bazate pe date adunate la intevale regulate de-a lungul unui anumit numar de ani. Doua conditii ale cerului, pe care le consideram tipice, sunt in general folosite ca baza de calcul. Acestea sunt:

cerul complet acoperit

cerul degajat, lumina soarelui fiind directa

Cer complet acoperit

Repartizarea claritatii unui cer acoperit nu este uniforma. Ea este in general foarte luminoasa la zenit si foarte intunecata la orizont si in general nu este afectata de pozitia soarelui. Observatiile asupra claritatii cerului facute de Moon si Spencer in Statele Unite au condus la punerea la punct a unei formule ce permite descrierea cerului acoperit:

Observatii efectuate in diferite parti ale lumii au sevit la confirmare utilitatii formulei, cel putin in zonele tmperate, si "cerul lui Moon si Spencer' a fost adoptat la scara internationala de catre C.I.E. drept cer acoperit standard. Repartizarea luminii este conformata astfel incat limpezimea la orizont corespunde aproximativ unei treimi din cea de la zenit si unei jumatati din claritatea medie a cerului.

Chiar daca reparizarea luiminii intr-un cer acoperit este in general conforma modelului standard, nivelul mediu de iluminare variaza in functie de climatul local. Iluminarea medie provenind dintr-un cer acoperit este in principiu cantitatea de lumina ce cade pe un plan orizontal intr-un loc neobstructionat. Alegerea valorilor de calcul potrivite poate fi determinata plecand de la datele meteorologice culese local.

In Canada, exista trei statii meteorologice care masoara iluminarea directa la intervale regulate; iluminarea totala provenita de la cer si soare pe un plan orizontal e inregistrata din ora in ora la Toronto, Scarborough si Ottawa. In plus, in tara exista aproximativ 20 de statii unde sunt inregistrate radiatiile totale. O conversie aproximativa a unitatilor de radiatie in unitati de iluminare ce convin conditiilor cerului acoperit poate fi facuta presupunand ca un gram calorie/centimetru patrat/secunda corespunde la 7000 lumeni/picior patrat. Aceasta valoare a fost folosita in alte tari cu scopul de a obtine informatii utile in ceea ce priveste calcularea iluminarii si pentru a completa releveele directe de iluminare. Valoarea cea mai mica inregistrata nu poate totusi fi folosita la calculele finale si un compromis trebuie acceptat, asemanator celui pe care il folosim pentru a calcula incalzirea de iarna.

In Australia valorile de calcul au fost stabilite pentru principalele orase pornind de la nivelul intensitatii luminoase care va fi depasit de-a lungul a 90% din orele lumina ale zilei, adica de la ora 8 dimineata pana la ora 4 dupa amiaza. Aceasta pare o metoda buna, cu toate ca pentru anumite tipuri de ocupare ar fi potrivita o alta perioada a zilei. Valorile de calcul recomandate pentru conditiile din Australia variaza intre 350 lumeni/picior patrat la Hobart si 1100 lumeni/picior patrat la Darwin. In Marea Britanie, unde climatul este oceanic, valoarea de 500 lumeni/picior patrat serveste drept baza normelor bitanice in materie de lumina de zi.

Variatiile de clima ce se produc in Canada pot face loc unei intrege game de valori de calcul pentru a raspunde nevoilor fiecarei regiuni. Valorile publicate in Monthly Radiation Summaries Service, buletinul meteorologic al ministerului ontarian al transporturilor, pot servi drept baza pentru norma canadiana.

Cer degajat, lumina soarelui fiind directa

Pentru a tine cont in calcule de conditiile de cer degajat si de iluminare directa a soarelui sunt necesare informatii nu numai in ceea ce priveste lumina care cade pe un plan orizontal, dar si privind lumina pe planurile verticale si pe planurile perpendiculare pe directia razelor de soare. La ora actuala exista putine inregistrari de o asemenea natura in Canada, cu toate ca la Ottawa, sunt facute masuratori pe o baza regulata in ceea ce priveste radiatiile totale ce ajung pe suprafete verticale corespunzand principalelor puncte ale busolei. Tabele de iluminare de zi valabile pentru Statele Unite sunt incluse in 'Recommended Practice of Daylighting' publicata de catre l'Illuminating Engineering Society. Informatiile par a fi de o natura mai degraba generala. Iluminarea solara este data in functie de latitudine si este putin probabil ca ar putea conveni conditiilor canadiene.

Metoda factorului luminii zilei

Atunci cand facem planurile unei case in care vrem sa profitam de lumina naturala trebuie sa determinam masura in care lumina disponibila la exterior poate atinge un amplasament determinat in interior. "Factorul de lumina a zilei" folosit ca norma in Europa este o masurare a iluminarii prin intensitatea luminii de zi intr-un punct. Ea este exprimata prin raportare la iluminarea pe un plan dat si la iluminarea exterioara simultana pe un plan intr-un loc fara obstacole. Spre exemplu, daca iluminarea interioara este de 10 lumeni/ picior patrat si iluminarea exterioara pe un plan orizontal de 500 lumeni/picior patrat factorul luminii zilei este de 10/500 sau 2%.

Factorul luminii zilei poate fi descompus dupa cum urmeaza:

Factorul luminii zilei = Componenta cerului + Componenta reflectata externa + Componenta reflectata interna.

Componenta zisa Cer este masura luminii directe venite de la cer si care atinge punctul interior considerat; tabelele si hartile publicate putand fi folosite pentru a obine aceasta valoare. Una dintre aceste harti relativ usor de folosit si in mod particular potrivita pentru calculul preliminar al unei cladiri este cea pe care o gasim in Simplified Daylight Tables publicate in 1958 de catre Departamentul cercetarilor stiintifice si industriale al Marii Bitanii. Tabelele sunt in asa fel dispuse incat arata asa zisa proportie de cer vizibil dintr-un punct pentru care factorul zilei este calculat si au fost modificate pentru a tine cont de efectul unui cer acoperit si de reducerea transmiterii luminii cauzate de un vitraj simplu. Alte corectii putand fi facute pentru cazul vitrajelor duble si pentru efectul stratului de mizerie de pe sticla. Componenta reflectata externa este masura luminii care atinge punctul dupa ce este reflectata de suprafete exterioare cum ar fi cladirile din proximitate care probabil obstructioneaza o parte din lumina directa ce provine de le cer. Procedura ce trebuie urmata este asemanatoare celei folosite in calculul componentei cerului. Zona din zidul opus asa cum o vedem din punctl considerat este obtinuta si multiplicata cu o valoare data claritatii suprafetei zidului reflectant. In general presupunem aceasta valoare ca fiind a zecea parte din limpezimea medie a cerului.

Componenta reflectata interna este cantitatea de lumina ce atinge planul de lucru dupa reflectarea pe pereti, prdoseala, plafonul si acoperis. In numeroasa cazri aceasta componenta poate constitui o proportie importanta a luminii totale disponibile. Marimea componentei reflectate interne este stablita luand in consideratie factorul mediu de reflexie al suprafetelor interioare si dimensiunea incaperii si a ferestrelor. Simplified Daylight Tables dau valori aplicabile factorului de reflexie al materialelor de constructii ordinare si un tabel care poate fi folosit pentru estimarea valorii componentei interne reflectate in incaperile rectangulare.

Metoda lumen

In Statele Unite, mai ales in cursul ultimilor zece ani, numeroase studii au fost consacrate problemei planurilor stabilite in functie de un cer degajat. A rezultat astfel metoda lumen de calcul care a fost conceputa pe baza celei folosite in calculul iluminarii artificiale. Cantitatea de lumina ce cade pe o supafata unei ferestre si povine de la soare si cer si lumina reflectata de catre sol si alte suprafete exterioare, este calculata si multplicata cu un coeficient propriu factorului de transmisie al ferestrei si reflexiilor pe planul de lucru, ce provin de la suprafetele interioare. tre et aux rflexions sur le plan de travail en provenance des surfaces intrieures. Princiiile sunt foarte asemanatoare celor care sunt folosite in calculrea factorului de zi dar scopul acestei metode este cantitatea de lumina obtinuta in amplasamentul dorit, exprimata in unitati de intenstate luminoasa.

O brosura intitulata Predicting Daylight as Interior Illumination si pregatita de catre cercetatorii Universitatii Southern Methodist contin o serie de harti si tabele ce pot fi utilizate pentru a determin iluminarea interioara in puncte situate in incaperi simple, rectangulare si iluminare dintr-o parte. Valorile obtinute sunt limitate la trei puncte din incapere pentru simplificarea calculelor. Punctele sunt situate la 5 picioare fata de centrul zidului ferestrei, 5 picioare fata de zidl de fund si in centrul incaperii. Aceasta metode este putin mai restrictiva decat metoda factorului zilei care permite calcularea oricarui punct al camerei. Principalul sau inconvenient pentru Canada pare a fi raritatea atelor sigure inregistrate in ceea ce priveste claritatea cerului in conditiile canadiene. Valorile claritatii cerului pentru Statele Unite, ce se gasesc in brosura, pot fi folosite pentru compararea eficacitatii relative a diferitelor tipuri de cladiri fara a se preocupa prea mult de valorile absolute. Metoda lumen poate fi folosita pentru a obtine informatii despre lumina naturala provenita de la cerul acoperit si degajat.

Intensitatea iluminarii interioare

Alegerea unei intensitati potrivite a luminarii interioare depinde de felul activitatii care va fi efectuata in incaperea considerata. Valorile de iluminare minima pentru o intreaga serie de activitati sunt enumerate in Lighting Handbook publicata de catre luminating Engineering Society. In cele mai multe cazuri aceste valori sunt mult ai ridicate decat vechile valori recomandate si ele sunt rezultatul unui studiu all lui H. R. Blackwell in ceea ce priveste iluminarea in functie de eficacitatea vizuala. Este de doit ca lumina dintr-o camera sa nu cada sub intensitatea recomandata, mai ales ca in inumite cazuri valoarea minima se poate dovedi insuficienta. De exemplu in cazul in care contrastul intre o activitate si anturajul sau este mult prea mare, cum se poate intampla atunci cand o fereastra este in campul vizual, ochiul se adapteaza la lumina predominanta si obiectele mai putin stralucitoare pot fi dificil de vazut. Folosind una dintre metodele de analiza a luminii zilei este posibila estimarea claritatii relative a diferitelor suprafete ale unei incaperi si realizarea corectiilor necesare. Lighting Handbook al Illuminating Engineering Society contine recomandari cu privire la raportul maxim care ar trebui sa existe intre o claritate de lucru sii o claritate de anturaj pentru a obtine conditii cat mai confortabile. Valorile de mai jos se aplica scolilor si birourilor unde aceste conditii sunt cu atat mai necesare:

Intre zona de lucru si anturajul adiacent: 1 la 1/3

Intre zona de lucru si suprafetele indepartate destul de intunecate: 1 la 1/10

Intre zona de lucru si suprafetele indepartate destul de luminoase: 1 la 10

Intre fereastra si suprafetele adiacente: 20 la 1

Oriunde in interiorul campului vizual normal: 40 la 1

Aceste valori sunt recomandate ca maxime; reducerea lor este in general de dorit.

Principala sursa e orbire este lumina directa asoarelui, iar aceasta poate fi scazuta cu ajutorul a numeroase dispozitive ce se folosesc in prezent si care prodic umbra. Un cer senin fara lumina directa a soarelui este arareori de o asemenea luminozitate incat sa poata cauza conditii inconfortaile, dar lumina soarelui reflectata de catre ziduri adiacente si pardoseli poate fi foarte dezagreabila. Suprafata interioara in culori deschise permite o distribuire uniforma a luminii in incapere deoarece aceste suprafe reflecta mai bine lumina catre punctele cele mai indepartate de fereastra. Reflexia in planseu contribuie deasemenea la iluminarea partii din spate a unei incaperi deoarece lumina directa ce cade pe planseu este reflectata catre plafon si catre alte suprafete interioare. O marire a zonei de ferestre sub planul de lucru nu afecteaza omponenta directa dar poate contribui substantial la lumina reflectata.

Tehnicile folosite pentru calcularea luminii naturale nu sunt foarte diferite de cele pe care le gasim in domeniile conexe construirii caselor. Ele pot fi foarte utilizate pentru armonizarea tipului de fereastra climaturilor regionale si pentru a extrage tot ceea ce se poate din lumina naturala, una dintre resursele noastre naturale. Metodele descrise pot ajuta la rezolvarea celor mai simple probleme de calcul al luminii zilei. Exista totusi tehnici mult mai avansate. O bibliografie completa a studiilor relative la lumina naturale eset inclusa in Recommended Practice of Daylighting.

Bibliografie

Moon, P. and D. E. Spencer. Illumination from a Non-Uniform Sky. Illuminating Engineering, Vol. 37, p. 707-726, 1942.

Monthly Radiation Summaries. Meteorological Branch, Department of Transport, Toronto, Canada.

Recommended Practice of Daylighting. Reprint from 'Illuminating Engineering', Vol. 45, No. 2, February 1950.

Hopkinson, R. G., J. Longmore and A. M. Graham. Simplified Daylight Tables. National Building Studies, Special Report No. 26, London, 1958.

Predicting Daylight as Interior Illumination. Libbey-Owens-Ford Glass Co., Toledo, Ohio, 1960.

IES Lighting Handbook; the Standard Lighting Guide, 3rd Edition 1959. Illuminating Engineering Society, New York, 1959.

Blackwell, H. R. Development and Use of Quantitative Method for Specification of Interior Illumination Levels on the Basis of Performance Data. Illuminating Engineering, Vol. 54, No. 6, p. 317-53, June 1959.

Publicat la origine in ianuarie 1963

Recomandari : Ambianta luminoasa

Automatizarea si informatizarea are ca efect multiplicarea numarului de posturi de lucru echipate cu un calculator, de fapt vederea este foarte solicitata. Pe de alta parte, numarul de ore de lucru, fie noaptea fie in localuri lipsite de lumina naturala, este in continua crestere.

Studierea vizibilitatii si conditiilor de iluminare in care sunt plasati operatorii este foarte importanta pentru conceperea unor amenajaamente care sa limiteze si sa reduca pe cat posibil sarcina vizuala si deci riscul de dezvoltare a unor patologii.

Fie ea naturala sau artificiala lumina creeaza o legatura intre om si mediul sau inconjurator, prin urmare trebuie avuta o grija deosebita in alegerea modului de iluminare, mai ales in spatiile de lucru. Acesta trebuie sa fie adaptat imperativelor cantitative si calitative ale confortului visual.

Confortul vizual presupune un echilibru al luminozitatilor in interiorul campului visual. Regula iluminarii maxime a zonei centrale a campului visual si descresterii treptate a luminozitatii catre periferie, nu poate fi intotdeauna aplicata in cazul activitatilor ce se desfasoara in fata unui ecran.

In aceasta situatie operatorul trebie sa-si desfasoare munca in doua conditii diferite:

• citirea documentelor manuscris imprimate in contrast pozitiv (caractere inchise pe fond deschis)
• citirea pe ecran in contrast negativ (caractere deschise pe fond intunecat)

Aceste doua conditii solicita functiuni vizuale diferite: acomodarea si adaptrea cristalinului.

Cand se face trecerea de la vedereade aproape la cea de departe, imaginea clara se formeaza in spatele retinei, cele doua imagini converg printr-o contractie a muschiului cristalinului si diametrul pupilei se micsoreaza.

In cazul unei actvitati la ecran, distantele foarte diferite intre cristalin - ecran si cristalin - document solicitand mult prea des functia de acomodare contribuie la oboseala vizuala.

Adaptrea este a doua functie a vederii care contribuie la claritatea imaginii prin dilatare sau nu a pupilei pentru a mari sau micsora cantitatea de lumina ce ajunge la retina. Si in acest adaptarile neincetate cauzeaza oboseala vizuala.

Iluminarea trebuie sa asigure o perceptie vizuala pentru toate activittile efectuate de catre un operator. Nivelul de iluminare, efectul de orbire contrastele luminozitatilor si culorile sunt tot atatia factori de care trebuie tinut cont in momentul amenajarii posturilor de lucru.

O buna iluminare trebuie sa realizeze o coerenta optimala intre lumina naturala si cea artificiala.

a) Lumina naturala

Lumina naturala are efecte benefice asupra sanatatii si psihologiei finitei umane: ea ritmeaza functiile neurovegetative, tonifica, evita riscurile de claustrofobie.Perceperea ciclului diurn - nocturn contribuie la mentinerea echilibrului general.

• Factorul "lumina de zi' se stabileste functie de indicele vitrajului, adica raportul suprafata vitrata : suprafata planseului, trebuie sa fie cuprins intre 20 si 30 % pentru a permite un nivel de iluminare de 250 lucsi pentru 5000 lucsi la exterior.

• Deperditiile luminoase sunt legate de fiecare tip de fereastra si vitraj: grosime a ramei si transparenta a suprafetei vitrate.

• Posibilitatile de vederi catre exterior permit cristalinului focalizarea pe un orizont indepartat    favorizand astfel pozitii de odihna. Pe de alta parte perceperea ciclului diurn - nocturn contribuie la mentinerea echilibrului general al fiintei umane.

Nivelul de iluminare este fluxul luminos primit de catre o suprafata (este exprimat in lucsi si masurat cu ajutorul unui luxometru)

Dincolo de 6 metri distanta fata de deschidere, iluminarea obtinuta pentru un post de lucru este insuficient si aceasta zona trebuie considerata drept oarba. Masurarea nivelului de iluminare se face la un metru de sol dupa un caroiaj.

Tabelul de mai jos furnizeaza nivelul de iluminare in functie de locul activitatii.

Nivelul de iluminare in functie de locurile de activitate

Stapanirea luminii artificiale poate varia considerabil dupa ora din zi, vreme, lumina naturala, anotimp. Orientarea si insorirea sunt de aceea determinante.

O fatada de culoare deschisa situata vis-a-vis de o deschidere aduce un aport considerabil de lumina. De fiecare data cand indicele vitrajului deschiderilor expuse insoririi este important trebuie pusa problema aportului termic.

Prafuirea si imbatranirea reduc notabil eficacitatea surselor.

b)  Lumina artificiala

repartizarea luminii artificiale se face in doua feluri :

• Iluminare directa : cel putin 90% din lumina este emisa de sus in jos. Contrastele sunt violente si umbrele foarte marcate. Exista foarteputine reflexii pe plafon si pereti.
• iluminare indirecta : cel putin 90 % din lumina este dirijata de jos in sus. Iluminarea este difuza cu o intensitate ce depinde de puterea de reflexive a plafonului.
• Lminozitatea surselor trebuie sa fie inferioara valorii de 100 cd/m2 pentru o activitate ce presupune munca pe ecran.

Iensitatea luminoasa este cantitatea de lumina reflectata de catre o suprafata si rprimita de catre cristalin; ea se exprima in candele/ metru patrat; prea puternica, provoaca senzatia de orbire. Masuram in general luminozitatea obiectului si pe cea a fondului. Aceste masuri se iau cu ajutorul unui aparat numit luxometru.

Echilibrul luminozitatilor se bazeaza pe o limitare a raporturilor de luminozitate intre obiectul prcis si suprafetele adiacente si inconjuratoare.

Este recomandabil sa nu se depaseasca:

• un raport de 1 . 3 intre pata si suprafetele adiacente
• un raport de 1 . 10 intre pata si suprafetele cele mai indepartate
• un raport de 20 . 1 intre surse de lumina / vitraje si pata.

Buna repartitie a surselor de lumina depinde pe de o parte de dispoztivul de difuzare a luminii adoptat si pe de alta de factorii de reflexie ai diferitelor suprafete ale localului.

Coeficienti de reflexive in functie de suprafata localului

In general sunt de preferat finisajele mate pentru a evita reflexiile, surse ale senzatiei de orbire.

Recomandari

Document realizat de catre Marit Milon

Generalitati asupra luminii naturale si a luminii polarizate

In sursele termice uzuale, fotonii sunt emisi in urma coliziunii dintre electroni si atomi sau molecule. Acesti atomi sau molecule, sunt adusi astfel in stari de excitatie si de dezexcita imediat, in mod spontan, emitand lumina. Particulele excitate se comporta ca dipoli electrici emitand unde amortizate ale caror faze sunt aleatorii. Oscilatiile se amortizeaza sub efectul radiatiei emise si sunt relansate die mai multe miliarde de ori pe secunda. Vibratiile emise de fiecare data de catre oscilatorii prezenti nu au intre ele nici o relatie de faza si amplitudine si directia lor de polarizare varaza intr-un mod aleatoriu: nu exista azimut privilegiat dupa observatii a caror durata este in mod considerabil mai mare decat durata fiecarui oscialtor. Vibratia luminoasa va prezenta deci o simetrie derevolutie. Daca am putea izola un oscillator si observa radierea sa pe timpul unei durate de ordinal unei miliardimi de secunda, atunci vibratia emisa ar avea o faza, o amplitudine si o directie de polarizare perfect definite. Lumina obtinuta ar fi polarizata. Vom presupune ca lumina naturala poate fi reprezentata printr-o vibratie eliptica a carei faza, amplitudine si directie se schimba de un milliard de ori pe secunda.

O vibratie elliptic apoate fi definite ca suma a doua vibratii perpendiculare, spre exemplu o vibratie OM1 pe directia Ox si o vibratie OM2 pe Oy, defazate una fata de cealalta cu 

 corespunzand avansului de faza al vibratiei OM2 in raport cu vibratia OM1. Vibratia rezultanta este OM = OM1 + OM2. Traiectoria punctului M este o elipsa inscrisa in drptunghiul cu laturile 2a si 2b (figura 1).

Determinarea ecuatiei elipsei: sistemul de ecuatii (1) descrie elipsa sub forma parametrica cu parametrul t.

Plecand de la (1) putem scrie :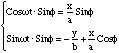

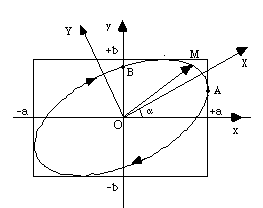
Figura 1 : polarizarea eliptica

Eliminam t radicand la partat si adunand. Gasim astfel ecuatia carteziana a elipsei :

(2)

putem incerca sa gasim directiile OX si OY ale axelor elipsei. Calculul de mai jos permite gasirea lui  deci reperul OXY, in functie de parametrii a, b si  care au servit la definirea initiala a elipsei. Ecuatiile de schimbare de reper se scriu :

x = XCos - YSin y = XSin + YCos

si ecuatia (2) devine :

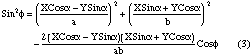
dezvoltand si regrupand termenii, putem pune (3) sub forma :

Sin2 = X2(.) + Y2(.) + XY(.)

Daca ne situam in reperul axelor elipsei, coeficientul termenului XY trebuie sa fie nul :

Ceea ce da : (4) avec

Pentru  = /2 si 3/2, avem Cos = 0 : axele elipsei sunt axele Ox si Oy.

Mai ramane de gasit sensul de rotatie al punctului M pe elipsa din figura 1. Pentru t = 0 avem x = +a si punctul M este in A. Pntru a gasi sensul de rotatie este de ajuns sa calculam derivata in t = 0 :

in t = 0.

Pentru 0 <  , aceasta derivate este negative, rotatia se face in sensul sagetilor indicate in figura 1. Spunem ca polarizarea este eliptica dreapta (cand M este in B, se intoarce imediat catre dreapta).

Pentru <  aceasta derivate este pozitiva, rotatia se efectueaza in sens opus sensului sagetilor din figura 1. Spunem ca polarizarea este eliptica stanga (cand M este in B, se intoarce imediat catre stanga).

Ansamblul rezultatelor este rezumat in figura de mai jos, care descrie starea de polarizare eliptica in functie de  pe intervalul (0,2). Pentru a fixa ideile, am ales > b (dreptunghi dezvoltat pe orizontala)

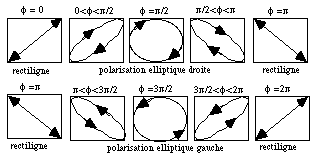
Figura 2 : starea de polarizare in functie de

Cazuri particulare :

1)  = 0 si  =  . vibratia este de polarizare rectilinie.

x/a = y/b pentru  = 0 . M descrie un segment de dreapta de panta b/a.

x/a = -y/b pentru  . M descrie un segment de dreapta de panta -b/a.

2)  =  et  = 3si in plus a = b. Elipsa devine cerc, avem o vibratie de polarizare circulara.

 : polarizare circulara dreapta.

 : polarizare circulara stanga.

3) a = b . daca Cos este non nul, tg2 este infinita dupa (4). Axele elipsei raman la 45. In cazul in care Cos = 0, ecuatia (4) da o forma indeterminate pentru tg2, ceea ce este normal de vreme ce ajungem din nou in cazul 2) al polarizarii circulare.

Concluzii

Admitem ca lumina naturala se constituie ca succesiune de vibratii eliptice a caror forma, orientare si faza se schimba in mod aleatoriu de mai multe miliarde de ori pe secunda. Putem deci considera lumima naturala ca fiind formata din dooua componente de vibratie independente, una urmand axa Ox, cealalta axa Oy :

x = aCos(t+x) si y = bCos(t+y).

Amplitudinile a si b si fazele x si y se schimba des si in mod independent. Acestea sunt vibratii incoerente. Intensitatea luminii naturale este valoarea medie temporala a a2+b2 : I0=<a2>+<b2>. In plus, cele doua componente contribuie in mod egal la intensitatea totale a luminii naturale : Ix = <a2> = Iy = <b2> = I0/2.

Lumina polarizata este constituita dintr-o vibratie ale carei componente pe Ox si Oy au amplitudini a si b constante una fate de cealalta : tg = b/a, deci faze x si y constante una fata de cealalta : y = x + . O vibratie polarizata se va scrie deci :

x = A.Cos.Cos(t + x )

y = A.Sin.Cos(t + x + )

A si x se pot schimba de mai multe miliarde de ori pe secunda, dar  si  raman constante. Spunem ca aceste componente sunt doua vibratii coerente.

PROPAGAREA IN MEDII IZOTROPE

REFLEXIE, REFRACTIE

I) GENERALITATI

In mediile izotrope vom avea et unde  si  sunt marimi scalare. Deci si pe de o parte, si pe de alta, sunt colineare. Mai mult, nu luam in considerare faptul ca undele electromagnetice variaza sinusoidal de-a lungul timpului.

I-A) Medii izolante perfecte (dielectrice fara pierderi)

Medii fara sarcini libere :  = 0

 = 0 (izolant) si  si  reale (fara pierderi) (in general  = 0).

Ecuatiile lui Maxwell se scriu :

De unde deducem ecuatia de propagare :

Solutia in unda plana se scrie in notatie complexa :

avec

Solutia fizica este :

I-B) Medii conductoare si izolante imperfecte (dielectrice cu pierderi)

Medii fara sarcini libere :  = 0 (intr-un mediu conductor, sarcinile libere se echilibreaza cu sarcinile legate in asa fel incat  tinde foarte repede catre zero).

Pentru un conductor,  , 0,  si  reale si in general  = 0.

Pentru un dielectric cu pierderi,  = 0,  = * complex si in general  = 0.

Ecuatiile lui Maxwell se scriu:

pentru un conductor

pentru un dielectric cu pierderi

Daca, in cazul metalului, luam * = -iatunci ecuatia (2') se scrie la fel ca (2') si cele doua sisteme sunt echivalente. Ele sunt deasemenea asemenea primului sistem (dielectric fara pierderi) dar acum cu * complex in loc de  real astfel incat ecuatia undei se scrie :

si solutia in unda plana va face sa intervina un vector de unda complex care verifica ecuatia :

II) REFLEXIE SI REFRACTIE - FORMULELE LUI FRESNEL

Considerand o unda electromagnetica plana ce cade sub incidenta i pe suprfate de separare (ne incarcata) intre doua medii de constante (1, 0) si (2, 0). Fie normalae la aceasta suprafata de separare.

Undele plane satisfac ecuatiile lui Maxwell in cele doua medii. Notam unda incidenta, unda transmisa, unda reflectata. Prin conventie, reperam unda incidenta in reperul Oxyz, unda transmisa in reperul O'x'y'z' si unda reflectata in reperul O'x'y'z' (figura 1 pagina urmatoare). Axele Ox, O'x' et O'x' sunt perpendiculare pe planul de incidenta, toate trei orientate in acelasi sens. Axele Oz, O'z' et O'z' sunt dirijate in lungul razei luminoase si orientate toate trei in acelasi fel fata de sensul de propagare a luminii, aici toate trei in sensul de propagare. Axcele Oy, O'y' et O'y' sunt in planul de incidenta; orientarea respectiva este impusa de catre conditia ca cele trei repere trebuie sa fei repere ortogonale directe.

Avem relatiile : , et . Conditiile de pasaj sunt satisfacute la interfata:

Pentru mediile izolante neincarcate avem  = 0 si = 0. Pentru mediile conductoare putem arata ca = 0 daca conductorul nu este perfect (conductivitate  non infinita).

In toate cazurile este deci de ajuns sa verificam:

si

Figura 1 : repararea undelor incidenta, transmisa et reflectata

Legi ale reflexiei si ale refractiei.

Vectorii , si sunt coplanari (plan de incidenta).

i = i' (in valoare absoluta).

kSini = k'Sinr adica n1Sini = n2Sinr sau Sini = nSinr

cu n = n2 / n1 indice relativ al mediului 2 in raport cu mediul 1.

Formulele lui Fresnel.

Consideram succesiv cazul unei unde incidente polarizate in planul de incidenta EP (EP dirijat dupa Oy) apoi cazul unei unde incidente polarizate perpendicular pe planul de incidente EN (EN dirijat dupa Ox). Formulele lui Fresnel dau coeficientii de reflexie si de transmisie in amplitudine :

Dpendenta lui rP si rN in functie de i pentru n>1 este reprezentata in figura 2.

Figura 2 : dependenta coeficientilor de reflexie rP si rN in functie de unghiul de incidenta i (cazul n>1).

Remarca. In alegerea reperelor pentru descrierea polarizarii intalnim maimulte conventii differite de la lucrare la lucrare. Pentru fasciculul reflectat, doua conventii sunt posibile pentru alegerea reperului O'x'y'z'. Acesta poate fi ales asa cum este indicat in figura 1 si formulele date aici sunt in acest caz valabile. In alte lucrari, mai ales de limba franceza, sensul axei O'z' este inversat. Trebuie deci inversat si sensul axei O'y' pentru ca triedrul ramane direct si prin urmare trebuie schimbat semnul expresiei rP (ecuatia (5) ). In continuare toate rationamentele si calculele vor fi facute respectand conventia din figura 1.

III) LUMINA REFLECTATA PE UN MEDIU DIELECTRIC.

Inlocuind n cu Sini/Sinr, formulele lui Fresnel pot fi scrise :

si (11)

S luam cazul in care cel de-al doilea mediu este mai rece decat primul (n>1). Daca i creste de la 0 la /2, r creste de la 0 la unghiul limita  definit de nSin = Sin(/2) = 1.

Pentru i mic avem i = nr si formulele lui Fresnel devin :

si (a se vedea figura 2)

Atunci cand trecem de la incidenta normala i = 0 l aincidenta razanta i = /2, Sin(i+r) ramane superior lui zero si rN ramane negativ ; in schimb, (i+r) depasind valoarea /2, tg(i+r) isi schimba semnul trecand prin infinit si rP isi schimba deci semnul trecand prin zero. In acest moment, faza vibratiei reflectate sufera o variatie brusca a lui . Ughiul iB pentru care rP este nul este unghiul lui Brewster. Avem deci iB + rB = /2 si tgiB = n.

Daca lumina incidenta este lumina naturala, o putem considera ca fiind formata din doua componente perpendiculare de intensitati egale si fara coerenta de faza. Lumina reflectata va fi si ea formata din doua componente perpendiculare incoerente dar de intensitati inegale in raportul: . Prin urmare, cum in afara de cazul incidentei normale si al incidentei razante pentru care avem egalitate, lumina reflectata va fi partial polarizata perpendicular pe planul de incidenta. Ea devine total polarizata in aceasta directie pentru incidenta lui Brewster.

Daca lumina incidenta este polarizata rectililiniu, directia de polarizare care face unghiul i cu normala l aplanul de incidenta, putem descompune aceasta unda incidenta in doua vibratii ortogonale coerente de aceeasu faza si de amplitudini : EP = E.Sini si EN = E.Cosi (a se vedea figura 3).

Figura 3 : Polarizarea undelor incidenta si reflectata

Vibratia reflectata este rezultanta a doua vibratii rectilinii ortogonale, cerente de aceeasi faza si amplitudini E'P si E'N date de formulele lui Fresnel. Este o vibratie rectilinie care face cu normala la planul de incidenta unghiul r definit de :

IV) LUMINA REFLECTATA PE UN MEDIU METALIC

Avem acum o constanta * complexa si deci un indice n* complex definit de :

 este indicele de refractie ; viteza de faza este v = c/

 este indice de stingere ; unda isi diminueaza amplitudinea pe parcursul propagarii sale. Unda plana uniforma care se propaga intr-un astfel de mediu se scrie:

Cu toate ca n* este complex, putem totusi folosi legile lui Descartes si formulele lui Fresnel cu un unghi de refractie r ' definit de sinusul si cosinusul sau astfel :

este un numar complex si il vom pune :

Atentie, Sinr si Cosr sunt aici numere complexe; r nu este deci in nici un caz un unghi de refractie real. De fapt si sunt, de factor /c, componente perpendiculare la interfata si paralele cu interfata vectorului undei al undei transmise in metal. Acest vector de unda este un vector complex .

Din (14) si (15) rezulta : adica, separand partile reale si imaginare : (16) si (17)

Ecuatiile (16) si (17) arata ca, daca cunoastem p si q pentru o incidenta data, putem deduce  si . In plus, intr-un metal avem in general . Ecuatia (14) se simplifica sub forma :

adicacare inlocuieste ecuatiile (16) si (17). Ramane de aratat cum putem accesa o masura a cantitatilor p et q pentru o incidenta i data.

Amplitudinile vibratiilor reflectate pentru o vibratie incidenta in planul de incidenta EP sau normala la planul de incidenta EN sunt date de formulele lui Fresnel (5) si (7). rP si rN sunt acum numere complexe si . Argumentele P si N ale acestor calitati reprezinta avansurile de faza produse de reflexie. Ele sunt diferite, iar diferenta dintre ele  P - N, care este quasi argumentul numarului complex  = rP / rN, reprezinta avansul de faza al polaritatii reflectate E'P fata de E'N .

Daca lumina incidenta este polarizata rectiliniu la 45 fata de normala la planul de incidente, amplitudiniles incidente EP si EN sunt egale si in faza. Pentru amplitudinile reflectate vom avea:

Vom scrie  sub forma : (20)

unde tg este o cantitate reala pozitiva.

 poate fi exprimat plecand de la formulele lui Fresnel (9) si(10) :

care se transforma folosind (13) si (15) : (21)

Cantitatea  nu este reala decat pentru i = 0 unde avem  = -1 deci  = 

Si pentru i = /2 unde avem  = +1 deci  = 0

Intre aceste doua limite avansul de faza  al E'P in raport cu E'N variaza continuu intre  si 0. Deci pentru orice incidenta diferita de incidenta normala (i = 0) sau de incidenta razanta (i = /2), lumina reflectata va fi polarizata eliptic.

Daca, dupa reflexie, introducem intre cele doua valori componente E'P si E'N o diferenta de faza ', produsa de o lama birefringenta, care compenseaza defazajul  cele doua vibratii sunt aduse la aceeasi faza. Vibratia rezultanta este deci rectilinie in directia  fata de normala la planul de incidenta devreme ce prin definitia lui  (a se vedea fiigura 4). Putem deci determina experimental si  pentru o incidenta i data

Pentru a face legatura intre p si q cautate si si  cunoscute, calculam cantitatea pornind de la relatia (21) in functie de p, q si i si plecand de la (20) in functie de si . Gasim:

Egaland (22) si (23) obtinem rezultatul cautat :

(24) si (25)

Din (18) si (19) deducem  si  :

Daca, in plus, consideram cazul particular  = /2, numim incidenta corespunzatoare incidenta principala iP si unghiul P asociat azimut principal. In aceasta configuratie particulara, relatiile (26) si (27) se simplifica si obtinem :

si

PRODUCEREA SI ANALIZAREA UNEI LUMINI

POLARIZATE

OPTICA CRISTALINA

I)           PRODUCEREA SI ANALIZAREA UNEI POLARIZARI RECTILINII

Lumina polarizata rectilinie se obtine pornind de la lumina naturala, trecand fasciculul luminos printr-un material care absoarbe una din componentele de polarizare ale luminii naturale lasand-o pe cealalta sa treaca. Acest material constituie un polarizator rectiliniu, numit mai simplu polarizator. El se caracterizeaza prin directia sa de polarizare, adica directia vibratiilor pe care le lasa sa treaca.

Cei mai uzuali polarizatori, numiti 'polaroizi', se prezinta sub forma de folii subtiri de plastic. Aceste folii sunt formate din lanturi moleculare lungi (polimeri) dispuse paralel pe o directie data la fabricare. Aceste lanturi polimerice inglobeaza radicali ce contin iod, care pot furniza electroni. Acestia se pot deplasa de-a lungul lanturilor, dar nu si pe o directie perpendiculara. Maretialul astfel constituit este un conductor rezistiv, deci absorbant, pentru polarizare pe directia de aliniere si un izolant transparent pe directia perpendiculara.

Acelasi dispozitiv, numit de aceasa data analizator, permite analizarea luminii incidente polarizate. De fapt, daca printr-un asemenea analizator lasam sa treaca un fascicol de lumina polarizata rectilinie de intensitate 10, intensitatea transmisa va fi It = I0.Cos2 unde  este unghiul dintre directia incidenta de polarizare si directia transmisa de catre analizator. Extinctia totala va fi obtinuta in momentul in care cele doua directii sunt perpendiculare. Putem astfel cunoaste directia polarizarii incidente, cunoscand caracteristicile analizatorului.

II)        MEDII ANIZOTROPE BIREFRIGENTE

Scopul acestui paragraf nu este acela de a prezenta teoria mediilor anizotrope in ansamblul sau, ci de a da cateva elemente de teorie pentru intelegerea imediata a moduluie de functionare a lamelor subtiri birefrigentege.

Intr-un mediu anizotrop, relatia care leaga deramane lineara dar nu mai este scalara, ca in mediile izotrope.  este acum un tensor de rang 2 pe care il vom scrie,

si care, intr-un sistem dat, va fi reprezentat de o matrice 3x3. Avem relatia . In plus, plus, exista un sistem ortogonal particular OXYZ, numit sistem de axe principale, in care este diagonal, cele trei elemente diagonale X, Y si Z fiind pozitive. Definim deasemenea trei indici principale prin : pentru i = X, Y, Z.

1) Daca X = Y = Z este un scalar. Mediul este izotrop.

2) Daca X = Y  Z Mediul este anizotrop uniaxat. OZ se numeste axa optica.

n0 = se numeste indice de ordinar.

ne = se numeste indice extraordinar.

Daca ne > n0 mediul se numeste uniaxat pozitiv.

Daca ne < n0 mediul se numeste uniaxat negativ.

3) Daca X  Y  Z Mediul este anizotrop biaxat.

Atunci cand vrem sa aflam undele electromagnetice plane care se pot propaga intr-un mediu anizotrop dupa o directie de propagare (directia vectorului undei ) data, gasim doua directii privilegiate si pentru vectorul in asa fel incat o unda polarizata (sau ) se propga in mediul anizotrop fara a-si schimba polaritetea. Aceste doua directii se numesc liniile neutre ale lamei. Ele sunt perpendiculare la si perpendiculare intre ele. Unda de polaritate se propaga cu un indice n' si o vitteza de faza c/n', cea de polaritate cu un indice n' si o viteza de faza c/n'.

In afara unui caz exceptional, n' si n' sunt diferiti unul de altul si undele se progaga cu viteze diferite. Din acest motiv, oricare ala polaritate incidenta, diferita de sau , se va modifica in cursul propagarii sale in mediul anizotrop. De fapt, orice polaritate incidenta poate fi descompusa in doua componente, una dupa , iar cealalta dupa , eventual defazate una fata de cealalta. Datorita diferentei dintre n' si n', acest defazaj va evolua in cursul propagarii si isi va schimba cantitatea unde e este grosimea mediului anizotrop traversat. La iesire, cele doua componente pot fi recompuse, dar cum defazajul lor difera fata de cel de la intrare, polaritatea undei va fi modifiata. Spre exemplu, daca vibratia de plecare la intrarea in lama era rectilinie (doua componente in faza), la iesire vibratia va fi eliptica si starea sa exacta de vibratie va fi, in functie de defazajul , asa cum este indicata in diferitele elemente ale figurii 2 din primul capitol.

In general, determinarea liniilor neutre si si a indicilor asociati n' si n' pentru o directie data intr-un material birefrigent este destul de complicata. Ne vom limita la urmatorul caz simplu : un mediu uniaxat (un singur ax optic) si o propagare dupa o directie perpendicular pe aceast ax optic. Este situatia pe care o intalnim atunci cand o lama subtire birefrigenta cu fete paralele, taiata paralel de axa optica, este traversata de un fascicol de lumina sub incidenta normala. In acest caz particular directiile privilegiate (liniile neutre) sunt, in planul perpendicular pe , directia axului optic, de indice n' = ne si directia perpendiculara pe acest ax, de indice n' = n0 (vezi figura 1). Pentru a fixa ideile, luam situatia lui ne > n0 . Directia (axul optic) se va numi atunci axul lent deoarece coerespunde vitezei de propagare celei mai slabe (c/ne < c/n0).

III)     PRODUCEREA SI ANALIZAREA UNEI POLARIZARI ELIPTICE

O lama subtire birefringenta de grosime e si ale carei fate de intrare si iesire sunt paralele cu axa optica introduce, intre vibratiile polarizate dupa cele doua linii neutre ale sale, o diferenta de faza .

Cazurile cele mai interesante sunt cele pentru care avem  (modulo 2) si /2 sau 3/2 (modulo 2).

 (modulo 2), avem o lama semi-unda. Daca vibratia incidenta este rectilinie, vibratia de iesire este la randul ei rectilinie dar pe o directie simetrica fata de cea a vibratiei incidente fata de liniile neutre ale lamei (vezi figura 2)

2) /2 sau 3/2 (modulo 2), avem o lama sfert de unda . Daca vibratia incidenta este eliptica avand axele dupa liniile neutre ale lamei, vibratia de iesire va fi rectilinie. Daca vibratia incidenta este rectilinie, vibratia de iesire va fi eliptica cu axele dupa liniile neutre ale lamei. Pentru a gasi sensul de rotatie al vibratiei eliptice, trebuie stiut care dintre liniile neutre est axa lenta (axa cu indicele cel ma ridicat) si daca lama introduce un defazaj /2 sau 3/2 (modulo 2).

Figura 2 : Efectul unei lame birefringente semi-unda sau sfert de unda asupra unei polarizari incidente. Axa lenta a lamei este intotdeauna verticala..

Producerea unei polarizari eliptice. Plecand de la o vibratie rectilinie, o lama sfert de unda produce o vibratie eliptica ale carei axe sunt dirijate dupa liniile neutre ale lamei (figura 2). De fapt, lama introduce pentru componenta polarizata dupa axa lenta o intarziere de faza (sau 3/2) fata de componenta polarizata dupa axa rapida. In cazul particular in care vibratia incidenta este la 45 de liniile neutre, vibratia la iesire va fi de polaritate circulara (stanga sau dreapta).

Analiza unei vibratii eliptice. O unda electromagnetica de polaritate eliptica, ce traverseaza o lama sfert de unda si ale carei linii neutre sunt orientate dupa axele elipsei, devine la iesire o vibratie rectilinie, ca in figura 2. Un analizator clasic permite caracterizarea imediata a acestei polarizari rectilinii reperand directa sa de vibratie, ceea ce da acces la raportul b/a al celor doua axe ale elipsei.

Remarca : depinde de ; o lama nu este deci un sfert de unda (semi-unda) riguros definita decat pentru un  dat care trebuie precizat. Daca nici o indicatie nu este data, lama trebuie sa fie sfert de unda (sau semi-unda) pentru lungimea de unda medie a spectrului vizibil, moy = 550 nm. Din dependenta lui  in 1/ deducem c adefazajul introdus de catre o lama sfert de unda de acest ti va fi inferior lui /2 pentru  > moy (pentru rosu) si superior lui /2 pentru  < moy (pentru albastru). Aceasta dependenta este putin importanta daca lama are o grosime de moy = /2 dar va avea cu mult mai multa importanta daca lama este de moy = /2 + k cu k intreg , 0.

Orasele si lumina

Este dificil astazi sa ne imaginam un oras fara lumina. Orasele nu folosesc lumina doar pentru a-si ilumina spatiile publice, dar si pentru a pune in evidenta anumite edificii si pentru a-si decora strazile. Astfel anumite reflectoare si becuri dau noaptea un aspect magic cladirilor si strazilor. Acest effect nu poate fi obtinut prin lumina soarelui. Iluminarea artificiala nu dezvaluie decat o parte a operei lasand restul in seama imagiatiei noastre.

Un oras se distinge adesea fata de rural prin lumina pe care o degaja. De fapt, strazile orasului sunt in general mai luminate decat strazile de tara ce traverseaza satele. Avem cu totii in minte imaginea Las Vegasului unde torente de lumina ies din pancartele publicitare si fatadele cladirilor. Acest oras, prin exuberanta stralucirii, vrea poate sa demonstreze ca viata nu se opreste la caderea noptii, sau poate, o alta presupunere, ca orasenilor le este frica de intuneric. Gasim aici unul dintre contrastele existente intre urban si rural. Aceste decoratii luminoase au poate si sensul sarbatorii. De fapt numeroase orase se imbraca in lumina in preajma unor sarbatori, cum este Craciunul, comemorarea unei date de importanta nationala sau a unui carnival.

Perceperea unui loc depinde de lumina. Astfel, un loc intunecat in oras da imediat o senzatie de nesiguranta. In penumbra nu mai reusim sa vedem totul si se instaleaza impresia ca pierdem controlul asupra mediului ce ne inconjoara. Cu toate acestea, daca traversam acelasi loc ziua, nu mai avem neaparat sentimentul de nesiguranta. Putem lua drept exemplu numeroasele parcuri din Geneva. Ziua iluminarea este suficienta pentru a hoinari in linistite, parcurile sunt animate de copii care se joaca sau de catre persoanele care se plimba. Pe cand, soarele odata apus, aceste locuri care au cunoscut viata de-a lungul intregii zile, devin spatii unde nu ne mai simtim tocmai in largul nostrum. Traversati parcul Bastions, o data ziua si o data noaptea, si veti vedea diferenta.

Anumite amenajamente au fost effectuate in oras, si mai ales in piete, pentru a umaniza spatiile. Daca imi permit sa folosesc acest termen, a umaniza, o fac deoarece cred ca omul are nevoie sa se simta in siguranta oriunde merge. Pentru aceasta este necesar ca spatiile, care ii erau ostile, sa devina locuri unde poate sa se simta in largul sau. Sa luam de exemplu piata Volontaires situate in fata uzinei. Inainte de renovarea sa, aceasta piata nu era accesibila pentru toata lumea , acum gasim aici banci si o buna iluminare nocturna. Asta face ca o anume categorie de persone sa dispara sau daca nu, cel putin a devenit mai discreta. Piata a devenit mai primitoare si atunci cand o traversam nu mai avem sentimental ca riscam sa fim agresati in orice moment.

Dupa ce am vazut rolul iluminarii artificiale in oras, vom vedea nuantele luminii naturale. De fapt, lumina naturala, care ajunge intr-un anume loc, variaza in functie de amplasament, conditiile meteo si ora. O piata va fi judecata ca mai calduroasa daca este bine iluminata. Pentru aceasta trebuie ca ea sa ofere un degajament pentru a permite luminii sa intre. Imediat dupa aceasta, trebuie ca lumina sa nu fie difuza ca atunci cand cerul este noros. Si in sfarsit, in timpul zilei, lumina ce ajunge pe pamant este alba, ceea ce intareste aceasta ide de caldura. In poreajma rasaritului sau apusului soarelui lumina are o nuanta de rosu. Atunci cand ea se proiecteaza pe zidurile orasului, atmosfera se schimba si dupa senzatia de caldura vine cea de blandete.

Rosu, roz, galben pal, potocaliu, acestea sunt luminile prezentate la Geneva atunci cand soarele rasare si apune, in spatele micutului Salve si respective, al Crte-ei de l'Aiguillon du Jura (mai mult sau mai putin dupa epoca anului!). Pentru matinali ce poate fi mai frumos decat rosul pal al rasaritului, pe care Robert Cramer (consilier de stat ecologist, pentru cei care nu o stiu) il descrie chiar ca pe un "cadou etern". Este adevarat ca nu remarcam lumina natural adecat in anumite perioade cum ar fi in preajma unei faze de extrema sensibilitate personala sau, pentru unii, dupa zece zile de nori grosi. Revenit de doua saptamani de la Palexpo, stiu despre ce vorbesc devreme ce lumina zilei nu mi-a lipsit niciodata atat de mult, fiind privat de ea in halele immense, cu toate astea bine (poate prea mult.) luminate. Insa, spre deosebire de cea naturala, aceasta lumina, produsa de neoane, de lampi cu halogen si de fascicule colorate, nu aducea nici o caldura si aproape orbea, asemeni luminozitatii unei discoteci. De altfel virtutile fizice si psihice ale unei bai bune de soare nu mai au nevoie sa fie demonstrate.

Variatiile de lumina fac parte integrate din viata noastra, caci nu am putea trai intr-o lume luminata constant si uniform, aceasta fiind impotriva propriului nostru ceas biologic. Oricine a lucrat macar o data in tura de noapte sau a calatorit in tarile scandinave in perioada estivala, isi da foarte repede seama ca este greu, sau cel putin foarte obositor, sa adormi atunci cand sorele straluceste inaca afara. Cu toate astea ar fi gresit sa afirmam ca lumina naturala este perceptibila numai ziua. De fapt, luna plina poate aduce o cantitate de lumina considerabila, la fel ca o noapte cu multe stele, deci constituie si ele o forma de lumina naturala.

Luminozitatea naturala in oras depinde in mare masura de planul de amenajare urbana a acestuia. Stradutele inguste e care le putem intalni in orasul vechi, beneficiaza de o insorire mai restransa decat marile bulevarde. Orice ar fi, putem afirma ca luminozitatea unei strazi sau a unei piete joaca un rol ce nu este de neglijat in atractia sa populara.