| CATEGORII DOCUMENTE |
| Gradinita |
PROIECT DE ACTIVITATE DIDACTICA/ LECTIE
I. DATE DE IDENTIFICARE:
DATA: 20 noiembrie 2008
SCOALA: Colegiul National "Alexandru Papiu Ilarian", Tirgu-Mures
PROFESOR DE MATEMATICA:
PROFESOR METODIST:
PROPUNATOR:
CLASA: a XI-a A
ARIA CURRICULARA: Stiinte
OBIECTUL: Matematica
SUBIECTUL LECTIEI: Exercitii cu determinanti
TIPUL LECTIEI: Aprofundare
OBIECTIVE CURRICULARE:
v FUNDAMENTALE:
sa identifice date si relatii matematice si sa le coreleze in functie de contextul in care sunt definite
sa prelucreze date de tip cantitativ, calitativ, structural, contextual cuprinse in enunturi matematice
sa exprime caracteristicile matematice, cantitative sau calitative ale unei situatii concrere si a algoritmilor de prelucrare ale acestora
sa analizeze si sa interpreteze caracteristicile matematice a unei situatii-problema
sa utilizeze algoritmii si conceptele matematice pentru caracterizarea locala sau globala a unei situatii concrete
v OPERATIONALE(COMPETENTE SPECIFICE):
sa aplice corect proprietatile determinantilor in exercitii variate
sa determine valoarea unui determinant de ordinul 3 si 4.
sa decida care dintre proprietatile determinantilor (regulile de calcul) se poate aplica la calcularea unui determinant dat
sa rezolve corect o ecuatie cu determinanti.
METODE SI PROCEDEE DIDACTICE: exercitiul, explicatia, conversatia
MIJLOACE DE INVATAMANT: manualul, tabla
STRATEGIA DIDACTICA: explicativ-exersativa
EVALUARE: pe baza exercitiilor
NIVELUL DE PREGATIRE AL GRUPULUI TINTA: bun
CONTINUTUL INFORMATIV:
Proprietatile determinantilor
Care sunt proprietatile determinantilor pe care le-am studiat ora trecuta?
P1. ![]()
P2. Daca intr-un determinant elementele unei linii (sau coloane) sunt nule, atunci valoarea determinantului este zero.
P3. Daca intr-un determinant schimbam 2 linii (sau coloane) intre ele, obtinem un determinant egal cu opusul determinantului initial.
P4. Daca intr-un determinant 2 linii (sau coloane) sunt egale intre ele, atunci determinantul este nul.
P5. Daca intr-un
determinant inmultim toate liniile (sau coloanele) cu o constanta ![]() , atunci se obtine un determinant egal cu
, atunci se obtine un determinant egal cu ![]() inmultit cu
determinantul initial.
inmultit cu
determinantul initial.
P6. Daca intr-un determinant 2 linii (sau coloane) sunt proportionale, atunci deteterminantul este nul.
P7. Daca avem un
determinant de forma  atunci il putem scrie
ca suma a 2 determinanti astfel:
atunci il putem scrie
ca suma a 2 determinanti astfel: 

P8. Daca intr-un determinant o linie (sau coloana) este combinatie liniara de celelalte linii (sau coloane) atunci valoarea determinantului este egala cu 0.
P9. Daca intr-un determinant adaugam la o linie (sau coloana) elementele unei alte linii (sau coloane) inmultite cu o constata reala nenula, atunci valoarea determinantului ramane aceeasi.
P10. ![]()
P11. ![]()
P12. Determinatul matricii triunghiulare este egal cu produsul elementelor de pe diagonala principala.
P13. ![]()
Exercitii



 =
=


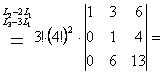
=![]()
![]()
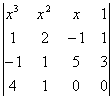 =0.
=0.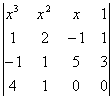

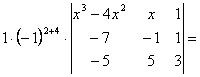

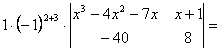
=![]()
![]()
![]()
![]()
Aceasta ecuatie se rezolva utilizand schema lui Horner.
Cautam solutiile printre divizorii intregi ai numarului 5.
![]()
|
|
|
|
|
|
Solutia este: x=1.
 =0.
=0. =
=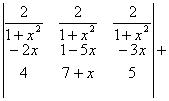
 =
=
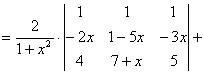
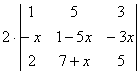
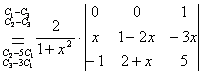 +
+
 =
=![]() =
=![]() =
=
=![]()

![]()
![]()
![]()
![]() , pentru
, pentru ![]()
![]()
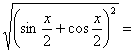
![]() =
=![]() , pentru
, pentru ![]()
![]()
![]()
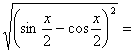
![]()
=![]() , pentru
, pentru ![]()

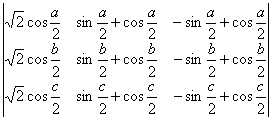

![]() .
.
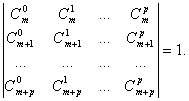
![]()
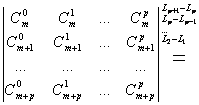



Folosim formula
de la combinari: ![]() , pe care o scriem sub urmatoarea forma:
, pe care o scriem sub urmatoarea forma: ![]() .
.
![]()
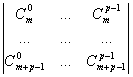
Acest determinant are aceeasi forma cu cel initial daca il inlocuim pe p cu p-1.
Cum ar arata urmatorul determinant, dupa ce efectuam aceleasi calcule?
![]()
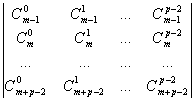
Aplicand succesiv acelasi algoritm obtinem:
![]()

BIBLIOGRAFIE:
Ganga M., Manual de matematica pentru clasa aXI -a, profil M1, M2, Editura Mathpress, 2003.
Nastasescu C., Nita C., Brandiburu M., Joita D., Culegere de probleme de algebra pentru liceu claseleIX-XII, Editura Rotech Pro, 1999.
Jinga I., Istrate Elena, Manual de pedagogie editia a II-a, Editura ALL, 2006.
II. DESFASURAREA PROPRIU-ZISA A ACTIVITATII/ LECTIEI
|
Etapele lectiei/ Timp |
Activitatea profesorului |
Activitatea elevilor |
Observatii |
|||||||||||||||||||||||||
|
1.Moment organizatoric/ 1min 2.Reactualizarea cunostintelor si Prezentarea suportului teoretic / 15min 3.Verificarea temei/ 10min 4.Anuntarea subiectului lectiei/ 1min 5.Exersarea propriu-zisa si Evaluarea rezultatelor obtinute / 20min 9.Incheierea activitatii/ 2min |
Solicit pregatirea caietului de teme si de clasa.Strig catalogul, trec absentii. Ii intreb: "Ce am avut de pregatit pentru astazi?" "Care sunt proprietatile determinantilor pe care le-am studiat ora trecuta?" Numesc cate un elev sa enunte cate o proprietate. "Ce tema ati avut pentru azi?" "Care exercitii nu le-ati rezolvat?" Rezolvam la tabla exercitiile dificile pe care nu le-au rezolvat acasa. La exercitiile mai putin dificile le dau indicatii cum sa le rezolve pentru data viitoare. "Astazi vom rezolva niste exercitii cu determinanti folosind proprietatile invatate." Scriu titlul pe tabla. Exercitii Le dictez enuntul exercitiului; elevul care urmeaza sa iasa la tabla va scrie exercisiul pe tabla.
Le pun intrebari ajutatoare si le dau indicatii pentru a rezolva determinantul. 2. Sa se rezolve ecuatia: 3. Sa se arate ca: =0. Se considera
Sa se arate ca oricare ar fi tripletul
"Pentru a calcula mai usor determinantul, sa incercam sa aducem functiile f, g si h la o forma mai simpla." "Vom folosi formulele de la trigonomerie pentru unghiuri duble." "Atunci determinantul va fi :" "Observam ca avem 2 coloane proportionale. Atunci determinantul va fi nul." Le spun ca s-au descurcat bine, le dau indicatii asupra caror formule si exercitii trebuie sa mai insiste. Le dau tema de casa: de invatat, de rezolvat |
Isi scot caietul de teme. Elevul de serviciu imi spune absentii(daca sunt). "Pentru astazi am avut de pregatit proprietatile determinantilor." "Proprietatile determinantilor pe care le-am studiat ora trecuta sunt: P1. P2. Daca intr-un determinant elementele unei linii (sau coloane) sunt nule, atunci valoarea determinantului este zero. P3. Daca intr-un determinant schimbam 2 linii (sau coloane) intre ele, obtinem un determinant egal cu opusul determinantului initial. P4. Daca intr-un determinant 2 linii (sau coloane) sunt egale intre ele, atunci determinantul este nul. P5. Daca intr-un determinant inmultim toate liniile (sau coloanele) cu o constanta , atunci se obtine un determinant egal cu inmultit cu determinantul initial. P6. Daca intr-un determinant 2 linii (sau coloane) sunt proportionale, atunci deteterminantul este nul. P7. Daca avem un determinant de forma atunci il putem scrie ca suma a 2 determinanti astfel: P8. Daca intr-un determinant o linie (sau coloana) este combinatie liniara de celelalte linii (sau coloane) atunci valoarea determinantului este egala cu 0. P9. Daca intr-un determinant adaugam la o linie (sau coloana) elementele unei alte linii (sau coloane) inmultite cu o constata reala nenula, atunci valoarea determinantului ramane aceeasi. P10. P11. P12. Determinatul matricii triunghiulare este egal cu produsul elementelor de pe diagonala principala. P13. "Pagina , exercitiile: " "Exercitiile: " Scriu in caiete exercitiile pe care nu le-au rezolvat acasa si sunt atenti la explicatiile de la exercitiile mai putin dificile. Exercitii
=
= Aceasta ecuatie se rezolva utilizand schema lui Horner. Cautam solutiile printre divizorii intregi ai numarului 5. Solutia este: x=1.
=
Isi noteaza tema in caiete si sunt atenti la explicatii. |
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5849
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved