SUBIECTELE DATE LA FAZA LOCALA A OLIMPIADEI DE MATEMATICA VASLUI - FEBRUARIE 2006

SUBIECTELE DATE LA FAZA LOCALA A OLIMPIADEI DE MATEMATICA VASLUI - FEBRUARIE 2006

CLASA A V A

1. Aflati restul impartirii numarului A= 2003²⁰⁰⁴ + 2004²⁰⁰⁵ + 2005²⁰⁰⁶ la 10.

2. Determinati cifrele a si b, stiind ca media aritmetica a numerelor

este 1375.

3. Determinati multimile A, B, C stiind ca :

a) , b) , c) ,

d) Multimile A, B, C au acelasi cardinal.

4. Intr-un garaj sunt 100 de masini cu 3 si 4 usi, dintre care 60 au culoarea rosie.

Un sfert din masinile rosii au patru usi iar jumatate din masinile care nu sunt rosii

nu au patru usi. Cate masini cu 4 usi sunt?

CLASA A VI A

1. Determinati numerele naturale a, b, c astfel incat sa aiba loc relatia:

.

2. Trei vanzatori au caiete cu acelasi pret. Primul a marit pretul cu 20% si apoi l-a

micsorat cu acelasi procent, al doilea a micsorat mai intai pretul cu 20% si abia

apoi l-a marit cu acelasi procent iar al treilea a lasat pretul neschimbat.

De la care vanzator ai cumpara acum si de ce?

3. Fie triunghiul isoscel ABC cu (AB) º (AC) si punctele D, E IBC, astfel incat BI(DC), CI(BE) si (BD) º(CE). Perpendiculara in D pe AD intersecteaza perpendiculara in E pe AE in punctul F. Sa se arate ca (AF este bisectoarea unghiului

4. Demonstrati ca un numar cu n cifre identice, n>1, nu poate fi patrat perfect.

CLASA AVII A

Fie numerele rationale nenule a, b si c astfel incat a + b, b + c si c sa fie

direct proportionale cu 10, 3 si .

a) aflati a, b si c daca a + 2b = 3c + 1;

b) aflati a, b si c astfel incat a b c sa fie natural si cat mai mic posibil.

2. a) Aflati toate numerele naturale n de doua cifre cu proprietatea ca I N

b)      Aflati restul impartirii numarului 7 3²⁰⁰⁶ la 5

3. Fie un triunghi oarecare ABC si M I (BC), N I (AC), P I (AB) a.i.

MN AB, PM AC si PN BC.

Demonstrati ca M, N si P sunt mijloacele laturilor triunghiului ABC.

4. Fie triunghiul ABC, D I (BC), (DE bisectoarea unghiului ÐADC, E I (AC),

(DF bisectoarea unghiului ÐADB, F I (AB), BE FD =

CF DE = si AD EF =

a)      demonstrati ca FE ll BC Û D mijlocul lui BC

b)      demonstrati ca MN ll FE Û P mijlocul lui EF

CLASA A VIII A

1 Aflati numerele naturale nenule a, b, c astfel ca

.

2. Sa se rezolve in R ecuatia urmatoare:

3. Daca a,b I ( 0,1] si n > 0, demonstrati ca:

.

4. Se considera un cub de latura 1 si in interiorul sau o multime finita de puncte M

cu proprietatile;

a) M are cel putin trei puncte;

b) Distanta dintre orice doua puncte din M este cel mult egala cu d, 0 < d < 1.

Pentru fiecare punct PIM se noteaza cu cea mai mica distanta de la P la

celelalte puncte din M-. Demonstrati ca:

CLASA A IX A

1. Sa se arate ca nu exista functii f: N N pentru care sa avem

(1) f (3n+1) £ f (3n+4) -1

(2) f (5n+1) ³ f (5n+7) -1

pentru orice n natural.

2.Sa se demonstreze inegalitatea:

.

3. Fie triunghiul ABC. In planul sau consideram punctele D si M astfel ca

si .

a) Aratati ca punctele C, M, D sunt coliniare;

b) Daca AM BC= aflati valoarea raportului .

4. Sa se arate ca, pentru orice m,nIN^*, avem:

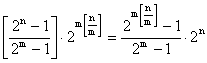
CLASA A X A

1. Sa se compare numerele lg² (5+) si lg (6+

2. Rezolvati in R :

3. Se considera un triunghi ascutitunghic ABC. Stiind ca lungimile laturilor sale a,

b, c sunt in progresie aritmetica, demonstrati ca are loc inegalitatea:

asinC+bsinB+csinA ≤ p

4. Fie numere complexe distincte avand acelasi modul r. Aratati ca:

CLASA A XI A

Fie X, YI M_n (C) si a,b IC^* astfel incat XY=aX+bY. Aratati ca

XY=YX.

Gasiti valoarea minima a unui determinant de ordinul al treilea avand elementele egale cu pe diagonala principala si pe fiecare linie si coloana suma elementelor 1.

3. Fie progresia aritmetica a₁, a₂ , .,a_n , . cu ratia si primul termen strict

pozitive. Sa se calculeze:

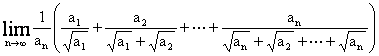
4. Fie kIN^* si un sir (a_n)_n³ astfel incat [a_n+1] = [a_n]^k + (k+1)[a_n] + 1, oricare ar fi

nIN^*. Demonstrati ca daca (a_n)_n³ este convergent atunci k=2.

CLASA A XII A

. Fie (G, ) un monoid, cu proprietatile:

a) ÌG; b) 2 2 = 6; c) 4 4 = 1, unde 1 este elementul

neutru; d) 2 este element simetrizabil.

Rezulta ca 3 este simetrizabil?

2. Determinati o functie f:R R, f(0) = 0, stiind ca admite o primitiva F astfel

incat F(x) + f(x) = sinx, oricare ar fi xIR

3. Calculati 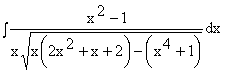, x II.

4. Fie (G, ) un grup finit cu p elemente (pIN, prim). Sa se demonstreze ca

daca f :G G este un morfism astfel incat exista xIG-, cu f(x)=x, atunci f=1_G