| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
ANALIZA TERMODINAMICA A GAZELOR IDEALE
SI A AMESTECURILOR DE GAZE
Definitie
Gazul perfect sau ideal reprezinta un gaz ipotetic (un model conceptual), caracterizat de urmatoarele ipoteze:
- gazul este rarefiat, distanta medie mijlocie dintre molecule este mare, astfel incat fortele intermoleculare sunt neglijabile; asupra unei molecule nu actioneaza forte apreciabile decat in timpul unei ciocniri;
- numarul total de molecule este foarte mare;
- volumul real ocupat de molecule este neglijabil in comparatie cu volumul recipientului;
- miscarea moleculelor se supune mecanicii newtoniene; miscarea moleculelor este rectilinie si uniforma, iar energia interna a gazului se reduce la energia cinetica a moleculelor sale;
- miscarea este complet haotica (directiile de miscare a moleculelor sunt considerate ca fiind egal de probabile);
- procesul de ciocnire a moleculelor este similar ciocnirii unor sfere perfect elastice.
Ecuatia de stare a gazelor perfecte
Legea BOYLE-MARIOTTE
R. Boyle si, independent, E.
Mariotte au aratat ca pentru transformarile izoterme
produsul dintre presiunea gazului si volumul ocupat de gaz este constant:
p1v (p1,t)
= p2v (p2,t)
p1v1 = p2v2
ecuatie care se poate scrie sub forma generala:
pv = const.
de unde:
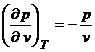
ceea ce arata ca valoarea coeficientului de compresibilitate izoterma:
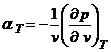 este in acest caz:
este in acest caz: ![]()
Legea Gay-Lussac
G. Gay-Lussac a obfinut pentru transformarile izobare, ca volumul un mase de gaz variaza cu temperatura, conform relatiei:
![]()
![]() unde:
V0 este volumul gazului ideal la 0C;
unde:
V0 este volumul gazului ideal la 0C;
b0 este coeficientul de dilatare volumica izobara, avand, la presiuni suficient de scazute, aceeasi valoare pentru toate gazele:
![]() la temperatura de 0C.
la temperatura de 0C.
Ecuatia conduce la: V=V0b0 T
In acest caz se observa ca valoarea coeficientului de dilatare volumica izobara
este: ![]()
Legea lui CHARLES
Pentru transformarile izocore: p = p0 (1+;v,0 t)
unde b este coeficientul de compresibilitate izocora.
Ecuatia conduce la: p = p0 ;v0 T
In acest caz se observa ca
valoarea coeficientului de compresibilitate izocora devine: 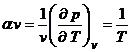
Pentru gazul ideal bare aceeasi valoare cu ;v.
Deducerea ecuatiei de stare a gazelor perfecte
Introducand expresiile
coeficientilor termodinamici in expresia diferentialei
presiunii: 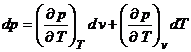
obtinem: ![]() , de unde, prin integrare, obtinem ecuatia:
, de unde, prin integrare, obtinem ecuatia:
pV = RT
unde R este o constanta particulara a gazului respectiv [j/(kg K).
Aceasta poarta numele de ecuatia termica de stare a gazului perfect.
pV = p0Vt - p0V0 b0T = mp0v0 b0T = const., de unde:
pv = p0v0 b0T
Termenul p0v0 b0T, notat cu R, reprezinta lucrul mecanic efectuat de unitatea de masa a gazului respectiv, la presiunea p0, daca temperatura gazului creste cu un grad.
Ecuatia energiei interne
Din ecuatia fundamentala a Termodinamicii scrisa sub forma:
d U=T d S - p d V
rezulta expresia:
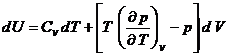
de unde, prin identificare cu: 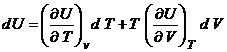
se obtine relatia: 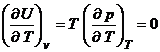
cunoscuta sub numele de ecuatia energiei interne.
Pentru un gaz perfect rezulta:
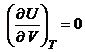
Relatie cunoscuta sub numele de legea lui Joule.
Ecuatia energiei interne conduce la concluzia ca, pentru un gaz ideal, energia interna depinde doar de temperatura:
U = U (T)
Entalpia unui gaz perfect rezulta:
H = U + PV = U + RT
deci entalpia unui gaz perfect depinde doar de temperatura:
H = H (T)
Caldurile specifice ale gazului perfect
Caldura specifica la volum constant
Din ecuatia: 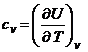 obtinem,
pentru un gaz ideal, pentru care u = u (T):
.
obtinem,
pentru un gaz ideal, pentru care u = u (T):
.
![]() ,
de unde d u = cv d T, d T = mcv d T
,
de unde d u = cv d T, d T = mcv d T
Caldura specifica la presiune constanta
Din ecuatia: 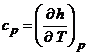 obtinem,
pentru un gaz ideal, pentru care h = h (T):
obtinem,
pentru un gaz ideal, pentru care h = h (T):
![]() de unde d h = cv d T,
d H = m cv d T
de unde d h = cv d T,
d H = m cv d T
Rezulta: ![]()
De unde obtinem relatia lui Robert Mayer pentru gaze perfecte:
cp-cv=R
Elemente de teoria cinetico-moleculara a gazelor perfecte
Sarcina
fundamentala a teoriei este aflarea semnificatiei moleculare a
marimilor de stare si deducerea legilor si ecuatilor de stare, in functie de
proprietatile si de starea de miscare a moleculelor.
Proprietatile sistemelor macroscopice, formate dintr-un numar foarte mare particule, nu sunt direct deductibile din caracteristicile particulelor constituente (legatura dintre proprietatile sistemului si cele ale particulelor nu este evidenta). Mai mult, notiunile de temperatura, presiune, viscozitate, conductivitate termica nu au sens pentru o singura particula.
Semnificafia cinetico-moleculara a marimilor de stare
Presiunea. Presiunea exercitata de un gaz asupra peretilor recipientului care se afla gazul reprezinta efectul mediu al ciocnirilor moleculelor cu peretii recipientului (presiunea reprezinta impulsul transportat de molecule in unitatea timp pe unitatea de suprafata a peretelui recipientului).
In ipoteza ca toate moleculele gazului se misca toate cu aceeasi viteza se demonstreaza relatia dintre presiunea unui gaz ideal si viteza de translatie a moleculelor lui:
![]() ,
unde
,
unde ![]() ,reprezinta
concentratia moleculelor (numarul de molecule pe unitatea de volum), iar m
reprezinta masa unei molecule. Relatia se poate scrie sub forma:
,reprezinta
concentratia moleculelor (numarul de molecule pe unitatea de volum), iar m
reprezinta masa unei molecule. Relatia se poate scrie sub forma: 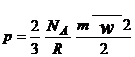
Unde NA este numarul lui Avogadro.
Termenul
k = ![]() ,
reprezinta constanta lui Boltamann, aratand legatura dintre energia medie de
translatie a unei molecule si temperatura absoluta
,
reprezinta constanta lui Boltamann, aratand legatura dintre energia medie de
translatie a unei molecule si temperatura absoluta ![]()
Energia cinetica a gazului este: 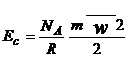
Astfel, temperatura poate fi considerata ca o masura a starii energetice (masoara energia cinetica medie a moleculelor gazului respectiv).
Temperatura, ca parametru statistic, reprezinta o masura a intensitatii miscarii termice.
Relatiile precedente raman valabile si in cadrul unei distributii neuniforme a moleculelor ( cazul real), daca introducem notiunea de viteza patratica medie.
Astfel, energia cinetica a
tuturor moleculelor este ![]() ,
unde ni, reprezinta numarul de molecule
care se misca cu viteza wi, astfel incat energia cinetica medie a unei molecule
este:
,
unde ni, reprezinta numarul de molecule
care se misca cu viteza wi, astfel incat energia cinetica medie a unei molecule
este:
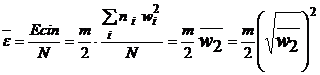
Putem sa calculam astfel energia
cinetica totala folosind o formula simpla, si cand moleculele s-ar misca toate
cu aceeasi viteza ![]() (viteza patratica medie).
(viteza patratica medie).
Distributia Maxwell-Boltzmann
Legea statistica de distributte Boltzmann pentru un sistem ale carui particule interactioneaza slab si care se gaseste in prezenta unui camp conservativ de forte se exprima prin relatia:
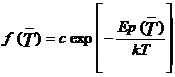 ,unde
Ep reprezinta energia potentiala a moleculei in camp, iar constanta C se
determina din conditia de normare:
,unde
Ep reprezinta energia potentiala a moleculei in camp, iar constanta C se
determina din conditia de normare:
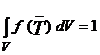
Legea statistica de distributie Maxwell dupa componentele vitezelor considera independenta statistica a miscarii moleculelor pe directii diferite. Astfel considerand dn numarul moleculelor din unitatea de volum la care proiectiile vitezei sunt cuprinse intre wx si wx+d wx, wy si wy+d wy, wz si wz +d wz,probabilitatea ca o molecula sa aiba proiectiile vitezei intre aceste limite este dn/n si se poate calcula dupa teorema probabilitatilor compuse, considerand evenimentele componente sunt independente intre ele:
dn/n = f ( wx )- f( wy )- f ( wz) d wx d wy d wz
Prin integrare si impunerea conditiei de normare se obtin relatiile:
![]()
de unde: 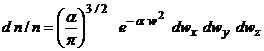
In spatiul vitezelor volumul
sferei de raza w este![]() ,
de unde
,
de unde
d Vw= 4 w2 dw. In acest spatiu dwx, dwy, dwz = d Vw, astfel incat obtinem
d n/n = f (w)dw.unde functia de distributie dupa modulul vitezelor este:
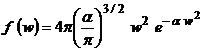
Concentratiile ![]() satisfac legea de distributie Boltzmann si constanta
;
satisfac legea de distributie Boltzmann si constanta
;
rezulta:
![]()
Se definesc urmatoarele viteze caracteristice:
- viteza cea mai probabila, pentru care functia de distributie ia valoarea maxima:
![]()
Se observa ca putem scrie functia de distributie sub forma:
- viteza medie, care reprezinta media modulului
vectorului viteza (valoarea medie a ![]() este nula):
este nula):
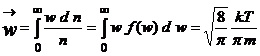
- viteza patratica medie, care reprezinta media patratelor vitezelor:
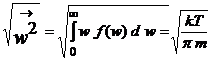
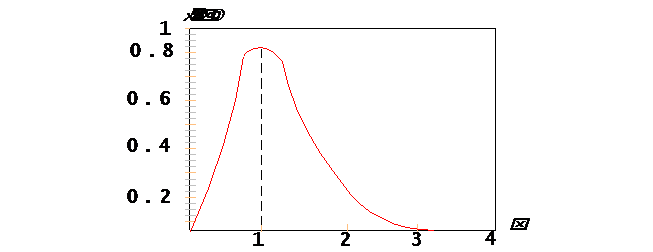
Functia de distributie Maxwell-Boltzmann
In cazul unei distributii izotrope (nici o directie nu este privilegiata),
Rezulta: 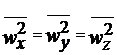
Avem insa , ![]() , de
unde:
, de
unde:
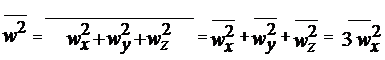
Deoarece 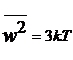 ,
obtinem:
,
obtinem: 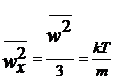
Una din principalele legi considerate in cadrul teoriei cinetico-moleculare clasice este legea echipartitiei energiei, conform careia energia unei particule in miscare termica se distribuie in mod egal pe diversele grade de libertate de miscare a moleculelor, fiecarui grad de libertate corespunzandu-i aceeasi valoare a energiei cinetice medii moleculare:
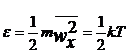
Energia interna a unui kmol de gaz ideal este:
U = NA*i*e=![]() ,iar
energia interna a unui kg de gaz ideal este:
,iar
energia interna a unui kg de gaz ideal este:
![]()
unde i reprezinta numarul de grade de libertate de miscare a moleculelor.
i = 3 pentru moleculele monoatomice (numai miscare de translatie);
i = 5 pentru moleculele biatomice (2 grade de libertate in miscarea rotatie);
i = 6 pentru moleculele tri si poliatomice (3 grade de libertate in miscarea de rotatie).
Tinand cont ca pentru gazul ideal, conform ecuatiei calorice de stare, avem:
d u = cv d T ,
obtinem: ![]()
Cu relatia lui Robert Mayer
objinem expresia caldurii specifice la presiune constanta: ![]()
si apoi expresia exponentului adiabatic:
![]()
Legea lui Avogadro
Aplicand relatia generala a
presiunii pentru doua volume egale de gaze cu masele moleculelor m1 si m2 si
vitezele patratice medii ![]() si
si ![]() aflate la aceeasi presiune, se obtine:
aflate la aceeasi presiune, se obtine:
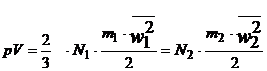
Gazele finnd la aceeasi temperatura, energiile cinetice medii sunt egale si se obtine N1 = N2, adica "volume egale de gaze, in conditii identice de temperature si presiune, contin acelasi numar de molecule"
Pentru exprimarea cantitativa a legii lui Avogadro, este necesara precizarea unor notiuni privind unitatile de masura corespunzand cantitatii de substanta.
Astfel, masa unui atom, exprimata in kilograme, se numeste masa atomica absoluta.
De asemenea, masa unei molecule, exprimata in kilograme, se numeste masa moleculara absoluta.
Deoarece valorile masei atomice
absolute sunt extrem de mici, se prefera folosirea unitatii atomice de masa (a.m.u.),
egala cu a douasprezecea parte din masa atomului izotopului de carbon ![]()
![]()
1 a.m.u. = 1.667x 10-27 kg.
Masa unui atom exprimata in unitati
atomice de masa este o marime
adimensionala numita masa atomica relativa, iar masa unei molecule exprimata in
unitati atomice de masa este o marime adimensionala numita masa moleculara
relativa.
Unitatea cantitatii de substanta
este molul, care contine tot atatea entitati elementare cate sunt in 12 g de
carbon ![]() .
Molul reprezinta asadar masa de substanta
exprimata in grame prin acelasi numar ca si masa atomica relativa. Masa unui
mol de substanta, exprimata in grame, se numeste masa molara. In tehnica se
prefera exprimarea masei molare drept masa, exprimata in kg, a unui kmol de
substanta.
.
Molul reprezinta asadar masa de substanta
exprimata in grame prin acelasi numar ca si masa atomica relativa. Masa unui
mol de substanta, exprimata in grame, se numeste masa molara. In tehnica se
prefera exprimarea masei molare drept masa, exprimata in kg, a unui kmol de
substanta.
Numarul de molecule care se gasesc intr-un kilomol de substanta poarta numele de numarul lui AVOGADRO:
NA = 6.023 x 1023 molecule/mol = 6.023 x 1026 molecule/kmol
Legea lui Avogadro conduce la conduzia ca volumul molar are aceeasi valoare pentru toate gazele, in aceleasi conditii de temperatura si presiune. In particular, la starea normala, caracterizata de:
PN = 101325 N/m2 = 760 mm. Hg, TN = 273.15 K
volumul molar are valoarea: V N = 22.414 m3/kmol.
Pe baza legii lui Avogadro, ecuatia termica de stare a gazului perfect poate primi o forma generala, indiferent de natura gazului. Astfel, considerand o cantitate de substanta de 1 kilomol, avem:
pV = m R T = M n R
T, unde M =![]() ,
reprezinta masa molara a gazului respectiv.
,
reprezinta masa molara a gazului respectiv.
Rezulta ecuatia:
pV = n R T, unde
unde: R = RM [J/(kmol K]
reprezinta constanta universala a gazelor perfecte. Pentru condittile normale se obtine:
![]()
Constanta unui gaz se determine
cu relatia: 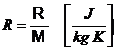

Transformarile fundamentale ale gazelor perfecte
Studiul transformarilor fundamentale ale gazelor perfecte este facut in ipoteza ca transformarile sunt reversibile.
Pentru fiecare transformare urmarim:
- determinarea parametrilor finali in functie de cei initiali;
- variafia marimilor de stare si a marimilor de proces;
- reprezentarea in diagrama p-v si in diagrama T-s.
Transformarile fundamentale sunt:
- transformarea izocora;
- transformarea izotermica;
- transformarea izobara;
- transformarea adiabatica;
- transformarea politropica.
Transformarea izocora
Reprezinta transformarea in decursul careia volumul ramane constant:
V = const, sau v = const.
Transformarea izocora a unui gaz perfect este caracterizata de legea lui Charles :
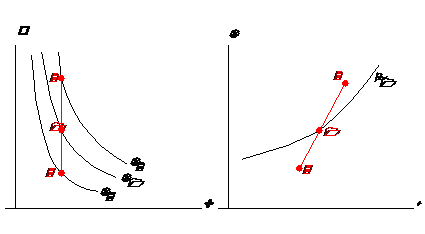
3
Transformarea izocora In diagramele p - v si T - s
1-2: proces de incalzire, 1 -3: proces de racire
Caldura schimbata cu mediul exterior este:
Q12 = m cv (T2 - T1)
Lucrul mecanic total este: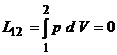
Variatia energiei interne, variatia entalpiei si variatia entropiei sunt date de relatiile:
D U= m cv (T2 - T1)
D H= m cp (T2 - T1)
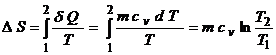
Transformarea izobara
Reprezinta transformarea in decursul careia presiunea ramane constanta: p = const.
Transformarea izobara a unui gaz perfect este caracterizata de legea lui Gay - Lussac:
![]()
Caldura schimbata cu mediul exterior este: Q12 = m cp (T2 - T1)
Lucrul mechanic total este: 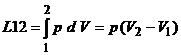 ,
Observand ca, pentru transformarea izobara, lucrul mecanic specific este: l =
p(v2 - v1) = R(T2-T1), putem gasi interpretarea fizica:
,
Observand ca, pentru transformarea izobara, lucrul mecanic specific este: l =
p(v2 - v1) = R(T2-T1), putem gasi interpretarea fizica:
"Constanta gazului reprezinta lucru; mechanic specific efectuat intr-o transformare izobara, pentru a obtine o variatie unitara a temperaturii."
Variatia energiei interne si variatia entapiei sunt date de relatiile:
D U= m cv (T2 - T1) , D H= m cp (T2 - T1)
Variatia entropiei este data de relatia
![]()
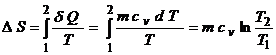
Transformarea izotermica
Reprezinta transformarea in decursul careia temperature ramane constanta:
T = const. Transformarea izoterma a unui gaz perfect este caracterizata de legea Boyle-Mariotte: pv = const, p1 v1 = p2 v2
Ca urmare, viriatia energiei interne si variatia entalpiei sunt nule. D U= 0 , D H= 0
Cu relatia primului principiu al Termodinamicii pentru sisteme inchise, obtinem ca lucrul mechanic si caldura schimbate cu exteriorul intr-o transformare izotermica sunt egale:
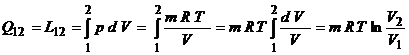
Variatia entropiei este data de
relatia: 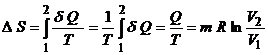
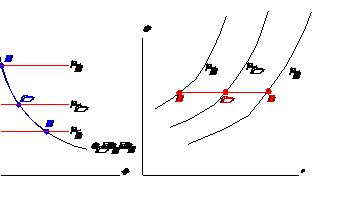
Transformarea izotermica in diagramele p - v si T-s
1-2: proces de destindere, 1 - 3: proces de comprimare
Transformarea adiabatica
O transformare adiabatica este caracterizata de lipsa transferului termic intre sistemul termodinamic si mediul exterior dq = 0. Rezulta astfel: Q12=0
Conform primului principiu al Termodinamicii pentru sisteme inchise, se obtine:
-L12=U2-U1, sau, sub forma diferentiala: du + pdv = 0
In cazul gazelor perfecte, avem: pv = RT,
cp - cv = R,
du = cv d T,
![]()
cv(p d p + v d p) + (cp - cv) p d v = 0
sau cv v d p +
cv p d v = 0, de unde : ![]()
Cu notatia:![]() care
reprezinta expresia exponentului
adiabatic pentru gaze perfecte, se obtine:
care
reprezinta expresia exponentului
adiabatic pentru gaze perfecte, se obtine:
![]()
Din expresia se deduce coeficientul unghiular al adiabatei in diagrama p - v
![]()
Pentru o transformare adiabatica , lucrul mecanic specific este:
![]()
Transformarea politropica
Conform Primului Principiu al Termodinamicii, avem:
dq = d u + p d v, dq = d h - v d p ;
Putem scrie, in general: dq = d u - v d p,
unde c reprezinta caldura specifica procesului respectiv:
- pentru un proces adiabatic c = 0 ;
- pentru un proces izobar c = cp ;
- pentru un proces izocor c = cv ;
- pentru un proces izoterm c = ∞ .
Pentru gazul ideal, avem relatiile: d u = cv d T ; d h = cp d T
Inlocuind:
c d T = cv d T+ p d v → (c - cv) d T = p d v
c d T = cp d T- v d p → (c - cp) d T =- v d p
unde: ![]() ,
notand cu n =
,
notand cu n = ![]() ,
avem : n * p d v = - v d p
,
avem : n * p d v = - v d p
Integrand obtinem relatia:
N ln v + ln p = ln c, adica p vn = const astfel incat n a fost denumit exponentul politropic.
Deoarece procesul considerat a fost ales arbitrar, inseamna ca relatia transformarii este general valabila, pentru orice transformare particulara:
- pentru transformarea izobara avem p = const., deci n = 0;
- pentru transformarea izotermica avem pv = const., deci n = 1;
- pentru transformarea adiabatica 8<7 =
- pentru transformarea izocora v = const. ; cum din ecuatia politropei avem
pentru a avea v = const, trebuie sa avem p1/n = const. => n = ∞. Pentru studiul concavitatii curbei in diagrama p - v, plecam de la ecuatia
![]() ,
,
Functia f(n) = n(n +1)
Pentru -∞ n < -l si 0 < n < ∞ avem n(n +1) > 0, iar pentru -1 < n < 0 avem n(n +1) < 0.
Pentru n = -1 se ob{ine ecuatia p = const, x v, deci graficul transformarii politropice in diagrama p - v este o linie dreapta care trece prin origine.
Pentru n = 0 se obtine ecuatia p = const, (transformarea este izobara).
Din relatia de definire a exponentului politropic rezulta expresia specifice caracteristice procesului politropic:
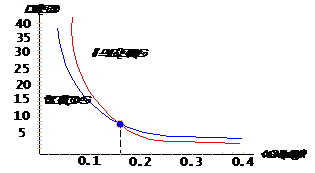
In figura se prezinta variatia caldurii specifice caracteristice procesului politropic in functie de exponentul politropic n.
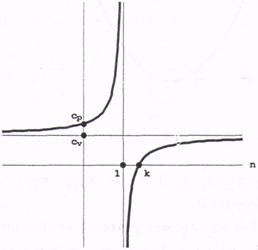
Se observa ca pentru 1 < n< k avem c < 0 , adica daca dq < 0 => dT > 0 (sistemul cedeaza caldura mediului si totusi se Tncalzeste!) si daca 8g > 0 => dT < 0 (sistemul primeste caldura si totusi se raceste!). Acest lucru se explica prin faptul ca, pentru o transformare in aceasta zona, avem:
![]() |
l12| > | q12|
|
l12| > | q12|
Lucrul mecanic pentru o transformare politropica reversibila este:
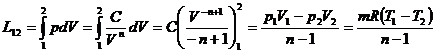
unde am tinut cont ca pentru o
transformare politropica pVn =C
Caldura schimbata intr-un proces politropic este:
![]()
- daca (rx - T2) > 0 , se obtine 112 >g12>0 si u2 - u: < 0 (in procesul politropic de destindere avand exponentul politropic 1 < n < k , pentru producerea lucrului mecanic este nevoie, pe langa aportul de caldura din exterior si de preluarea unei parti din energia interna, astfel incat gazul se raceste);
- daca (T1 - T2) < 0 , se obtine Z12 < ql2 < 0 si u2-ul>0 (in procesul de comprimare, caldura cedata este mai mica decat lucrul mecanic 'primit', diferen^a aflandu-se in cresterea energiei interne, deci temperatura gazului creste). ;
Procesele
politropice se pot reprezenta grafic cu multa usurinta intr-o
diagrama logaritmica, deoarece ecuatia pvn =C se poate scrie:
ln p = -n ln u + ln C
Procesul (de comprimare sau destindere) se desfasoara foarte lent, incat corpul are permanent aceeasi temperatura cu gazul. Caldura dQ schimbata < gaz intr-o transformare elementara contribuie In totalitate la variatjia energiei interne a corpului de contact, deoarece ansamblul gaz - corp este izolat adiabatic fata de exterior.
Variatia entropiei gazelor perfecte pentru o transformare oarecare
Fiind un parametru de stare, variatia entropiei nu depinde decat de starea finala si de cea initiala a unei transformari . In cazul unei transformari oarecare, reversibila sau ireversibila, variatia de entropie poate fi calculata folosind orice combinatie de procese reversibile de la starea initiala la cea finala.
Plecand de la ecuatia fundamentala a Termodinamicii, pentru procese reversibile:
![]()
rezulta:
![]()
Am obtinut astfel o relatie diferentiala pentru s = s(T,v).
Tinand cont de ecua|ia de stare a gazelor perfecte
pv = RT, obtinem, prin diferentiere:
d(pv) = RdT,
de unde, prin impartire cu pv:
dv/v + dp/p = dT /T
Pentru a obtine o relatie diferentiala pentru s = s(T,p), inlocuim termenul dv /v
si rezulta, tinand cont de relatia lui Robert Mayer pentru gaze perfecte cp = cv +R
![]()
de unde, prin integrare:
![]()
Diferitele expresii de mai sus conduc la calculul variatiei entropiei pentru diverse transformari reversibile particulare.
Astfel:
- pentru transformarea izotermica reversibila:
![]()
pentru transformarea izocora reversibila:
![]()
- pentru transformarea izobara reversibila:
![]()
pentru transformarea politropica reversibila:
![]()
In mod evident, pentru evident pentru transformarea adiabatica reversibila:
s2 - sl = 0 sau s2 = s1 , pentru care transformarea se mai numeste izentropica.
Variatia exergiei gazelor perfecte
Pentru un curent de substanta, exergia specifica (raportata la unitatea de masa) este:
ex = (h - h0) - T0 (s - s0),
indicele '0' se refera la parametrii mediului ambiant.
Intr-o transformare 1 - 2, exergia curentului de substanta va fi:
D(ex) = ex2 -ex1 = (h2 -h1) - T0(s2 -s1)
In cazul gazelor perfecte, avem:
h2-h1 = cp (T2 - T1),
astfel incat variatia exergiei gazelor perfecte se poate calcula cu relatia:
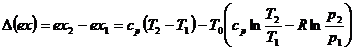
Amestecuri de gaze perfecte
Compozitia amestecurilor de gaze
Prin amestec de gaze intelegem o mai multe gaze care ocupa impreuna acelasi volum. In cele ce urmeaza consideram doar amestecurile de gaze in care nu au loc reactii chimice intre gaze.
Masa totala a unui amestec de gaze este data de suma maselor componente.De asemenea, numarul total de kilomoli este egal cu suma numerelor de kilomoli pentru fiecare gaz component.
Pentru caractcrizarea compozitiei unui amestec de gaze se introduc urmatoarele marimi:
- participatia (fractia) masica, definita prin relatia:
![]()
participafia (fractia) volumica, definita prin:
![]()
unde Vi reprezinta volumul partial ocupat de componentul 'i' (prin volum partial intelegem volumul ocupat de un component, separat din amestec, in aceleasi conditii de temperatura si presiune cu amestecul).
participafia (fracfia) molara, definita prin relatia:
![]()
Legile amestecurilor de gaze perfecte
Legea lui Dalton
Considerand ca unui amestec de gaze perfecte i se poate aplica ecuatia de stare a gazelor perfecte (deci amestecul de gaze perfecte poate fi considerat glc ca un gaz perfect), avem:
Pam Vam = n R Tam = mam Ram Tam
Scriind ecuatia de stare pentru fiecare component si impartind cele 2 relatii obtinem:
![]()
de unde, prin sumare rezulta
legea lui Dalton: ![]()
Legea lui Amagat
Scriind ecuatia de stare pentru fiecare component, cu considerarea volumelor partiale:
PamVi = ni R Tam = mi Ri Ta
putem exprima:
![]()
rezulta legea lui Amagat: 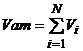
Se observa ca putem scrie, pentru gaze perfecte:
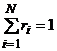
De asemenea, se remarca faptul ca, pentru gaze perfecte participatia volumica si cea molara coincid:
Energia interna, entalpia si caldurile specifice masice ale unui amestec de gaze perfecte
Fiind o marime extensiva, energia interna a amestecului de gaze ideale este egala cu suma energiilor interne ale gazelor din amestec:
![]()
ecuatie pe baza careia gasim, pentru gaze ideale, relatia caldurii peciftce la volum constant:
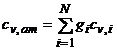
Entalpia amestecului este data de relatia:
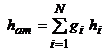
care conduce, pentru gaze ideale, la relatia caldurilor specifice la preiunes constanta:
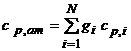
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3675
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved