| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
CINEMATICA SOLIDULUI RIGID
In capitolul anterior s-a aratat
ca a studia miscarea unui punct inseamna a determina la orice
moment t de timp , pozitia ![]() , viteza
, viteza ![]() si acceleratia
si acceleratia ![]() ale acestuia .
ale acestuia .
In cazul unui solid rigid , problema se pune analog , cu deosebirea ca este vorba de infinitatea p.m. care alcatuiesc solidul . la prima vedere , numarul necunoscutelor scalare pare foaret mare , dar ipoteza rigiditatii corpului reduce numarul necunoscutelor .
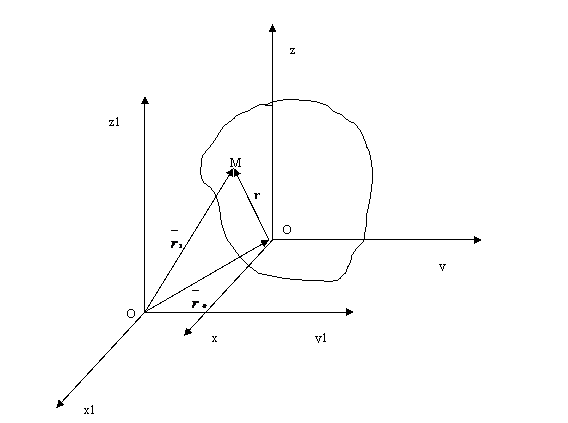
Presupunem un rigid (figura 1 ) a carui miscare este raportata la un sistem de referinta x1O1y1z1 . Daca se determina miscarea unui punct oarecare M al corpului , problema stadiului miscarii este rezolvata . Pozitia punctului M fata de sistemul de referinta fix este definit prin vectorul de pozitie .
![]() (1)
(1)
z
![]()
z1

![]()
 z
z
M
y
y
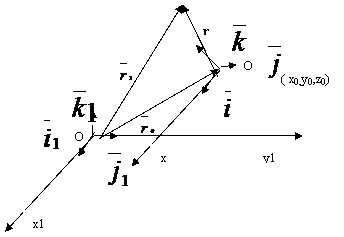
Pentru a preciza punctul M al rigidului trebuie sa definim pozitia lui fata de un sistem de referinta solidar legat de corp , de exemplu sistemul xOyz , avad originea intr-un punct O al corpului . Fata de acest sistem , punctul M nu-si schimba pozitia relativa , deci coordonatele lui x, y, z raman constante in timp .
Vectorul de pozitie este un vector cu modulul constant in timp si directie variabila .
![]() (2)
(2)
Pozitia triedrului
mobil fata de triedrul fix este definita prin vectorul ![]() al originii triedrului
mobil si prin versorii ai axelor
al originii triedrului
mobil si prin versorii ai axelor ![]() ;
; ![]() ;
; ![]() ai axelor Ox , Oy, Oz .
ai axelor Ox , Oy, Oz .
Intre cei trei vectori exista relatia :
![]() (3)
(3)
In aceasta relatie
apar ca functii derivabile in raport cu timpul ![]() (punctul O se
deplaseaza odata cu corpul ) si versorii
(punctul O se
deplaseaza odata cu corpul ) si versorii ![]() ,
, ![]() ,
, ![]() ai axelor sistemului
de referinta solidar legat de corp (care isi modifica
directiile odata cu miscarea solidului ) .
ai axelor sistemului
de referinta solidar legat de corp (care isi modifica
directiile odata cu miscarea solidului ) .
Observatie .
Un vector functie de timp se exprima cu ajutorul a trei functii
scalar de timp (proiectiile lui pe axe) . Astefel , se para ca
vectorul ![]() din relatiile anterioare se exprima cu ajutorul a 1
2 functii scalare de timp ( cate 3 pentru fiecare vector
din relatiile anterioare se exprima cu ajutorul a 1
2 functii scalare de timp ( cate 3 pentru fiecare vector ![]() ,
, ![]() ,
, ![]() ,
, ![]() ). Aceste functii nu sunt independente , deoarece se pot
scrie relatiile :
). Aceste functii nu sunt independente , deoarece se pot
scrie relatiile :
![]() (4)
(4)
![]() (5)
(5)
Rezulta ca
vectorul de pozitie ![]() se
exprima cu ajutorul a 6 funtii scalare de timp independent :trei
definesc pozitia originii O a sistemului de referinta mobil ,
iar celelalte 3 definiti ( prin versorii
se
exprima cu ajutorul a 6 funtii scalare de timp independent :trei
definesc pozitia originii O a sistemului de referinta mobil ,
iar celelalte 3 definiti ( prin versorii ![]() ,
, ![]() ,
, ![]() ) pozitiile axelor acestui sistem .
) pozitiile axelor acestui sistem .
Se obtine odata in plus numarul gradelor de libertate ale unui solid rigid liber .
DISTRIBUTIA VITEZELOR
Viteza punctului M in raport cu sistemul de referinta fix se obtine prin derivarea in raport cu timpul a relatiei :
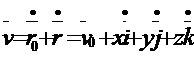 (6)
(6)
unde v 0 este viteza originii O a sistemului mobil .
Pentru a putea exprima vectorii ![]()
![]()
![]() prin proiectiile lor pe axele Ox , Oy
si Oz se tine seama de faptul
ca proiectia unui vector pe o axa este egala cu produsul
scalar dintre vectorul respectiv si versorul axei , deci :
prin proiectiile lor pe axele Ox , Oy
si Oz se tine seama de faptul
ca proiectia unui vector pe o axa este egala cu produsul
scalar dintre vectorul respectiv si versorul axei , deci :
![]()
![]() (6)
(6)
![]()
Se porneste de la produsul scalar
![]() pe care il derivez
si se obtine :
pe care il derivez
si se obtine : ![]() si tinand seama de comutativitatea produsului scalar ,
rezulta
si tinand seama de comutativitatea produsului scalar ,
rezulta
![]() (7)
(7)
Abalog se obtine si ![]() si
si ![]()
Consideram produsul scalar ![]() . Prin derivarea
acestei relatii se obtine :
. Prin derivarea
acestei relatii se obtine :
![]() (8)
(8)
Convenim sa notam aceasta valoare scalara cu ωz .
Similar obtinem :
![]() si
si
![]()
Rezulta :
![]()
![]() (9)
(9)
![]()
Relatiile obtinute anterior se pot rescrie astfel ( ca matrici ) :
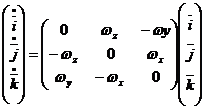 (10)
(10)
Inmultind relatia (10) cu vectorul ( x y z)
rezulta :
 (11)
(11)
![]() (12)
(12)
Unde : Ω este un tensor de ordinal doi antisimetric .
Se numeste tensorul viteza unghiulara .
Exista in matematica o teorema , numita teorema de reprezentare al carui enunt este urmatorul :
Pentru orice tensor Ω de ordinul z antisimetric exista si este unic un
vector ω astfel incat
![]()
Utilizand aceasta teorema
relatia (12) devine ![]() (13)
(13)
unde ![]() - se numeste vectorul viteza
unghiulara si este definit ca fiind :
- se numeste vectorul viteza
unghiulara si este definit ca fiind :
![]() (14)
(14)
unde ωx , ωy , ωz sunt cei definiti de realatia (8) :
Relatia (6) devine ![]() (15)
(15)
numita si relatia lui Euler pentru distributia de viteze.
In fapt aceasta relatie este o functionala , numita functionala vitezei :
![]() (16)
(16)
unde t reprezinta campul si ![]() campul sau distributia .
campul sau distributia .
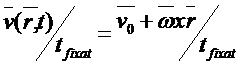 (17) se numeste
distributie de viteze si inseamna vitezele tuturor punctelor la
un moment dat de timp .
(17) se numeste
distributie de viteze si inseamna vitezele tuturor punctelor la
un moment dat de timp .
DISTRIBUTIA ACCELERATIILOR
Functionala vectorului acceleratie se obtine prin derivarea in raport cu timpul a functionalei vectorului viteza (relatia 16).
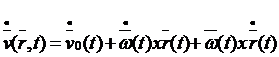
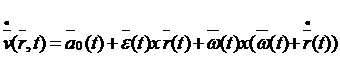 (19)
(19)
Unde au fost notate :
![]() si se
numeste accelratia lui O .
si se
numeste accelratia lui O .
![]() si se numeste
accelratia unghiulara .
si se numeste
accelratia unghiulara .
Se obtine functionala acceleratiei de forma :
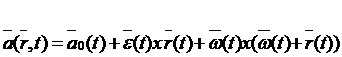
Pentru un moment de timp t fixat se obtine distributia de acceleratie , adica acceleratiile tuturor punctelor solidului la un moment dat .
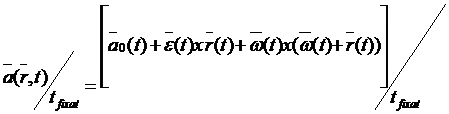
Aceasta relatie mai este cunoscuta si sub numele de formula lui Euler pentru distributia de acceleratii .
Observatie . Daca ne intereseaza viteza sau
acceleratia unui anume punct , atunci recalculam 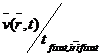 , respectiv
, respectiv 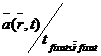 . Acestea sunt viteza , respectiv
accelerata definite la studiul miscarii punctului .
. Acestea sunt viteza , respectiv
accelerata definite la studiul miscarii punctului .
Facand analogie intre functionala vitezei si expresia variatia momentului unei forte in raport cu polul de reducere .
![]()
si
![]()
Constatam ca pe pozitia lui ![]() se afla
se afla ![]() , iar in pozitia lui
, iar in pozitia lui ![]() se afla
se afla ![]()
In cazul reducerii sistemelor de forte
ne aducem aminte ca pentru valori particulare ale lui ![]() si
si ![]() rezultau diferite cazuri de reducere .
rezultau diferite cazuri de reducere .
Prin analogie , in functie de anumite
valori particulare ale lui ![]() si
si ![]() rezulta anumite miscari particulare ale solidului rigid (tabelul
1 ).
rezulta anumite miscari particulare ale solidului rigid (tabelul
1 ).
Tabelul 1 . Miscari particulare ale solidului rigid.
|
Definitie cinematica |
Definitie generala |
|||
|
REPAUS |
|
Toate punctele solidului rigid raman fixe in spatiu |
||
|
TRANSLATIE |
|
Orice dreapta a solidului rigid ramane paralela cu ea insasi |
||
|
|
ROTATIE CU PUNCT FIX |
|
Un punct al solidului rigid ramane fix in spatiu |
|
|
ROTATIE CU AX FIX |
|
Doua puncte ale solidului rigid raman fixe in spatiu |
||
|
ROTO-TRANSLATIE |
|
O dreapta solidului rigid ramane fixa in spatiu |
||
|
PLAN-PARALELA |
|
Trei puncte ale solidului rigid raman tot timpul in planul initial |
||
|
GENERALA |
|
MISCARI PARTICULARE ALE SOLIDULUI RIGID
MISCAREA DE TRANSLATIE
Un solid rigid efectueaza o miscare de translatie , daca o dreapta a corpului ramane paralela cu ea insasi tot timpul miscarii ( figura 1).
Definitia cnematica : ![]()
![]()
![]() 0 ,
0 , ![]() t
t
Conform definitiei
geometrice a moscarii , axele Ox , Oy , Oz ale sistemului de
referinta mobil raman paralele cu ele insele si paralele cu
niste directii fixe din spatiu (de exemplu cu axele O1x1
, O1y1 si O1z1 ) . In aceste
conditii , versorii ![]() ,
, ![]() ,
, ![]() , raman
constanti iar derivatele lor in raport cu timpul sunt nule .
, raman
constanti iar derivatele lor in raport cu timpul sunt nule .
![]()
![]()
![]() =0
=0
Relatia (1) este satisfacuta numai daca :
![]() (2)
(2)
Deci si ![]() =0
=0
Formulele lui Euler pentru distributiile de viteze si de acceleratie devin .
![]() (3)
(3)
![]()
Daca punctele solidului rigid descriu traiectorii liniare (rectilinii) atunci translatia se numeste translatie rectilinie .
Daca traiectoriile punctelor solidului rigid descriu sunt arce de cerc, atunci translatia este translatie circulara.
Daca traiectoriile punctelor solidului sunt curbe , atunci translatia este translatie curbilinie .
MISCAREA DE ROTATIE CU AXA FIXA
Un solid rigid efectueaza o miscare de rotatie cu axa fixa , daca in timpul miscarii doua puncte ale rigidului raman fixe in spatiu (figura 2) .
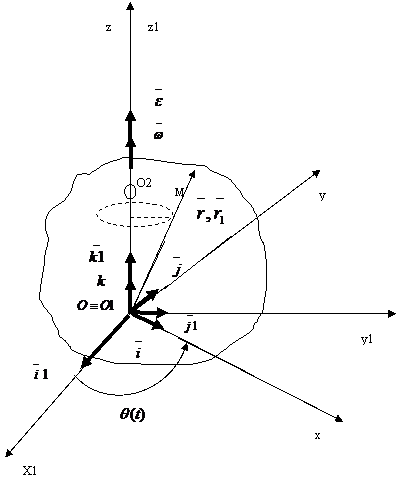
Se presupun punctele fixe O1 si O2 . Axa care uneste cele doua puncte fixe se numeste axa de rotatie si toate punctele ei raman fixe in timpul miscarii . Se aleg sistemele de referinta fix si mobil , astfel incat originile O1 si O sa coincida , iar axele O1z1 si Oz sa se suprapuna pe axa de rotatie a corpului .
Miscarea rigidului este definita daca se cunoaste functia scalara :
θ = θ(t) , (4)
θ fiind unghiul format de axele Ox si O1x1 , respectiv Oy si O1y1 din planul perpendicular pe axa de rotatie .
Pozitia unui punct oarecare M al corpului este definita de vectorul de pozitie .
![]() , (5)
, (5)
deoarece ![]() si deci
si deci ![]() si
si ![]() (
( ![]() )
)
Punctele corpului descruiu traiectorii circulare , in plane normale pe axa de rotatie , cu centrul pe aceasta axa .
Intre versorii sistemului de referinta mobil si cei ai sistemului de referina fixa exista urmatoarele relatii :
![]()
![]() (6)
(6)
![]()
Prin derivarea acestor relatii in raport cu timpul, se obtin:
![]()
![]()
![]()
In baza relatiilor prin care am definit
proiectiile pe axe ale vectorului viteza unghiulara ![]() obtinem:
obtinem:
![]()
![]()
![]()
si in continuare:
![]() (9)
(9)
![]() (10)
(10)
Rezulta ca vectorul ![]() are o interpretare fizica bine precizata . Acest vector are
directia axei de rotatie si marimea egala cu viteza
unghiulara
are o interpretare fizica bine precizata . Acest vector are
directia axei de rotatie si marimea egala cu viteza
unghiulara ![]() . Vectorul
. Vectorul ![]() , acelasi pentru toate punctele rigidului , se numeste vector
viteza unghiulara .
, acelasi pentru toate punctele rigidului , se numeste vector
viteza unghiulara .
Prin derivarea in raport cu timpul a relatiei (9) se obtine vectorul acceleratie unghiulara , acelasi pentru toate punctele corpului
![]() (11)
(11)
In aceste conditii , distributia vitezelor in miscarea de rotatie cu ax fix este :
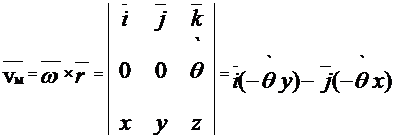 (12)
(12)
![]()
![]()
![]()
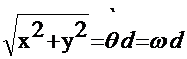 (14)
(14)
Distributia acceleratiilor in miscarea de rotatie cu ax fix este:
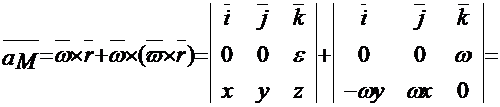
![]()
![]() (15)
(15)
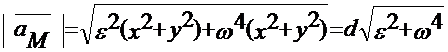 (16)
(16)
PROPRIETATI ALE DISTRIBUTIEI DE VITEZE SI DE ACCELERATIE IN MISCAREA DE ROTATIE
In miscarea de rotatie exista puncte de viteza si acceleratie nula . Aceste puncte se afla pe axa de rotatie .
Punctele situate pe o dreapta paralela cu axa de rotatie au aceeasi viteza si aceeasi acceleratie .
Pe o dreapta perpendiculara pe axa de rotatie vitezele variaza liniar , deoarece marimea vitezei este proportionala cu distanta d de la un punct la axa . Vitezele tuturor punctelsor sunt paralele intre ele si perpendiculare pe dreapta .
pe o dreapta perpendiculara pe axa de rotatiei accelertiile variaza liniar si sunt inclinate fata de aceasta dreapta cu acelasi unghi α pentru care .
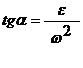
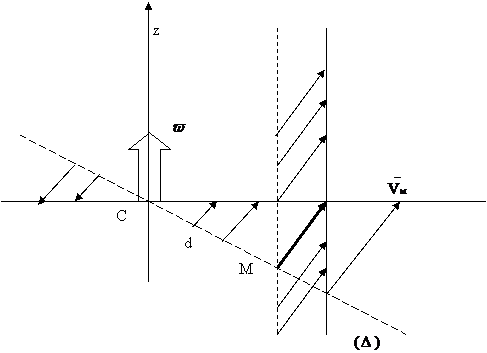
Fig. 3
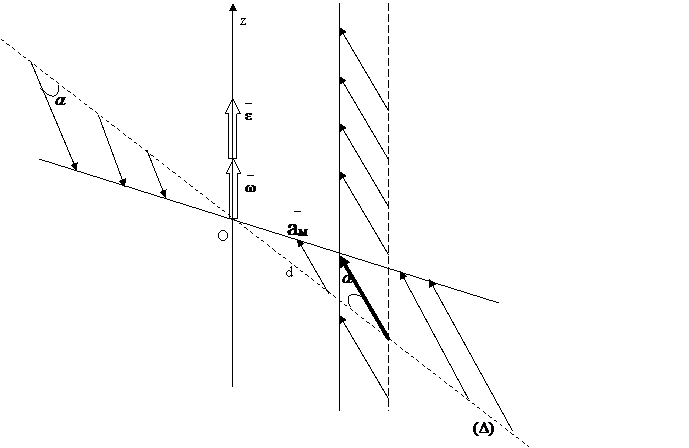 Fig. 4.
Fig. 4.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1783
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved