| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
ECHILIBRUL SOLIDULUI RIGID
7. 1. Echilibrul solidului rigid liber
|
|
Se considera un solid rigid
actionat de un sistem de n forte ![]() , i = 1, .n (fig. 7.1).
, i = 1, .n (fig. 7.1).
Solidul rigid liber poate sa ocupe orice pozitie in spatiu, nu este ingradit de nici o obligatie geometrica.
Sistemul de forte este echivalent intr-un punct oarecare O al rigidului cu torsorul acestuia , adica :

Fig. 7.1

Conditia necesara si suficienta ca solidul rigid sa fie in echilibru este ca
rezultanta ![]() si momentul rezultantei
si momentul rezultantei ![]() sa fie egali cu zero .
sa fie egali cu zero .
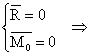
Cele 2 relatii vectoriale (2) sunt echivalente cu urmatoarele 6 ecuatii scalare :
![]()
![]()
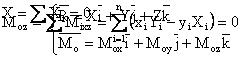
considerand ca :
Probleme posibile :
se dau complet fortele - se cere pozitia de echilibru;
se da pozitia de echilibru - se cer fortele;
se da partial pozitia de echilibru, partial sistemul de forte - se cer complet fortele si complet pozitia de echilibru;
![]()
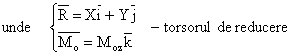
Pentru un rigid liber actionat de forte plane, conditia de echilibru este :
![]()
Un solid rigid liber actionat de forte in spatiu are 6 grade de libertate (fig. 7.2).
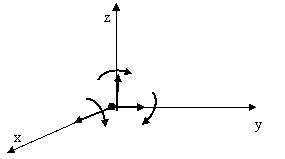
trei translatii si trei rotatii
Fig. 7.2
|
|
Un solid rigid actionat de forte in plan are 3 grade de libertate (fig. 7.3).
2 translatii + 1 rotatie
Fig. 7.3
5. 2. Echilibrul solidului rigid cu legaturi fara frecare
Legatura este o obligatie geometrica pe care o are unul sau mai multe puncte ale rigidului .
Un solid rigid liber poseda 6 grade de libertate (3 rotatii + 3 translatii).
Legaturile pot rapi posibilitati de translatie sau de rotatie sau combinatii de translatii si rotatii.
Legaturile uzuale ale solidului rigid :
a) - reazem simplu (un singur punct de contact)
b) - articulatie
c) - incastrare
d) - legatura prin fire
Si in cazul rigidului este valabila axioma legaturii - orice legatura se poate inlocui cu o forta de legatura (reactiune) sau un sistem de forte de legatura .
a) Reazem simplu
|
|
Un solid rigid are intr-un punct al sau un reazem simplu daca este obligat sa ramana tot timpul pe o suprafata (fig. 7.4).
A - punct de contact
Σ - suprafata rigida nedeformabila
Simpla
rezemare se inlocuie cu o reactiune normala ![]() ,
avand directia ┴ pe cele 2 suprafete in contact .
,
avand directia ┴ pe cele 2 suprafete in contact .
Exemplu :
|
|
|
|
O asemenea legatura asigura corpului 5 grade de libertate .
|
|
Simbol :
b) Articulatia
Dupa modalitatea de realizare practica, articulatia poate fi sferica sau cilindrica .
|
|
b1) - Articulatia sferica - suprima corpului 3 grade de libertate, lasand posibile numai rotatiile corpului in raport cu 3 axe rectangulare care trec prin centrul articulatiei (fig. 7.5).
asigura rigidului un punct fix
|
|
o articulatie sferica se inlocuieste cu o reactiune de directie si marime oarecare .
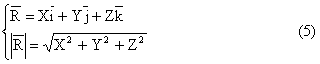
Fig. 7.5
b2) - Articulatia cilindrica asigura rigidului o directie fixa . Corpul are 2 grade de libertate , rotatia si translatia in raport cu directia fixa (fig. 7.6).
|
|
2 grade de libertate
Fig. 7.6
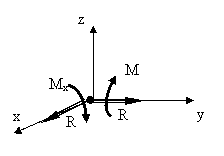

Articulatia cilindrica se inlocuie cu torsorul de reducere format din ![]() si
si ![]() (fig. 7.7) cu:
(fig. 7.7) cu:
Fig. 7.7 - schema reactiunilor
|
|
Simbol :
|
|
Observatie : Daca fortele care actioneaza asupra rigidului sunt forte coplanare, atunci articulatia este inlocuita cu o reactiune (fig. 7.8) :
![]()
Fig. 7.8
c) Incastrarea - este legatura care suprima rigidului toate gradele de libertate (fig. 7.9).
Incastrarea se inlocuie cu torsorul fortelor de legatura .
A ![]() - rezultanta
- rezultanta
![]() - vector moment rezultant
- vector moment rezultant

iar modulele pentru ![]() si
si ![]() sunt:
sunt:
![]() (9)
(9)
![]() (10)
(10)
|
|
Fig. 7.9
Exemplu (fig. 7.10):
|
|
Fig. 7.10
|
|
d) Legatura prin fir suprima rigidului un grad de libertate . In fir ia nastere o forta de legatura denumita tensiune (fig. 7.11)
![]() - directie - dreapta dupa care este intins
firul
- directie - dreapta dupa care este intins
firul
- sens - dirijat de la rigid la punctul de ancorare al firului .
Fig. 7.11
Conditia necesara si suficienta ca rigidul supus la legaturi fara frecare sa fie in echilibru este ca:

unde: ![]() ,
,
![]() - torsorul fortelor efectiv aplicate solidului
- torsorul fortelor efectiv aplicate solidului
![]() ,
,
![]() '-
torsorul fortelor de legatura in raport cu acelasi pol (punct de reducere) .
'-
torsorul fortelor de legatura in raport cu acelasi pol (punct de reducere) .
5. 3. Echilibrul solidului rigid cu legaturi cu frecare
In cazul solidului rigid se manifesta urmatoarele tipuri de frecari :
- frecarea de alunecare pentrul rigidul simplu rezemat
La eliberarea
corpului de legaturi se introduce o forta de legatura denumita forta de frecare
de alunecare notata cu ![]() cu urmatoarele proprietati :
cu urmatoarele proprietati :
directia - situata in planul tangent la suprafetele in contact
sens - invers ( contrar ) tendintei de miscare
modul - | ![]() | ≤ μ│
| ≤ μ│![]() │ la echilibru (12)
│ la echilibru (12)
- │![]() │=
μ│
│=
μ│![]() │ pentru miscare (13)
│ pentru miscare (13)
μ - coeficient de frecare la alunecare (determinat experimental). Este o marime adimensionala.
![]() - reactiunea normala in punctul de contact la
planul tangent comun .
- reactiunea normala in punctul de contact la
planul tangent comun .
- frecarea de rostogolire se manifesta in cazul reazemului simplu ca urmare a microdeformatiilor suprafetelor in contact. Apare in miscarea de rostogolire sau in tendinta de a se produce o asemenea miscare a unui rigid.
Se considera o roata care se deplaseaza cu frecare pe o suprafata plana (fig. 7.12).
|
|
A - punct ideal de contact
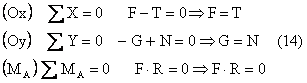
Alegand un sistem de axe xOy la echilibru putem
scrie :
Fig. 7.12
Din ultima relatie, cum R ≠ 0 ( raza ) => F = 0
Experimental roata este in echilibru si pentru valori ale lui F ≠ 0 .
Analizand neconcordanta intre teorie si practica se ajunge la concluzia ca trebuie renuntat la ipoteza rigiditatii (conform careia contactul dintre roata si suprafata de sprijin are loc intr-un singur punct A) si trebuie luata in considerare situatia reala conform careia atat roata cat si calea de rulare, admit o deformatie limitata, contactul lor realizandu-se pe o anumita suprafata (pata de contact) in jurul punctului A (fig. 7.13) .
|
|
Fig. 7.13 Fig. 7.14
Pentru a
avea concordanta intre teorie si practica se introduce momentul de frecare de
rostogolire![]() opus sensului de rostogolire
sau tendintei de rostogolire .
opus sensului de rostogolire
sau tendintei de rostogolire .
![]() : - directie - perpendicular pe planul
determinat de
: - directie - perpendicular pe planul
determinat de ![]() si
si
![]()
- sens contrar tendintei de rostogolire
- modul │![]() │≤
s│
│≤
s│![]() │
- la echilibru (15)
│
- la echilibru (15)
unde :s = xmax conform figurii 7.14
Mr = xN (16)
Mr max = sN (17)
s - "coeficient" de frecare de rostogolire.
Are dimensiunea unei lungimi (se determina experimental).
Exemplu: - pentru roata de vagon R = 0,5 m
s= (0,050 - 0,055) cm
- rulmenti cu bile s = (0,0015 - 0,0050) cm
Coeficientul
de frecare de rostogolire se poate calcula cu relatie aproximativa: ![]() (R-raza rotii)
(R-raza rotii)
Schema corecta (repartitia) a fortelor efectiv aplicate si a celor de legatura pentru o roata este conform figurii 7.15:
|
|
Fig. 7.15
Conditia necesara si suficienta ca un solid rigid supus la legaturi cu frecare sa fie in echilibru este ca Σ dintre torsorul fortelor efctiv aplicate si torsorul fortelor de legatura sa fie zero .
7.4. Echilibrul sistemelor de corpuri (solide rigide)
Prin sistem de corpuri (solide rigide) intelegem mai multe corpuri legate intre ele prin legaturi mecanice (articulatii, reazeme simple, incastrari) care suprima partial sau total gradele de libertate ale sistemului .
|
|
Se considera sistemul de corpuri din figura 7.16 articulate intre ele in B si C si legate prin articulatia A si reazemul D de o suprafata.
A - articulatie
D - reazem simplu
B , C - articulatie
Asupra sistemului de corpuri actioneaza sistemul de forte:
![]() .
. ![]() .
.
![]() si
si ![]() necunoscute
necunoscute
In B si C apar reactiuni interioare perechi , egale si de sensuri contrare :
![]()
Metode de rezolvare a echilibrului corpurilor :
a) - metoda izolarii corpurilor
b) - metoda solidificarii
c) - metoda echilibrului partilor
a) Metoda izolarii corpurilor - se bazeaza pe faptul ca daca un sistem de corpuri este in echilibru, atunci fiecare corp al sistemului trebuie sa fie in echilibru .
b) Metoda solidificarii - se bazeaza pe teorema solidificarii - daca fiecare corp din sistem se afla in echilibru sub actiunea fortelor exterioare si de legatura, atunci si sistemul in ansamblu se afla in echilibru .
c) Metoda echilibrului partilor - se bazeaza pe teorema echilibrului partilor - daca fiecare corp se afla in echilibru sub actiunea fortelor aferente lui, anumita parti din sistem vor fi de asemenea in echilibru.
Metoda de rezolvare a unei probleme de sistem de corpuri este urmatoarea :
se descompune sistemul de corpuri, eliberand fiecare corp de legaturi, inlocuind legaturile cu reactiunile corespunzatoare;
se scriu ecuatiile de echilibru pentru fiecare corp in parte;
se rezolva sistemul de ecuatii astfel obtinut, rezultand reactiunile exterioare si interioare
Date :
O2 , O5 - articulatii
A - reazem simplu
G - reazem
B - incastrare
P , Q2 , G , Q4 , Q5
O5O2= 2l O2A = 3l/2
EB = 2l α
ED = l/2
Se cere :
P = ? pentru echilibru
reactiunile din O5 , O2 , A , D , B
|
|
Fig. 7.17
 Se
aplica metoda izolarii corpurilor
Se
aplica metoda izolarii corpurilor
1) ![]()
|
|
2)

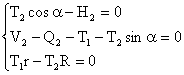
|
|
3)

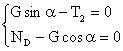
4)
|
|

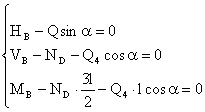
5)
|
|

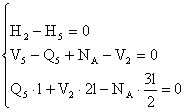
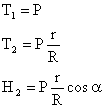
![]()
![]()

![]()
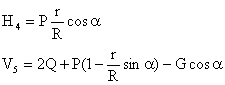
![]()
Aplicatia 2 (fig. 7.18)
|
|
F = ?
|
|

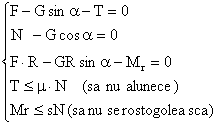

Notam ![]()
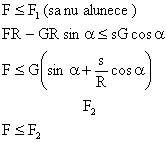
a) ![]()
![]()
b) ![]()
![]()
![]()
![]() c)
c)
![]()
|
|

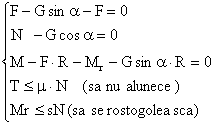
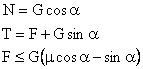
![]()
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6278
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved