| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Marimi fizice. Unitati de masura. Dimensiuni
Efectuarea unei operatii de masurare a
oricarei marimi fizice M implica
stabilirea unei unitati
de masura corespunzatoare. Subliniem ca alegerea
unitatii de masura nu rezulta din nici o lege a fizicii, ci este determinata de
factori ca: cerintele impuse de practica, reproductibi-litate, consens general etc. Orice marime
fizica M trebuie
exprimata prin produsul dintre valoarea numerica si unitatea de masura
![]() M
M ![]()
M =![]() M
M![]()
Deoarece, pentru o marime fizica M se pot utiliza mai multe unitati de
masura, se obtine:
M
= ![]() M 1,
M 1, ![]() =
= ![]() M 2
M 2![]() (1.2)
(1.2)
de unde
/=![]() M 1
M 1![]()
![]() M 2
M 2![]() (1.3)
(1.3)
Adica, raportul valorilor numerice ale unei marimi fizice este egal cu inversul raportului unitatilor de masura.
Exprimarea marimilor fizice sub forma unui produs de forma (1.1), conduce la o deosebire dintre formulele fizice si cele matematice. De exemplu, daca avem un patrat cu latura X, atunci din punctul de vedere al matematicii, aria patratului este A = X2, iar din punctul de vedere al fizicii, trebuie sa scriem:
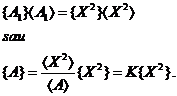
Asadar, in formulele fizice poate aparea un coeficient parazit K, exprimat prin raportul unitatilor de masura. Aceasta a condus la necesitatea practica de elaborare a unui sistem de unitati coerent, astfel incat in formulele fizice coeficientul parazit sa fie K = 1.
In sistemul coerent de unitati de masura, Sistemul International (SI), se disting trei clase de marimi fizice si unitati de masura corespunzatoare: 1. Marimi fizice si unitati de masura fundamentale; 2. Marimi fizice si unitati de masura suplimentare si 3. Marimi fizice si unitati de masura derivate.
Tabelul 1.1 Marimi fizice si unitati de masura fundamentale
|
Marimea fizica |
Simbolul marimii fizice |
Unitatea de masura |
Simbolul unitatii de masura |
||
|
1 |
Lungimea |
L |
metrul |
m |
|
|
2 |
Timpul |
T |
secunda |
s |
|
|
3 |
Masa |
M |
kilogram |
kg |
|
|
4 |
Temperatura termodinamica |
Θ |
grad Kelvin |
K |
|
|
5 |
Intensitatea curentului electric |
I |
Amper |
A |
|
|
6 |
Cantitatea de substanta |
ν |
mol |
mol |
|
|
7 |
Intensitatea luminoasa |
I |
candela |
cd |
|
|
Tabelul 1.2. Marimi fizice si unitati de masura suplimentare |
|||||
|
Marimea fizica |
Simbolul marimii fizice |
Unitatea de masura |
Simbolul unitatii de masura |
||
|
1 |
Unghiul plan |
α |
radian |
rad |
|
|
2 |
Unghiul solid |
Ω |
steradian |
sr |
|
![]()
![]()
Coerenta sistemului
international consta in faptul ca unitatile de
masura pentru marimile fizice derivate se exprima numai
si numai sub forma unor combinatii ale unitatilor de
masura fundamentale sau suplimentare. Ilustram aceasta
afirmatie prin cateva exemple - viteza liniara ![]() v
v![]() =m/s, acceleratia
=m/s, acceleratia ![]() a
a![]() = m/s2 ,
= m/s2 ,
viteza unghiulara ![]() ω
ω![]() = rad/s si acceleratia unghiulara
= rad/s si acceleratia unghiulara ![]() ε
ε![]() = ad/s2.
= ad/s2.
In afara de valoarea
numerica , respectiv unitatea de masura ![]() M
M ![]() , orice marime fizica se caracterizeaza
si prin dimensiunea [M], care
reprezinta un monom algebric de puteri - pozitive, negative, intregi sau
fractionare - ale simbolurilor marimilor fizice fundamentale sau
suplimentare:
, orice marime fizica se caracterizeaza
si prin dimensiunea [M], care
reprezinta un monom algebric de puteri - pozitive, negative, intregi sau
fractionare - ale simbolurilor marimilor fizice fundamentale sau
suplimentare:
![]() (1.5)
(1.5)
Dimensiunea [M] are un rol fundamental in verificarea corectitudinii formulelor fizice.
In Sistemul International (SI), unitatea de masura pentru forta este Newtonul
![]()
Daca unitatile de masura pentru masa, lungime si timp se exprima in sistemul de unitati GCS (centimetru, gram, secunda), avem:
![]()
Definitiile unitatilor de masura in sistemul international
Unitatile de masura pentru marimile fizice fundamentale si suplimentare pot fi stabilite in doua moduri diferite:
a) Pe baza unor considerente de ordin practic, se fixeaza unitati de masura arbitrare prin elaborarea de etaloane corespunzatoare.
b) Se alege ca unitate de masura valoarea unei marimi fizice existente in natura. De exemplu, se poate stabili ca unitate de lungime distanta dintre atomii vecini ai unui cristal, ca unitate de masa cea a atomilor de hidrogen etc. Avantajul unor astfel de unitati naturale consta in reproductibilitatea lor.
La inceputul elaborarii unitatilor de masura s-a mers pe prima varianta, dar pe masura dezvoltarii fizicii atomice si nucleare au fost stabilite unitati de masura naturale pentru marimile fizice.
Redam definitiile actuale pentru unitatile de masura ale marimilor fizice fundamentale si suplimentare:
Unitatea de lungime (metrul). Metrul este lungimea egala cu 1.650.763,73 lungimi de unda in vid a radiatiei care corespunde tranzitiei intre nivelele de energie 2pl{) si 5d5 ale atomului de kripton 86 (3686 Kr).
Unitatea de timp (secunda). Secunda este durata a 9.192.631.770 perioade ale radiatiei care corespunde tranzitiei intre cele doua nivele hiperfine de energie ale starii fundamentale a atomului de cesiu 133 ( 36Cs).
Unitatea de masa (kilogramul). Prototipul international al kilogramului ramane cel confectionat cu prilejul primei conferinte generale de masuri si greutati, din anul 1889. Acest prototip international din platina iridiata se pastreaza la Biroul International de Masuri si Greutati in conditiile stabilite in anul 1889.
Unitatea de intensitate a curentului electric (amperul). Amperul este intensitatea unui curent electric continuu care, mentinut in doua conductoare paralele rectilinii cu lungime infinita si cu sectiunea circulara neglijabila, asezate in vid la o distanta de 1 m unul de altul, produce intre aceste conductoare o forta egala cu 2-10' N, pe o lungime de 1 m.
Unitatea de temperatura termodinamica (gradul Kelvin). Gradul Kelvin, ca unitate de temperatura termodinamica, este fractiunea 1/273,16 din temperatura termodinamica a punctului triplu al apei.
Unitatea cantitatii de substanta (molul). Aceasta unitate de masura fundamentala a fost adoptata la A 14-a Conferinta Internationala de Masuri si Greutati din anul 1971. Prin rezolutia 3 a acestei conferinte se specifica:
Molul este cantitatea de substanta a unui sistem care contine atatea entitati elementare, cati atomi exista in 0,012 kilograme de carbon 12 ('6C). Masa de 0,012 kg de carbon 12 contine un numar de atomi egal cu numarul lui Avogadro (N = 6,022-IO23 mol'1 ).
De cate ori se utilizeaza molul, entitatile elementare trebuie specificate, ele putind fi atomi, molecule, ioni. alte particule sau grupuri de particule.
Unitatea de intensitate luminoasa (candela). Candela este intensitatea luminoasa, in directia normalei, a unei suprafete cu aria 1/600.000 metri patrati a unui corp negru la temperatura de solidificare a platinei si presiunea de 101325 Newton pe metru patrat.
Subliniem ca unitatile de masura pentru marimile fizice fundamentale, precum si numarul acestor marimi, nu se considera stabilite definitiv prin definitiile enuntate mai sus.
Unitatile de masura suplimentare se definesc in felul urmator:
Unitatea de unghi plan (radianul). Radianul este unghiul plan cuprins intre doua raze care delimiteaza pe circumferinta unui cerc un arc de lungime egala cu cea a razei (fig. 1.1). Unghiul de un radian este egal cu I8O/71 grade sexagesimale, adica 1 rad = 5717'45'.
Unitatea de unghi solid (steradianul). Steradianul este unghiul solid care, avand varful in centrul unei sfere, delimiteaza pe suprafata acestei sfere o arie egala cu aria unui patrat de latura egala cu raza sferei.
|
|
|
|
|
kf(x) |
Fig. 1.1
Fig.1.2
Fig.1.3
Daca din centrul unei sfere de raza /* se traseaza o suprafata conica (fig.1.2), atunci aceasta suprafata intersecteaza o parte din sfera, aria acestei parti fiind proportionala cu /' si cu valoarea unghiului solid AQ. Astfel:
![]() .
.
Este evident ca acest raport nu depinde de raza sferei.
Unghiul solid
total sub care se vede suprafata sferica, din centrul sferei, este: ![]()
Atat radianul, cat si steradianul sunt unitati de masura adimensionale.
Alte unitati de masura. Ordine de marime
S-a constatat necesitatea utilizarii unor unitati de masura care, desi nu fac parte din SI, joaca un rol important si sunt larg raspandite. Unele dintre aceste unitati de masura sunt indicate in tabelul 1.3.
Se recomanda ca astfel de unitati de masura, tolerate de sistemul international sa fie folosite cat mai rar posibil.
Sunt admise si unele unitati de masura a caror folosire este utila in diferite domenii de activitate ca, de exmplu:
Electron-volt (eV). Un electron-volt este energia cinetica castigata de un electron care traverseaza - in vid - o diferenta de potential de un volt: 1 eV≈1,60219*10-19 J.
Unitatea atomica de masa (u.a.m.). Unitatea atomica de masa este fractiunea 1/12 din masa unui atom al izotopului carbon 12 ( 6C): 1 u= 1,66057* kg.
Tabelul 1.3. Unele unitati de masura folosite impreuna cu unitatile SI
|
Denumirea |
Simbol |
Valoarea in SI |
|
An |
a |
la = 3,16-107s |
|
Zi |
d |
1 d = 24 h = 1440 min = 86400 s |
|
Ora |
h |
i h = 60 min = 3600 s |
|
Minut |
min |
1 min = 60 s |
|
Grad |
o |
1 = ti/180 rad |
|
Minut |
|
1' =(1/60) = (n/10800) rad |
|
Secunda |
|
1' = (1/60)' = (ti/648000) rad |
|
Litru |
|
1 l=l-dm3=10'3m'3 |
|
Tona |
t |
1 t= IO3 kg |
in fizica atomica si nucleara, lungimile se exprima in unitati ca Angstrom (A) si Fermi (f): 1 A = 10'l() m; 1 f = 10'i5 m.
Unitatile de masura pentru lungimi, utilizate in mod obisnuit in astronomie, sunt:
unitatea astronomica (UA) - egala cu distanta medie dintre Soare si Pamant: 1UA= 1,495980-10' m;
anul lumina (al), egal cu distanta pe care o parcurge lumina in vid, in decursul unui an: 1 al = 9,4605-l015 m;
unitatea de masura denumita parsec (ps) sau secunda paralaxica este distanta de la care raza orbitei de revolutie a Pamantului in jurul Soarelui apare sub unghiul de paralaxa egal cu o secunda (1'): 1 ps = 206264,8 UA = 3,26169 al = 3,0875-IO16 m.
Multiplele date experimentale au scos in evidenta faptul ca dimensiunile, duratele si masele pentru sistemele existente in natura au valori cuprinse in game extrem de largi. Exemple ale ordinelor de marime pentru lungime, timp si masa sunt date in urmatoarele trei tabele.
Tabelul 1.4. Ordine de marime pentru lungime
|
Obiectul masurat |
Lungimea (m) |
Obiectul masurat |
Lungimea (m) |
|
Distante intergalactice |
IO25 |
Lungimea de unda pentru o linie spectrala a sodiului |
|
|
Raza Galaxiei |
IO21 |
||
|
Distanta Pamant - Soare |
|
Constanta retelei cristaline (Ag) |
|
|
Raza Pamantului |
|
Raza atomului de hidrogen |
|
|
Obiecte utilizate in tehnica |
10'*-MO5 |
Raza protonului |
0,8-10 i5 |
Tabelul 1.5. Ordine de marime pentru timp
|
Obiectul masurat |
Timpul (s) |
Obiectul masurat |
Timpul (s) |
|
Varsta Universului (ipoteze) |
|
Perioada de rotatie diurna a Pamantului |
8,6-IO4 |
|
Varsta Pamantului |
l,5-1017 |
Perioada satelitilor |
2,4- IO3 |
|
Organisme biologice |
MO17 |
Perioadele oscilatiilor mecanice |
~ IO''1 |
|
Piramida lui Keops |
|
Perioada rotatiilor moleculare |
|
|
Perioada de revolutie a Pamantului |
3,2-IO7 |
Perioada luminii |
IO'1* |
|
Perioada de revolutie a Lunii |
2,4-IO6 |
Perioada oscilatiilor nucleare |
|
|
Intervale de timp cu aplicatii tehnice |
10'VlO' |
Timpul elementar (ipoteze) |
IO''4 |
Tabelul 1.6. Ordine de marime pentru masa
|
Obiectul masurat |
Masa (kg) |
Obiectul masurat |
Masa (kg) |
|
Universul (ipoteze) |
1O'J |
Obiecte de utilizare tehnica |
lO^'-rlO' |
|
Galaxia |
2-IO41 |
Virusi |
|
|
Soarele |
2-IO30 |
Protonul |
1,7-IO'27 |
|
Pamantul |
6-IO24 |
Electronul |
9-IO-11 |
Tabelul 7.7. Prefixele factorilor de multiplicare
|
Factorul de multiplicare |
Denumirea prefixului |
Simbolul prefixului |
Factorul de multiplicare |
Denumirea prefixului |
Simbolul prefixului |
|
toIM |
exa |
E |
|
deci |
d |
|
|
peta |
P |
10'J |
centi |
c |
|
|
tera |
T |
|
mili |
m |
|
|
giga |
G |
|
micro |
u |
|
l(f |
mega |
M |
10y |
nano |
n |
|
ios |
kilo |
k |
10'1J |
pico |
P |
|
|
hecto |
h |
io-3 |
femto |
f |
|
|
deca |
da |
|
atto |
a |
Datorita acestor game extrem de largi pentru valorile marimilor fizice, la Cea de-a 11 -a Conferinta Generala de Marimi si Greutati, din anul 1960, s-au stabilit denumiri si simboluri pentru prefixe, destinate formarii multiplilor si submultiplilor unitatilor fundamentale din Sistemul International. Tabelul prefixelor a fost completat in anul 1964, respectiv in anul 1975. Denumirea si simbolurile pentru prefixele adoptate sunt date in tabelul 1.7.
Erori de masurare
Valorile marimilor fizice se obtin in diverse procese de masurare. Datele experimentale arata ca nu este posibila efectuarea unei masurari absolut exacte. Nu ne vom ocupa de erorile experimentale sistematice, datorate unor etalonari gresite ale aparatelor de masura sau utilizarea unor metode de masurare inadecvate, ci numai de erorile intamplatoare.
Erorile intamplatoare ale masurarilor individuale sunt inevitabile, dar prin combinarea mai multor masurari erorile intamplatoare pot fi substantial reduse. Orice masurare este afectata de eroarea absoluta:
![]()
si de eroarea relativa
![]()
unde xm este valoarrea masurata, iar xr este valoarea reala a marimii fizice X.
Daca se efectueaza un numar n de masurari directe si succesive asupra marimii fizice X, cu mijloace si metode de masurare adecvate, se obtin valorile individuale:
![]()
Fiecare valoare individuala este afectata de eroarea absoluta
![]()
si de eroarea relativa
![]()
Erorile intamplatoare influenteaza rezultatele masurarilor succesive in ambele sensuri, ceea ce conduce la faptul ca valorile individuale xi vor fi cand mai mici, cand mai mari decat valoarea reala xr. Subliniem ca obtinerea rezultatelor individuale putin diferite unele de altele sau a unor rezultate care coincid intre ele este o consecinta logica a conditiilor de masurare. Daca prin repetarea masurarilor se obtin riguros aceleasi valori individuale, inseamna ca metoda de masurare utilizata nu este suficient de sensibila.
Tabelul 1.8. Rezultatele experimentale obtinute de catre Michelson
|
Viteza luminii c, (km/s) |
Numarul de aparitii n, |
Viteza luminii c, (km/s) |
Numarul de aparitii ni |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
De exemplu, in tabelul 1.8 se indica rezultatele celor 100 de masurari succesive ale vitezei luminii in vid, obtinute de catre Michelson in anul 1879.
Scopul efectuarii oricarei masurari consta in stabilirea valorii reale xr . Se arata ca valoarea reala xr poate fi estimata prin valoarea medie a setului de masurari (1.15)
![]() (1.18)
(1.18)
Se constata distributia setului de masurari (1.15) in jurul valorii medii x , iar abaterea standard sau dispersia rezultatelor experimentale individuale este data de marimea:
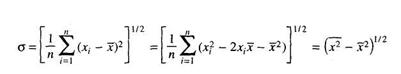
|
|
Valorile individuale ale unui set de n masurari, daca n este suficient de mare, se distribuie dupa densitatea de repartitie Gauss sau densitatea repartitiei normale:
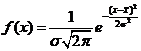
(1.21)
Produsul /(jc) reprezinta probabilitatea ca in urma efectuarii unei masurari sa se obtina o valoare cuprinsa intre x si x + dx . Se verifica simplu egalitatea:
![]() Aceasta
egalitate indica faptul ca obtinerea unui rezultat oarecare este
o certitudine, adica are loc cu probabilitatea P = 1.
Aceasta
egalitate indica faptul ca obtinerea unui rezultat oarecare este
o certitudine, adica are loc cu probabilitatea P = 1.
|
|
Densitatea de repartitie Gauss se reprezinta grafic ca in figura 1.3, fiind cunoscuta sub denumirea de clopotul lui Gauss si avand valoarea maxima in punctul x - x . Marimea indica probabilitatea ca in urma efectuarii unei masurari sa se obtina o valoare cuprinsa intre x - Ajc si x~ + Ax. Aceasta probabilitate se mai numeste si nivelul statistic de confidenta pentru intervalul de incredere Ax si depinde numai de raportul Ax/a.
Tabelul 1.9. Dependenta probabilitatii P de raportul Ax I a
|
Ax/a |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
Rezulta ca din setul de masurari (1.15) un procent de 68,3% sunt cuprinse intre x -a si x~ + a. Daca, de exemplu, dorim sa avem un nivel statistic de confidenta P = 0,95, este necesar sa luam Ax > 1,96a. Metodele experimentale actuale permit efectuarea unor masurari afectate de erori absolute si relative practic neglijabile. De exemplu, valoarea vitezei luminii in vid este c = (299794245,6 1,1) m/s, ceea ce indica o eroare relativa 8c~3-10~9. Utilizarea ceasurilor atomice cu Cs-133 permite masurarea intervalelor temporale cu o eroare relativa 8t < IO''4, adica cu o eroare de 1 s in decursul a 3-IO6 a. in cadrul sistemului solar, distantele se masoara - in parte - cu ajutorul radarului cu laseri, inzestrate cu ceasuri atomice. Cu aceste mijloace de masurare s-a stabilit distanta medie Pamant - Luna (384420 km) cu o eroare absoluta Aci - 15 cm, adica cu o eroare relativa 8d < 4-IO'10 .
Sisteme de coordonate
Pentru indicarea univoca a pozitiei unui punct material P, se fixeaza un sistem de coordonate format din trei axe perpendiculare intre ele, sau sistemul de coordonate cartezian (fig.1.4). in raport cu un asemenea sistem de coordonate, pozitia punctului material P poate fi data prin cele trei coordonate ale sale x, y, z, sau prin indicarea vectorului de pozitie r, denumit si raza vectoare.
![]()
Unde ex, sunt vectorii unitate ai celor trei axe de coordonate, cu modulele I evl, I ev I, I e. I, iar e,. este vectorul unitate care indica directia OP.
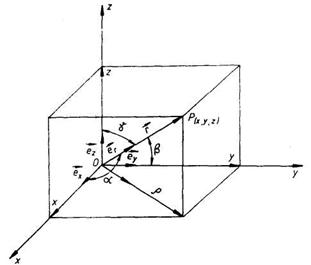 Fig.1.4
Fig.1.4
Directia OP mai poate fi indicata de unghiurile a, P si y pe care aceasta directie le face cu axele Ox, Oy si Oz :
![]()
unde modulul razei vectoare r este
|
|
|
|
Cosinusii directori (1.25) trebuie sa satisfaca conditia:
Rezulta ca numai doua dintre cele trei unghiuri sunt independente. Pentru stabilirea univoca a pozitiei punctului material P sunt necesare doua unghiuri si distanta OP = /'. Directia OP mai poate fi indicata de unghiurile a, P si y pe care aceasta directie le face cu axele Ox, Oy si Oz:
Pozitia punctului material P poate fi stabilita si cu ajutorul unui alt sistem de coordonate, ca de exemplu, sistemul de coordonate sferice (fig l.5). Cunoasterea coordonatelor ;■, 8, cp permite calculul coordonatelor x, y, z :
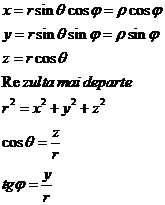
|
|
Este important de retinut ca pozitia univoca a punctului material in spatiu este data fie de un ansamblu de valori (x, y, z), fie de raza vectoare r. Aceasta este o consecinta a faptului ca spatiul in care se desfasoara evenimentele fizice este tridimensional. Se mai spune ca un punct material in spatiu este caracterizat de trei grade de libertate.
Viteza medie se defineste prin raportul dintre vectorul deplasarii si intervalul de timp corespunzator
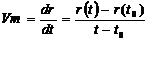
modulul vitezei medii este
![]() iar unitatea de masura este
iar unitatea de masura este ![]()
![]()
Viteza instantanee este limita din viteza medie cand intervalul de timp Δt tinde spre zero:
![]()
![]() unde
unde ![]() este derivata de
ordinul intai a functiei
este derivata de
ordinul intai a functiei ![]() in raport cu timpul,
rezulta ca viteza instantanee v este intotdeauna tangenta la
traiectoriein punctul corespunzator pozitiei punctului material la
momentul respectiv. Putem scrie:
in raport cu timpul,
rezulta ca viteza instantanee v este intotdeauna tangenta la
traiectoriein punctul corespunzator pozitiei punctului material la
momentul respectiv. Putem scrie:
![]()
![]() s-a considerat ca vectori unitate ex si ey nu isi
schimba directiile. Modulul vitezei instantanee este:
s-a considerat ca vectori unitate ex si ey nu isi
schimba directiile. Modulul vitezei instantanee este:
![]()
![]()
Putem scrie vectorul viteza si sub forma:
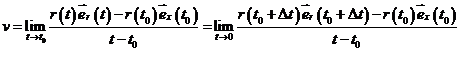
![]()
![]() de unde rezulta mai departe
de unde rezulta mai departe
![]() , dar t este
ales arbitrar, deci
, dar t este
ales arbitrar, deci
![]()
Vectorii ![]() sunt perpendiculari intre ei. Se stie:
sunt perpendiculari intre ei. Se stie:
![]()
![]()
Rezulta mai departe ca produsul scalar dintre un vector unitate si derivata acestuia in raport cu timpul este egal cu zero, ceea ce reprezinta o dovada a faptului ca vectorii respectivi sunt orientati pe directii perpendiculare intre ele.
Acceleratia medie
In intervalul de timp Δt= t - t0, variatia Δv a vitezei este:
![]()
Acceleratia medie se defineste ca fiind raportul dintre variatia vectorului viteza si intervalul de timp corespunzator:
![]()
Acceleratia instantanee este limita din acceleratia medie cand intervalul de timp Δt= t- t0 tinde spre zero, rezulta:
![]()
Acceleratia instantanee este derivata de ordinul intai a
functiei ![]() respectiv derivata de
ordinul al doilea a functiei
respectiv derivata de
ordinul al doilea a functiei ![]() in raport cu timpul. Se mai poate scrie:
in raport cu timpul. Se mai poate scrie:
![]()
![]()
![]()
![]()
![]()
![]() unitatea de masura pentr vectorul
unitate este m/s2. Mai departe tinand seama de
unitatea de masura pentr vectorul
unitate este m/s2. Mai departe tinand seama de ![]() putem scrie:
putem scrie:
![]() adica acceleratia punctului material,
la un moment t, este datorata atat variatiei modulului vitezei cat si
variatiei directiei vitezei v.
adica acceleratia punctului material,
la un moment t, este datorata atat variatiei modulului vitezei cat si
variatiei directiei vitezei v.
MISCAREA RECTILINIE UNIFORMA NORMALA
Daca punctul material se deplaseaza in lungul axei Ox
![]()
![]()
![]()
![]()
sau ![]()
![]()
![]()
![]()
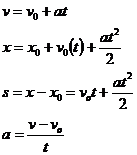 , unde vm este viteza medie
, unde vm este viteza medie
![]()
![]()
![]()
![]() Formula lui Galilei
Formula lui Galilei
MISCAREA CORPULUI RIGID
1) Miscarea de translatie: acel tip de miscare a corpului rigid in care o dreapta legata de corp ramane tot timpul paralela cu pozitia ei initiala (poate fi descrisa ca miscare o dependenta de timp a razei vectoare R(t) si pozitia ei initiala pentru r punct al corpului )
2) Miscarea de rotatie in jurul unei axe fixe, miscare in toate punctele corpului se deplaseaza pe cercuri cu centrele pe dreapta numita axa de rotatie.
![]()
![]()
![]() unde
unde ![]() distanta la axa de rotatie
distanta la axa de rotatie
![]()
![]()
![]()
Miscarea plana: tipul de deplasare a corpului rigid in care toate punctele acestuia se afla intr-un moment in plane paralele
![]()
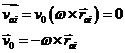
MISCAREA ABSOLUTA, RELATIVA SI DE TRANSPORT
In capitolele precedente s-a aratat ca vitezele si acceleratile unui punct material depind de sistemul de referinta in raport cu care se studiaza miscarea considerata, adica sunt relative. Miscarea punctului material fata de un sistem de referinta K considerat in repaus se numeste miscare absoluta. Miscarea punctului material in raport cu un sistem de referinta K', care se deplaseaza fata de sistemul de referinta K se numeste miscare relativa, iar deplasarea sist de referinta K' fata de K se numeste miscare de transport.
![]()
![]()
![]()
![]() deci viteza absoluta v este suma vectoriala dintre
viteza de transport v0 si viteza relativa v'.
deci viteza absoluta v este suma vectoriala dintre
viteza de transport v0 si viteza relativa v'.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Timand cont de faptul ca:
![]()
Atunci:
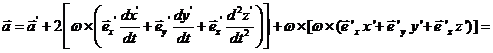
![]()
Daca sistemul de referinta K' efectueaza si o miscare de translatie in raport cu K, putem scrie ca:
![]()
Acceleratia
de transport este suma vectoriala dintre acceleratia a0, datorita
miscarii de translatie, si acceleratia centripeta
![]() datorita miscarii de
rotatie:
datorita miscarii de
rotatie:
![]()
Marimea
![]() Acceleratie Coriolis
Acceleratie Coriolis
![]()
Acceleratia punctului material in raport cu un observator aflat in repaus este data de suma vectoriala dintre acceleratia centripeta si acceleratia Coriolis.
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6529
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved