| CATEGORII DOCUMENTE | ||
|
||
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Rezolvarea numerica a ecuatiilor neliniare
Tematica lucrarii: 1. Generalitati;
2. Metoda bipartitiei;
3. Metoda coardei;
4. Metoda tangentei;
5. Probleme de rezolvat;
6. Concluzii.
1. Generalitati
Ecuatiile reprezinta expresii matematice care contin o variabila (necunoscuta) si pot fi puse sub forma generala:
f(x) = 0 (1)
Egalitatea este valabila numai pentru o multime finita si discreta de valori ale lui x. Expresia f(x) poate contine valori numerice operatori aritmetici si functii elementare. Rezolvarea analitica (pe baza de formule) este posibila numai in anumite cazuri particulare sau pentru ecuatii polinomiale de grad inferior. Rezolvarea numerica permite rezolvarea tuturor tipuri de ecuatii cu aproximatii oricat de bune. Fenomenul de aproximare nu este un impediment deoarece, in final solutia va fi exprimata cu un numar finit de cifre semnificative. Deci metodele de rezolvare numerica sunt singurul instrument viabil pentru rezolvarea ecuatiilor. Trebuie insa mentionat ca rezolvarea globala automata (pentru tot intervalul de variatie a variabilei x) este posibila numai pentru ecuatii polinomiale. Pentru celelalte tipuri de ecuatii (de tip transcendent) aplicarea corecta a metodelor numerice este posibila numai dupa ce au fost identificate intervalele care contin valorile solutiei. In plus utilizarea metodelor numerice locale trebuie precedata de verificarea conditiilor in care acestea pot fi aplicate. Acestea de obicei se refera la proprietatile functiei f(x) (de exemplu continuitatea) sau la cele ale derivatelor functiei.
2. Metoda bipartitiei
Metoda bipartitiei sau a metoda injumatatirii intervalului este o metoda simpla, putin pretentioasa din punctul de vedere a proprietatilor functiei f(x). Totusi este necesar insa ca functia sa fie continua. Presupunem ca intervalul [a,b] contine o solutie a ecuatiei. Atunci:
f(a)f(b) < 0 (2)
Procedura imparte in doua intervalul in care se stie ca exista o solutie. Apoi este evaluata functia la capetele subintervalelor obtinute. Deoarece functia este continua, rezulta ca subintervalul pe care se face schimbarea de semn contine solutia cautata. In continuare acest interval este impartit la randul lui in doua parti egale si analiza continua in acelasi fel. Astfel subintervalul care contine solutia este restrans pe parcursul aplicarii metodei atata timp cat numarul de cifre semnificative disponibil permite marirea rezolutiei.
Procesul iterativ este urmatorul:
Se calculeaza mijlocul intervalului x = (a + b)/2 ;
Se analizeaza semnul functiei la capatul jumatatilor de interval. Portiunea de interval unde are loc schimbarea de semn contine solutia. Procesul injumatatirii se va aplica in continuare pentru acest subinterval:
Daca f(a)f(x ) < 0 atunci b := x ; Mergi la pasul 1;
Daca f(x )f(b) < 0 atunci a := x ; Mergi la pasul 1.
Limbajul MathCad permite exprimarea acestei proceduri sub forma unei singure ecuatii recursive, exprimata vectorial:
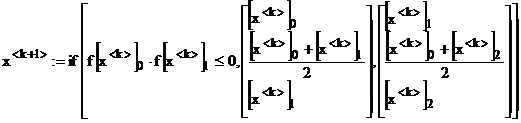 (3)
(3)
In acest cadru memoram in vectorul x capetele si mijlocul intevalului. La fiecare pas vectorului x i se atribuie o noua valoare aleasa diferit, conform algoritmului de mai sus in functie de schimbarea sau conservarea semnului functiei f(x) pe parcursul intervalului. Astfel daca conditia de schimbare a semnului este satisfacuta in jumatatea din stanga a intervalului initial, aceasta va deveni noul interval de lucru. Daca schimbare de semn se produce in jumatatea din dreapta, aceasta va deveni noul interval de lucru.
3. Metoda coardei
Metoda coardei sau a metoda partilor proportionale cere satisfacerea urmatoarelor conditii referitoare la modul de variatie a functiei f(x) pe intervalul unde se aplica metoda. Astfel primele doua derivate ale functiei f(x) sa fie continue pe intervalul (a,b) si sa-si conserve semnul.
Din punct de vedere geometric aceste conditii au urmatoarea interpretare:
* daca prima derivata este continua functia are variatie neteda, fara salturi bruste si fara franturi ale graficului;
* daca prima derivata isi conserva semnul variatia functiei este monotona;
* daca derivata a doua isi conserva semnul functia nu contine puncte de inflexiune.
Solutia aproximativa este calculata la intersectia abscisei Ox cu segmentul de dreapta (coarda corespunzatoare portiunii de grafic) care uneste punctele de coordonate (a,f(a)) si (b,f(b)). Dupa determinarea unei aproximatii a solutiei aceasta devine noul capat al intervalului de lucru si procedeul se aplica in continuare pana cand variatiile solutiei aproximative devin nesemnificative.
Solutia aproximativa la pasul urmator se determina in functie de cea de la pasul precedent printr-un proces de translatie cu incrementul h :
xk+ = xk + h (4)
In functie de pozitia relativa a coardei fata de grafic putem avea doua situatii.
Daca coarda se afla la stanga graficului atunci punctul de pornire al aproximatiilor este punctul a, punctul b ramanand punct fix pe parcursul procesului iterativ, iar deplasarea aproximatiilor se face de la stanga la dreapta. Deci valoarea h este pozitiva, iar valoarea aproximatiei initiale se va considera x = a. Solutia aproximativa xk+1 la pasul k+1 se determina in functie de cea de la pasul precedent xk conform relatiei:
![]() (5)
(5)
Daca coarda se afla la dreapta graficului atunci punctul de pornire al aproximatiilor este punctul b, punctul a ramanand punct fix pe parcursul procesului iterativ, iar deplasarea aproximatiilor se face de la dreapta la stanga. Deci valoarea h este negativa, iar valoarea aproximatiei initiale se va considera x = b. Solutia aproximativa xk+1 la pasul k+1 se determina in functie de cea de la pasul precedent xk conform relatiei:
![]() (6)
(6)
Incadrarea intr-unul dintre cele doua cazuri se face in functie de semnele derivatelor de ordinul unu si doi. Alegerea punctului de pornire al iteratiilor si implicit alegerea relatiei de calcul corespunde valorii pozitive a produsului dintre valoarea functiei si valoarea derivatei a doua in punctul respectiv. Astfel daca f(a)f'(a) > 0, rezulta ca a este punct de pornire si coarda se gaseste la stanga graficului, iar daca f(b)f'(b) > 0, rezulta ca b este punct de pornire si coarda se gaseste la dreapta graficului.
 Fig.1. Interpretarea geometrica a metodei coardei
Fig.1. Interpretarea geometrica a metodei coardei
4. Metoda tangentei
Metoda tangentei sau metoda
lui
f(xk+1 f(xk) + hf'(xk (7)
unde f'(xk) este derivata functiei f(x) in punctul xk ,iar h este distanta dintre punctele xk+1 si xk , h = xk+1 - xk . Din conditia de mai sus se poate evalua h :
![]() (8)
(8)
Metoda tangentei aproximeaxa solutia la pasul k+1 in functie de cea de la pasul k utilizand translatia cu incrementul h.
xk+ = xk + h (9)
Rezulta relatia recursiva pentru aproximatia solutiei la pasul k+1:
![]() (10)
(10)
Pentru ca procesul iterativ sa fie convergent catre solutie este necesar ca punctul de pornire x
sa se conformeze conditiei:
f(x )f''(x ) > 0 (11)
adica functia f(x) si derivata ei de ordinul doi f'(x) sa aiba acelasi semn.
 Fig.2.
Interpretarea geometrica
Fig.2.
Interpretarea geometrica
a metodei tangentei
5. Probleme de rezolvat
Rezolvarea unei ecuatii de gradul II
Se considera ca exemplu ecuatia de gradul doi, de forma:
x2 - 4x +1 = 0 (12)
Aceasta ecuatie poate fi pusa sub forma :
f(x) = 0 unde f(x) = x - 4x +1 (13)
Se poate observa (prin trasarea graficului, de exemplu) ca ecuatia are doua solutii in intervalele (0 ) si (2,4).
Pentru a aplica metodele numerice de rezolvare, definim (in MathCad) functia f(t) cu variabila generica t:
![]() (14)
(14)
Aceasta functie reprezinta o parabola de gradul doi si poate fi reprezentata grafic in MathCad (fig.1). Pentru aceasta se utilizeaza pentru variatia argumentului diviziunea de puncte ti :
![]() (15)
(15)
unde: i := 1..M este o variabila sir, M este numarul total de puncte, iar h este pasul de variatie. Marimea pasului h determina rezolutia (finetea de variatie) graficului. Numarul M determina numarul de pasi. Acesta corelat cu marimea pasului determina intervalul total de variatie.
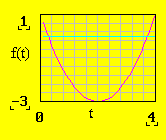 Fig.1
Varatia functiei f(t) pe intervalul [0,4]
Fig.1
Varatia functiei f(t) pe intervalul [0,4]
Rezolvarea ecuatiei date, in multimea numerelor reale, este echivalenta cu cautarea punctelor de anulare a functiei f(x).
Pentru a putea aplica metodele de aproximare iterativa a solutiei, definim numarul maxim de iteratii N si variabila sir k := 1..N .
a) Aplicarea metodei bipartitiei (injumatatirii intervalului) in cadrul interpretorului de expresii matematice MathCad impune transformarea algoritmului intr-o singura ecuatie recursiva. Deoarece algoritmul lucreaza in acelasi timp cu coordonatele capetelor si mijlocului de interval, trebuie sa utilizam forma vectoriala. Astfel sirul de vectori v<k> va reprezenta, pentru fiecare k, coordonatele capetelor si mijlocului de subinterval care contine una dintre radacini. Pe masura ce procesul iterativ avanseaza marimea subintervalului care contine solutia se micsoreaza, obtinand pentru aceasta o aproximatie din ce in ce mai buna.
Ecuatia vectoriala recursiva, utilizata pentru aproximarea unei radacini, este:
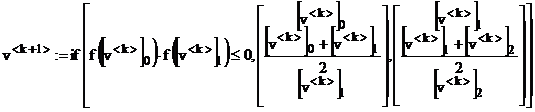 (16)
(16)
Aceasta ecuatie trebuie aplicata pentru fiecare interval care contine o radacina a ecuatiei. Pentru prima radacina se poate alege intervalul [0 ], pentru care rezulta urmatoarele valori pentru coordonatele vectorului de pornire v<0> si vectorului obtinut dupa N iteratii v<N>
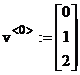
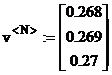 (17)
(17)
Pentru cea de-a doua radacina se poate alege intervalul [2,4], pentru care rezulta urmatoarele valori pentru coordonatele vectorului de pornire v<0> si vectorului obtinut dupa N iteratii v<N>
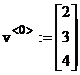
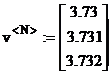 (18)
(18)
b) Pentru a aplica metoda lui partilor proportionale (metoda coardei) pe intervalul [a,b] = [0,4] se utilizeaza sirurile de aproximare definite prin urmatoarele ecuatii recursive:
![]() (19)
(19)
in cazul cand se considera a := 0 punct fix si x := 0.5 valoare initiala;
![]() (20)
(20)
in cazul cand se considera b := 4 punct fix si x := 3.5 valoare initiala.
c)
Pentru a aplica metoda
lui
![]() (21)
(21)
unde functia g(t), egala cu derivata (analitica) a functiei f(t):
![]() (22)
(22)
Pentru a obtine cele doua solutii ale ecuatiei de gradul doi, avand in vedere ca metoda de aproximare este eficace numai atunci cand este aplicata in intervalul care contine o singura radacina, se vor utiliza valori diferite pentru aproximatiile initiale. Astfel in urma procesului iterativ se obtin, pentru fiecare caz, urmatoarele rezultate:
- pentru valoarea initiala: x rezulta: xN (23)
- pentru valoarea initiala: x rezulta: xN (24)
Observatii:
Estimarea solutiei exacte se poate face fie cu ajutorul graficului funtiei asociate ecuatiei, fie utilizand instructiunea 'root' a limbajului MathCad;
La metoda bipartitiei precizia solutiei este data de distanta dintre capetele subintervalului obtinut dupa N iteratii;
Metodele tangentei si coardei au de regula o viteza de convergenta mai ridicata, dar impun restrictii asupra modului de variatie a functiei.
Se cere:
Implementarea algoritmilor de rezolvare in limbaj MathCad;
Stabilirea numarului de iteratii pana la stabilizarea solutiei aproximative;
Analiza rezultatelor si vitezei de convergenta pentru metodele prezentate mai sus;
Comparatia cu solutia calculata iterativ, utilizand rezolvitorul disponibil in cadrul programului MathCad.
6. Concluzii
Metodele numerice prezentate au un caracter local (sunt aplicate in intervalul in care exista o singura radacina).
Metoda bipartitiei poate fi aplicata in conditii mai putin restrictive pentru functia f(x).
Metodele coardei si tangentei pot fi aplicate combinat pentru izolarea bilaterala a solutiei.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5254
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved