| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
4. Operatii cu vectori alunecatori
Solid rigid = corp solid nedeformabil . Oricat de mari ar fi fortele care actioneaza asupra lui, doua puncte de pe suprafata sa raman la aceeasi distanta, (fig. 4.1) .
|
|
Fortele care actioneaza asupra solidului rigid sunt
vectori alunecatori .
Vector alunecator - vector care aluneca pe dreapta sa suport . Fig. 4.1
|
|
![]() 5 elemente scalare (fig. 4.2)
5 elemente scalare (fig. 4.2)
O multime de vectori alunecatori constituie un sistem de vectori alunecatori .
Fig. 4.2
4.1. Momentul unui vector alunecator in raport cu un punct
|
|
![]()
Se defineste ca moment al vectorului alunecator v in raport cu punctul O, (fig.
4.3) vectorul legat cu originea in O, a carui expresie este:
Proprietati : ![]() = vector
= vector
- pe planul determinat de v si o
- sensul dat de sensul de insurubare al
burghiului drept
Fig. 4.3
- modul:
![]() (2)
(2)
unde : d - distanta de la punctul O la
suportul ( D
) al vectorului ![]() d D
d D
![]()
Daca notam :
![]()
- Daca ![]() aluneca pe suport momentul vectorului nu se
modifica ( fig. 4.4 )
aluneca pe suport momentul vectorului nu se
modifica ( fig. 4.4 )
|
|
Demonstratie :
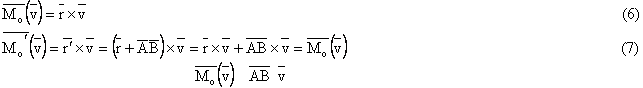
Fig. 4.4
- ![]() vectorial raportat la un sistem de axe xOyz
vectorial raportat la un sistem de axe xOyz

- Deoarece ![]()
![]() Þ
Þ ![]()
![]() = o (produsul scalar a doi vectori perpendiculari este egal cu zero)
= o (produsul scalar a doi vectori perpendiculari este egal cu zero)
4 2. Momentul unui vector alunecator in raport cu o axa
Prin definitie, momentul unui vector alunecator in raport cu o axa este proiectia pe axa a momentului vectorului in raport cu un punct oarecare de pe axa (fig. 4.5).
![]() (10)
(10)
|
|
Observatie: MΔ este scalar.
![]() (11) (11)
(11) (11)
Proprietati:
- MD = 0 daca vectorul este paralel cu axa sau intersecteaza axa
- M D nu se modifica daca vectorul aluneca pe suportul sau
[demonstrat ca la ![]() ]
]
Fig. 4.5
5. Sisteme de vectori alunecatori
5.1. Operatii elementare de echivalenta pentru vectori alunecatori
Operatii elementare de echivalenta - sunt acele operatii simple care se pot face cu vectorii alunecatori ai unui sistem astfel incat sistemul rezultat sa fie echivalent cu cel initial (aceste operatii sa nu modifice actiunea mecanica a vectorilor) .
In principal acestea sunt :
alunecarea unui vector pe suportul sau;
inlocuirea vectorilor concurenti cu rezultanta lor;
adaugarea sau suprimarea a doi vectori egali in modul, de sens opus, avand acelasi suport;
compunerea sau descompunerea unui vector dupa doua directii in plan sau trei directii in spatiu .
Fiind dat un sistem de patru vectori alunecatori (fig. 5.1), acestia se pot echivala (se pot reduce, substitui) in raport cu un punct O oarecare al sistemului dat la un sistem de doi vectori : R si Mo
|
|
unde :
![]()

![]() - rezultanta
(vector rezultant)
- rezultanta
(vector rezultant)
![]() - vector moment
rezultant
- vector moment
rezultant
![]() si
si ![]() inlocuiesc sistemul dat de patru vectori si
alcatuiesc torsorul de reducere in punctul O al sistemului de vectori
alunecatori dati . Fig.
5.1
inlocuiesc sistemul dat de patru vectori si
alcatuiesc torsorul de reducere in punctul O al sistemului de vectori
alunecatori dati . Fig.
5.1
![]() ,
, ![]() - torsorul de reducere
- torsorul de reducere
Observatie!!! Componentele ![]() si
si ![]() ale torsorului de reducere ale unui
sistem de vectori alunecatori
ale torsorului de reducere ale unui
sistem de vectori alunecatori
intr-un punct O sunt invariante fata de operatiile elementare de echivalenta .
Proprietatile vectorului moment rezultant ![]()
|
|
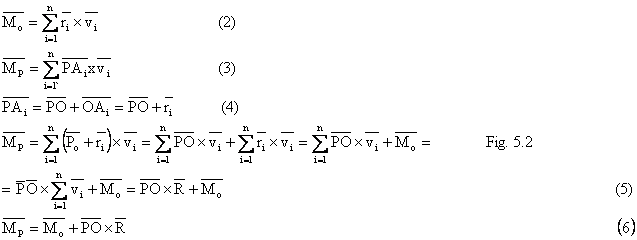
- variatia vectorului moment rezultant fata de
punctul de reducere O, (fig. 5.2)

- trinom invariant
- momentul unui cuplu de vectori
|
|
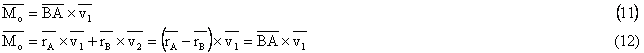
Cuplu de vectori - ansamblu de doi vectori paraleli, egali in modul, de
sensuri contrare pe suporturi diferite, (fig. 5.3) .
Proprietati
![]() ,
(fig. 5.4) :
,
(fig. 5.4) :
vector liber
directie pe planul format de cei 2 vectori
sensul de insurubare al burghiului drept Fig. 5.3
modul: ½![]() ½=½
½=½![]() ½ d
½ d
unde: d - distanta dintre cei 2 vectori pe suport
|
|
|
|
Fig. 5.4
5.3. Axa centrala a unui sistem de vectori alunecatori
Axa centrala este locul geometric al punctelor pentru care vectorul rezultant si vectorul moment rezultant sunt coliniari si este o dreapta pe care vectorul moment rezultant este minim .
|
|
Date
O, ![]() si
si ![]()
Se cer ecuatiile axei centrale.
Se considera un sistem xOyz si torsorul de reducere se afla in O, (fig. 5.5) .
Proiectand
![]() si
si ![]() pe cele 3 directii avem:
pe cele 3 directii avem:
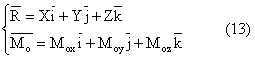
Fig. 5.5
Presupunem
ca ![]() face unghiul a cu
face unghiul a cu ![]() . Daca a = 0 sau a = p rezulta
. Daca a = 0 sau a = p rezulta ![]() si
si ![]() sunt coliniari . In acest caz torsorul se
numeste torsor minimal .
sunt coliniari . In acest caz torsorul se
numeste torsor minimal .
![]()
Pentru a determina locul geometric presupunem ca exista un punct C astfel
incat:
l - scalar arbitrar

Conform (6) :
![]()
Inlocuind (16) in (15) =>
![]()
Tinand cont de (13) obtinem urmatoarele relatii scalare :
![]()
Relatiile (18) permit determinarea ecuatiilor axei centrale sub forma analitica :
![]()
Relatia (19) reprezinta ecuatiile axei centrale care sunt intersectia a doua plane.
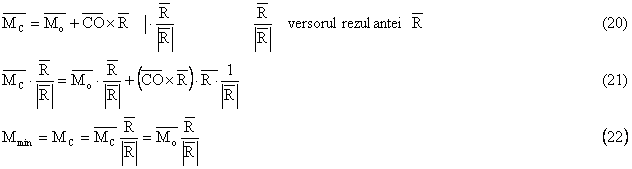
In relatia (19) x, y, z sunt coordonatele unui punct curent al axei centrale.
Momentul rezultant care se obtine prin reducerea sistemului de vectori dati in raport cu un punct al axei centrale se numeste moment minim .
Scalar relatia (22) devine :
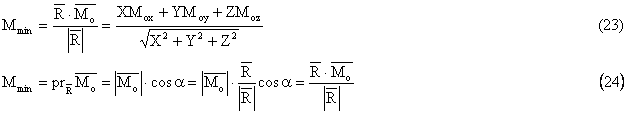
5.4 Cazuri de reducere a sistemelor de vectori alunecatori
Date: O ![]()
![]()
Cazuri de reducere:
- ![]() = 0 ;
= 0 ; ![]() = 0
sistem echivalent cu zero (solidul este in echilibru)
= 0
sistem echivalent cu zero (solidul este in echilibru)
![]() ¹ 0 ;
¹ 0 ; ![]() = 0 sistem echivalent cu o
forta unica
= 0 sistem echivalent cu o
forta unica ![]() (rezultanta) aplicata in punctul de reducere O
avand directia axei centrale .
(rezultanta) aplicata in punctul de reducere O
avand directia axei centrale .
- ![]() = 0 ;
= 0 ; ![]() ¹ 0 sistem echivalent cu un cuplu de moment
¹ 0 sistem echivalent cu un cuplu de moment ![]() (fig. 5.6)
(fig. 5.6)
|
|
Fig. 5.6
- ![]() ¹ 0 ;
¹ 0 ; ![]() ¹0 :
¹0 :
a)
![]()
![]() =
0 (
=
0 (![]()
![]() ) - sistem echivalent cu o forta unica
rezultanta avand directia axei centrale si aflandu-se la distanta d = Mo/R
de punctul de reducere (fig. 5.7) .
) - sistem echivalent cu o forta unica
rezultanta avand directia axei centrale si aflandu-se la distanta d = Mo/R
de punctul de reducere (fig. 5.7) .
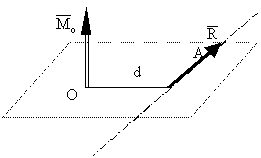
Fig. 5.7
b)
![]()
![]() ¹
0 - sistem echivalent cu un torsor minimal pe axa centrala (fig. 5.8).
¹
0 - sistem echivalent cu un torsor minimal pe axa centrala (fig. 5.8).

Fig. 5.8
![]() -
directia axei centrale
-
directia axei centrale
![]() -
momentul unui cuplu care actioneaza intr-un plan pe axa centrala .
-
momentul unui cuplu care actioneaza intr-un plan pe axa centrala .
|
|
Aplicatie
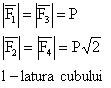 |
Se cer :
1) torsorul in O
2) torsorul in B
3) cu ce este echivalent
sistemul
4) axa centrala si elementele
de reducere pe axa centrala![]()
si Mmin
Fig. 5.9
Se intocmeste urmatorul tabel :
|
Fi |
Xi |
Yi |
Zi |
Mix |
Miy |
Miz |
|
|
F1 |
0 |
0 |
P |
0 |
0 |
0 |
|
|
F2 |
F2` |
P |
0 |
0 |
0 |
0 |
-Pl |
|
F2 ` |
0 |
0 |
P |
Pl |
0 |
0 |
|
|
F3 |
0 |
0 |
P |
Pl |
-Pl |
0 |
|
|
F4 |
F4 |
-P |
0 |
0 |
0 |
0 |
0 |
|
F4 |
0 |
0 |
P |
0 |
-Pl |
0 |
|
|
∑ |
0 |
0 |
4P |
2Pl |
-2Pl |
-Pl |
|
![]()
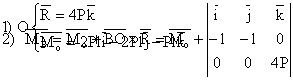
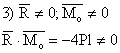
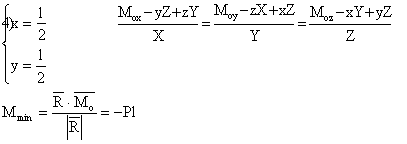
Conform pct. 3 sistemul este echivalent cu un torsor minimal pe axa centrala
Sisteme particulare de vectori alunecatori

Sisteme de vectori alunecatori concurenti
Se considera un sistem de vectori alunecatori concurenti (fig. 5.10):
|
|
torsorul de reducere

Fig. 5.10
Cazuri de reducere :
![]() = 0 - sistem echivalent cu zero
= 0 - sistem echivalent cu zero
![]() ¹ 0 - sistem
echivalent cu o forta unica rezultanta
¹ 0 - sistem
echivalent cu o forta unica rezultanta
Sisteme de vectori alunecatori coplanari
|
|

Fig. 5. 11
Cazuri de reducere :
![]() = 0 ,
= 0 , ![]() = 0 - sistem echivalent cu zero
= 0 - sistem echivalent cu zero
![]() = 0 ,
= 0 , ![]() ¹ 0 - sistem echivalent cu un cuplu de moment M
¹ 0 - sistem echivalent cu un cuplu de moment M
![]() ¹ 0 ,
¹ 0 , ![]() = 0 - sistem echivalent cu o forta unica
rezultanta pe axa centrala care trece
= 0 - sistem echivalent cu o forta unica
rezultanta pe axa centrala care trece
|
Fig. 5.12 |
prin O (fig. 5.12)
![]() ¹ 0 ,
¹ 0 , ![]() ¹0 - axa centrala nu trece prin O
¹0 - axa centrala nu trece prin O
![]()
Ecuatiile axei centrale :

unde α este unghiul facut de R cu X
Sisteme de cupluri
|
|

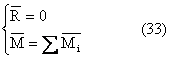
caz general (fig. 5.13)
torsorul de reducere
Cazuri de reducere :
-![]() = 0 - sistem echivalent cu zero
= 0 - sistem echivalent cu zero
-![]() ≠
0 - sistem echivalent cu un cuplu de moment M
≠
0 - sistem echivalent cu un cuplu de moment M
Sisteme de vectori alunecatori paraleli
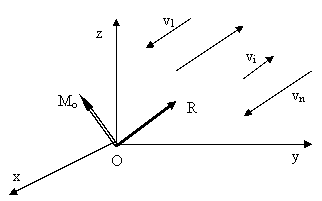

Consideram ![]() - versorul directiei vectorului
- versorul directiei vectorului ![]()
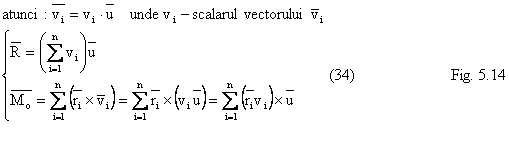
(fig. 5.14).
![]() ║
║ ![]() (35)
(35)
![]() ┴
┴
![]() =>
=> ![]() ┴
┴ ![]() =>
=> ![]() ∙
∙![]() = 0 (36)
= 0 (36)
Cazuri de reducere :
![]() = 0 ,
= 0 , ![]() = 0 - sistem echivalent cu zero
= 0 - sistem echivalent cu zero
![]() = 0 ,
= 0 , ![]() ¹ 0 - sistem echivalent cu un cuplu de moment
¹ 0 - sistem echivalent cu un cuplu de moment ![]()
![]() ¹ 0 ,
¹ 0 , ![]() ≠ 0 - deoarece avem
≠ 0 - deoarece avem ![]()
![]() = 0 - sistem echivalent cu un vector unic rezultanta
pe axa centrala
= 0 - sistem echivalent cu un vector unic rezultanta
pe axa centrala
- ![]() ¹ 0
¹ 0 ![]() = 0 - axa centrala trece prin O
= 0 - axa centrala trece prin O
![]() ≠ 0 - axa centrala nu trece prin O
≠ 0 - axa centrala nu trece prin O
Axa centrala pentru vectori paraleli
|
|
Fie P un punct al axei centrale (fig. 5.15) .
Deoarece ![]() ∙
∙ ![]() = 0 => Mmin = 0
= 0 => Mmin = 0

Inlocuind (40) si (41) in (39) => Fig. 5.15
![]()
![]()
λ - scalar arbitrar

![]() -
vector de pozitie curent al axei centrale
-
vector de pozitie curent al axei centrale

Notam :
vectorul de pozitie al unui punct C al axei centrale numit si centrul vectorilor paraleli
Introducem parametrul :

Relatia (48) reprezinta ecuatia vectoriala a axei centrale
Proprietati ale axei centrale :
este paralela cu versorul ![]() al vectorilor paraleli;
al vectorilor paraleli;
trece prin punctul C - centrul vectorilor paraleli.
Proprietati ale centrului vectorilor paraleli C :
pozitia lui C este independenta de directia vectorilor;
pozitia lui C nu se modifica daca toti vectorii sistemului se amplifica cu acelasi scalar;
pozitia lui C este independenta de originea sistemului de axe ales ;
coordonatele lui C in raport cu sistemul de axe ales sunt :



|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2009
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved