LOGICA - Logica clasica, Logica matematica

LOGICA

ogica este stiinta al carui obiect este stabilirea conditiilor corectitudini gandirii, a formelor si legilor generale ale rationarii juste, conforme prin ordinea ideilor cu organizarea legica a relatiilor obiective. In stabilirea acestor conditii, logica face abstractie de continutul concret al diverselor noastre idei, fiind in acest sens o stiinta formala, analoaga cu gramatica sau cu geometria. Asa, de pilda, ea se ocupa cu notiunea sau cu judecata in genere si cu o anumita notiune sau judecata determinata concret. Logica se imparte in trei ramuri mari: a) logica clasica (formal filozofica), b) logica matematica (simbolica, numita si logistica) si c) logica dialectica. Logica clasica si logica matematica expun formele si legile gandiri concrete in momentul relativei lor stabilitati, in timp ce logica dialectica le expune in procesul miscarii si dezvoltarii, al dialecticii lor. De aceea logica clasica si logica matematica sunt subordonate, prin natura lor, logici dialectice, pe baza faptului ca stabilitatea, in genere, este relativa fata de caracterul absolut al miscarii si, ca atare, prin natura ei, subordonata acesteia.

Logica clasica (logica de traditie aristotelica) studiaza notiunea, judecata, ca raport intre notiuni, si rationamentul, ca raport intre judecati. Ceea ce caracterizeaza logica clasica este relevarea raportului de determinare de la general la particular, de la gen la specie, generalul si esentialul fiind considerate fundamentele pentru o cunoastere stiintifica veritabila. Aceste cerinte sunt intruchipate de silogism, pe baza functiei indeplinite in cadrul sau de termenul mediu. Intemeiatorul logici clasice a fost Aristotel, descoperitorul silogismului si al doctrinei despre silogism, silogistica. Preocupari de sistematizare a logici au existat, de asemenea, in China si in India antica. Contributii uluitoare la dezvoltarea logicii clasice au adus stoicii, precum si logicienii evului mediu. In stransa legatura cu dezvoltarea moderna a stiintei s-a dezvoltat teoria inductiei si s-au formulat regulile rationamentului inductiv. Prin fundamentarea consecvent materialista a conceptului de adevar, pe baza stabilirii raportului just dintre logic, gnoseologic si ontologic, logica clasica continua sa se dezvolte si in prezent, impotriva tendintelor neopozitiviste de a-i nega valabilitatea.

Logica matematica (sau simbolica) s-a nascut in sec. al XIX-lea, in functie de dezvoltarea puternica a matematici si de ivirea necesitatii cercetarii logice a fundamentului acesteia ca stiinta formala. Atat prin originea cat si prin problematica sa, logica matematica este o stiinta care a aparut la hotarul dintre logica si matematica. Logica matematica se caracterizeaza prin cercetarea functorilor (operatorilor) logici, a proprietatilor lor formale si prin elaborarea, pe aceasta baza, a unor calcule logice. Procedeul logic-matematic, pastrandu-si specificul sau, este pe deplin analog procedeului matematic propriu-zis. In virtutea acestui procedeu, cercetarile de ordin logic au o formalitate riguroasa, datorita careia operatia de deductie isi desavarseste stringenta. Astfel se elaboreaza o serie de calcule care imbratiseaza aspecte noi, necercetate inca in domeniul logicii. Calculele cele mai insemnate si care reprezinta totodata capitole de baza ale logici matematice sunt: a) logica propozitiilor, b) logica predicatelor, c)logica relatiilor. In cadrul logici matematice au aparut sau au luat o noua dezvoltare logica modala, logica polivalenta, precum si logica inductiva, strans legata de teoria probabilitatilor. Analiza fundamentelor logici a determinat aparitia cercetarilor de logica combinatorie. Tot atat de importante ca si problemele stricte de calcul (probleme sintactice) sunt si problemele interpretarii acestor calcule (probleme de semantica); in aceasta privinta trebuie mentionata mai ales problema analizei sistemelor formale insesi in cercetarile de metalogica. O data cu problemele de metalogica trec pe prim plan analize cu implicatii gnoseologice in legatura cu adevarul si cu consecventa in limbajul formalizat. Cercetarile de logica matematica au infirmat intrebuintarea formalist-metafizica a sistemelor formale si cea conventionalist-relativista a conceptului de adevar, proprie neopozitivismului. Ideea calculului logic a fost formulata pentru prima oara de Leibniz. Ca disciplina de sine statatoare, logica matematica s-a constituit in sec. al XIX-lea, o data cu aparitia oprelor lui A. de Morgan si ale lui G. Boole, care au inaugurat asa-numita algebra a logici, dezvoltata ulterior de E. Schroder, P. S. Poretki s. a. Logica matematica gaseste aplicare in electrotehnica (studiul schemelor cu relee, al schemelor electronice etc. ) in cibernetica (teoria automatelor, tehnica programarii), in neurofiziologie (modelarea sistemelor neurotice), lingvistica (lingvistica matematica) etc.

Logica dialectica este teoria de ordin logic a materialismului dialectic, adica analiza dialecticii formelor logice si a legilor care conditioneaza aceasta dialectica; pe baza lor gandirea reflecta in mod adecvat miscarea si dezvoltarea realitatii obiective. Acest lucru este demonstrat riguros de dezvoltarea dialectica a notiuni, care trece in judecata, si a judecatii care trece in silogism. Formele logice sunt, datorita valorii lor gnoseologice diferentiate, forme pline de continut, iar legile logice pe baza carora acestea se inlantuiesc, constuitue principiul de baza al logicii dialectice. In aceasta lumina trebie inteleasa si relevarea unor trasaturi generale ale logici dialectice, cum sunt, de ex. Identitatea concreta, care cuprinde in sine deosebirea; predictia complexa contradictorie, care reprezinta un mod de expromare pe plan logic a contradictiei interne; inmladirea tertului exclus, care reprezinta supletea conceptului de adevar in aprofundarea cunoasterii. In acest fel logica dialectica elimina posibilitatea strecurari unei sciziuni in analiza si sinteza, in general si particular, intre inductie si deductie, intre abstract si concret, sciziune prin care idealismul, in special pozitiv logic, incearca sa se infiltreze inlauntrul logici pentru ai denatura si vicia caracterul stiintific. Interpretarea de catre logica dialectica a formei de manifestare a continutului demonstreaza legatura si unitatea fundamentala dintre logica si teoria cunoasterii. Studierea, pe baza practicii social-istorice, a procesului de constituire si dezvoltare a formelor logice demonstreaza ca axiomele insesi sunt rezultatul precticii de miliarde de ori repetate. Dialectica formelor logice isi gaseste explicare stiintifica in istoria cunoasterii. Logicul este un rezumat al istoricului, iar unitatea lor este baza explicarii materialist-dialectice a insasi esentei formatiilor logice: cunoasterea, in dezvoltarea ei, realizeaza coinciderea dialectica a logicului cu ontologicul scotand in evidenta caracterul concret al adevarului si corelatia dialectica dintre adevarul relativsi cel abolut. Logicul si gnoseologicul coincid astfel cu ontologicul. Unitatea dintre logica, teoria cunoasterii si dialectica este concluzia logici dialectice si, ca atare, a logici in genere ca stiinta a corectitudini gandirii si totadata a adevarului ei, formele logice redand, prin dialectica lor, continutul realitatii obiective in dezvoltarea lui. In acest sens, logica dialectica este, in intelesul deplin al cuvantului, filozofia logicii, interpretarea logici ca "organon ", instrument de cuprindere completa, in concepte, a realitatii obiective. Logica dialectica a aparut in expresia ei stiintifica ca parte componenta a filozofiei marxiste, prin interpretarea materialista a dialecticii de catre clasicii marxism-leninismului. Obiectul si legile constituie o preocupare permanenta in lucrarile logicienilor marxisti.

Logica combinatorie, cea mai noua parte a logici matematice, alcatuita dintr-un calcul in care exista numai constante, asa-numitii combinatori; acestia apar si in rol de functori, si in rol de argument. Logica combinatorie isi indreapta, in ultima vreme, cercetarile in deosebi in directia analizei fundamentelor logici.

Logica constructivista, curent in logica matematica, caracterizat prin construirea inductiva a expresilor logice. Ideea de baza a logici constructivista consta in interdictia de a transfera asupra multimilor infinite priincipiile valabile pentru multimile finite (legea dublei negatii, principiul tertului exclus s. a. ). Logica constructivista se deosebeste de logica clasica si prin aceea ca ea considera infinitul ca fiind potential, in curs de construire, pe cand aceasta din urma il percepe ca fiind actual, realizat. Pornind de la principiile logici constructiviste, se fac incercari in directia reconsiderarii fundamentelor logicii matematice moderne si ale matematici. Bazele logici constructiviste au fost puse in scoala intuitionista.

Logica relatiilor, curent logic format la sfarsitul sec. al XIX-lea. Logica realtiilor cerceteaza propietatiile formale ale relatiilor (tranzivitatea, reflexivitatea, simetria etc. ) si efectueaza calculul relatiilor, contribuind la analiza logica a expresiilor matematice. Ea a capatat in filozofia burgheza contemporana o interpretare idealista, potrivit careia relatia este considerata ca fiind primordiala pe plan logic, gnoseologic si ontologic fata de relate (termenii relatiei). Desi natura relatelor se manifesta prin relatie, ea determina totusi natura relatiei (ex. Greutatea unui corp se stabileste in relatie cu alt corp, insa greutatea nu este o propietate a relatiei insasi, ci a corpurilor respective, ea manifestandu-se doar prin aceasta relatie). Interpretata just, logica relatiilor constituie un capitol principal al logici matematice.

Logica modala, sistem logic care analizeaza, din punct de vedere formal, raporturile dintre necesitate, realitate, posibilitate, imposibilitate si contingenta. Prima elaborare a unui sistem logic al modalitatii a fost facuta de Aristotel (silogistica); o noua dezvoltare pe linia logici modale are loc astazi in cadrul logicii matematice (ex. sistemul trivalent si cel tetravalent al lui J. Lukasiewicz sau sistemele axiomatice de implicatie stricta ale lui C. I. Lewis). Pana in prezent logica modala nu a fost elaborata sub toate aspectele.

Logica polivalenta, sistem logic formal ale carui expresii comporta, spre deosebire de logica traditionala, care era bivalenta, mai mult decat doua valori de adevar, ea putand fi astfel trivalenta, tetravalenta sau n-valenta. Primele sisteme de logica polivalenta au fost construite de J. Lukasiewicz (1920) si de E. Post (1921). Sistemele de logica polivalenta prezinta atat interes teoretic cat si practic, legat de interpreterea mecanicii cuantice, de rezolvarea paradoxelor logicii matematice clasice, de teoria schemelor de relee etc.

VIATA LUI ARISTOTEL - inceputurile logicii traditionale

Unul dintre cei mai mari filozofi care au existat, Aristotel, s-a nascut in orasul Stagira din peninsula Chalcis, in anul 384 i. Hr. .

Tatal sau, medicul Nicomah, venise impreuna cu familia sa in Chalcis, din Mesenia, in secolul VIII sau VII i. Hr. . Nicomah nu era doar un simplu medic, ci un om cu carte, care a scris chiar doua lucrari literare.

Evident, viitorul micului Aristotel a fost influentat si de tatal sau, care l-a initiat in arta medicala, fiind, desigur, deosebit de destoinic, de vreme ce a fost medic regal la curtea macedoneana.

Mama sa, Phaetis, era din Stagira, lucru ce a fost demonstrat si prin retragerea lui Aristotel, cand a fost incoltit de dusmanii sai politici, pe o proprietate din Stagira, mostenire materna.

Desi Stagira, orasul natal al lui Aristotel, era pe granita cu regatul mecedonean, el nu a fost ''semigrec'' asa cum au crezut o vreme unii autori.

Aristotel, pleaca din Stagira la varsta de 17 ani, pana atunci fiind sub instruirea tatalui sau si la curtea regala (pana la 15 ani) si sub directa indrumare

a lui Proxenos, dupa pilda parintilor sai.

La 18 ani Aristotel soseste la vestita Academie ateniana unde l-a avut ca profesor pe Platon. Spre surprinderea lui, afla ca acesta a fugit din cetate ca sa scape de supararea tiranului Denys cel Tanar.

Aristotel va fi dezamagit de aceasta veste, care-i amana intalnirea cu gloria filozoficadeatunci, si langacelcareastepta nerabdator sase desavarseasca.

Deocamdata, cum am zis, conducatorul Academiei nu se afla in cetate, dar Aristotel e decis sa-l astepte.

Acesti trei ani, cat ''rectorul'' Academiei isi va consuma iluziile politice

don - quijotesti, incercanddinnousa convinga fara succes conducatorii Syracuzei de valabilitatea ideilor sale desprestatul ideal, ii vor folosi lui Aristotel sa se pregateasca temeinic pentru a se ridica la nivelul teoretic al comunitatii filozofice in care intrase.

Cu banii pe care-i avea a descoperit destul de usor ca negustorii atenieni erau priceputi si in valorificarea manuscriselor filozofice ori stiintifice. Acestea constituiau in acel moment pentru el marfa cea mai de pret pe care o avea Atena, si in achizitionarea ei nu si-a crutat cu nimic avutul.

''Noul'' care insemnase geneza filozofiei in Grecia aparuse pe coastele Asiei - Mici, in Ionia, laintersectiile drumurilor comerciale care legau Orientul de bazinul mediteranean, in cetatile infloritoare cum erau Foceea, Milet, Efes, framantate de miscari sociale care se reflectau, inevitabil, si in diversitatea pozitiile filozofice.

Caracterul materialist al primei filozofii grecesti nu i-a putut scapa lui Aristotel. ''Din ceea ce s-a spus si din doctrinele filozofilor cu care am conferit

, iata deci ceea ce am cules: pe de o parte, cei mai vechi filozofi considera principiul ca fiind corporal (caci apa si focul si elementele analoge sunt corpuri)

la unii acest principiu corporal e unic, la altii el este multiplu, insa si unii, si altii il concep ca fiind de natura materiei''. (Metafizica, Tricot, pag. 27)

Opera scrisa in vremeaaceasta poarta anumite caracteristici si reflecta gradul de pregatire, influentele si straduintele de orientare ale tanarului filozof.

Aristotel scrie cu inflacarare, mai ales dialoguri (precum se vede, invatacelul accepta si imita tehnica de compozitie a maestrului, fara sa-l poata ajunge insa nici in stralucirea artistica a expresiei, nici in adancimea ideilor).

Sa zicem insa ca deocamdata, in Academie, filozoful nostru e inca tanar si pasionat cercetarea teoretica, absorbit mai presus de orice exactitate si adevar, deevidentarationala a intemeierii concluziilor si de oglindirea intocmai a faptelor.

Aristotel se casatoreste cu Pythia, cu carea dus o viata linistita si afectuoasa. Filozoful a avut din aceasta casatorie o copila care purta numele mamei si pe care, cand isi intocmeste testamentul, o destineaza ca sotie lui Nicanor, fiul lui Proxenos, primul sau tutore-educator. Pythia, sotia, a murit, probabil imediat dupa intoarcerea lui Aristotel la Atena, in 335 i. Hr. sau, eventual, in timpul vreunei calatorii in aceasta cetate. Astasededucedin testamentul lui in care stabileste ca osemintele primei sotii sa fie asezate in acelasi mormant cu ale sale, ceea ce poate sa insemne ca ele se aflau undeva in preajma Atenei, deoarece aducerea lor din indepartata Macedonie sau din alta parte nu putea fi usor de indeplinit.

Teoretic, Aristotel s-a indepartat si mai mult de Platon, cautandu-si propriul sau drum filozofic, adancind cercetarile stiintifice si luand pozitie critica si mai accentuata fata de doctrina ideilor.

In calmul acestor preocupari stiintifice, imbinate cu tihna unei familii in care si-a gasit toata multumirea omeneste posibila, caci fericirea adevarata o gusta in contemplarea teoretica, l-a gasit pe Aristotel chemarea regelui Filip al Macedoniei, care dorea sa-l aiba dascal si educator fiului sau Alexandru, atunci in varsta de abia treisprezece ani.

Se deschide astfel o noua perioada, de aproximativ un deceniu, in care evenimentul cel mai de seama, ramas legendar in istorie prin faima celor doi actori principali ai sai, a fost activitatea de instruire si educare a lui Alexandru care in curand avea sa fie ''cel Mare'', unul din cei mai intreprinzatori si temerari razboinici ai istoriei.

Asupra sfarsitului lui Aristotel au existat iarasi felurite versiuni printre autorii vechi. Unii spuneau ca s-ar fi otravit de teama continuarii unui proces, in care, desi el era intemeietorul logicii, nu se putea apara deoarece nici nu era ascultat de catre instanta; altii, ca s-ar fi aruncat in canalul Eurit care separa Eubeea de restul Greciei, diperat ca nu poate sa explice mareele, fenomen foarte sensibil in acest punct al Mediteranei, iar altii, care sunt cei mai de crezut afirma ca ar fi murit normal, de o boala de care suferise toata viata.

PARADOXELE LOGICE

Fenomenul paradoxelor (sau al antinomiilor) logice era bine cunoscut grecilor. Logicienii evului mediu au fost si ei intens preocupati de studiul paradoxelor ("insolubilelor"). Adevarata lor importanta a iesit la iveala abia odata cu descoperirea lor intr-o serie de teorii matematice (teoria multimilor lui Cantor si sistemul logico-aritmetic al lui Frege), iar apoi si in teoriile logicii.

Termenul de "paradox "poate fi definit in mai multe feluri:

1) expresie din care pot fi deduse propozitii contradictorii

2) contradictie formala dedusa intr-un sistem teoretic

3) contradictie rezultata din incercarea de a explica anumite fapte cu ajutorul unei metode date.

Pentru scopuri diferite o definitie se poate dovedi mai utila decat alta. Unul dintre cele mai cunoscute paradoxe este acela descoperit de Cantor "paradoxul multimii tuturor multimilor ".

Rezolvarea paradoxelor (constituirea unor teorii in care paradoxele date sa fie evitate) s-a facut prin diferite procedee care toate au la baza un principiu de ierarhizare a abstractiilor. Sunt cunoscute in special metodele propuse de Russel (teoria tipurilor), Hilbert, Brouwer, Bocivar, Quine.

In cele ce urmeaza nu ma voi ocupa insa de procedeele formale de rezolvare ci de aspecte filozofice ale fenomenului paradoxal.

Studiul paradoxelor nu se reduce la gasirea unor procedee de evitare a lor caci in acest caz le-am trata ca pe un fenomen de importanta locala si strict formala pentru teoria data si ar parea ca un fenomen absolut negativ pentru cunoastere. Cunoastem diferite specii de contradictii formale: sofisme, paralogisme, identificari false, paradoxe (antinomii), aporii, etc. Ele pot prezenta importanta sub cele mai diferite aspecte.

Immanuel Kant a fost primul mare filozof care s-a apropiat de intelegerea importantei deosebite a antinomiilor. "Pe pozitiile vechii metafizici ", scria Hegel, se admitea ca atunci cand cunoasterea cade in contradictii aceasta ar fi doar o ratacire intamplatoare, produsa de o greseala subiectiva in deductie si rationare. Dupa Kant insa sta in natura gandirii insasi de a cadea in contradictii (antinomii) cand vrea sa cunoasca " infinitul " .

O deosebita importanta pentru intelegerea antinomiilor stiintei prezinta observatiile facute de Marx intr-o carte de a sa 2 asupra contradictiilor economiei politice clasice engleze.

Problemele ce se impun in studiul paradoxelor privesc structura (mecanismul), cauzele si rezolvare lor.

In structura paradoxelor apar asemenea categorii ca multime, element, totalitate ( "toti "), adevar, fals, desemnare, etc. precum si unele raporturi corespunzatoare. Istoria logicii si matematicii a aratat ca dificultatile aparute vizeaza mai ales raportul acestor categorii cu absolutul si relativul precum si cu finitul si infinitul.

Care este cauza paradoxelor

Cauza lor nu poate fi doar ceva "subiectiv "caci rolul si problematica pe care au starnit-o aparitia lor in istoria matematicii si logicii sugereaza cu totul altceva.

In realitate, asa cum arata Marx in legatura cu contradictiile economiei clasice engleze, dedesubtul acestor antinomii stau probleme dificile ale cunoasterii. Gandirea cade in antinomii (paradoxe) in efortul ei de a cunoaste realitatea obiectiva. Cauza antinomiilor stiintei sta in procesul cunoasterii, proces care are la randul sau legile sale naturale ; dar gandirea nu cade in antinomii oricand si oricum.

"Criza stiintei "nu era un fenomen nou, fizica, biologia s. a, domenii stiintifice o suportasera deja.

Contradictiile formale aparute in mecanica clasica erau irezolvabile din punctul de vedere al acestei mecanici. Conceptele si principiile mecanicii trebuiau revizuite. Aceasta sarcina a fost indeplinita in mare parte de A. Einstein. In acest caz ca si in altele iesirea din "faza paradoxala "(deci din criza) a insemnat o adevarata revolutie in stiinta.

Studiind istoria stiintei putem conchide ca in cunoasterea paradoxelor sunt formele nemijlocite (concrete) pe care le iau contradictiile, ca antinomia (paradoxul) reprezinta contradictia specifica cunoasterii.

In acest fel, poarta stiintei ramane mereu deschisa contradictiilor.

TERMENII

Un termen este un cuvant sau un grup de cuvinte prin care se exprima o notiune, respectiv intelesul termenului si care se refera la unul sau mai multe obiecte despre care se afirma notiunea in cauza.

Un termen are structura urmatoarelor elemente:

1. componenta lingvistica: cuvantul sau grupul de cuvinte;
2. componenta cognitiva: notiunea;
3. componenta ontologica: multimea de obiecte.

In plan mintal se vorbeste de un anumit inteles al termenului ce constituie intensiunea termenului, iar in plan real se vorbeste de referinta termenului, ceea ce reprezinta extensiunea termenului(sfera).

CLASIFICAREA TERMENILOR

Exista mai multe tipuri de termeni ca face necesara clasificarea acestora. Criteriile de clasificare cele mai evidente sunt intensiunea si extensiunea termenilor:

Din punct de vedere intensional, termenii sa clasifica astfel:

• termeni absoluti / relativi
• termeni absoluti: numai daca se aplica obiectelor din extensiunile lor considerate izolat
• ex: planeta, obiect, culoare
• termeni relativi: in cazul in care termenul desemneaza o relatie ce se stabileste intre doua sau mai multe obiecte
• ex: unchiul meu, muschiul meu, mai mare decat
• termeni abstracti / concreti
• termeni abstracti: numai daca el desemneaza insusiri, proprietati sau relatii ca elemente de sine statatoare, independente de obiectele carora le revin acestor insusiri
• ex: frumusete, roseata, claritate
• termeni concreti: in masura in care termenul desemneaza obiecte, insusiri sau proprietati caracteristice acestora
• ex: frumos, rosu, clar
• termeni pozitivi / negativi
• termeni pozitivi: numai daca indica prezenta anumitor insusiri
• ex: coerent, prietenos
• termeni negativi: in cazul in care se indica absenta unor proprietati
• ex: stirb, orb, surd
• termeni simpli / compusi
• termeni simpli: numai daca detine rolul de notiune primara
• ex: autoturism, punct, propozitie
• termeni compusi: desemneaza derivate ale notiunilor primare
• ex: autoturism de teren, punct de vedere

Din punct de vedere extensional, termenii sa clasifica astfel:

• termeni vizi / nevizi
• termeni vizi: numai daca extensiunea sa nu contine nici un obiect
• ex cel mai mare numar prim, patrat perfect - logic vizi

centaur, sirena - factual vizi

• termeni nevizi: in caz contrar
• ex: cal, caiet, sincer
• termeni singulari / generali
• termeni singulari: numai daca se refera doar la un singur obiect (extensiunea termenului este construita dintr-un singur obiect)
• ex: Liceul "Grigore Moisil ", Timisoara
• termeni generali: in cazul in care extensiunea termenului contine cel putin doua obiecte
• ex: oras, carte, padure
• termeni colectivi / distributivi
• termeni colectivi: numai daca obiectele din extensiunea sa sunt colectii de obiecte asa incat proprietatile ce revin colectiei, nu revin fiecarui membru al colectiei
• ex: armata, biblioteca
• termeni distributivi: in cazul in care fiecare caracteristica din intensiunea termenului revine fiecarui obiect din extensiune
• ex: pom, mamifer, cana
• termeni vagi / precisi
• termeni vagi: numai daca nu se poate decide cu certitudine pentru orice obiect daca face parte sau nu din extensiunea termenului
• ex: tanar, frumos, bun
• termeni precisi: in cazul in care exista posibilitatea deciziei pentru orice obiect
• ex: patrat, fotografie, perete

RAPORTURI LOGICE INTRE TERMENI

Din punct de vedere extensional se pot preciza diferite tipuri de raporturi logice:

• raporturi de concordanta: daca extensiunile elementelor au cel putin un element comun

Prin cercetarea acestor raporturi se permite delimitarea urmatoarelor tipuri de raporturi de concordanta:

• raportul de identitate: numai in cazul in care doi termeni au in comun toate obiectele din extensiunile lor, altfel spus aceeasi extensiune

A = om

B = animal capabil sa construiasca unelte

• raportul de ordonare: numai in cazul in care oricare obiect ce apartine extensiunii unui termen, apartine si extensiunii celui de-al doilea termen, in timp ce, cel de-al doilea termen are in extensiunea sa si obiecte ce nu apartin extensiunii primului obiect

A = pisica(specie)

B = mamifer(gen)

A = specie - termen subordonat

B = gen - supraordonat

• raportul de incrucisare: numai in cazul in care extensiunile a doi termeni au in comun cel putin un obiect, fiecare termen avand in extensiunea sa si obiecte ce nu apartin extensiunii celuilalt termen

A = roman

B = inginer

• raporturi de concordanta: daca extensiunile elementelor nu au nici un element comun

Aceasta categorie cuprinde:

• raportul de contrarietate: numai in cazul in care oricare ar fi obiectul acesta nu poate apartine simultan, extensiunii ambilor termeni, existand posibilitatea de a nu apartine extensiunii nici unuia dintre ei

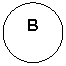
A = Africa

B = Europa

• raportul de contradictie: numai in cazul in care oricare ar fi obiectul acesta nici nu face parte, nici nu lipseste simultan din extensiunea ambilor termeni sau termenii reprezinta unul negatia celuilalt, luata sau nu intr-un univers de discurs
• OBS. : Universul de discurs reprezinta un domeniu de referinta, respectiv o categorie de obiecte de un anumit gen, gen epuizat de una sau mai multe specii.

B A = om

B = non-om

In afara unui univers de discurs.

A = legal

B= ilegal

Intr-un univers de discurs.

PRINCIPIILE LOGICII TRADITIONALE

La baza logicii traditionale stau anumite conditii formale numite principii logice sau legi da rationare. Ele nu exprima rationamente, ci conditii generale ale rationamentelor indiferent de tipul de propozitii cu care formulam inferenta.

Fiecare rationament trebuie sa respecte simultan urmatoarele principii logice:

Principiul identitatii care presupune ca un obiect este identic numai cu sine insusi, in acelasi timp si sub acelasi raport.

A _idA(Formula va fi citita: A este identic cu A)

Regula: Orice obiect este presupus neschimbat in raport cu timpul si cu unghiul de vedere considerat, adica ramane acelasi pe tot parcursul rationamentului.

Principiul non-contradictiei presupune ca un obiect nu poate sa fie in acelasi timp si sub acelasi raportsi A, si non-A.

Formula:~(A&A`)se citeste nu sunt simultan adevarate si A, si A`.

Principiul tertulu iexclus presupune ca sau este acceptata o propozitie A, sau este respinsa dintr-un sistem de propozitii, a treia posibilitate fiind exclusa.

Principiul ratiunii suficiente presupune ca pentru a accepta sau pentru a respinge o propozitie trebuie sa dispunem de o ratiune suficienta sau altfel spus, de un temei satisfacator. Exista 4 tipuri de temeiuri:

Nici necesare si nici suficiente;

Necesare, dar nu si suficiente;

Suficiente, dar nu si necesare;

Necesare si suficiente.

Spunem ca propozitia p este un temei necesar pentru propozitia q, atunci cand fara adevarul lui p nu se poate dovedi adevarul lui q, iar daca p este un temei suficient pentru q inseamna ca admitand adevarul lui p devine imposibil ca q sa nu fie adevarata.