| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Definitie. Doua drumuri netede ![]() ,
, ![]() se numesc echivalente, cu aceeasi orientare si vom scrie (I, r) ~ (J, r1),
daca exista functia l : I
→ j, bijectiva, strict
crescatoare, de clasa C1
cu l'(t) ¹ t I I,
astfel incat r = r1 ◦ l. Functia l se numeste schimbare de parametru.
se numesc echivalente, cu aceeasi orientare si vom scrie (I, r) ~ (J, r1),
daca exista functia l : I
→ j, bijectiva, strict
crescatoare, de clasa C1
cu l'(t) ¹ t I I,
astfel incat r = r1 ◦ l. Functia l se numeste schimbare de parametru.
Exemple.
1) Drumurile netede ![]() , r(t) = (cost, sint) si
, r(t) = (cost, sint) si 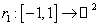 ,
, ![]() sunt echivalente cu
aceeasi orientare. Este suficient sa luam in definitia de mai sus l l(t)
= -cost.
sunt echivalente cu
aceeasi orientare. Este suficient sa luam in definitia de mai sus l l(t)
= -cost.
2) Orice drum neted ![]() este echivalent cu
drumul
este echivalent cu
drumul ![]() ,
,
![]() .
.
3) Drumurile ![]()
![]() ,
, ![]() , au acelasi suport si anume cercul cu centrul in origine, de
raza 1, dar nu sunt echivalente.
, au acelasi suport si anume cercul cu centrul in origine, de
raza 1, dar nu sunt echivalente.
Intr-adevar, se poate constata ca nu exista o functie bijectiva l : [0, 2π] → [0, 2π] astfel incat r1 = r2 ◦ l
Devinitie. Fie ![]() . Se numeste curba
parametrizata de clasa Ck,
. Se numeste curba
parametrizata de clasa Ck,
![]() (sau
(sau ![]() ). Multimea r(I) se numeste urma (imaginea, suportul) curbei.
). Multimea r(I) se numeste urma (imaginea, suportul) curbei.
Prezentam cateva moduri concrete de reprezentare a unei curbe:
1. Reprezentarea parametrica
Curba data de ecuatiile parametrice:
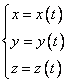 , t I I. (2.1)
, t I I. (2.1)
1. Reprezentarea implicita
Fie ![]() o multime deschisa si
o multime deschisa si ![]() . Multimea
. Multimea
![]()
reprezinta o curba daca are loc teorema urmatoare:
Teorema 2.2. Daca M0(x0, y0, z0) I Γ si in acest punct rangul matricei jacobiene
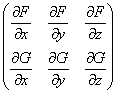 (2.3)
(2.3)
este 2, atunci exista o vecinatate W a punctului M0,
astfel incat ![]() este urma unei curbe.
este urma unei curbe.
Demonstratie. Sa presupunem ca 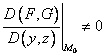 . Conform teoremei functiilor implicite, exista o vecinatate
deschisa I a punctului x0 si o vecinatate deschisa U V
a punctului (y0, z0), precum si functiile
implicite f : I → U, g : I
→ V, f, g I C1(I), astfel incat
. Conform teoremei functiilor implicite, exista o vecinatate
deschisa I a punctului x0 si o vecinatate deschisa U V
a punctului (y0, z0), precum si functiile
implicite f : I → U, g : I
→ V, f, g I C1(I), astfel incat
![]()
Observatie. Daca rangul matricei (2.3) este 2 in orice punct din Γ, atunci din teorema 2.2 rezulta ca Γ este 'local' urma unei curbe parametrizate. In acest caz ecuatiile
 (2.4)
(2.4)
se numesc ecuatii implicite ale curbei, curba obtinandu-se ca intersectia a doua suprafete.
Exemplu. Curba lui Vivianu. Este curba care se obtine intersectand o sfera cu cilindrul drept a carui baza este un cerc avand diametrul egal cu raza sferei. Portiunea de curba din semispatiul z > 0 este reprezentata in fig. 2.1.
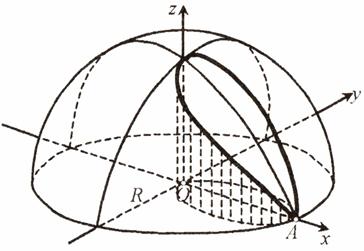
Fig. 2.1.
Asadar
![]() ,
,
deci ![]() . Matricea
. Matricea ![]() are rangul 2 pentru
orice punct diferit de (R, 0, 0).
Atunci, pentru orice astfel de punct, exista o vecinatate W astfel incat
are rangul 2 pentru
orice punct diferit de (R, 0, 0).
Atunci, pentru orice astfel de punct, exista o vecinatate W astfel incat ![]() este urma curbei.
este urma curbei.
O curba se numeste plana daca exista un plan care contine imaginea acestei curbe. Vom alege reperul cartezian, astfel incat planul curbei sa coincida cu planul xOy.
1. Reprezentarea parametrica
In acest caz, curba este data de ecuatiile parametrice:
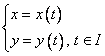 (2.5)
(2.5)
Exemple.
1) Cicloida. Este o curba de origine mecanica. In planul xOy se considera un cerc 'material' de raza a situat in semiplanul superior, tangent in O la axa Ox (fig. 2.2).
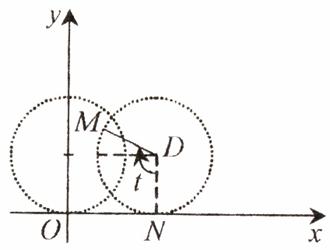
Fig. 2.2
Fie M = O.
Cicloida este curba descrisa de punctul M,
cand cercul se rostogoleste fara alunecare pe semiaxa pozitiva Ox. Punctul M va atinge axa Ox de o
infinitate de ori, distanta dintre doua puncte consecutive fiind egala cu
lungimea cercului. Pentru a stabili ecuatiile parametrice ale cicloidei, sa
consideram o noua pozitie a cercului, N
fiind noul punct de contact al cercului cu axa Ox si D centrul acestui
cerc. Alegem ca parametru t masura in
radiani a unghiului NDM. Fie M(x,
y). ![]() . Astfel, ecuatiile parametrice ale cicloidei sunt
. Astfel, ecuatiile parametrice ale cicloidei sunt
x = a(t - sin t), y = a(1 - cost), t
Sa reprezentam
grafic cicloida. Pentru a determina intersectiile cu axele de coordonate
rezolvam ecuatiile x(t) = 0, y(t) = 0. Sa remarcam ca x(t)
= 0 implica t = 0, iar din y(t)
= 0 rezulta ![]() ,
, ![]() . Asadar, cicloida trece prin origine si intersecteaza
semiaxa pozitiva Ox in punctele de
abscise x(tk) = 2kπa. Studiem variatia functiilor x(t)
si y(t). Avem x'(t) = a(1
- cost),
. Asadar, cicloida trece prin origine si intersecteaza
semiaxa pozitiva Ox in punctele de
abscise x(tk) = 2kπa. Studiem variatia functiilor x(t)
si y(t). Avem x'(t) = a(1
- cost),
y'(t) = asint. Alcatuim tabloul de variatie:
|
t |
0 π 2π 3π 4π . +∞ |
|
x'(t) |
0 + + + 0 + + + 0 + |
|
x(t) |
0 |
|
y'(t) |
0 + 0 - 0 + 0 - 0 . |
|
y(t) |
0 |
In ceea ce
priveste asimptotele, sa observam ca nu exista t I
[0, ∞), astfel incat ![]() sa fie finita si, deci
nu exista asimptote verticale. Pe de alta parte , x → +∞, cand t
→ +∞, dar
sa fie finita si, deci
nu exista asimptote verticale. Pe de alta parte , x → +∞, cand t
→ +∞, dar ![]() nu exista. Asadar, nu
exista asimptote orizontale. Deoarece
nu exista. Asadar, nu
exista asimptote orizontale. Deoarece ![]() , nu exista nici asimptote oblice. Alura cicloidei este data
in fig. 2.3.
, nu exista nici asimptote oblice. Alura cicloidei este data
in fig. 2.3.
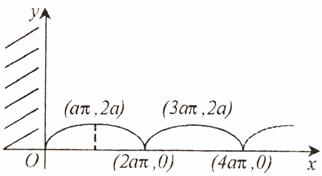
Fig. 2.3
2) Foliul lui Descartes. Are ecuatiile parametrice
 , t ¹ -1 (2.6)
, t ¹ -1 (2.6)
Intersectia
imaginii curbei cu axele de coordonate este originea axelor de coordonate
(t = 0). Prin calcul obtinem 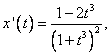
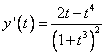 . Sa remarcam ca
. Sa remarcam ca ![]() ,
, ![]() , deci nu exista asimptote verticale si orizontale. Totodata
, deci nu exista asimptote verticale si orizontale. Totodata
![]()
![]()
Asadar, dreapta ![]() este asimptota oblica.
este asimptota oblica.
Tabloul de varitie este:
|
t |
-∞ -1 0 |
|
x'(t) |
+ + | + + + 0 - - - |
|
x(t) |
0 |
|
y'(t) |
- - | - 0 + + + 0 - |
|
y(t) |
0 |
Alura curbei este cea din fig. 2.4.
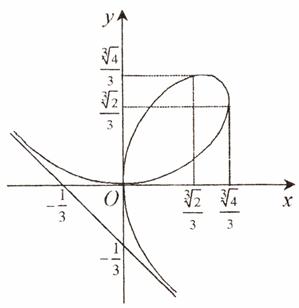
Fig. 2.4.
2. Reprezentarea explicita
Fie ![]() , f I C (I).
Graficul sau Gf
= este urma drumului parametrizat
, f I C (I).
Graficul sau Gf
= este urma drumului parametrizat ![]() , de ecuatii parametrice
, de ecuatii parametrice
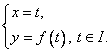
Aceste curbe au fost studiate in liceu.
3. Reprezentarea implicita
Fie ![]() o multime deschisa si
o multime deschisa si ![]() , F I C (D).
Multimea
, F I C (D).
Multimea
Γ (2.7)
se numeste curba plana de clasa C1 avand ecuatia carteziana
F(x, y) = 0
Un punct (x0, y0) I Γ se numeste singular daca
![]()
Teorema urmatoare precizeaza sensul in care Γ este o curba.
Teorema 2.3. Fie (x0, y0) I Γ, astfel incat
grad![]() .
.
Exista o vecinatate V a punctului (x0, y0), astfel incat ![]() este urma unei curbe.
este urma unei curbe.
Demonstratie. Folosim teorema functiilor implicite. Daca, de exemplu,

atunci exista o vecinatate deschisa I a punctului x0 si o vecinatate deschisa U a punctului y0, astfel incat V = I U Ì D, precum si functia unic determinata f : I → U, f I C (I), astfel incat
![]()
In concluzie, local, putem gasi un drum parametrizat neted avand acelasi suport cu Γ
Exemple.
1) Fie ![]()
![]() , unde a > 0, b > 0. Dupa cum se stie, in acest caz, ecuatia F(x,
y) = 0 este ecuatia unei elipse de
semiaxe a, b, relativ la reperul dat de axele de simetrie ale elipsei.
Multimea (2.7) este curba in sensul teoremei 2.3. Intr-adevar, daca grad F(x0, y0)
=
, unde a > 0, b > 0. Dupa cum se stie, in acest caz, ecuatia F(x,
y) = 0 este ecuatia unei elipse de
semiaxe a, b, relativ la reperul dat de axele de simetrie ale elipsei.
Multimea (2.7) este curba in sensul teoremei 2.3. Intr-adevar, daca grad F(x0, y0)
= ![]() ,
rezulta ca x0 = 0, y0 = 0. Dar (0, 0)
,
rezulta ca x0 = 0, y0 = 0. Dar (0, 0) ![]() , deci grad F(x0, y0)
¹
, deci grad F(x0, y0)
¹ ![]() (x0, y0)
I Γ. Prin urmare, teorema 2.3 se poate aplica.
(x0, y0)
I Γ. Prin urmare, teorema 2.3 se poate aplica.
2) Sa consideram multimea ![]() . Se
constata ca (0, 0) este punct singular. Pentru a obtine o reprezentare
parametrica a curbei, vom intersecta curba cu dreapta y = tx. Daca x = 0, se obtine punctul singular (0,
0). Pentru t ¹ -1, se obtin ecuatiile (2.6), adica ecuatiile
parametrice ale foliului lui Descartes.
. Se
constata ca (0, 0) este punct singular. Pentru a obtine o reprezentare
parametrica a curbei, vom intersecta curba cu dreapta y = tx. Daca x = 0, se obtine punctul singular (0,
0). Pentru t ¹ -1, se obtin ecuatiile (2.6), adica ecuatiile
parametrice ale foliului lui Descartes.
4. Reprezentarea in coordonate polare
Ecuatia unei curbe in coordonate polare este de forma
![]()
unde ρ si θ sunt coordonatele polare ale unui punct
din plan, iar ![]() este o functie derivabila. In acest caz, f(θ) este coordonata ρ. In consecinta, curba are ecuatiile parametrice
este o functie derivabila. In acest caz, f(θ) este coordonata ρ. In consecinta, curba are ecuatiile parametrice
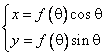
![]() (2.8)
(2.8)
Exemple.
1) Spirala lui Arhimede. Este curba plana de ecuatie ρ = aθ θ 0, a > 0. Deoarece
) = a > 0, )
creste cand
creste. Cum reprezentarea parametrica este ![]()
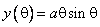 , rezulta ca graficul intersecteaza axele de
coordonate cand ia
valorile 0,
, rezulta ca graficul intersecteaza axele de
coordonate cand ia
valorile 0, ![]() . Graficul este o spirala. Tinand seama de
urmatorul tabou de variatie
. Graficul este o spirala. Tinand seama de
urmatorul tabou de variatie
|
q |
0 |
|
ρ'(q) |
+ + + + + + + + + + + |
|
ρ(q) |
0 |
alura acestei spirale este cea din fig. 2.5.
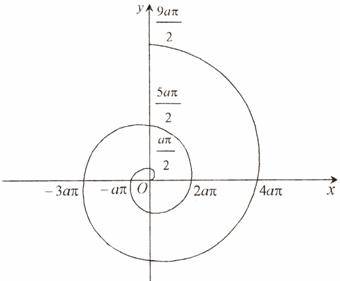
Fig. 2.5.
2) Rozeta cu
trei foi. Este
curba de ecuatie ![]() .
Conditia ρ 0 este satisfacuta pe [0, 2p] pentru
.
Conditia ρ 0 este satisfacuta pe [0, 2p] pentru ![]() . Daca doua
valori ale lui q difera print-un multiplu de 2p este
acelasi, deci punctele corespunzatoare coicid. Deoarece q) = -3asin3q,
tabloul de variatie este
. Daca doua
valori ale lui q difera print-un multiplu de 2p este
acelasi, deci punctele corespunzatoare coicid. Deoarece q) = -3asin3q,
tabloul de variatie este
|
q |
0 |
|
ρ'(q) |
- - - | / / |+ + 0 - - | / / |
|
ρ(q) |
a |
|
q |
p |
|
ρ'(q) |
/ / |+ + 0 - -| / / |+ + 0 |
|
ρ(q) |
/ / |0 |
iar graficul este:
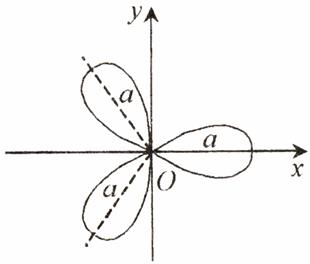
Fig. 2.6.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2444
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved