| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Indicatorii STATISTICI
Necesitatea folosirii indicatorilor statistici
Indicatori statistici primari si derivati
Indicatori in marimi absolute si in marimi relative
1 Necesitatea folosirii indicatorilor statistici
Obiectul de studiu al statisticii il formeaza fenomenele si procesele de masa, a caror proprietate principala este variabilitatea formelor individuale de manifestare in timp, in spatiu si sub raport organizatoric.
In sensul cel mai larg, indicatorul statistic este expresia numerica a unor fenomene, procese activitati sau categorii economice si socilae, definite in timp, spatiu si calitativ.
Obtinuti in cadrul unor cerecetari statistice concrete, indicatorii statistici sunt purtatori de informatii avand continut real, obiectiv determinat.
Indicatorii statistici indeplinesc in cerecetarea statistica o serie de functii, cum ar fi:
Functia de masurare, care deriva din particularitatile statisticii, ca stiinta care porneste intotdeauna de la cunoasterea empirica a fenomenelor, iar prin generalizare, la cunoasterea esentei acestora. In urma acestei operatii se obtin indicatorii absoluti care masoara o colectivitate statistica.
Functia de comparare, provine din faptul ca statistica opereaza cu fenomene variabile, ceea ce necesita cunoasterea modificarilor intervenite ca nivel de dezvoltare sau ca structura. Compararea se face fie ca diferenta, fie sub forma de raport. De aici rezulta indicatorii derivati.
Functia de analiza, provine din faptul ca statistica opereaza in mod frecvent cu diferite variabile complexe care se pot descompune fie intr-un produs de mai multi factori, fie intr-o suma de mai multe elemente componente. In ambele cazuri este necesar sa se analizeze relatiile care exista intre fiecare parte si intreg, intre fiecare factor si rezultat.
Functia de sinteza, este specifica fenomenului care se manifesta diferit de la o unitate la alta. De regula, se calculeaza indicatori sub forma de valori medii.
Functia de estimare, este specifica metodei statistice si poate sa se foloseasca pentru masurarea tendintei de dezvoltare a fenomenului in aceeasi perioada de timp, variabila ca spatiu sau calitativ sau in aceleasi conditii de spatiu si calitativ, dar variabile in timp.
Functia de verificare a ipotezelor si de testare a semnificatiilor unor indicatori, este aplicata in interpretarea statistica a fenomenelor economice si sociale.
Verificarea ipotezelor conduce la folosirea indicatorilor care nu au atasate o singura valoare, ci un interval de valori.
Functiile indicatorilor statistici stau la baza clasificarii lor.
Indicatori statistici primari si derivati
Dupa etapa in care apar in procesul de cunoastere statistica, indicatorii statistici sunt:
Indicatori primari, se obtin in cadrul prelucrarii primare a datelor statistice ca urmare a procesului de centralizare a datelor unei observari statistice. Ei au continut concret si forma concreta de exprimare. Ei constituie baza informationala a cunoasterii statistice. De regula, acesti indicatori sunt inclusi in analiza statistica pe toate structurile organizatorice ale economiei nationale.
In practica se pot intalni mai multe categorii de indicatori primari:
indicatori primari care se obtin de regula la nivelul unitatilor complexe ca suma a unor componente;
indicatori primari obtinuti prin agregarea unor valori individuale cu acelasi continut calculat pe treptele ierarhice inferioare;
indicatori primari obtinuti direct din observare, atunci cand se face un studiu monografic a unei unitati statistice.
Ca o trasatura caracteristica a acestor indicatori primari se remarca faptul ca elementele lor constitutive se regasesc la nivelul tuturor unitatilor folosite la culegerea datelor.
Indicatori derivati, se obtin in faza de prelucrare statistica a marimilor absolute prin aplicarea diferitelor metode si procedee de calcul statistic. Indicatorii derivati fac posibila analiza aspectelor calitative ale fenomenelor si proceselor cercetate. Ei exprima relatii cantitative dintre diferite caracteristici statistice, dintre diferitele parti ale unei colectivitati sau dintre fenomenele ce se gasesc intr-un anumit grad de interdependenta.
De regula, indicatorii derivati se obtin prin aplicarea unui model de calcul statistic de comparare sau de estimare.
Modelele de estimare sunt folosite in statistica pentru a putea masura gradul de influenta a diferitilor factori asupra fenomenului analizat.
Indicatorii derivati au un caracter abstract, chiar daca uneori se exprima in unitati specifice de masura. Acestia sunt extrem de numerosi si cu metdologii variate de calcul sub forma de marimi relative, marimi medii, indicatori ai variatiei, indici, indicatori ce caracterizeaza corelatia.
Indicatori in marimi absolute si in marimi relative
Indicatori in marimi absolute
In urma sistematizarii datelor, prin centralizare si grupare, se obtin indicatori primari. Pe baza lor, prin diferite procedee statistice de comparare, abstractizare si generalizare, se obtin indicatorii derivati.
Prin indicatorii primari se prezinta, sub forma de marimi absolute, volumul unui ansamblu de unitati sau valoarea unei caracteristici, pe total sau pe grupe.
In statistica, marimile absolute reprezinta valori definite prin ele insele, independent de orice sistem de referinta. Sunt folosite pentru exprimarea indicatorilor de nivel si ai variatiei absolute.
a) Indicatorii de nivel exprima aspectul cantitativ al fenomenelor, volumul unui ansamblu sau valoarea unei caracteristici. Indicatorii de nivel se determina ca:
indicatori individuali se obtin in urma unei inregistrari statistice si exprima valoarea caracteristicii observate la nivelul fiecarei unitati statistice.
Indicatori sintetici reprezinta rezultatul centralizarii pe grupe sau pe ansamblul colectivitatii.
Insumarea directa a elementelor considerate in calculul indicatorilor sintetici este posibila doar pentru elemente omogene.
b) Indicatorii variatiei absolute se obtin prin compararea, sub forma de scadere, a 2 nivele ale aceluiasi indicator.
Variatia
absoluta, numita si spor,
se simbolizeaza ![]() si se
calculeaza pentru variabila xi la momentele T0
si T1, astfel:
si se
calculeaza pentru variabila xi la momentele T0
si T1, astfel:
![]() ,
,
sau
in general: ![]()
Indicatorii exprimati in marimi absolute, individuali sai sintetici, au o fera de comparabilitate redusa.
Indicatori in marimi relative
Marimile relative exprima rezultatul compararii, sub forma de raport, a doi indicatori statistici si arata cate unitati din indicatorul de la numarator revin la o unitate a indicatorului considerat ca baza de raportare.
Obtinerea marimilor relative presupune rezolvarea a trei probleme principale:
alegerea bazei de comparare se face in functie de gradul de interdependenta dintre caracteristicile sau fenomenele comparate sau in functie de scopul cercetarii.
asigurarea comparabilitatii datelor care formeaza raportul cere ca indicatorii comparati sa fie marimi comparabile.
alegerea formei de exprimare a marimilor relative pp. exprimarea sub forma de coeficienti sau de procente.
Exprimarea sub forma de coeficienti este folosita cand indicatorii comparati dau un rezultat exact sau sunt valori apropiate. Arata de cate ori se cuprinde indicatorul de raportat in baza de raportare.
Exprimarea sun forma de procente (sau promile) este folosita cand indicatorul de raportat este mult prea mic fata de baza pentru ca raportul sa fie sugestiv.
In analiza statistica se utilizeaza diferite tipuri de marimi relative:
marimi relative de structura
marimi relative de corespondenta
marimi relative de intensitate
marimi relative de variatie.
Marimile relative de structura
Calculul acestor marimi este impus de necesitatea cunoasterii aprofundate a compozitiei acelor colectivitati care au fost separate in grupe sau subgrupe dupa variatia uneia sau mai multor caracteristici de grupare. Ele exprima raportul dintre parte si intreg si arata ponderea partii, grupei fata de totalul colectivitatii.
Intr-o serie statistica atributiva, intr-o serie
teritoriala sau pentru o variabila statistica construita pe
baza unor componente, ponderea sau greutatea specifica a unui element
(xi) in totalul colectivitatii (![]() ) se obtine pe baza relatiei:
) se obtine pe baza relatiei:
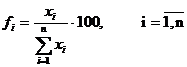
Marimile relative de corespondenta
Denumite si marimi relative de coordonare, marimile relative de corespondenta caracterizeaza raportul numeric in care se gasesc doi indicatori de acelasi fel, apartinand unor grupe ale aceleiasi colectivitati statistice sau unor colectivitati statistice de acelasi fel, dar situate in spatii diferite.
Aceste marimi exprima cate unitati din grupa revin la 100, respectiv 1000 de unitati din cealalta grupa.
Marimile relative de intensitate
Considerate caracteristici derivate, in statistica, marimile relative de intensitate se obtin prin raportarea a doi indicatori absoluti de natura diferita care se afla intr-o relatie de interdependenta.
Marimile relative de intensitate sunt exprimate in unitatile concrete de masura ale celor doua variabile. Aceste marimi evidentiaza gradul, intensitatea de raspandire a fenomenului in raport cu variabila la care se raporteaza. Sunt utilizate in diverse domenii: demografic, economic etc.
In demografie se utilizeaza pentru caracterizarea miscarii populatiei. De ex., pentru caracterizarea miscarii naturale a populatiei se calculeaza raportul dintre numarul nasterilor, al deceselor, sporul natural si numarul populatiei dintr-o zona, la un moment dat.
In economie se utilizeaza pentru caracterizarea gradului de dotare, de inzestrare tehnica a muncii, pentru calculul productivitatii muncii si, in general, pentru determinarea indicatorilor de eficienta economica.
In domeniul social-cultural se utilizeaza pentru caracterizarea nivelului de trai.
In cazul in care diferenta dintre indicatorii raportati (ca marime) este prea mare, pentru a obtine un rezultat semnificativ, raportul se inmulteste fie cu 1000, fie cu 10000.
Marimile relative de variatie
Numite si marimi relative ale dinamicii, ritmuri sau indicii dinamicii, exprima variatia relativa a unei variabile intre doua momente sau perioade considerate, perioada curenta sau efectiva, notata cu 1 si perioada de baza, notata cu zero.
In functie de complexitatea fenomenului studiat, se pot calcula:
indici elementari descriu variatia relativa a unei singure valori.
indici sintetici permit descrierea unui ansamblu de valori.
Ex. Marimi relative de structura
Transportul de marfuri, pe moduri de transport, in anul 2002:
|
Categorii de transport |
Mii t marfa |
|
-transp. feroviar -transp. rutier -transp. fluvial -transp. maritim -transp. aerian -transp. prin conducte | |
|
Total |
Sursa: ASR, 2001, pg. 515
Sa se calculeze marimile relative de structura.
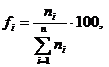
pt. transp. feroviar: ![]() ,
,
- pt. transp. rutier: ![]()
- pt. transp. fluvial: ![]()
- pt. transp. maritim: ![]()
- pt. transp. aerian: ![]()
- pt. transp. prin conducte: ![]()
Proprietatea: 18,12+74,31+3,51+1,07+0,002+2,988=100%
Ex. Marimi relative de corespondenta
Gruparea salariatilor unei firme, pe sexe:
|
Grupe de sal. pe sexe |
Nr. sal. |
|
-femei -barbati |
Sa se calculeze marimile relative de corespondenta.
pt. femei =![]() la 1000 barbati
la 1000 barbati
pt. barbati =![]() la 1000 femei.
la 1000 femei.
Ex. Marimi relative de intensitate
Miscarea naturala a populatiei in 1998 se caracterizeaza prin urmatoarele date:
|
Indicatori |
Numar |
|
-nascuti-vii -decese -casatorii -divorturi -nascuti-morti -decese la varsta sub 1 an |
Sursa: ASR 1999, pg. 74
Sa se calculeze marimile relative de intensitate posibile, stiind ca nr. populatiei era de 22.502.803 locuitori.
coef. de natalitate =![]()
coef. de mortalitate =![]()
coef. de nuptialitate =![]()
coef. de divorturilor =![]()
coef. morti-natalitate =![]()
coef. mortalitatii
infantile=![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3778
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved