| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Aria unei suprafete plane marginita de o curba.
Proprietatile functiilor integrabile.
Fie ![]() o functie continua, pozitiva
si crescatoare in intervalul
o functie continua, pozitiva
si crescatoare in intervalul ![]() . Graficul acestei
functii este un arc de curba situat deasupra axei 0x. Ne propunem sa calculam
aria trapezului mixtiliniu
. Graficul acestei
functii este un arc de curba situat deasupra axei 0x. Ne propunem sa calculam
aria trapezului mixtiliniu ![]() . In acest scop vom
construi un sir de poligoane exterioare si un sir de poli-goane
interioare de o forma anumita, care ne vor duce la rezultat. Sa
impartim intervalul
. In acest scop vom
construi un sir de poligoane exterioare si un sir de poli-goane
interioare de o forma anumita, care ne vor duce la rezultat. Sa
impartim intervalul ![]() prin punctele
prin punctele ![]()
![]() in n
subintervale, iar prin aceste puncte sa ducem paralele la axa 0y, paralele care taie arcul
in n
subintervale, iar prin aceste puncte sa ducem paralele la axa 0y, paralele care taie arcul ![]() in punctele
in punctele ![]() astfel incat trapezul mixtiliniu
astfel incat trapezul mixtiliniu ![]() apare ca o reuniune a n trapeze mixtilinii
apare ca o reuniune a n trapeze mixtilinii
![]()
Daca notam
![]()
atunci aria totala A
este suma ariilor elementare ![]()
A =![]()
Aria ![]() a trapezului
mixtiliniu
a trapezului
mixtiliniu ![]() este cuprinsa
intre aria dreptunghiului exterior
este cuprinsa
intre aria dreptunghiului exterior ![]() si a
dreptunghiului interior
si a
dreptunghiului interior ![]() ; daca
notam cu
; daca
notam cu ![]() si
si ![]() aceste doua arii
aceste doua arii
![]()
![]()
urmeaza ca avem neegalitatile
![]()
insumand, obtinem
![]()
unde
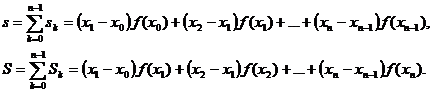
Sumele s si S se numesc sumele lui Darboux.
Sa observam ca S
este aria poligonului exterior, obtinut ca reuniunea dreptunghiurilor exterioare ![]() , iar s este aria poligonului interior
obtinut ca reuniunea dreptunghiuri-lor interioare
, iar s este aria poligonului interior
obtinut ca reuniunea dreptunghiuri-lor interioare ![]() corespunzatoare diviziunii
corespunzatoare diviziunii ![]()
Inainte de a merge mai departe, sa definim cateva notiuni.
a) Fie ![]() un interval inchis
si marginit. O familie unita de puncte
un interval inchis
si marginit. O familie unita de puncte ![]()
![]()
se
numeste o diviziune a intervalului ![]() . Un interval oarecare
. Un interval oarecare ![]() al diviziunii se
numeste interval partial sau subinterval.
al diviziunii se
numeste interval partial sau subinterval.
b) Vom numi norma diviziunii ![]() numarul pozitiv
numarul pozitiv
![]()
adica lungimea celui mai mare
interval partial al diviziunii d;
deci pentru orice ![]() avem
avem
![]()
c) Vom spune ca o diviziune ![]() a intervalului
a intervalului ![]() este mai fina decat diviziunea d si se scrie
este mai fina decat diviziunea d si se scrie ![]() sau
sau ![]() daca toate punctele diviziunii d apartin diviziunii
daca toate punctele diviziunii d apartin diviziunii ![]() (care contine si alte puncte). Daca
(care contine si alte puncte). Daca
![]() este mai fina
decat d, atunci
este mai fina
decat d, atunci
![]() (1)
(1)
Reciproca nu este insa in general adevarata, adica
neegalitatea (1) nu atrage incluziunea ![]() , deoarece diviziunea
, deoarece diviziunea ![]() poate fi formata
din intervale partiale mai mici decat ale divi-ziunii d, fara ca toate punctele diviziunii d sa apartina diviziunii
poate fi formata
din intervale partiale mai mici decat ale divi-ziunii d, fara ca toate punctele diviziunii d sa apartina diviziunii ![]() .
.
Sa consideram acum un sir
de diviziuni ![]() ordonate dupa
relatia de finete
ordonate dupa
relatia de finete
![]()
prin urmare normele lor formeaza sirul descrescator
![]()
Sa cerem ca ![]() In aceste conditii, sirul sumelor s
In aceste conditii, sirul sumelor s
![]()
si al sumelor S
![]()
sunt convergente catre o limita comuna care este aria
trapezului mixtiliniu ![]() . Intr-adevar, avem
. Intr-adevar, avem
![]()
deci si
![]() . (2)
. (2)
Functia ![]() fiind continua in intervalul
fiind continua in intervalul ![]() este uniform
continua in
este uniform
continua in ![]() , deci pentru orice numar
, deci pentru orice numar ![]() exista un
numar
exista un
numar ![]() astfel incat sa
avem
astfel incat sa
avem
![]()
oricare ar fi ![]() , care satisfac neegalitatea
, care satisfac neegalitatea
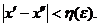
Sa consideram acum numarul N astfel incat pentru ![]() toate diviziunile
toate diviziunile ![]() sa indepli-neasca
conditia
sa indepli-neasca
conditia
![]()
fapt ce este posibil, deoarece ![]() cand
cand ![]() . Deci pentru doua puncte consecutive oa-recare
. Deci pentru doua puncte consecutive oa-recare ![]() ale unei diviziuni
ale unei diviziuni ![]() , avem
, avem
![]()
deoarece ![]() deci si
deci si ![]() Cu aceste rezultate, neegalitatea (2) se scrie
Cu aceste rezultate, neegalitatea (2) se scrie
![]()
de unde rezulta imediat ca ![]() si
si ![]() au aceeasi
limita, anume aria A a
trapezului curbiliniu
au aceeasi
limita, anume aria A a
trapezului curbiliniu ![]() .
.
Numarul A se numeste si integrala
definita a functiei ![]() in intervalul
in intervalul ![]() si se
noteaza
si se
noteaza
A=![]()
(se citeste integrala de la a
la b din ![]() ). Semnul
). Semnul ![]() se numeste semnul de integrare; a, b se numesc limitele
de integrare, a limita
inferioara si b limita
superioara. Intervalul
se numeste semnul de integrare; a, b se numesc limitele
de integrare, a limita
inferioara si b limita
superioara. Intervalul ![]() se numeste interval de integrare, iar
se numeste interval de integrare, iar ![]() functia de integrat sau integrant.
functia de integrat sau integrant.
In continuare ne vom ocupa de convergenta sumelor ![]() si
si ![]() in conditii mai largi pentru functia
in conditii mai largi pentru functia
![]()
Fie ![]() o functie marginita,
definita pe un interval
o functie marginita,
definita pe un interval ![]()
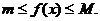
Sa impartim intervalul ![]() in n subintervale prin punctele
in n subintervale prin punctele ![]()
![]() . Notam cu
. Notam cu ![]() marginile
superioara si inferioara ale functiei
marginile
superioara si inferioara ale functiei ![]() in intervalul
in intervalul ![]() .
.
Aria ![]() a trapezului
mixtiliniu
a trapezului
mixtiliniu ![]() este cuprinsa
intre ariile dreptunghiului exterior
este cuprinsa
intre ariile dreptunghiului exterior ![]() si interior
si interior ![]() , deci
, deci
![]()
insumand in raport cu ![]() , obtinem
, obtinem
![]()
unde
![]()
sumele S si s se numesc tot sumele lui Darboux relative la diviziunea considerata, s este suma inferioara Darboux, iar S suma superioara Darboux si au urmatoarele proprietati:
![]() .
.
Intr-adevar, pentru orice interval ![]() avem
avem
![]()
deci si
![]()
din care prin insumare obtinem
![]()
deci
![]() .
.
Daca
![]() este un punct oarecare
al intervalului
este un punct oarecare
al intervalului ![]() si
si ![]() suma
suma
![]()
atunci
![]() (1)
(1)
Intr-adevar, pentru orice ![]() avem
avem
![]()
deoarece ![]() sunt marginile functiei
in intervalul
sunt marginile functiei
in intervalul ![]() ; daca
inmultim cu
; daca
inmultim cu ![]() si insumam
rezulta neegalitatile (1). Sumele
si insumam
rezulta neegalitatile (1). Sumele ![]() se numesc sume Riemann
rela-tiv la diviziunea considerata.
se numesc sume Riemann
rela-tiv la diviziunea considerata.
Sa
observam ca pentru o diviziune data d avem o infinitate de sume ![]() , insa numai doua sume Darboux
, insa numai doua sume Darboux ![]() si
si ![]() .
.
Intre sumele Riemann si sumele Darboux ale unei diviziuni d avem urmatoarele relatii
![]()
![]()
Intr-adevar, fie ![]() ; in orice
interval partial
; in orice
interval partial ![]() exista un punct
exista un punct ![]() astfel incat sa avem
astfel incat sa avem
![]()
daca alegem pentru suma ![]() punctele
punctele ![]() care indeplinesc
aceasta conditie, ob-tinem
care indeplinesc
aceasta conditie, ob-tinem
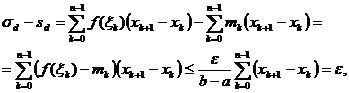
deci
![]()
de unde
rezulta ca ![]() Pentru egalitatea a
doua se procedeaza in mod asema-nator.
Pentru egalitatea a
doua se procedeaza in mod asema-nator.
Daca diviziunea ![]() este mai fina decat diviziunea d, atunci
este mai fina decat diviziunea d, atunci
![]()
adica sumele inferioare cresc, iar sumele superioare descresc daca trecem de la o diviziune la o alta diviziune mai fina.
Daca ![]() este un subinterval al diviziunii d, atunci punctele
este un subinterval al diviziunii d, atunci punctele ![]() apartin si diviziunii
apartin si diviziunii ![]() insa in intervalul
insa in intervalul ![]() pot sa existe si alte puncte ale
diviziunii
pot sa existe si alte puncte ale
diviziunii ![]() , fie
, fie
![]()
Daca ![]() sunt marginile
inferioara si superioara ale functiei
sunt marginile
inferioara si superioara ale functiei ![]() in intervalul
in intervalul ![]() , atunci
, atunci
![]()
deci si
![]()
insumand acum in raport cu indicii k obtinem
![]()
Oricare
ar fi diviziunile ![]() si
si ![]() avem
avem
![]()
adica orice suma inferioara este mai mica sau cel mult egala cu o suma superioara.
Sa consideram diviziunea d formata din toate punctele
diviziunilor ![]() si
si ![]() . Diviziunea d va fi mai fina decat diviziunea
. Diviziunea d va fi mai fina decat diviziunea ![]() sau
sau ![]() , prin urmare,
conform proprietatii 4, avem
, prin urmare,
conform proprietatii 4, avem
![]()
si
![]()
de unde
![]()
sau
![]() (2)
(2)
Daca
D este multimea tuturor
subdiviziunilor intervalului ![]() , atunci
, atunci
![]()
cum rezulta imediat din neegalitatea (2).
Multimea ![]() este
marginita superior, iar multimea
este
marginita superior, iar multimea ![]() este
marginita inferior.
este
marginita inferior.
O functie marginita ![]() se spune ca este
integrabila Riemann pe
se spune ca este
integrabila Riemann pe ![]() daca pentru orice
sir de diviziuni
daca pentru orice
sir de diviziuni ![]() cu norma
cu norma ![]() cand
cand ![]() sirurile sumelor
Darboux
sirurile sumelor
Darboux ![]() si
si ![]() au o limita
comuna finita I, si se
noteaza
au o limita
comuna finita I, si se
noteaza
![]()
Tinand seama de definitia multimilor masurabile,
urmeaza ca definitia de mai sus este echi-valenta cu ![]() unde D
este multimea tuturor diviziunilor intervalului
unde D
este multimea tuturor diviziunilor intervalului ![]()
De obicei se noteaza 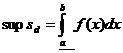
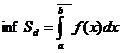 si se numesc, respectiv, integrala
inferioara Darboux si integrala superioara Darboux.
si se numesc, respectiv, integrala
inferioara Darboux si integrala superioara Darboux.
Criteriul lui Darboux. O functie ![]() ,
marginita, este integrabila pe
,
marginita, este integrabila pe ![]() daca pentru orice numar
daca pentru orice numar ![]() exista un numar
exista un numar ![]() astfel incat pentru orice diviziune d cu
astfel incat pentru orice diviziune d cu ![]() sa avem
sa avem ![]()
Conditia
este necesara. Sa presupunem ca f este integrabila. Fie ![]() un sir de diviziuni, astfel incat
un sir de diviziuni, astfel incat ![]() si
si ![]() cu
cu ![]()
Deoarece f este integrabila, pentru orice numar ![]() exista un
numar
exista un
numar ![]() astfel incat pentru
astfel incat pentru ![]() avem
avem ![]() ,
, ![]() , deci
, deci ![]()
Conditia
este suficienta. Fie ![]() un sir de
diviziuni (arbitrar) pentru care
un sir de
diviziuni (arbitrar) pentru care ![]() cand
cand ![]() Exista
Exista ![]() astfel incat pentru
orice
astfel incat pentru
orice ![]() avem
avem ![]() Din neegali-tatile
Din neegali-tatile
![]() unde am pus
unde am pus ![]() ,
, ![]() , rezulta ca
, rezulta ca ![]() si cum
si cum ![]() este oarecare, iar
sirul
este oarecare, iar
sirul ![]() este arbitrar,
urmeaza ca
este arbitrar,
urmeaza ca ![]() deci f este integrabila Riemann.
deci f este integrabila Riemann.
Daca
![]() este o suma
Riemann oarecare, relativa la diviziunea
este o suma
Riemann oarecare, relativa la diviziunea ![]() , avem
, avem ![]() iar daca f este integrabila, rezulta
ca
iar daca f este integrabila, rezulta
ca ![]() adica si
sumele Riemann sunt conver-gente catre o limita comuna care este
aria marginita de arcul de curba
adica si
sumele Riemann sunt conver-gente catre o limita comuna care este
aria marginita de arcul de curba ![]() ,
, ![]() Reciproca acestui
rezultat este de asemenea adevarata, astfel incat avem urma-toarea
definitie echivalenta a integrabilitatii.
Reciproca acestui
rezultat este de asemenea adevarata, astfel incat avem urma-toarea
definitie echivalenta a integrabilitatii.
Spunem
ca o functie ![]() definita pe
intervalul
definita pe
intervalul ![]() este integrabila
Riemann pe
este integrabila
Riemann pe ![]() daca pentru orice
sir de diviziuni
daca pentru orice
sir de diviziuni ![]() cu norma
cu norma ![]() cand
cand ![]() si pentru orice
alegere a punctelor intermediare
si pentru orice
alegere a punctelor intermediare ![]() sirurile Riemann
corespunzatoare
sirurile Riemann
corespunzatoare ![]() au o limita
comuna, finita I.
au o limita
comuna, finita I.
O functie marginita nu este neaparat integrabila Riemann.
Daca am dovedit ca o
functie f este integrabila
Riemann pe un interval ![]() , pentru cal-culul
efectiv al numarului I este
suficient sa luam un sir particular de diviziuni
, pentru cal-culul
efectiv al numarului I este
suficient sa luam un sir particular de diviziuni ![]() cu
cu ![]() cand
cand ![]() , precum si
un sir particular de puncte intermediare in fiecare diviziune.
, precum si
un sir particular de puncte intermediare in fiecare diviziune.
Functiile continue pe un interval ![]() sunt integrabile pe
sunt integrabile pe ![]()
Fie f
o functie continua pe ![]() . Functia f
este marginita pe
. Functia f
este marginita pe ![]() , deci
, deci 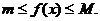
Fie d o diviziune a intervalului ![]() si
si ![]() un subinterval al lui d; avem
un subinterval al lui d; avem ![]()
![]() . Exista
doua puncte
. Exista
doua puncte ![]()
![]() pentru care
pentru care ![]()
![]()
Sa consideram sumele lui Darboux relative la diviziunea d
![]()
![]()
![]()
O functie continua intr-un interval inchis este si uniform
continua, deci pentru orice numar ![]() exista un numar
exista un numar ![]() astfel incat pentru orice pereche de puncte
astfel incat pentru orice pereche de puncte ![]()
![]() situata in intervalul
situata in intervalul ![]() sa avem
sa avem ![]() daca
daca 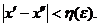
Sa alegem diviziunea d
astfel incat ![]() in aceasta situatie
in aceasta situatie
![]()
![]()
deci
![]()
ceea ce dovedeste ca f este integrabila.
Functiile monotone pe un interval ![]() sunt integrabile pe
sunt integrabile pe ![]()
Presupunem ![]() crescatoare pe
crescatoare pe ![]() ; daca d este o diviziune a intervalului
; daca d este o diviziune a intervalului ![]() , avem pentru un subinterval oarecare
, avem pentru un subinterval oarecare ![]()
![]()
![]() ,
,
deci
![]() ,
, ![]()
si
![]() ,
,
![]() ,
,
![]() .
.
Pentru ![]() , oarecare,
sa alegem diviziunea d astfel
incat
, oarecare,
sa alegem diviziunea d astfel
incat
![]()
deoarece
![]() ,
,
rezulta ca
![]()
si teorema este demonstrata.
Functiile monotone nu sunt neaparat continue. Am aratat ca functiile pot admite o infini-tate numarabila de discontinuitati de prima speta. Rezulta de aici: clasa functiilor integra-bile este mai cuprinzatoare decat clasa functiilor continue.
Deoarece un segment de dreapta este o multime
de arie nula, urmeaza ca daca schimbam valoarea unei
functii integrabile f intr-un
numar finit de puncte, functia f
rezultata este de asemenea integrabila, deci o functie
marginita pe ![]() , continua pe
, continua pe ![]() cu exceptia unui
numar finit de puncte, este integrabila pe
cu exceptia unui
numar finit de puncte, este integrabila pe ![]() .
.
Fie ![]() o functie
integrabila pe intervalul
o functie
integrabila pe intervalul ![]() . Integrala functiei
. Integrala functiei ![]() pe intervalul
pe intervalul ![]()
![]()
se numeste si integrala
definita a functiei ![]() pe intervalul
pe intervalul ![]() . Variabila x se
numeste variabila de integrare. Integrala definita este un
numar, deci nu depinde de variabila de integrare. Din aceasta cauza, variabila de
integrare se poate nota cu orice litera
. Variabila x se
numeste variabila de integrare. Integrala definita este un
numar, deci nu depinde de variabila de integrare. Din aceasta cauza, variabila de
integrare se poate nota cu orice litera
![]()
a) Daca
![]() se defineste prin
egalitatea
se defineste prin
egalitatea
![]() ,
,
de unde urmeaza imediat
![]()
b) Daca
![]() si este
integrabila pe
si este
integrabila pe ![]() , atunci
, atunci
![]() .
.
Intr-adevar,
daca ![]() pentru orice
pentru orice ![]() , rezulta ca pentru orice diviziune d avem
, rezulta ca pentru orice diviziune d avem ![]() ,
, ![]() , deci si
, deci si ![]() ,
, ![]() , de unde rezulta
, de unde rezulta ![]() .
.
c) Daca
f si g sunt integrabile pe ![]() , functia
, functia ![]() este integrabila
pe
este integrabila
pe ![]() si
si
![]()
(proprietatea de aditivitate a integralei fata de functii).
Fie d
o diviziune a intervalului ![]() si
si ![]() un punct oarecare al intervalului
un punct oarecare al intervalului ![]()
![]()
putem scrie deci
![]()
Fie acum un sir de diviziuni ![]() ale intervalului
ale intervalului ![]() cu
cu ![]() ; vom avea
; vom avea
![]()
si pentru ca f si g sunt integrabile,
![]() ,
, ![]() ,
,
de unde urmeaza ca f +g este integrabila
pe ![]() si
si
![]() .
.
Reciproca acestei proprietati
nu este in general adevarata, deci daca f+g este integrabila pe ![]() nu trebuie sa
deducem ca f si g sunt integrabile pe
nu trebuie sa
deducem ca f si g sunt integrabile pe ![]() .
.
d)
Daca
functia f este integrabila
pe ![]() , atunci
functia
, atunci
functia ![]() este integrabila pe
este integrabila pe ![]()
Intr-adevar avem
![]() ,
,
deci
![]()
si
pentru ca f este
integrabila pe ![]() urmeaza ca
urmeaza ca ![]() este integrabila
pe
este integrabila
pe ![]() si
si
![]() .
.
Din proprietatile (c) si (d)
rezulta ca daca f
si g sunt doua functii
integrabile pe ![]() , functia Af +
Bg, A, B fiind constante, este integrabila pe
, functia Af +
Bg, A, B fiind constante, este integrabila pe ![]() si
si
![]() .
.
Proprietatile (c) si (d) arata
ca multimea functiilor integrabile pe ![]() formeaza un
spatiu vectorial.
formeaza un
spatiu vectorial.
e) Daca
![]() pentru orice
pentru orice ![]() si daca f si g sunt
integrabile pe
si daca f si g sunt
integrabile pe ![]() , atunci
, atunci
![]()
(proprietatea de monotonie a integralei).
Functia ![]() este nenegativa
pe
este nenegativa
pe ![]() , deci conform proprietatii (b) avem
, deci conform proprietatii (b) avem
![]() sau
sau ![]() ;
;
aplicand proprietatea (c) rezulta ca
![]() .
.
f)
Daca f este
integrabila pe ![]() , atunci
oricare ar fi punctul
, atunci
oricare ar fi punctul ![]() avem
avem
![]() (1)
(1)
Daca ![]() , deci
, deci ![]() si relatia (1) este verificata.
In mod asemanator se arata ca relatia (1) este
adevarata daca
si relatia (1) este verificata.
In mod asemanator se arata ca relatia (1) este
adevarata daca ![]() Sa presupunem
Sa presupunem ![]() . Fie
. Fie ![]() un sir de diviziuni ale intervalului
un sir de diviziuni ale intervalului ![]() cu
cu ![]() . Daca
. Daca ![]() este un sir oarecare de sume Riemann
relativ la aceste diviziuni, atunci
este un sir oarecare de sume Riemann
relativ la aceste diviziuni, atunci
![]()
Fie ![]() un sir de
diviziuni ale intervalului
un sir de
diviziuni ale intervalului ![]() cu
cu ![]() Daca
Daca ![]() este un sir
oarecare de sume Riemann relativ la aceste diviziuni, avem
este un sir
oarecare de sume Riemann relativ la aceste diviziuni, avem
![]()
Daca
notam cu ![]() am obtinut un
sir de diviziuni ale intervalului
am obtinut un
sir de diviziuni ale intervalului ![]() cu
cu ![]() , deoarece
, deoarece ![]() .
.
Fie ![]() suma celor doua
sume Riemann
suma celor doua
sume Riemann ![]() si
si ![]() ; avem
; avem
![]() ,
, ![]() ;
;
la limita, egalitatea de mai sus ne conduce la
![]() .
.
Relatia obtinuta este
adevarata oricare ar fi succesiunea punctelor a, b, c. Intr-adevar, fie ![]() ; avem
; avem
![]()
insa
![]() ,
,
deci
![]()
sau
![]()
Din demonstratie rezulta si reciproca acestei proprietati, anume
g) Daca o functie f
este integrabila pe intervalele ![]() si
si ![]() , atunci f este integrabila pe
, atunci f este integrabila pe ![]() (proprietatea
de aditivitate a integralei fata de intervale).
(proprietatea
de aditivitate a integralei fata de intervale).
h) Daca
functia f este integrabila
pe intervalul ![]() , atunci f este
integrabila pe orice subinterval
, atunci f este
integrabila pe orice subinterval ![]() .
.
Fie ![]() , arbitrar si o diviziune d a intervalului
, arbitrar si o diviziune d a intervalului ![]() . Deoarece f este
integrabila, exista
. Deoarece f este
integrabila, exista ![]() astfel incat
astfel incat ![]() si
si ![]() .
.
Fie ![]() o diviziune a intervalului
o diviziune a intervalului ![]() cu
cu ![]() . Sa
completam diviziunea
. Sa
completam diviziunea ![]() a lui
a lui ![]() pana la o diviziune
pana la o diviziune ![]() a lui
a lui ![]() , astfel incat
, astfel incat ![]() , deci cu
, deci cu ![]() vom avea
vom avea
![]()
insa
![]()
deoarece ![]() si
si ![]() si din aceste
neegalitati rezulta
si din aceste
neegalitati rezulta
![]()
ceea ce dovedeste ca f este integrabila pe orice
interval ![]()
i)
Daca functia f este integrabila pe ![]() , atunci si
, atunci si ![]() este integrabila
pe
este integrabila
pe ![]() si
si
![]() .
.
Fie d
o diviziune a intervalului ![]() . Daca
notam cu
. Daca
notam cu ![]() , avem
, avem ![]()
![]()
![]() , iar daca
, iar daca ![]() este un subintervalui al lui
este un subintervalui al lui ![]() , avem
, avem ![]()
![]()
![]()
Avem mai multe cazuri de considerat:
a')
![]() In aceasta
situatie
In aceasta
situatie ![]() si
si ![]() .
.
b')
![]() Atunci
Atunci ![]() , deci
, deci ![]() .
.
c') ![]() Atunci
Atunci ![]()
![]() , deci in toate
cazurile
, deci in toate
cazurile ![]() putem scrie
putem scrie
![]()
sau
![]()
si pentru ca f este integrabila rezulta din aceasta neegalitate ca f este integrabila. Din
![]() ,
,
aplicand proprietatea (e) rezulta
![]()
deci
![]()
Toate aceste proprietati sunt folosite des in aplicatii.
Daca f este marginita
si integrabila pe intervalul ![]() , am vazut
ca avem
, am vazut
ca avem
![]() (1)
(1)
unde m si M sunt marginile funcsiei f in ![]() . Din (1)
urmeaza ca exista un numar
. Din (1)
urmeaza ca exista un numar ![]() cuprins intre m si M astfel incat
cuprins intre m si M astfel incat
![]()
Sa presupunem ca ![]() este si continua pe
este si continua pe ![]() ; in aceasta
situatie exista cel putin un punct
; in aceasta
situatie exista cel putin un punct ![]() astfel incat
astfel incat
![]()
deci
![]()
care se numeste formula mediei pentru integrale. Aceasta
formula are o interpretare geometrica simpla, si anume
spune ca exista cel putin un punct ![]() astfel incat aria marginita de arcul
de curba AB,
astfel incat aria marginita de arcul
de curba AB, ![]() si de segmentele ab, aA,bB (fig. 10)
este egala cu aria dreptunghiului de inaltime
si de segmentele ab, aA,bB (fig. 10)
este egala cu aria dreptunghiului de inaltime ![]() si baza b-a.
si baza b-a.
Un rezultat mai general este continut in urmatoarea teorema.
Daca f si p sunt doua functii
marginite si integrabile pe ![]() si daca
si daca
a) ![]() ,
, ![]() ;
;
b) ![]() este continua pe
este continua pe ![]()
atunci exista un punct ![]() astfel incat
astfel incat
![]() .
.
Sa presupunem mai intai pe ![]() numai
marginita si integrabila. Avem
numai
marginita si integrabila. Avem ![]() si pentru ca
si pentru ca
![]() urmeaza
urmeaza ![]() deci si
deci si
![]() ,
,
neegalitatea care arata ca exista un numar ![]() cuprins intre m si M astfel incat
cuprins intre m si M astfel incat
![]() (2)
(2)
Sa presupunem acum ca ![]() este si continua in
este si continua in ![]() , deci ca
exista un punct
, deci ca
exista un punct ![]() astfel incat
astfel incat ![]() ; in aceasta
situatie relatia (2) se scrie
; in aceasta
situatie relatia (2) se scrie
![]() .
.
Formula obtinuta se numeste formula generala a mediei pentru integrale.
Pentru ![]() obtinem formula
mediei.
obtinem formula
mediei.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2193
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved