| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
LINII IMPORTANTE IN TRIUNGHI
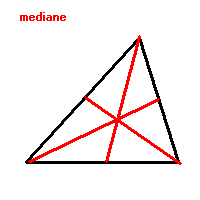
MEDIANA este segmentul care uneste un varf al triunghiului cu mijlocul laturii opuse.
-Medianele unui triunghi sunt concurente in centrul de greutate al triunghiului.
-Centrul de greutate se afla pe fiecare mediana la 2/3 de varf si 1/3 de baza, adica daca AA' este mediana in trABC si G este centrul de greutate, atunci AG=(2/3)AA'siGA'=(1/3)AA'.
-Mediana imparte un triunghi in doua triunghiuri cu aceeasi arie (echivalente).
-Centrul de greutate al unui triunghi formeaza cu vafurile triunghiului 3 triunghiuri echivalente si este singurul punct (din planul triunghiului) care are aceasta proprietate,
Intr-un triunghi dreptunghic, mediana corespunzatoare ipotenuzei este 1/2 din ipotenuza. Daca o mediana a unui triunghi este 1/2 din latura corespunzatoare ei, atunci triunghiul este dreptunghic.
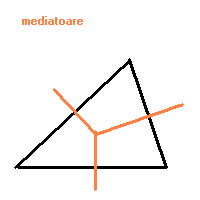
MEDIATOAREA (unui segment) este dreapta perpendiculara pe segment dusa prin mijocul segmentului.
-Mediatoarele laturilor unui triunghi sunt concurente; punctul lor de intersectie este centrul cercului cicumscris triunghiului (cercul care trece prin varfurile triunghiului).
-Orice punct de pe mediatoarea unui segment este egal departat de capetele segmentului; daca un punct este egal departat de doua puncte date, atunci el se afla pe mediatoarea segmentului determinat de cele doua puncte.
-Centrul cercului circumscris unui triunghi dreptunghic se afla la mijocul ipotenuzei. Raza acestui cerc este 1/2 din ipotenuza.
-Raza cercului circumscris unui triunghi oarecare este ![]() ,
unde a, b, c sunt lungimile laturilor si S este
aria.
,
unde a, b, c sunt lungimile laturilor si S este
aria.
-Raza cercului circumscris unui
triunghi echialteral de latura a este ![]() .
.
-Intr-un tr echilateral, si numai in tr echilateral, mediatoarele laturilor sunt inaltimi, mediane si bisectoare.
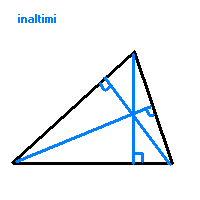
INALTIMEA este perpendi-culara dusa dintr-un varf al triunghiului pe latura opusa.
-Inaltimile unui tr. sunt concurente; punctul lor de intersectie se numeste ortocentrul triunghiului. Daca H este ortocentrul trABC, atunci A este ortocentrul trHBC, etc. Daca AA', BB' sunt inaltimi in trABC si H este intersectia lor, atunci CH AB.
-Inaltimea coresp. ipotenuzei unui tr dreptunghic este media geometrica a proiectiilor catetelor pe ipotenuza ( t. inaltimii).
-Inaltimea coresp. ipotenuzei unui tr dreptunghic este egala cu raportul dintre produsul catetelor si ipotenuza: h=(c1c2)/h.
-Inaltimea
unui triunghi echilateral de latua a este ![]() .
.
-Daca un triunghi are doua inaltimi congruente, atunci este isoscel.
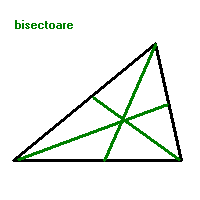
BISECTOAREA (unui unghi) este semidreapta cu originea in varful unghiului, care imparte unghiul in doua unghiuri congruente.
-Bisectoarele unui triunghi sunt concurente; punctul lor de intersectie este centrul cercului inscris in triunghi. Cercul inscris intr-un triunghi este cercul care are centrul in interiorul triunghiului si este tangent laturilor triunghiului.
-Intr-un triunghi bisectoarea oricarui unghi imparte latura opusa unghiului in segmente proportionale cu laturile unghiului. (t. bisectoarei)
-Orice punct de pe bisectoarea unui unghi este egal departat de laturile unghiului; daca un punct din interiorul unui unghi este egal departat de laturile unghiului ,atunci el se afla pe bisectoarea unghiului.
-Raza cercului inscris intr-un triunghi este egala cu S/p, unde S este aria triunghiului si p este semiperimetrul triunghiului.
-Bisectoarea exterioara a unui unghi este bisectoarea suplementului sau. Bisectoarea exterioara este perpendiculara pe bisectoarea interioara.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3517
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved