| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
MULTIMEA NUMERELOR COMPLEXE
x == - multimea numerelor complexe;
z=(x, y) - numar complex;
(x, 0)=x;
(0, 1)=i unitate imaginara;
(x, y)=(x, 0)+(0, y)= (x, 0)+(y, 0)(0, 1);
z1+z2=(x1, y1)+(x2, y2)=(x1+x2, y1+y2) adunarea;
z1z2=(x1, y1)(x2, y2)=(x1x2-y1y2, x1y2+x2y1) inmultirea.
Proprietati:
(z1+z2)+z3=z2+(z1+z3), z1,z2,z3I asociativitatea adunarii;
(z1z2)z3=z2(z1z3), z1,z2,z3I asociativitatea inmultirii;
z1+z2=z2+z1, z1,z2I comutativitatea adunarii;
z1z2=z2z1, z1,z2I comutativitatea inmultirii;
z+0=0+z=z, zI 0 element neutru pentru adunare;
z1=1z=z, zI 1 element neutru pentru inmultire;
z+(-z)=(-z)+z=0, zI (-z) element opus pentru z;
zz-1=z-1z=1, zI z-1 element invers pentru z;
z1(z2+z3)=z1z2+z1z3, z1,z2,z3I distributivitatea inmultirii fata de adunare;
(z1+z2)z3=z1z3+z2z3, z1,z2,z3I distributivitatea inmultirii fata de adunare.
Re(z)= x partea reala;
Im(z)=y coeficientul partii imaginare;
iy parte imaginara;
i unitate imaginara;
i2=-1;
z1+z2=(x1+i y1)+(x2+iy2)=(x1+x2)+i(y1+y2) adunarea;
z1z2=(x1+iy1)(x2+iy2)=(x1x2-y1y2)+i(x1y2+x2y1) inmultirea.
|
Egalitatea a doua numere complexe: z1=(x1+i y1)= (x1,y1), z2=(x2+iy2)= (x2,y2), z1=z2 x1=x2 si y1=y2; Conjugatul numarului complex z: |
Modulul unui numar complex |z|=|x+iy|= |z1z2|=|z1||z2|; Puterile lui i: |
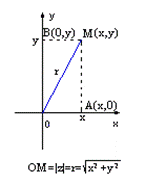Reprezentarea geometrica a numerelor complexe:
z=x+iy=(x,y), x,yI i se asociaza punctul M(x,y);
M se numeste imaginea geometrica a numarului complex x+iy;
x+iy se numeste afixul punctului M;
ΔAOM 
OM=
.
Forma trigonometrica a numerelor complexe: z=r(cos t* + i sin t*)
OM=
- r raza polara a imaginii lui z;
x=r cos t*, y=r sin t*,
tg t*=
; arg z=t* argument redus al lui z;
Arg z== argumentul lui z;
z1=r1(cos t1 + i sin t1), z2=r2(cos t2 + i sin t2) z1 z2=r1 r2 [cos(t1+ t2) + i sin (t1+ t2)] - inmultirea;
z=r(cos t + i sin t) zn=rn (cos nt + i sin nt) - ridicarea la putere;
(cos t + i sin t)n = (cos nt + i sin nt) - formula lui Moivre;
z1=r1(cos
t1 + i sin t1), z2=r2(cos t2
+ i sin t2) 
[cos(t1- t2) + i sin (t1- t2)]
- impartirea;
zn=r(cos t*
+ i sin t*) ⇒
zk=
, kI- radacina de ordinul
n.
Rezolvarea ecuatiei de gradul II cu coeficienti reali: ax2+bx+c=0 a, b, cI|R, a D=b2-4ac,
cazul 
x1, x2 sunt radacini
complexe conjugate;
Ecuatii binome: zn+c=0, c I nI , n
se scrie numarul (-c) sub
forma trigonometrica zn=r(cos t+i sin t)⇒zk=
, kI
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 3512
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
;
;
;
;
.
.