| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Matrici asociate unui graf. Proprietati ale grafurilor
Matricea conexiunilor directe
Fie un graf ![]() cu
cu ![]() . Asociem acestui graf o
matrice patratica booleana C,
. Asociem acestui graf o
matrice patratica booleana C, ![]() , ale carei elemente
sunt:
, ale carei elemente
sunt:
![]()
Matricea C poarta numele de matricea arcelor, matricea conexiunilor directe sau matricea de adiacenta pentru graful G.
|
|
|
figura 5.1 |
Exemplu Pentru graful din fig. 1 de mai sus scriem matricea conexiunilor directe:
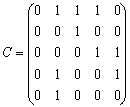
Observatii
Numarul de cifre 1 de pe linia i reprezinta numarul de
conexiuni directe ale lui ![]() , iar numarul de cifre 1
de pe coloana j reprezinta numarul conexiunilor directe cu
, iar numarul de cifre 1
de pe coloana j reprezinta numarul conexiunilor directe cu ![]()
Daca 2 grafuri au aceeasi matrice a conexiunilor directe (si aceeasi multime de varfuri) atunci cele 2 grafuri coincid.
Gradul exterior al varfului si se obtine adunand elementele de pe linia i a matricei C, iar gradul interior al aceluiasi varf se obtine adunand elementele de pe coloana i a matricei C.
Matricea drumurilor
Din matricea conexiunilor directe, prin anumite operatii se poate obtine o
matrice ![]() numita matricea drumurilor sau matricea
conexiunilor totale, in care
numita matricea drumurilor sau matricea
conexiunilor totale, in care
![]()
Definitie Puterea de atingere ![]() a varfului
a varfului ![]() in graful
in graful ![]() este egala cu numarul de varfuri la care se
poate ajunge din
este egala cu numarul de varfuri la care se
poate ajunge din ![]() , adica egala cu numarul
de elemente "1" de pe linia "i" din matricea D.
, adica egala cu numarul
de elemente "1" de pe linia "i" din matricea D.
Pentru elaborarea unui algoritm de determinare a matricii drumurilor introducem o operatie adecvata pe multimea formata din elementele 0 si 1, numita operatie de "adunare booleana" cu regulile urmatoare:
Astfel algoritmul de determinare al matricii drumurilor unui graf pornind de la matricea conexiunilor directe, este:
Pentru construirea liniei "i" din
matricea D ![]() urmarim elementele egale cu "1" de pe linia "i" din
matricea C: daca
urmarim elementele egale cu "1" de pe linia "i" din
matricea C: daca ![]()
![]()
![]() , ., atunci
, ., atunci ![]()
![]()
![]()
Folosind
adunarea booleana, se aduna liniile ![]() din matricea C la linia "i"; noile valori "1"
aparute se trec in linia "i" a matricei D; fie
din matricea C la linia "i"; noile valori "1"
aparute se trec in linia "i" a matricei D; fie ![]() pozitiile ocupate de aceste noi valori in
cadrul linie i.
pozitiile ocupate de aceste noi valori in
cadrul linie i.
Adunam (boolean) liniile ![]() din C la linia "i" trecand noile valori de "1"
aparute in linia "i" a matricii D.
din C la linia "i" trecand noile valori de "1"
aparute in linia "i" a matricii D.
Procesul se continua pana la aparitia uneia din situatiile:
a)
sau toate elementele ![]()
![]() devin egale cu "1".
devin egale cu "1".
b) nu mai apare nici un element egal cu "1", caz in care locurile ramase libere se completeaza cu zerouri si se trece la linia "i+1", pentru care se repeta procedeul.
Exemplu Pentru graful din fig.5 cu matricea conexiunilor directe C asociata, determinam matricea drumurilor D.
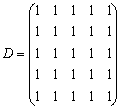
Observatii
Graful G are circuite, caci exista i astfel incat ![]() .
.
Avem puterile de atingere ale varfurilor
![]()
Determinarea drumurilor hamiltoniene
Teorema
(Y. Chen) Un graf fara circuite, care are
"n" varfuri, contine un drum hamiltonian, daca si numai daca avem: ![]()
Algoritmul inmultirii latine (A. Kaufmann 1963)
Fie o matrice ![]() , care in locul valorilor
de "1" utilizate in matricea obisnuita a arcelor, utilizeaza insusi arcul
respectiv, reprezentat prin varfurile care il compun, deci
, care in locul valorilor
de "1" utilizate in matricea obisnuita a arcelor, utilizeaza insusi arcul
respectiv, reprezentat prin varfurile care il compun, deci ![]() , unde
, unde ![]()
Prin suprimarea primei litere in
matricea ![]() se obtine o matrice
se obtine o matrice ![]() numita "matricea destinatiilor posibile". Se
compun matricele
numita "matricea destinatiilor posibile". Se
compun matricele ![]() si
si ![]() prin operatia de "inmultire latina",
prin operatia de "inmultire latina", ![]() definita astfel: inmultirea latina a
matricilor se face formal ca si inmultirea a 2 matrici, fara insumare si fara
inmultire efectiva tinand cont ca:
definita astfel: inmultirea latina a
matricilor se face formal ca si inmultirea a 2 matrici, fara insumare si fara
inmultire efectiva tinand cont ca:
- inmultirea latina a doua componente participante la calcul este nul daca cel putin una din ele este nula.
- inmultirea latina a doua componente participante este nul daca au varf comun.
- rezultatul compunerii consta in scrierea in continuare a varfurilor componente ale simbolurilor participante.
Prin repetarea inmultirii latine avem: ![]() ,
, ![]() , ., si
algoritmul continua pana la obtinerea matricii
, ., si
algoritmul continua pana la obtinerea matricii ![]() , deoarece
intr-un graf cu n varfuri un drum hamiltonian are
, deoarece
intr-un graf cu n varfuri un drum hamiltonian are ![]() arce. In matricea
arce. In matricea ![]() citim, conform modului de scriere de mai sus
toate drumurile hamiltoniene ale grafului. Daca toate elementele lui
citim, conform modului de scriere de mai sus
toate drumurile hamiltoniene ale grafului. Daca toate elementele lui ![]() sunt zerouri, (
sunt zerouri, (![]() ), graful
nu admite drum hamiltonian.
), graful
nu admite drum hamiltonian.
Exemplu Sa se determine drumurile hamiltoniene pentru graful din figura 5.1.
Solutie: Cum stim, graful are circuite. Vom folosi metoda
inmultirii latine. Matricele ![]() si
si ![]() sunt:
sunt:
 si
si 
Atunci:
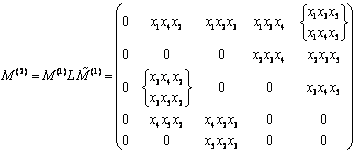
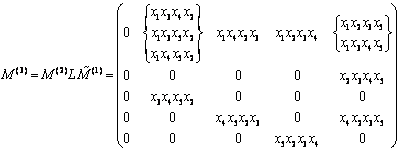

Astfel, in graful dat exista 4 drumuri hamiltoniene,
Algoritmul Bellman-Kalaba
Fie ![]() un graf, vom introduce o functie
un graf, vom introduce o functie ![]() ce asociaza fiecarui arc din o valoare reala. Notam:
ce asociaza fiecarui arc din o valoare reala. Notam: ![]() si
si ![]() graful valuat. In cazurile reale valuarea poate reprezenta:
graful valuat. In cazurile reale valuarea poate reprezenta:
- distanta dintre 2 puncte (localitati)
- timpi sau costuri intr-o retea de transport etc.
Pentru un drum ![]() in graful G vom numi "valoare a drumului",
suma valorilor arcelor componente, adica:
in graful G vom numi "valoare a drumului",
suma valorilor arcelor componente, adica: ![]()
Vrem sa determinam drumul "d" de la un varf oarecare ![]() la varful
la varful ![]() , pentru care valoarea
lui
, pentru care valoarea
lui ![]() sa fie minima. Pentru aceasta introducem "matricea
extinsa a valorilor arcelor"
sa fie minima. Pentru aceasta introducem "matricea
extinsa a valorilor arcelor" ![]() , data de
, data de

si notam cu ![]() valoarea minima a drumului d de la
valoarea minima a drumului d de la ![]() la
la ![]() in graful dat, considerat in multimea
drumurilor de cel mult k arce, cu
in graful dat, considerat in multimea
drumurilor de cel mult k arce, cu ![]() valoarea minima a drumului de la
valoarea minima a drumului de la ![]() la
la ![]() , considerata in multimea
tuturor drumurilor (indiferent de numarul de arce componente).
, considerata in multimea
tuturor drumurilor (indiferent de numarul de arce componente).
Algoritmul de construire a vectorilor ![]() se bazeaza pe urmatoarele propozitii:
se bazeaza pe urmatoarele propozitii:
Propozitia
1: Pentru orice ![]() avem
avem ![]()
Propozitia 2: Daca
exista ![]() pentru care
pentru care ![]() ,
pentru orice
,
pentru orice ![]() , atunci:
, atunci:
a)
![]()
![]() , pentru orice
, pentru orice ![]()
b)
![]()
![]()
Algoritmul de determinare a drumului minim este:
Etapa 1:
Se considera graful valuat ![]()
![]() Se construieste matricea
estinsa a valorilor arcelor
Se construieste matricea
estinsa a valorilor arcelor ![]()
Etapa 2: Se
adauga matricii V, liniile suplimentare ![]() astfel:
astfel:
a)
linia ![]() coincide cu transpusa coloanei n a matricii V,
coincide cu transpusa coloanei n a matricii V,
![]()
b)
presupunand completata linia ![]() , se completeaza linia
, se completeaza linia ![]() conform propozitiei 1.
conform propozitiei 1.
c)
se continua aplicarea punctului (b) pana la obtinerea a 2
linii ![]() si
si ![]() identice.
identice.
Etapa 3:
Se determina regresiv drumul minim de la ![]() la
la ![]() astfel:
astfel:
- se aduna linia "i" din V cu linia ![]() urmarindu-se rezulta-tul minim ce se poate
obtine. Sa presupunem ca:
urmarindu-se rezulta-tul minim ce se poate
obtine. Sa presupunem ca: ![]() , atunci primul arc din drumul minim de la
, atunci primul arc din drumul minim de la ![]() la
la ![]() este arcul
este arcul ![]()
- se aduna linia "j" din V cu ![]() retinand valoare minima, aflata de exemplu pe
coloana "t", atunci al doilea arc va fi
retinand valoare minima, aflata de exemplu pe
coloana "t", atunci al doilea arc va fi ![]() , s.a.m.d. Ultimul
succesor determinat va fi
, s.a.m.d. Ultimul
succesor determinat va fi ![]()
Algoritmul de determinare a drumului maxim
Etapa 1:
Se construieste matricea V a valorilor arcelor 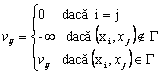
Etapa 2:
Similar cu etapa 2 din algoritmul
anterior, dar la
b) linia ![]()
![]() se completeaza prin relatia
se completeaza prin relatia ![]()
Etapa 3: Determinarea drumului maxim se determina la fel ca la etapa 3 anterioara.
Vom prezenta doua exemple de determinare a drumului minim, respectiv maxim cu ajutorul algoritmului Bellman-Kalaba.
Exemplu Varfurile ![]() reprezinta intreprinderi, iar pe arce este
marcata durata executarii controlului in punctul
reprezinta intreprinderi, iar pe arce este
marcata durata executarii controlului in punctul ![]() dupa efectuarea lui in punctul
dupa efectuarea lui in punctul ![]() in unitatea de timp corespunzatoare. Sa se
determine timpul minim de control, dintre
in unitatea de timp corespunzatoare. Sa se
determine timpul minim de control, dintre ![]() si
si ![]()
|
|
|
figura 5.2 |
Solutie: Construim matricea V a valorilor arcelor, si folosind algoritmul de determinare a drumului minim vom intocmi tabelul:
|
|
|
|
|
|
|
|
|
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
| |||||||
|
|
Drumul minim de la ![]() la
la ![]() va fi
va fi ![]() cu
cu ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4333
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved