| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
NUMERE NATURALE
RIDICAREA LA PUTERE(EXPONENT NUMAR NATURAL)
Ridicarea la putere este o inmultire repetata.
Exemplu: ![]() ; se numeste baza iar este exponent.
; se numeste baza iar este exponent.
Daca avem in general baza a si exponentul n, puterea a n-a a numarului a este produsul a n factori egali cu numarul a.
![]() cu
a si n numere naturale
cu
a si n numere naturale
Observatii
![]()
2. ![]()
3.![]()
![]()
4. ![]()
Exponentul arata de cate ori se repeta baza in produsul prin care se calculeaza puterea.
Ridicarea la putere este o operatie de ordinul al treilea, adica in lipsa parantezelor, se efectueaza inaintea celorlalte operatii.
Puterea a 2-a a unui numar natural de m cifre are 2m-1 cifre sau 2m cifre.
Orice putere a unui numar
natural care are ultima cifra 0, 1, 5 sau 6 va avea ultima cifra tot 0, 1, 5,
6. Vom scrie de exemplu ![]() .Prin u(n) se intelege ultima cifra
a numarului n
.Prin u(n) se intelege ultima cifra
a numarului n
Orice putere a unui numar care are ultima cifra 4, are ultima cifra 6 daca exponentul este par si 4 daca exponentul este impar
Exercitiu.
.Oricare ar fi numarul natural k, avem:
![]() are ultima cifra 6;
are ultima cifra 6;
![]() are ultima cifra 2;
are ultima cifra 2;
![]() are ultima cifra 4;
are ultima cifra 4;
![]() are ultima cifra 8; cu k
are ultima cifra 8; cu k![]() 0
0
.Sa se stabileasca ultima cifra a puterilor numerelor 3, 7, 8, 9.
Reguli de calcul cu puteri
i ![]()
ii) ![]()
iii) ![]() cu
m>n
cu
m>n
iv) ![]()
Patrate perfecte
Puterea a 2-a a unui numar natural se mai numeste si patratul acelui
numar. Exemplu: ![]() se citeste"6 la puterea a doua" sau
la patrat".
se citeste"6 la puterea a doua" sau
la patrat".
Numarul natural care este patratul altui numar natural se numeste patrat perfect.Exemple: 4 etc.
![]() este patrat perfect, oricare ar fi a
si k numere naturale,
este patrat perfect, oricare ar fi a
si k numere naturale, ![]() .
.
Patratul oricarui numar natural se poate termina cu una din cifrele 0, 1, 4, 5, 6, 9. Nu intotdeauna numerele care se termina in aceste cifre sunt patrate perfecte. De exemplu: 11; 14; 39 etc.
Un numar care se termina in una din cifrele 2, 3, 7, sau 8 nu este patrat perfect.
Pentru a arata ca un numar nu este patrat perfect mai putem arata ca el este
cuprins intre doua patrate de numere consecutive. De exemplu: 75 nu este patrat perfect, pentru ca ![]()
Exercitii
Sa se completeze tabelul:
|
x |
|
|
|
|
|
|
.Sa se completeze tabelul:
|
x |
|
|
|
|
|
| ||||
Compararea puterilor.
1.Puteri cu aceeasi baza.
Fie a, m, n numere
naturale nenule, ![]() .
.
Daca
m<n, atunci![]() .
.
Exemplu: ![]() (25<625)
(25<625)
|
n | |||||||
|
| |||||||
|
|
2.Puteri cu acelasi exponent
Fie a,b,n, numere naturale nenule. Daca a<b,
atunci ![]() .Se poate vedea din tabelul de mai sus acest lucru.
.Se poate vedea din tabelul de mai sus acest lucru.
3.Puteri cu baze diferite si exponenti diferiti.
Pentru a compara doua puteri cu baze diferite si exponenti diferiti, se aduc puterile, daca se poate, fie la aceeasi baza, fie la acelasi exponent.
Exemplu: ![]() ;
; ![]()
![]()
Dar ![]()
Exercitii.
Sa se compare numerele din tabel:
|
a |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
Sa se arate ca:
a) ![]()
b) ![]()
Sa se scrie in ordine crescatoare numerele: ![]()
Sa se scrie folosind o singura putere numarul:
a) ![]()
b) ![]()
c) ![]()
Sa se calculeze: 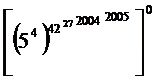
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4515
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved