| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
NUMERE REALE
CLASA a VII-a
Lectia 1
Radacina patrata.
Profesor V Corcalciuc Scoala nr. 146 I G Duca Bucuresti
(Lectii facute conform programei pentru clasa a VI I-a )
Radacina patrata a unui numar rational pozitiv.
|
x |
|
|
||||
|
|
|
|
Observam ca patratul unui numar rational este un numar pozitiv.
Patratul unui numar natural este patrat perfect daca este patratul unui numar intreg.
Definitie.Numarul rational ![]() se numeste radacina patrata a numarului a daca
se numeste radacina patrata a numarului a daca
![]()
Se scrie ![]()
Semnul 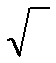 se numeste radical . In cazul radacinii patrate acesta este radical de
ordinul 2 Mai exista si radicali de ordin superior
lui 2.)
se numeste radical . In cazul radacinii patrate acesta este radical de
ordinul 2 Mai exista si radicali de ordin superior
lui 2.)
Exemple.

EXTRAGEREA RADACINII PATRATE DINTR-UN NUMAR NATURAL PATRAT PERFECT.
Pentru a calcula radacina patrata avem mai multe metode.
Descompunem numarul in factori primi si scriem numarul ca
putere( de 2 sau multiplii de 2). Baza puterii este radacina patrata.
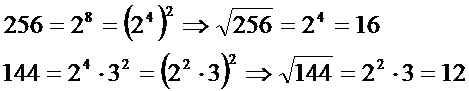
![]()
Avem un algoritm de extragere a radacinii patrate.
![]() ...se desparte numarul in grupe de cate doua cifre de la
dreapta
...se desparte numarul in grupe de cate doua cifre de la
dreapta
la stanga.
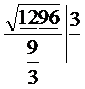 ..Cautam numarul cel mai mare al carui patrat este foarte
..Cautam numarul cel mai mare al carui patrat este foarte
apropiat de 12.
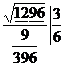 ...Langa primul rest 3 coboram grupa a doua 96 si dublam
...Langa primul rest 3 coboram grupa a doua 96 si dublam
primul cat 3.
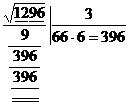 ..Vedem de cate ori se cuprinde 6 in 39 (
de 6 ori) si-l adaugam langa numarul dublat, apoi inmultim cu el. Ned a
restul 0 la scadere si deci am obtinut
..Vedem de cate ori se cuprinde 6 in 39 (
de 6 ori) si-l adaugam langa numarul dublat, apoi inmultim cu el. Ned a
restul 0 la scadere si deci am obtinut ![]()
Exercitii.
Sa se extraga radacina patrata din urmatoarele numere
EXTRAGEREA RADACINII PATRATE DINTR-UN NUMAR RATIONAL SCRIS SUB FORMA DE FRACTIE ORDINARA.
Daca avem fractia ireductibila
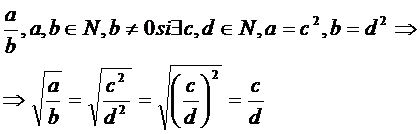
 Exemple.
Exemple.
EXTRAGEREA RADACINII PATRATE DINTR-UN NUMAR RATIONAL SCRIS SUB FORMA DE FRACTIE ZECIMALA.
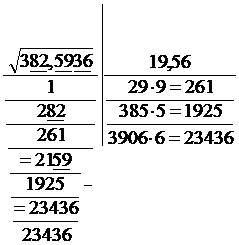
Se desparte numarul de la virgula
spre stanga si de la virgula spre
dreapta in grupe de cate doua cifre.
Se aplica acelasi procedeu ca la numerele fara virgula.
Se poate intampla san u putem face grupe de cate doua cifre de la virgula spre dreapta si in acest caz se completeaza cu cifra 0.
Daca numarul rational din care extragem radacina patrat nu este patrat perfect, de obicei se extrag doua zecimale dupa virgula.
Exercitii. Sa se extraga radacina patrata din urmatoarele numere:
6); 126,8; 0,4; 124,523; 46,8; 34,6; 24,008
APROXIMARI
Numerele invatate pana acum
sunt numerele rationale, adica numerele care se pot scrie sub forma 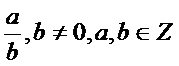
Exista si numere care nu se
pot scrie sub forma de mai sus si anume fractiile zecimale infinite
neperiodice. Sa luam de exemplu ![]() sau
sau ![]() Aceste numere nu sunt rationale ,
caci nu se pot scrie sub forma
Aceste numere nu sunt rationale ,
caci nu se pot scrie sub forma ![]() si ele formeaza
multimea numerelor IRATIONALE, notata cu I
si ele formeaza
multimea numerelor IRATIONALE, notata cu I
In calcule fiindca nu putem scrie valoarea exacta a lor, le aproximam, adica le scriem sub forma de fractie zecimala cu una, doua sau mai multe zecimale.
De exemplu: ![]()
Aceste aproximari pot fi prin lipsa sau prin adaos.
|
|
Prin lipsa |
Prin adaos. |
|
Aproximatie de o zecime | ||
|
Aproximatie de o sutime | ||
|
Aproximatie de o miime | ||
|
Aproximatie de o unitate | ||
|
| ||
|
Aproximatie de o zecime | ||
|
Aproximatie de o sutime | ||
|
Aproximatie de o miime | ||
|
Aproximatie de o unitate |
Numerele irationale pot fi approximate si prin rotunjire.
![]() Rotunjire la prima zecimala 2,6
Rotunjire la prima zecimala 2,6
Rotunjire la a doua zecimala 2
Rotunjire la a treia zecimala 2,646
Ultima zecimala la care se face rotunjirea ramane neschimbata daca dupa ea urmeaza 0,1,2,3,4.
Ultima zecimala la care se face rotunjirea se mareste cu 1 daca dupa ea urmeaza 5,6,7,8,9.
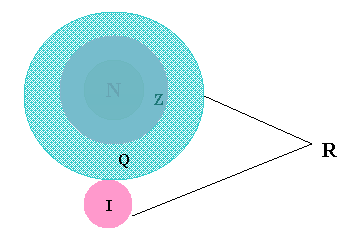
In concluzie putem face o schema cu multimele de numere invatate pana acum.

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5950
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved