| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Preliminarii asupra functiilor convexe de o variabila reala
Fie ![]() Aplicatia
Aplicatia
![]() (1)
(1)
este un
omeomorfism al lui [0,1] pe ![]() .Deci orice
punct
.Deci orice
punct ![]() se reprezinta in mod unic sub forma
se reprezinta in mod unic sub forma ![]() ,cu
,cu ![]() .
.
Definitie 1
Fie H o parte a
lui R,![]() .Se numeste
grafic(sau multime reprezentativa ) a functiei f,si se noteaza
.Se numeste
grafic(sau multime reprezentativa ) a functiei f,si se noteaza ![]() urmatoarea multime de puncte din
urmatoarea multime de puncte din ![]() :
:
![]() (2)
(2)
Definitie 2
Fie H o parte a
lui R, ![]() .Se spune
ca punctul
.Se spune
ca punctul ![]() din
din ![]() se afla deasupra(respectiv strict deasupra)
graficului functiei f daca
se afla deasupra(respectiv strict deasupra)
graficului functiei f daca ![]() si
si ![]()
(respectiv ![]() ).
).
O definitie
corespunzatoare pentru punctele ![]() din
din ![]() care se afla sub(respectiv strict sub)
graficul functiei
care se afla sub(respectiv strict sub)
graficul functiei ![]() daca
daca ![]() si
si ![]() (respectiv
(respectiv ![]() ).
).
Lema 1
Fie ![]() si
si ![]() doua puncte din
doua puncte din ![]() astfel incat
astfel incat ![]() Fie
Fie 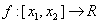 urmatoarea aplicatie liniara:
urmatoarea aplicatie liniara:
![]() (3)
(3)
Atunci graficul
functiei f este urmatoarea multime de puncte din ![]()
![]()
Demonstratie
Conform definitiei 1,graficul functiei f definite de (3) este:
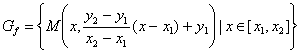 (5)
(5)
Tinand seama insa
ca orice punct ![]() se reprezinta in mod unic sub forma
se reprezinta in mod unic sub forma
![]() ,
,
si ca aplicatia
![]() ,
,
este un
omeomorfism al lui ![]() pe
pe ![]() ,din (5)
rezulta (4).
,din (5)
rezulta (4).
Observatie
Este usor de
vazut ca,geometric,graficul functiei f definita de (3) reprezinta multimea
punctelor din plan situate pe segmentul inchis ce uneste punctele ![]() si
si ![]() .Tinand
seama de aceasta observatie ,rezulta ca (4) este reprezentarea parametrica a segmentului inchis ce uneste
punctele
.Tinand
seama de aceasta observatie ,rezulta ca (4) este reprezentarea parametrica a segmentului inchis ce uneste
punctele ![]() si
si ![]()
Definitie 3
Fie ![]() un interval al dreptei reale si fie
un interval al dreptei reale si fie ![]() o functie numerica finita.Functia f se numeste
convexa in I daca pentru orice doua puncte
o functie numerica finita.Functia f se numeste
convexa in I daca pentru orice doua puncte ![]()
![]() si orice
si orice ![]() are loc relatia:
are loc relatia:
![]()
In cele ce
urmeaza vom da o interpretare geometrica definitiei 3.Fie punctele ![]() si
si 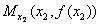 .Conform
lemei 1, multimea punctelor din plan situate pe segmentul inchis
.Conform
lemei 1, multimea punctelor din plan situate pe segmentul inchis ![]() se scrie astfel(vezi (2)):
se scrie astfel(vezi (2)):
![]() (7)
(7)
Sa consideram pe
de alta parte restrictia lui f la segmentul ![]() .Graficul
acestei restrictii este:
.Graficul
acestei restrictii este:
![]() (8)
(8)
Comparand (6),(7),(8),putem reformula definitia 3 astfel:
Definitie 4
Se spune ca
functia numerica finita f,definita intr-un interval ![]() ,este
convexa in I,daca pentru orice doua puncte
,este
convexa in I,daca pentru orice doua puncte ![]() ,orice
punct
,orice
punct ![]() cu
cu ![]() al graficului functiei f se afla sub segmentul
al graficului functiei f se afla sub segmentul
![]() .
.
Definitie 5:
Se spune ca o functie numerica f,definita intr-un interval ![]() ,este strict convexa
,este strict convexa
in I ,daca pentru orice doua puncte ![]() si
orice
si
orice ![]() astfel incat
astfel incat ![]()
![]() (9)
(9)
Evident,cu aceleasi argumente folosite pentru a obtine varianta geometrica a definitiei 3 sub forma definitiei 4,definitia 5 poate fi reformulata astfel:
Definitie 6
Se spune ca
functia numerica finita f,definita intr-un interval ![]() ,este
convexa in I,daca pentru orice doua puncte
,este
convexa in I,daca pentru orice doua puncte ![]() ,orice
punct
,orice
punct ![]() al graficului lui f cu
al graficului lui f cu ![]() se afla strict sub segmentul
se afla strict sub segmentul ![]() (sau,ceea
ce este acelasi lucru,orice punct al segmentului
(sau,ceea
ce este acelasi lucru,orice punct al segmentului ![]() diferit de extremitati se afla strict deasupra
graficului lui f ).
diferit de extremitati se afla strict deasupra
graficului lui f ).
Propozitie 1:
Daca f este continua
pe ![]() ,atunci definitia 3 este echivalenta cu urmatoarea:
,atunci definitia 3 este echivalenta cu urmatoarea:
f este convexa pe ![]() daca pentru orice doua puncte
daca pentru orice doua puncte ![]() :
:
![]() (10)
(10)
Demonstratie
Este usor de vazut ca una dintre implicatii este
imediata:daca (6) este adevarata pentru orice ![]() si orice
si orice ![]() ,atunci,pentru
,atunci,pentru
![]() din (6)
rezulta (10).Reciproc,vom dovedi ca daca f este continua in I si daca (10) este adevarata pentru orice
din (6)
rezulta (10).Reciproc,vom dovedi ca daca f este continua in I si daca (10) este adevarata pentru orice ![]() ,atunci (6)
este adevarata pentru orice
,atunci (6)
este adevarata pentru orice ![]() ,si orice
,si orice ![]() .Fie
.Fie ![]() astfel:
astfel:
![]() (11)
(11)
A dovedi ca (6) este
adevarata,pentru orice ![]() ,revine la
a dovedi ca
,revine la
a dovedi ca![]() :
:
![]()
Presupunem ca nu
este asa ,deci ca exista cel putin o valoare ![]() pentru care
pentru care ![]() Este
evident ca aplicatia
Este
evident ca aplicatia ![]() este continua pe
este continua pe ![]() .
.
Fie ![]() Avem
Avem ![]() ,deoarece
,deoarece ![]() Fie
Fie ![]() cea mai mica valoare a lui
cea mai mica valoare a lui ![]() din
din ![]() pentru care
pentru care ![]() este atins:
este atins:
![]()
Este clar ca ![]() deoarece
deoarece ![]() in timp ce
in timp ce ![]()
Asadar,![]() Exista deci
un
Exista deci
un ![]() astfel incat
astfel incat ![]() si astfel incat in intervalul
si astfel incat in intervalul 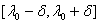 sa
nu se mai gaseasca nici un alt punct in afara de
sa
nu se mai gaseasca nici un alt punct in afara de ![]() care sa realizeze maximul lui
care sa realizeze maximul lui ![]() pe
pe ![]()
Scriind inegalitatea (10) pentru:
![]() ,rezulta
,rezulta
![]() ,
,
ceea ce contrazice faptul ca ![]() Asadar,negarea
proprietatii
Asadar,negarea
proprietatii ![]() conduce la contradictie.Rezulta ca
conduce la contradictie.Rezulta ca ![]() ,ceea ce
revine la (6).
,ceea ce
revine la (6).
In cele ce urmeaza,in afara unor cazuri ce vor fi mentionate special,functiile convexe sunt considerate conform definitiei 3.
Lema 2:
Fie f o functie numerica finita,definita intr-un interval ![]() si
fie
si
fie ![]() un punct interior al lui I.Daca f este
convexa(respectiv strict convexa) in I,atunci aplicatia:
un punct interior al lui I.Daca f este
convexa(respectiv strict convexa) in I,atunci aplicatia:
![]() (12)
(12)
este crescatoare(strict crescatoare).
Demonstratie:
Fie ![]() Va trebui
sa dovedim ca
Va trebui
sa dovedim ca ![]() (respectiv
(respectiv ![]() ) .Avem:
) .Avem:![]()
![]()
![]() (13)
(13)
Deoarece ![]() ,sunt
posibile numai urmatoarele trei cazuri:
,sunt
posibile numai urmatoarele trei cazuri:
1.![]() ;
;
2.![]()
3.![]()
Fie cazul 1 si fie f convexa.Atunci sunt adevarate urmatoarele:
a) exista
![]() unic,
unic,![]() astfel
incat
astfel
incat
![]() ;
;
b)![]()
Tinand seama de 1,a si b in (13) rezulta:
![]()
![]()
egalitatea cu zero fiind consecinta a faptului ca din a) rezulta :
![]()
Se intelege,daca f este strict convexa,atunci b) se scrie sub forma:
![]() ,
,
Si cu acelasi rationament ca mai sus,din 1.a,c rezulta :
![]()
Demonstratia corespunzatoare cazurilor 2 si 3 se face cu o tehnica analoaga.
Teorema 1:
Fie ![]() un interval al dreptei reale,
un interval al dreptei reale,![]() , o functie
numerica finita convexa in I,
, o functie
numerica finita convexa in I, ![]() un punct interior al lui I.Atunci exista
derivata la dreapta a lui f in punctul
un punct interior al lui I.Atunci exista
derivata la dreapta a lui f in punctul ![]() (
(![]() ),exista
derivata la stanga a lui f in punctul
),exista
derivata la stanga a lui f in punctul ![]() (
(![]() ) si:
) si:
![]() (14)
(14)
Demonstratie:
Conform lemei 2,aplicatia:
![]()
este crescatoare.Sa notam:
![]()
si consideram restrictia lui ![]() la
la ![]() ,pe care o
vom nota
,pe care o
vom nota ![]() .Aceasta
restrictie este evident crescatoare pe
.Aceasta
restrictie este evident crescatoare pe ![]() si,in plus,marginita inferior.Fie,intr-adevar,
si,in plus,marginita inferior.Fie,intr-adevar,![]() .Utilizand
lema 2,pentru orice
.Utilizand
lema 2,pentru orice ![]() avem:
avem:
![]() (15)
(15)
Din faptul ca ![]() este crescatoare si marginita inferior pe
este crescatoare si marginita inferior pe ![]() rezulta ca exista si este finita urmatoarea
limita:
rezulta ca exista si este finita urmatoarea
limita:
![]() (16)
(16)
cu alte cuvinte,![]() exista si
este finita.Pe de alta parte din (15) si (16) rezulta ca pentru orice
exista si
este finita.Pe de alta parte din (15) si (16) rezulta ca pentru orice ![]() :
:
![]() (17)
(17)
Aceasta inegalitate arata ca ![]() ,care este evident crescatoare,este marginita
superior si,deci exista si este finita urmatoarea limita:
,care este evident crescatoare,este marginita
superior si,deci exista si este finita urmatoarea limita:
![]() (18)
(18)
cu alte cuvinte,exista si este
finita ![]() Din (17) si
(18) rezulta (14).Teorema este demonstrata.
Din (17) si
(18) rezulta (14).Teorema este demonstrata.
Din teorema 1 rezulta imediat:
Corolar 1:
Fie ![]() un interval al dreptei reale,
un interval al dreptei reale, ![]() o functie numerica finita,convexa in I.Atunci
f este continua in orice punct interior al lui I.
o functie numerica finita,convexa in I.Atunci
f este continua in orice punct interior al lui I.
Demonstratie:
Fie ![]() un punct interior al lui I.Conform teoremei
1,exista
un punct interior al lui I.Conform teoremei
1,exista ![]() ,deci f
este continua la dreapta in punctul
,deci f
este continua la dreapta in punctul ![]() ,exista
,exista ![]() ,deci f
este continua si la stanga in
,deci f
este continua si la stanga in ![]() ,deci f
este continua in
,deci f
este continua in ![]() .
.
Corolar 2:
Fie I un interval al dreptei
numerice, f o functie numerica pe I convexa in I(respectiv strict convexa in
I),![]() si
si ![]() doua puncte interioare ale lui I astfel incat
doua puncte interioare ale lui I astfel incat ![]()
Atunci:
![]() , (19)
, (19)
respectiv:
![]() (20)
(20)
Demonstratie:
![]() Sa observam
ca
Sa observam
ca ![]() si
si ![]() exista,in conformitate cu teorema 1.Vom
analiza,mai intai,cazul f convexa.Deoarece
exista,in conformitate cu teorema 1.Vom
analiza,mai intai,cazul f convexa.Deoarece ![]() si
si ![]() sunt puncte interioare ale lui
sunt puncte interioare ale lui
I cu ![]() ,fie
,fie ![]()
Aplicatia ![]() fiind crescatoare (din lema 1) rezulta:
fiind crescatoare (din lema 1) rezulta:
![]() ,
,
de unde
![]()
![]() (21)
(21)
Analog,aplicatia ![]()
fiind crescatoare rezulta :
![]() ,
,
de unde
![]() (22)
(22)
Din (21) si (22) rezulta (19).
Sa presupunem acum ca f este
strict convexa in I.Rezultatul exprimat de (19) si obtinut in ipoteza ca f este
convexa ramane valabil si in cazul in care f este,mai mult,strict convexa.Ceea
ce se vrea este intarirea acestui rezultat pana la (20).Fie ![]() Atunci,din
partea stanga a dublei inegalitati (19) in care se inlocuieste b cu c,rezulta:
Atunci,din
partea stanga a dublei inegalitati (19) in care se inlocuieste b cu c,rezulta:
![]() . (23)
. (23)
Pe de alta parte, f fiind acum strict convexa in I,aplicatia :
![]()
este strict crescatoare,deci:
![]() (24)
(24)
La fel,aplicatia :
![]()
este strict crescatoare,deci:
![]()
care se scrie,evident:,
![]() (25)
(25)
Din partea dreapta a dublei inegalitati (19), in care se inlocuieste a cu c,rezulta:
![]() (26)
(26)
Din (23),(24),(25) si (26) rezulta:
![]()
care contine,evident,dubla inegalitate (20).
Corolar 3:
Fie f o functie numerica finita pe
intervalul ![]() ,convexa
(respectiv strict convexa) in I.Atunci:
,convexa
(respectiv strict convexa) in I.Atunci:
a) ![]() si
si ![]() sunt functii crescatoare (respectiv strict
crescatoare) pe interiorul lui I;
sunt functii crescatoare (respectiv strict
crescatoare) pe interiorul lui I;
b) multimea punctelor lui I in care f nu este derivabila este cel mult numarabila.
Demonstratie:
a)Fie,intr-adevar, ![]() si
si ![]() doua puncte interioare ale lui I cu
doua puncte interioare ale lui I cu ![]() Din teorema
1 (vezi (14)) si corolarul 2(vezi (19)),rezulta:
Din teorema
1 (vezi (14)) si corolarul 2(vezi (19)),rezulta:
![]()
din care obtinem:
![]() si
si ![]() .
.
In cazul in care f este strict convexa,in locul inegalitatii (19) se utilizeaza inegalitatea (20) si cu aceeasi tehnica ca mai inainte,obtinem:
![]() si
si ![]() .
.
b)Fie E multimea
punctelor interioare ale lui I in care f nu este derivabila.Se stie ca (vezi
teorema 1) in orice punct interior al lui I, ![]() si
si ![]() exista si
exista si ![]() .De aceea,a
spune ca x este punct interior al lui I si f nu este derivabila in x inseamna a
spune ca x este un punct interior al lui I si
.De aceea,a
spune ca x este punct interior al lui I si f nu este derivabila in x inseamna a
spune ca x este un punct interior al lui I si ![]() .Asadar:
.Asadar:
![]() x interior
lui I,
x interior
lui I, ![]()
Sa consideram ,pentru fiecare punct ![]() ,intervalul
deschis
,intervalul
deschis ![]() .Dat fiind
ca
.Dat fiind
ca ![]() ,
,![]() este
nevid.Pentru orice doua puncte
este
nevid.Pentru orice doua puncte ![]() cu
cu ![]() avem
avem ![]() ,oricare ar
fi
,oricare ar
fi ![]() si oricare ar fi
si oricare ar fi ![]() .Intr-adevar,
.Intr-adevar,
![]()
Tinand seama de ceste inegalitati si de corolarul 2(vezi (19)) rezulta:
![]() ,
,
ceea ce demonstreaza afirmatia.Ori ,daca pentru orice ![]() cu
cu ![]() avem
avem ![]() ,oricare ar
fi
,oricare ar
fi ![]() si oricare ar fi
si oricare ar fi ![]() .,aceasta
inseamna ca atunci cand x parcurge E,intervalele deschise ,nevide,
.,aceasta
inseamna ca atunci cand x parcurge E,intervalele deschise ,nevide, ![]() sunt doua cate doua fara puncte
comune.Multimea acestor intervale este deci numarabila,ceea ce atrage ca E
insusi este o multime numarabila.
sunt doua cate doua fara puncte
comune.Multimea acestor intervale este deci numarabila,ceea ce atrage ca E
insusi este o multime numarabila.
Fie f o functie convexa in I, ![]() un punct interior al lui I si (d) o dreapta ce
trece prin punctul
un punct interior al lui I si (d) o dreapta ce
trece prin punctul ![]() a carei ecuatie este:
a carei ecuatie este:
![]()
Daca ![]() este astfel incat
este astfel incat
![]() ,
,
atunci orice
punct al graficului lui f se afla deasupra dreptei (d).Daca f este strict convexa,atunci punctul
![]() este singurul punct comun al lui
este singurul punct comun al lui ![]() cu (d).Intr-adevar,fie x un punct interior al
lui I,
cu (d).Intr-adevar,fie x un punct interior al
lui I,![]() .Tinand
seama de corolarul 2(vezi(19)),avem:
.Tinand
seama de corolarul 2(vezi(19)),avem:
![]() ,
,
de unde rezulta:
![]()
sau ,inca:
![]() ,
,
adica ![]() Daca x este
punct interior al lui I astfel incat
Daca x este
punct interior al lui I astfel incat ![]() ,cu
acelea;i argumente ca mai sus,avem:
,cu
acelea;i argumente ca mai sus,avem:
![]()
sau inca
![]()
Afirmatia referitoare la cazul in care f este strict convexa se demonstreaza cu aceeasi tehnica,utilizand in locul inegalitatii (19) pe (20).
Reciproc, fie f
convexa pe I, ![]() un punct interior al lui I, si dreapta (d) de
ecuatie:
un punct interior al lui I, si dreapta (d) de
ecuatie:
![]()
Daca graficul lui f este deasupra dreptei (d),atunci:
![]() .
.
Intr-adevar,daca
pentru orice ![]() ,avem:
,avem:
![]() ,
,
adica
![]() ,
,
atunci,pentru ![]() ,din
aceasta ultima inegalitate rezulta:
,din
aceasta ultima inegalitate rezulta:
![]()
care atrage ![]() , iar
pentru
, iar
pentru ![]() rezulta:
rezulta:
![]()
care atrage ![]() ,deci,
,deci,
![]()
Definitie 7
Fie f o functie
numerica finita pe un interval ![]() O dreapta
(d) ce trece printr-un punct al graficului lui f se numeste dreapta suport la
O dreapta
(d) ce trece printr-un punct al graficului lui f se numeste dreapta suport la ![]() in acel punct daca toate punctele lui
in acel punct daca toate punctele lui ![]() sunt situate deasupra lui (d).
sunt situate deasupra lui (d).
Tinand seama de aceasta definitie si de rationamentul anterior ei,putem enunta:
Propozitie 2
Fie I un interval
al dreptei numerice , ![]() o functie numerica finita,convexa in I,
o functie numerica finita,convexa in I, ![]() un punct interior al lui I.Necesar si
suficient pentru ca o dreapta ce trece prin punctul
un punct interior al lui I.Necesar si
suficient pentru ca o dreapta ce trece prin punctul ![]() sa fie dreapta suport pentru f in acel punct
este ca coeficientul ei unghiular
sa fie dreapta suport pentru f in acel punct
este ca coeficientul ei unghiular ![]()
sa satisfaca ![]() .Daca f
este derivabila in
.Daca f
este derivabila in ![]() ,atunci
exista o singura dreapta suport la
,atunci
exista o singura dreapta suport la ![]() in punctul
in punctul ![]() ,anume
tangenta in acest punct la
,anume
tangenta in acest punct la ![]() si
reciproc.
si
reciproc.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1018
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved