| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Reducerea ecuatiei unei cuadrice la forma canonica
Ecuatia algebrica de gradul al
doilea (1.1), reprezinta din punct
de vedere geometric o suprafata dintre cele descrise in paragraful
prcedent sau multimea vida. Aceasta cuadrica este
caracterizata analitic de reletia (1.1), intr-un anume reper ortonormat R (O; ![]() ) , din spatiul punctual euclidian E = (E3,V ,~) . Pentru a recunoaste suprafata pe
care o reprezita aceasta ecuatie, vom efectua o transformare
izometrica in spatiul euclidian tridimensional E3, astfel incat caracterizarea analitica in noul reper (reper canonic) ,sa aiba cea mai simpla
forma,numita forma canonica. Transformarea izometrica t : E3 E3 , a reperului ortonormat R (O;
) , din spatiul punctual euclidian E = (E3,V ,~) . Pentru a recunoaste suprafata pe
care o reprezita aceasta ecuatie, vom efectua o transformare
izometrica in spatiul euclidian tridimensional E3, astfel incat caracterizarea analitica in noul reper (reper canonic) ,sa aiba cea mai simpla
forma,numita forma canonica. Transformarea izometrica t : E3 E3 , a reperului ortonormat R (O; ![]() ) in reperul ortonormat R ' (O';
) in reperul ortonormat R ' (O';![]() ) (reper canonic),
este perfect determinata de translatia originii t(O) = O' si de
aplicatia ortogonala asociata T :V V , care transforma baza
ortonormata
) (reper canonic),
este perfect determinata de translatia originii t(O) = O' si de
aplicatia ortogonala asociata T :V V , care transforma baza
ortonormata
in baza ortonormata .
Fie cuadrica (S E3
, caracterizata analittic in reperul cartezian R (O; ![]() ) de ecuatia :
) de ecuatia :
S a11 x2 +a22 y2 +a33 z2 +2a12 xy +2a23 yz +2a13xz +
+ 2a14 x + 2a24 y + 2a34 z + a44 = 0 (1)
Asociem cuadricei S ) matricele :

cu proprietatea aij = aji
Matricea simetrica A a suprafetei (1) determina in mod unic transformarea liniara simetrica T : V V pe care o vom numi transformarea liniara simetrica asociata suprafetei (S ) . Ecuatia caracte-ristica det( A- lI ) = 0 se poate scrie sub forma
l - Il + Jl d 0 , unde (2)
I = a11+a22+a33 , J =![]() +
+![]() +
+![]() , d = detA (3)
, d = detA (3)
Conform rezultatelor stabilite in
5,cap.7 ,valorile proprii l l l ale ecuatiei (2) sunt reale,iar
vectorii propri corespunzatori![]() sunt ortogonali. In plus, trecerea de la baza la baza
sunt ortogonali. In plus, trecerea de la baza la baza ![]() (matricea schimbarii de baza este
ortogonala, W = tW ) invariaza rang A si polinomul caracteristic (2) .
(matricea schimbarii de baza este
ortogonala, W = tW ) invariaza rang A si polinomul caracteristic (2) .
Daca efectuam o translatie t: E3 E3 ,X =X' +Xo ,matricea A, asociata cuadricei (1) , nu se modifica.
In consecinta , daca pe spatiul euclidian E3 efectuam o transformare izometrica , data de compunerea dintre o translatie si o centro-izometrie, cuadrica (S ) va fi caracterizata de matricea A'cu cantitatile I',J',respectiv d
pentru care avem :
|
1Propozitie |
Cantitatile I, J, d si rangA sunt invarianti izometrici, adicaI'= I , J' = J , d d , rangA' = rangA . |
Considerand acum matricea ![]() , D = det
, D = det![]() , cu ecuatia caracteristica det (
, cu ecuatia caracteristica det (![]() -lI ) = 0, adica
-lI ) = 0, adica
l - ![]() l + Ll - Kl D (4)
l + Ll - Kl D (4)
si
transformarea simetrica T: E4
E4, caracterizata de matricea ![]() intr-o baza ortonormata din spatiul V , rang
intr-o baza ortonormata din spatiul V , rang![]() si polinomul caracteristic raman neschimbate la o schimbare de baza , deci
cantitatile rang
si polinomul caracteristic raman neschimbate la o schimbare de baza , deci
cantitatile rang![]() ,
,![]() , L, K, D sunt invariante trecand de la o baza
ortonormata la alta baza ortonormata.
, L, K, D sunt invariante trecand de la o baza
ortonormata la alta baza ortonormata.
De observat ca o centro-izometrie a spatiului E3 care
transporta baza in baza ![]() , poate fi gandita ca o centro-izometrie
a spatiului E4 , care transporta baza in baza
, poate fi gandita ca o centro-izometrie
a spatiului E4 , care transporta baza in baza ![]() ,deci cantitatile rangA,
rang
,deci cantitatile rangA,
rang![]() ,I ,J, d D,K,L,
,I ,J, d D,K,L,![]() sunt
invarianti ai cuadricei (S ) pentru centro-izomertiile
spatiului E3 .
sunt
invarianti ai cuadricei (S ) pentru centro-izomertiile
spatiului E3 .
Pentru anumite cuadrice se demonstreaza invarianta la translatii si a cantitatilor L si K , adica L si K sunt invarianti la izometriile spatiului E
Invariantii I ,J, d D, rangA, rang![]() determina
complet toate clasele izometrice de suprafete de ordinul al doilea. Din
acest motiv, vom spune ca acestia formeaza un sistem complet de invarianti pentru suprafetele de ordinul al doilea .
determina
complet toate clasele izometrice de suprafete de ordinul al doilea. Din
acest motiv, vom spune ca acestia formeaza un sistem complet de invarianti pentru suprafetele de ordinul al doilea .
Daca doua cuadrice (S ) si (S ) sunt caracterizate de aceeasi invarianti izometrici, atunci exista o izometrie a spatiului E3 care va va aplica punct cu punct suprafata (S ) pe suprafata (S
Sa notam cu f(x,y,z) membrul stang al ecuatiei (1) si forma patratica din acest polinom prin:
j (x,y,z) = a11 x2 +a22 y2 +a33 z2 +2a12 xy +2a23 yz +2a13xz . (5)
Daca functia f ar satisface relatia f(-x,-y,-z) = f(x,y,z) , atunci , din punct de vedere geometric , cuadrica (S ) ar admite originea O(0,0,0) drept centru de simetrie pentru multimea punctelor sale. Astfel , in mod similar algoritmului aplicat la conice, vom efectua o translatie in spatiul E3 ,asa incat, in noul reper, expresia analitica a cuadricei (S ) sa nu contina termeni de gradul intai (atunci cand este posibil) .
Efecuand translatia :
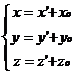 (6)
(6)
ecuatia (1) se transforma in
j (x',y',z' ) +2 ( ![]() ) + f (xo,yo,zo )
= 0 (7)
) + f (xo,yo,zo )
= 0 (7)
Sa
consideram sistemul :![]() ,sau, scris explicit,
,sau, scris explicit,
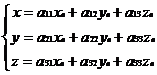 (8)
(8)
cu determinantul d Vom reduce la forma canonica cuadrica (S ) in cazurile: d 0, repectiv d
Cazul d In acest caz sistemul (8) admite o unica solutie (xo,yo,zo) adica cuadrica (S )are centru unic, punctul O'(xo,yo,zo),originea noului reper.
Dupa efectuarea translatiei (6) in punctul O' ecuatia cuadricei (S ) se scrie sub forma
j (x',y',z' ) + f (xo,yo,zo ) = 0 (9)
si folosind invarianta lui D, obtinem f (xo,yo,zo
) = ![]() .
.
Forma patratica j admite forma canonica: j (X,Y,Z ) = l X l Y l Z
in raport cu reperul format din
vectorii proprii ![]() , corespunzatori valorilor proprii l l l , radacinile ecuatiei
caracteristice (2). Astfel, in reperul R''(O';
, corespunzatori valorilor proprii l l l , radacinile ecuatiei
caracteristice (2). Astfel, in reperul R''(O';
![]() ) cuadrica (S ) admite forma canonica :
) cuadrica (S ) admite forma canonica :
l X l Y l Z + ![]() = 0 (10)
= 0 (10)
Reperul R''(O';
![]() ) va fi numit reper canonic ,iar ecuatia (10) va
fi numita ecuatia redusa .
) va fi numit reper canonic ,iar ecuatia (10) va
fi numita ecuatia redusa .
Ecuatia (10) reprezinta pentru
D
elipsoid daca l l l sunt de acelasi semn, contrar semnului termenului liber ![]()
hiperboloid daca numai doua valori proprii au acelasi semn
multimea
vida daca l l l , ![]() au acelasi semn
au acelasi semn
D
con daca l l l <
punct dublu daca l l l au acelasi semn
Cazul d In acest caz sistemul (8) poate fi incompatibil -cuadrica nu are centru, compatibil simplu nedeterminat -cuadrica are o dreapta de centre, sau este compatibil dublu nedetermint, caz in care cuadrica admite un plan de centre . Pentru a determina reperul canonic, vom efectua in spatiul E3 o centro-izometrie urmata de o translatie ,convenabil aleasa .
Daca d l l l 0 si D , atunci ecuatia caracteristica are cel putin o radacina egala cu zero.
Sa presupunem ca l si celelalte diferite de zero. Ecuatia caracteristica se scrie sub
forma l l -Il+J)=0, in care J = l l 0. Ecuatia cuadricei, raportata
la reperul ortonormat, format din vectorii proprii ![]() corespunzatori
valorilor proprii l l l se
scrie sub forma:
corespunzatori
valorilor proprii l l l se
scrie sub forma:
l x'2 + l y'2 + 2a'14x' +2a'24y' + 2a'34z' + a'44 = 0 (11)
Calculand invariantul izometric D pentru aceasta ecuatie obtinem
D = - (a'34)2J, din care pentru D rezulta a'34
= ![]()
![]()
Sa efectuam in spatiul E3 translatia :
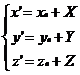 (12)
(12)
atunci ecuatia (11) se scrie
l X2 + l Y2 + 2 a'34 Z + 2(l xo+a'14)X +2(l yo+a'24)Y +
+ l xo2 +l yo2 +2a'14xo+2a'24yo+2a'34zo+a'44 = 0 (13)
Alegand
xo=![]() , yo=
, yo=![]() , zo=
, zo=![]() (l xo2+l yo2+2a'14xo+2a'24yo+2a'34zo+a'44)
(l xo2+l yo2+2a'14xo+2a'24yo+2a'34zo+a'44)
ecuatia (13) devine
l X l Y ![]() Z = 0 (14)
Z = 0 (14)
ceea ce reprezinta un paraboloid,eliptic sau parabolic dupa cum l l > sau l l <
Pentru D , din calculul invariantului D in ecuatia (11), rezulta a'34 = 0
caz in care ecuatia (11) se reduce la o ecuatie de gradul doi in doua nedeterminate, ce poate fi pusa sub forma :
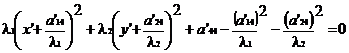 (15)
(15)
Daca efectuam translatia x = X - ![]() ,
,![]() , z = Z si
notam cu
, z = Z si
notam cu
![]()
![]() , ecuatia (15) se scrie
, ecuatia (15) se scrie
l X l Y + ![]() 0 (16)
0 (16)
Calculand cantitatile L si K pentru
ecuatiile (11) si (16) constatam invarianta acestora si obtinem K =l l ![]() = J
= J![]() , adica
, adica ![]()
![]() .
.
In acest caz ecuatia (16) reprezinta:
pentru K , un
cilindru (eliptic daca l l > , hiperbolic daca l l < ) sau multimea vida daca l l , ![]() au acelasi semn
au acelasi semn
pentru K = 0 , plane secante daca l l < sau o dreapta dubla daca l l >
Sa presupunem ca d l l l 0 pentru l l = 0 si l 0, de unde rezulta ca J = 0 si l = I .
In reperul R'(O; ![]() ) determinat de
vectorii proprii corespunzatori valorilor proprii l l l ecuatia (1) se
scrie sub forma:
) determinat de
vectorii proprii corespunzatori valorilor proprii l l l ecuatia (1) se
scrie sub forma:
l x'2 + 2a'14x' +2a'24y' + 2a'34z' + a'44 = 0 (17)
sau
l1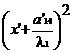 + 2a'24y'
+ 2a'34z' + a''44 = 0 (17)'
+ 2a'24y'
+ 2a'34z' + a''44 = 0 (17)'
unde a''44
= a'44 - ![]() .
.
Efectuand translatia ![]() , y' = y'' , z' =
z'',in urma careia ecuatia (17) se scrie
, y' = y'' , z' =
z'',in urma careia ecuatia (17) se scrie
l x''2 +2a'24y'' + 2a'34z'' + a''44 = 0 (17)''
si centro-izometria :
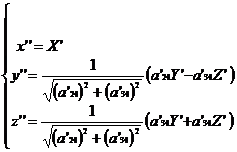 , pentru
, pentru ![]()
obtinem
l X' 2 + 2 k1Y' + a''44 = 0 (18)
unde k1= ![]() . In final,
translatia :
. In final,
translatia : ![]() ne conduce la forma canonica
ne conduce la forma canonica
l X 2 + 2 k1Y = 0 . (19)
Invarianta lui K
= -(k1)2I 0 la centro-izometrii si
respectiv la translatii (se demontreaza direct) ne procura k1 = ![]() ,adica forma
canonica (19) poate fi pusa sub forma
,adica forma
canonica (19) poate fi pusa sub forma
X 2 ![]() 2
2![]() Y = 0 (20)
Y = 0 (20)
si reprezinta un cilindru parabolic .
Pentru ![]() a'24 = a'34
= 0, rezulta K = 0 si ecuatia (17)'' se
reduce la
a'24 = a'34
= 0, rezulta K = 0 si ecuatia (17)'' se
reduce la
l x''2 + a''44 = 0 (21)
Calculand acum valoarea lui L se gaseste L =
l a'' = I a , din care obtinem a = ![]() sin deci
ecuatia redusa
sin deci
ecuatia redusa
X 2
+ ![]() = 0 (22)
= 0 (22)
Care reprezinta plane paralele (confundate) pentru L 0 ,respectiv multimea vida daca L >
Rezultatele obtinute reprezinta clasificarea izometrica a cuadricelor,
pe care oconcentram in urmatorul tabel:
|
D |
d |
Discutie |
||
|
D cuadrice nedegene-rate |
d 0 - cu centru |
elipsoizi,hiperboloizi sau multimea vida |
||
|
d = 0 -fara centru |
paraboloizi |
|||
|
D cuadrice degenerate |
d 0 - cu centru |
conuri sau punct dublu |
||
|
d cu dr. de centre, cu plan de centre sau fara centru |
J cu dreapta de centre |
K |
cilindri sau multimea vida |
|
|
K = |
plane secante sau o dreapta dubla |
|||
|
J cu plan de centre sau fara centru |
K |
cilindri parabolici |
||
|
K = |
Plane paralele (confundate) sau multimea vida |
|||
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3746
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved