SIRUL LUI FIBONACCI

SIRUL LUI FIBONACCI

Fibonacci este cunoscut dupa un pasaj din Liber Abaci care a condus la un miracol matematic. Paragraful se refera la o problema cu iepuri: cate perechi de iepuri se vor naste in decursul unui an dintr-o pereche originala, presupunand ca in fiecare luna fiecare pereche produce alta pereche si ca iepurii incep sa se reproduca de la varsta de doua luni. Lasam acest exercitiu pe seama cititorului. Fibonacci a presupus ca perechea originala incepe sa se reproduca la varsta de doua luni si ca da nastere unui perechi de iepuri in fiecare luna. In luna a patra, primii nascuti incep sa se reproduca. Dupa ce procesul incepe, numarul total de perechi de iepuri la finalul fiecarei luni este urmatorul: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233. Fiecare numar este egal cu suma celor doua numere de dinainte. Daca iepurii ar fi continuat sa se inmulteasca timp de 100 de luni, numarul total de perechi de iepuri ar fi 354.224.848.179.261.915.075! Seria (sau sirul) lui Fibonacci este mai mult decat o sursa de amuzament. Daca se imparte oricare numar din serie la numarul imediat urmator, rezultatul este 0,618. Daca se imparte oricare numar din serie la numarul precedent, rezultatul este 1,618. Aceste doua numere - 0,618 si 1,618 - erau cunoscute deja in istorie. Ele se numesc, sintetizate, "proportia de aur". Aceasta proportie defineste dimensiunile Partenonului, a cartilor de joc si de credit, precum si proportiile cladirii Natiunilor Unite din New York. Orizontala unei cruci crestine taie verticala la aceeasi proportie: partea de sus este 61 % din cea de jos. "Proportia de aur" sau "Numarul de aur" se gaseste in natura si la om. Lungimea oaselor carpiene la palma umana au aceeasi proportie. Partea de sus a corpului uman, masurata de la crestet pana la ombilic, este 61 % din partea de jos, masurata

de la ombilic pana la picioare. Proprietatile sirului lui Fibonacci sunt fascinante si au aplicatii si in analiza tehnica a actiunilor. Investitorii, mai bine zis analistii tehnici, folosesc variante ale sirului pentru predictiile miscarii pietelor financiare. Asemenea predictii functioneaza doar atat cat sa mentina entuziasmul. Universitatea

din Santa Clara are chiar si o asociatie Fibonacci, care publica mii de pagini pe marginea subiectului. Cartea Liber Abaci a lui Leonardo Fibonacci Pisano din 1202 a fost un pas spectaculos in transformarea masurarii intr-un element-cheie al calculului riscului. Societatea in care traia Fibonacci nu era inca pregatita sa ataseze numere conceptului de risc. In acel timp, riscul era inca legat de capriciile naturii. Mai intai, oamenii au trebuit sa recunoasca riscurile create de om si sa acumuleze curajul de a infrunta destinele pana sa accepte tehnicile de masurare a riscului. Aceasta acceptare era inca la cel putin 200 de ani distanta in viitor.

Numerele lui Fibonacci

La inceputul secolului al XIII-lea , in orasul Pisa din Italia a trait un matematician iscusit, mare cunoscator al diferitelor relatii dintre numere pe care il chema Leonardo.Ii ziceau si Fibonacci , adica fiul lui Bonacci din Pisa.In 1202 el a publicat in limba latina o carte intitulata " Cartea despre abac" (Incipit Liber Abacci compositus a Leonardo filius Bonacci Pisano), care cuprindea ansamblul cunostintelorde aritmetica si algebra de la acea data.Cartea lui a fost una din primele din Europa care invata cum trebuie folosit sistemul zecimal.

Cartea lui Leonardo din Pisa a cunoscut o larga raspandire in timp de peste 2 secole a fost considerata cea mai competenta sursa de cunostinte in domeniul numerelor.

Potrivit obiceiului din acea epoca, Fibonacci a participat la concursuri matematice- dispute publice pentru cea mai buna si mai rapida solutie a unor probleme grele, ceva in genul concursurilor pe tara din zilele noastre!

Iscusinta de care dadea dovada Leonardo in rezolvarea problemelor cu numere uimise pe toata lumea.

Marea reputaie a lui Fibonacci a facut ca imparatul Germaniei Frederic II sa vina in 1225 la Pisa, insotit de un grup de matematicieni, care doreau sa il supuna pe Fibonacci la un examen public.Una din problemele date spre rezolvare suna astfel:

-sa se gaseasca un patrat perfect , care ramane patrat perfect daca este marit sau micsorat cu 5.Dupa un timp de gandire , Fibonacci a gasit numarul cautat.Era fractia:sau

Intr-adevar: -5= si +5=

Sau

-5= si +5=

Nu cunoastem rationamentul lui Fibonacci , dar problema a fost rezolvata in mod stralucit.

Se poate ca presupunera lui Viaceslav Nezabudkin, student la Institutul Silvic din orasul Ioskar-Ola, sa nu fie departe de adevar.

-Nu cumva Fibonacci a plecat de la reprezentarea geometrica a oricarui patrat perfect ca suma unor numere impare ordinale?

Pornind de la aceasta ipoteza, Viaceslav Nezabutkin a gasit o solutie originala a problemei lui Fibonacci, care este interesanta tocmai prin fatpul ca se apropie de metodele folosite pe timpul lui Fibonacci.

Reproducem cu mici schimbari aceasta solutie.Intreptand gnomonii care completeaza patratul unitate pana la orice patrat intreg , fig a) obtinem o figura in forma de scara, cu trepte egale de cate 2 casute care se poate continua la infinit, b).Intrerupand aceasta figura la orice coloana din dreapta obtinem o serie de figuri in scara care reprezinta toate numerele intregi patrate perfecte.Figura ne arata ca printre numerele intregi- patrate perfecte- nu se afla si nici nu se pot afla numere care sa satisfaca conditia problemei.Deci numarul cautat este o fractie de forma .

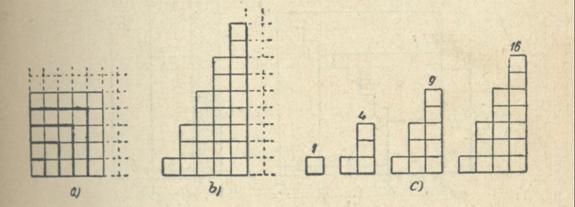
Dup ace scadem si adunam 5 la si aducem la acelasi numitor obtinem:

respectiv

Potrivit enuntului. , sunt numere intregi, patrate perfecte.Asemenea numere exista , cu conditia ca sa existe doi gnomoni alaturati si egali de forma BEFGDC si EHJKGF(fig 223.a)).

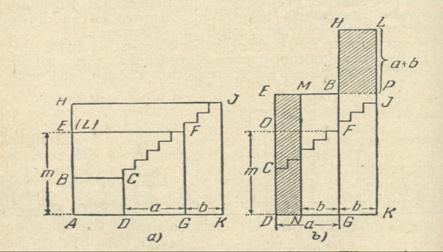
avand fiecare un numar de 5n² casute.Atunci scazand din patratul AEFG (m²) gnomonul BEFGDC (5n²), obtinem patratul ABCD (m² - 5 n²), iar adaugand la numarul AEFG gnomonul EHJKGF(5n²), obtinem patratul AHJK (m²+5n²).Sa gasim aceste numere gnomonii pe linia franta JFC, iar din fragmentele obtinute construim dreptunghiurile DEBG si GHLK.(fig b))

Luam GN=GK=b si ducem NM ll DE.Deoarece DEBG si GHLK au ariile egale, aria BHLP=aria DEMN. Deci,

= sau =

Prin urmare, =.

E firesc sa presupunem ca, de exemplu, a este multiplu de 5 , adica a=5k, unde k=1,2,3,4n . Atunci si b= 4k, find singura valoare posibila a lui b care transforma aceasta fractie intr-un numar intreg - patrat.Totodata, in urma calculelor, constatam ca n=6k.

Asadar, a=5k, b=4k,n=6k.Numitorul fractiei cautate n²=(6k)² .Sa aflam si numaratorul. Avem: ED=

Mai departe, m=FG dar FG=EC si FG=O, de asemenea OC=OF=a

ED=EC+OD-OC, sau ED=2EC - a ; de unde EC= si m=FG=EC=

Fractia cautata : 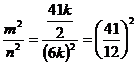, adica numarul gasit de Fibonacci.

*Toate incercarile, chiar si cele mai ingenioase, de a rezolva aceasta problema cu ajutorul algebrei, duc in cel mai bun caz la o ecuatie de gradul patru cu doua necunoscute.

Sirul lui Fibonacci

Fibonacci a intocmit un sir de numere naturale, care ulterior s-a dovedit foarte folositor:

1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 ,..

Legea formarii termenilor acestui sir este foarte simpla: primii 2 termeni sunt unul, iar fiecare termen urmator se obtine prin adunarea celor 2 termeni care il preced.De exemplu 2=1+1 3=1+2 5=2+3 8=3+5.etc

Un paradox

De numerele lui Fibonacci este legat indirect un interesant paradox geometric.Este evident ca daca o figura plana va fi sectionata in mai multe fragmente si apoi se vor alatura fragmentele (fara a le suprapune), se va putea obtine o figura noua, a carei forma se va deosebi de cea initiala , dar a carei arie va ramane aceiasi; aria nu poate sa creasca sau se sa micsoreze nici macar cu un milimetru patrat.Acest adevar evident este considerat in geometrie drept una din tezele fundamentale pe care se bazeaza teoria masurartii suprafetelor.

In figura se arata transformarea unui patrat intr-un dreptunghi.Patratul este taiat in doua triunghiuri egale si in doua trapeze egale.Pentru moment, notam cu x si y lungimea laturilor lor.Alcatuim din aceste fragmente un dreptunghi.Daca o astfel de transformare a unui patrat intr-un drepunghi este cu adevarat posibila, atunci care sunt valorile lui x si y la care trebuie impartita latura patratului?

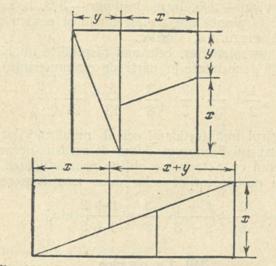
Ca sa se demonstreze acest lucru s-a desenat pe o foaie de hartie din caietul de matematica un patrat cu 64 de casute, in scopul determinarii laturii patratului ca sa se obtina segmentele x si y.Mai intai s-a crezut ca lungimea lor nu are importanta si s-a luat x=6 si y=2.Desenand patratul si taindu-l in doua triunghiuri egale si doua trapeze egale, s-a incercat sa se construiasca un dreptunghi, dar nu a iesit nimic.Dreptunghiul nu se forma, numai daca x=5 si y=3.Astfel s-a izbutit sa se alcatuiasca un dreptunghi din fragmentele patratului, dar a aparut un alt impediment: suprafata dreptunghiului era de 65 de casute, adica avea o casuta mai mult decat suprafata patratului sectionat.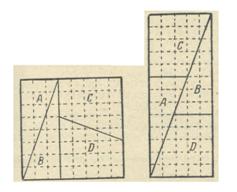

Intr-adevar, lungimea dreptunghiului trebuie sa cuprinda x+x+y=13 (unitati).Latimea dreptunghiului este egala cu x si dreptunghiul meu are o latime de 5 patratele, deci , suprafata lui are 5x 13 =65 patratele.Dar aceasta nu este totul.folosind aceleasi linii de taiere, s-a sectionat un alt patrat cu latura de 13 patratele.Luand x=8 si y=5 se va forma un dreptunghi care va avea suprafata mai mica tot cu o unitate.

Suprafata patratului= 13² =169 patratele

Suprafata dreptunghiului = (2x+y)x=168 patratele

Cel care a studiat aceasta problema a fost prea increzator in vederea sa , netinand seama de demonstratiile matematice.Se pare ca un dreptunghi perfect nu s-a format niciodata din fragmentele patratului , in mod obligatoriu trebuiau sa se formeze anumite interstitii., poate invizibile cu ochiul liber sau sa aibe loc o suprapunere a unuia din fragmente cu un altul.

Sa luam de exemplu cazul in care patratul de 64 de casute a fost impartit in doua: 5 respectiv 3 unitati.Unind triunghiul A cu trapezul C si triunghiul B cu trapezul D , conform figurii, nu se poate obtine contopirea liniilor EFK si EHK in diagonala EK, deoarece liniile EFK si EHK sunt usor frante in F si H.

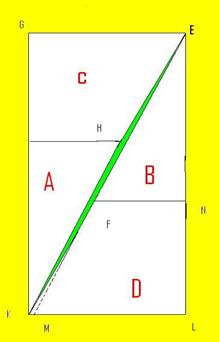
Se poate demonstra usor: fie M in care se intretaie latura KL cu prelungirea laturii EF.Din asemanarea triunghiurilor rezulta ; in timp ce KL=5.Deci M nu coincide cu K,de unde rezulta ca liniile EFK si EHK sunt frante.

Raman de analizat urmatoarele situatii:

1) de ce diferenta era de exact 1 casuta ?

2) cum trebuie impartite laturile patratului pentru a obtine un dreptunghi compact.

Cu ajutorul algebrei se demonstreaza ca :

Aria patratului este (x+y)²=x²+2xy+y²

Aria dreptunghiului este (2x+y)x=2x²+xy

Prin scaderea celor doua relatii R=x²-xy-y² .Ariile dreptunghiului si patratului vor fi egale doar daca R=0.

X²-xy-y²=0.Prin impartirea cu y² o sa avem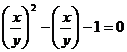.Notand x/y cu a , rezulta:

. De aici aflam a_1,2= Se ia in considerare valoarea pozitiva si

*Numai in ipoteza acestui raport ale partilor x si y este posibila transformarea integrala a patratului in dreptunghi.Daca x si y au valori rationale, R nu va putea fi niciodata egal cu 0.|Daca y si x au valori intregi, cea mai maica diferenta posibila intre suprafete este 1. Aceasta minima diferenta intreaga nu s-a observat luandu-se valori pentru x si y doua numere alaturate din firul lui Fibonacci .