| CATEGORII DOCUMENTE | ||
|
||
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Spatiu vectorial in raport cu un corp K
Definitia 1.1. Se numeste spatiu vectorial (liniar) in raport cu corpul K, multimea X nevida, inzestrata cu o lege de compozitie interna (notata aditiv si numita adunare):
"+" : X X X,
o lege de compozitie externa (notata multiplicativ si numita inmultire cu scalar):
" " : K X X,
care au urmatoarele proprietati:
(i). (x + y) + z = x + (y + z), ( ) x, y, z I X (asociativitate);
(ii). ( ) in X un element, notat 0, numit element neutru, astfel ca
x + 0 = 0 + x = x, ( ) xIX
(iii). ( ) x I X, ( ) in X un element, notat - x, numit opusul elementului x, astfel ca: x + (- x) = (- x) + x = 0;
(iv). x + y = y + x, ( ) x, y I X (comutativitate);
(v). a b x = a x + b x, ( a bIK, xIX
(vi). a ( x + y) = a x + a y, ( aIK, x, yIX
(vii). a b x = a b x), ( a bIK, xIX
(viii). Daca 1I K atunci 1 x = x, ( ) xI X.
Elementele spatiului vectorial X le vom numi vectori, iar elementele corpului K le vom numi scalari. Elementul 0 se mai numeste elementul nul al spatiului X.
Corpul K este unul din corpurile R al numerelor reale sau corpul C al numerelor complexe; daca K º R atunci X se numeste spatiu vectorial real, iar daca K º C spatiul X se numeste spatiu vectorial complex.
Exemple: 1). Produsul cartezian Kn = K K K, adica multimea:
Kn
formeaza o structura de spatiu vectorial peste corpul K, daca definim operatiile de adunare si inmultire cu scalari astfel:
(x1, x2, ..,xn) + (y1, y2, .,yn) = (x1 + y1, x2 + y2,., xn + yn)
si
a (x1, x2, .xn) = (ax1, ax2, ., axn)
Vectorul nul este in acest caz vectorul 0 = (0, 0, .,0), iar opusul vectorului
x = (x1, x2, .xn) este vectorul -x = (-x1, -x2, .-xn).
2). Multimea polinoamelor de o nedeterminata, de grad cel mult n (nIN), cu coeficienti intr-un corp K, in raport cu operatiile de adunare a polinoamelor si de inmultire a polinoamelor cu un element din corpul K.
Cazuri particulare:
Rn ,
Cn .
3). Multimea sirurilor x = (xn)nIN de numere reale sau complexe, care satisfac conditia de marginire:
xn £ a(x), ( ) nIN
a(x) fiind un numar pozitiv care depinde de x, cu legile de compozitie astfel definite:
(xn)nIN + (yn)nIN = (xn + yn)nIN
a (xn)nIN = a (xn)nIN aIK
(4). Multimea C0[a,b] = a functiilor continue pe intervalul inchis [a,b] in raport cu operatiile:
(f + g)(t) = f(t) + g(t), ( ) tI[a,b],
(a f )(t) = a f(t) , ( ) aIR, tI[a,b].
5). Multimea Mm,n(K) a matricelor cu m linii si n coloane cu elemente numere reale (sau complexe) formeaza un spatiu vectorial peste corpul R (sau C), in raport cu operatiile de adunare a matricelor de acelasi tip si de inmultire a matricelor cu un scalar.
Daca A,B![]() Mm,n(K), A =
Mm,n(K), A = ![]() , B =
, B = ![]() se defineste suma celor doua matrice ca fiind
matricea
se defineste suma celor doua matrice ca fiind
matricea
S = A+B, S![]() Mm,n(K), S =
Mm,n(K), S = ![]() ,
sij = aij + bij
,
,
sij = aij + bij
, ![]() ,
,
iar inmultirea cu scalari a unei matrice este tot o matrice definita astfel:ESV
(α,A)![]() αA,
αA
αA,
αA![]() Mm,n(K),
Mm,n(K),
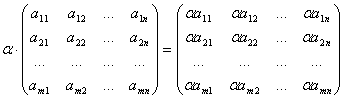 .
.
6). Spatiul vectorial al vectorilor liberi.
Notam prin E spatiul geometric punctual (adica multimea punctelor din spatiul ambiant).
Definitia 1.2. O pereche ![]() E
E ![]() E se numeste segment orientat din E , de origine
E se numeste segment orientat din E , de origine ![]() si extremitate
si extremitate ![]() .
Acesta se noteaza
.
Acesta se noteaza ![]() .
Lungimea segmentului orientat
.
Lungimea segmentului orientat ![]() se numeste modulul acestuia si se noteaza |
se numeste modulul acestuia si se noteaza |![]() |.
|.
Definitia 1.3. Doua segmente orientate ![]() si
si ![]() se numesc echipolente
daca patrulaterul
se numesc echipolente
daca patrulaterul ![]() este paralelogram. Se noteaza
este paralelogram. Se noteaza ![]() ~
~![]() .
.
Relatia de echipolenta definita mai sus are urmatoarele proprietati, a caror justificare este imediata:
a). ![]() ~
~![]() ;
;
b). ![]() ~
~![]()
![]()
![]() ~
~![]() ;
;
c). ![]() ~
~![]() si
si ![]() ~
~![]()
![]()
![]() ~
~![]() ;
;
deci relatia " ~" este o relatie de echivalenta in multimea segmentelor orientate.
Definitia 1.4. O clasa de echivalenta in raport cu relatia de echipolenta in multimea segmentelor orientate din E se numeste vector liber.
Deci un vector liber poate fi considerat ca fiind multimea segmentelor orientate echipolente cu un vector dat.
Deoarece doua segmente orientate echipolente au module egale, aceeasi directie (adica dreptele care unesc extremitatilelor au aceeasi directie) si aceeasi orientare, rezulta ca modulul, directie si sensul, comune tuturor segmentelor orientate dintr-o clasa de ecxhivalenta, sunt elemente ce caracterizeaza vectorii liberi.
Vom nota vectorii liberi prin ![]() ,
multimea vectorilor liberi prin V V = S3 ~),
iar modulul vectorului
,
multimea vectorilor liberi prin V V = S3 ~),
iar modulul vectorului ![]() prin ||
prin ||![]() ||.
||.
Constructia notiunii de vector liber este sugerata in figura urmatoare:
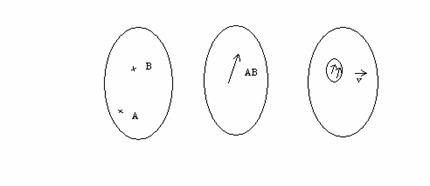
E ![]() S
S ![]() V
V
Propozitia 1. Orice vector liber admite reprezentare unica printr-un segment orientat in orice punct din spatiul E
Demonstratie.
Fie vectorul ![]() si un punct
si un punct ![]() E Notam cu
E Notam cu ![]() sfera de centru
sfera de centru ![]() si de raza ||
si de raza ||![]() ||.
Aceasta este intersectata de dreapta ce trece prin
||.
Aceasta este intersectata de dreapta ce trece prin ![]() si
are directia lui
si
are directia lui ![]() ,
in doua puncte
,
in doua puncte ![]() si
si
![]() .
Unul singur dintre segmentele orientate
.
Unul singur dintre segmentele orientate ![]() si
si ![]() are
sensul lui
are
sensul lui ![]() si acesta este cel cautat.
si acesta este cel cautat.
Doi vectori liberi sunt egali daca si numai daca au module egale, aceeasi directie si orientare.
Definitia
1.5. Se numeste adunare a
vectorilor liberi legea de compunere ![]() V
V ![]() V
V ![]() V care asociaza vectorilor
V care asociaza vectorilor ![]() si
si ![]() ,
vectorul
,
vectorul ![]() definit
prin regula triunghiului sau regula paralelogramului, reprezentate in
continuare:
definit
prin regula triunghiului sau regula paralelogramului, reprezentate in
continuare:
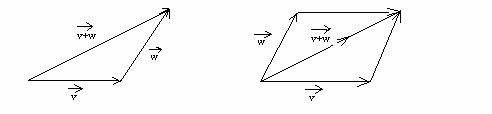
Propozitia 2. Multimea V a vectorilor liberi poseda o structura de grup abelian in raport cu adunarea.
Demonstratia este imediata.
Definitia 1.6. Se
numeste amplificatul vectorului liber ![]() prin scalarul
prin scalarul ![]() ,
vectorul
,
vectorul ![]() definit astfel:
definit astfel:
a). ![]() ;
;
b). pentru ![]() orientarile
vectorilor
orientarile
vectorilor ![]() si
si ![]() coincid iar pentru
coincid iar pentru ![]()
acestea sunt opuse;
c). directia lui ![]() coincide cu cea a lui
coincide cu cea a lui ![]() .
.
Se demonstreza cu usurinta urmatorul rezultat:
Propozitia 3. Pentru orice ![]() V si
V si ![]() avem:
avem:
a). ![]() ;
;
b). ![]() ;
;
c). ![]() ;
;
d). ![]()
Din propozitiile 1 si 2 rezulta urmatorul rezultat
Teorema 1. Multimea V a vectorilor liberi poseda o structura de spatiu vectorial peste corpul numerelor reale in raport cu operatiie de adunare si amplificare a vectorilor cu scalari.
Observatie. Notand cu E planul punctual, o constructie identica cu cea de mai sus ne permite sa obtinem spatiul V al vectorilor liberi din plan.
Operatii cu vectori
Produsul scalar
Se numeste produs scalar din V aplicatia:
definita prin:
![]() .
.
Daca ![]() si
si ![]() atunci
atunci ![]() .
.
Produsul vectorial
Dati fiind vectorii ![]() si
si ![]() se numeste produs vectorial al lor, vectorul:
se numeste produs vectorial al lor, vectorul:
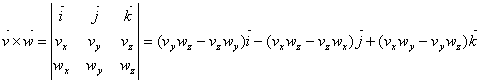
Produsul mixt
Dati fiind vectorii ![]() ,
,![]() si
si ![]() se numeste produs mixt scalarul:
se numeste produs mixt scalarul:
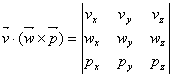
Dublul produs vectorial
Se numeste dublu produs vectorial vectorul ![]() .
.
Reguli de calcul intr-un spatiu vectorial:
(i). 0 x = 0, a 0 = 0, ( )aIK, xIX;
(ii). a x = 0 Þ a = 0 sau x = 0;
(iii). (- a) x = - a x, a (-x) = -a x, ( )aIK, xIX.
Definitia 1.2. Se numeste produs scalar pe spatiul vectorial X peste corpul K
(= R, sau C), o functie ps : X X K, cu urmatoarele proprietati:
(i). ps(x, y) = ![]() ;
;
(ii). ps(a x+b y, z) = a ps(x, z) +b ps(y, z);
(iii). ps(x, x) ³ 0; ps(x, x) = 0 Û x = 0.
Valoarea reala x
= ![]() se numeste lungimea sau norma
vectorului x.
se numeste lungimea sau norma
vectorului x.
Definitia 1.3. Un spatiu vectorial (peste corpul K) inzestrat cu un produs scalar se numeste spatiu vectorial euclidian (daca K = R), sau spatiu unitar (daca K = C).
Exemplu. Spatiul euclidian al vectorilor liberi.
Produsul
scalar al vectorilor din V este
aplicatia "." : V ![]() V
V ![]() R, definita prin
R, definita prin ![]() .
.
Dependenta si independenta liniara
Fie X un spatiu vectorial peste corpul K.
i
=1,2,.,m; j =1,2,.,ri Vectorul
x![]() X
este o combinatie liniara de vectorii xi (i=1, 2, ., m) din X, daca el se poate reprezenta
astfel:
X
este o combinatie liniara de vectorii xi (i=1, 2, ., m) din X, daca el se poate reprezenta
astfel:
![]() .
.
Observatii (i). Vectorul nul este combinatie liniara de orice familie de vectori.
(ii). Daca vectorul x este o combinatie liniara de vectorii xi (i=1, 2, ., m) si fiecare vector xi este o combinatie liniara de vectorii yij (i =1,2,.,m; j =1,2,.,ri), atunci x este o combinatie liniara de vectorii yij (i =1,2,.,m; j =1,2,.,ri).
Intr-adevar:
![]() ;
;
![]() ,
j =1,2,.,ri; i =1,2,.,m,
,
j =1,2,.,ri; i =1,2,.,m,
prin urmare:
![]() ,
i =1,2,.,m; j =1,2,.,ri .
,
i =1,2,.,m; j =1,2,.,ri .
Definitia . Vectorii ![]() I - familie de indici, se numesc liniar independenti, daca
I - familie de indici, se numesc liniar independenti, daca ![]() ;
in caz contrar vectorii se numesc liniar
dependenti, adica vectorii
;
in caz contrar vectorii se numesc liniar
dependenti, adica vectorii ![]() sunt
liniar dependenti, daca exista cel putin un
sunt
liniar dependenti, daca exista cel putin un ![]() ,
astfel ca
,
astfel ca ![]() .
.
Teorema . Un sistem de vectori ![]() este
liniar dependent daca si numai daca exista cel putin un indice
este
liniar dependent daca si numai daca exista cel putin un indice ![]() astfel
ca xj
sa fie o combinatie liniara de vectorii
astfel
ca xj
sa fie o combinatie liniara de vectorii ![]() .
.
Demonstratie. Fie ![]() ;
luand
;
luand ![]() rezulta
rezulta ![]() ,
deci vectorii
,
deci vectorii ![]() sunt liniar dependenti.
sunt liniar dependenti.
Reciproc, fie ![]() ;
inmultim relatia precedenta cu
;
inmultim relatia precedenta cu ![]() si obtinem
si obtinem
![]() ,
,
unde
![]() .
.
Teorema . Un sistem de vectori ![]() este liniar independent daca si numai daca
orice vector
este liniar independent daca si numai daca
orice vector ![]() poate
fi scris in cel mult un mod ca o combinatie liniara de vectorii
poate
fi scris in cel mult un mod ca o combinatie liniara de vectorii ![]() ,
adica daca si numai daca din combinatia liniara:
,
adica daca si numai daca din combinatia liniara:
![]() ,
,
rezulta ca scalarii ![]() sunt unic determinati de x.
sunt unic determinati de x.
Demonstratie. Suficienta. Presupunem ca in relatia: ![]() ,
,
scalarii sunt unic determinati de x. Luam, in particular, x = 0, caz in care rezulta:
![]() ;
;
deoarece aceasta relatie are loc numai pentru scalarii ![]() ,
vectorii
,
vectorii ![]() sunt liniar independenti.
sunt liniar independenti.
Necesitatea. Presupunem ca vectorii ![]() sunt
liniar independenti; atunci
sunt
liniar independenti; atunci ![]()
![]() .
.
Definitia . O multime ![]() se
numeste liniar independenta, daca
orice parte finita a ei este formata din vectori liniari independenti.
se
numeste liniar independenta, daca
orice parte finita a ei este formata din vectori liniari independenti.
Definitia . O multime liniar independenta maximala de vectori din A se numeste baza a multimii A.
Definitia . Daca multimea A (in particular spatiul X) are o baza finita atunci se spune ca A (respectiv X) are dimensiune finita; in caz contrar se spune ca A (respective X) are dimensiune infinita.
Teorema . Daca vectorii xi (i =1,2,,m) constituie o baza a multimii A atunci reprezentarea
unui vector x![]() A
ca o combinatie liniara de vectorii xi (i =1,2,,m) este unica.
A
ca o combinatie liniara de vectorii xi (i =1,2,,m) este unica.
Demonstratie. Presupunerea ca ar admite doua reprezentari este contradictorie.
x![]()
Definitia
. Daca xi (i
=1,2,,m) este o baza, scalarii ![]() pentru care are loc relatia
pentru care are loc relatia ![]() ,
determinati in mod unic de vectorul x, se numesc coordonatele vectorului x in baza xi (i =1,2,,m).
,
determinati in mod unic de vectorul x, se numesc coordonatele vectorului x in baza xi (i =1,2,,m).
Subspatii vectoriale
Definitia . Fie X un spatiu vectorial si X0![]() X. Daca X0 este parte stabila fata de adunarea vectorilor
(adica
X. Daca X0 este parte stabila fata de adunarea vectorilor
(adica ![]() )
si fata de inmultirea cu scalari a vectorilor (adica
)
si fata de inmultirea cu scalari a vectorilor (adica ![]() )
atunci X0 se numeste subspatiu vectorial al lui X.
)
atunci X0 se numeste subspatiu vectorial al lui X.
Teorema . Orice intersectie de subspatii vectoriale ale lui X este un subspatiu vectorial al lui X.
Demonstratie. Fie Xi![]() X subspatii vectoriale ale lui X,
X subspatii vectoriale ale lui X, ![]() -
familie de indici.
-
familie de indici.
Notam: ![]() ;
;
![]() .
.
![]() .
.
Analog ![]() ,
prin urmare X0 este subspatiu vectorial al lui X.
,
prin urmare X0 este subspatiu vectorial al lui X.
Definitia . Fie ![]() o
parte a lui X. Se numeste subspatiu
vectorial generat de A, sau acoperirea liniara a lui A,
cel mai mic subspatiu vectorial cae include pe A, adica intersectia
tuturor subspatiilor vectoriale care include pe A.
o
parte a lui X. Se numeste subspatiu
vectorial generat de A, sau acoperirea liniara a lui A,
cel mai mic subspatiu vectorial cae include pe A, adica intersectia
tuturor subspatiilor vectoriale care include pe A.
Notam:
![]() -
subspatiul vectorial generat de A, adica
-
subspatiul vectorial generat de A, adica ![]() Xi
- subspatiu vectorial;
Xi
- subspatiu vectorial;
![]() -
multimea tuturor combinatiilor liniare de elemente din A, adica:
-
multimea tuturor combinatiilor liniare de elemente din A, adica:
![]() .
.
Teorema . ![]() .
.
Demonstratie. ![]()
![]() .
.
Orice combinatie liniara de
elemente din A apartine oricarui subspatiu care include pe A,
deci ![]() .
.
In cele ce urmeaza ne vom situa in spatiul euclidian Rn in care produsul scalar este definit astfel:
ps : Rn Rn R,
ps(x,
y)
= ![]() ,
x
= (x1, x2,.,xn),
y
= (y1, y2, .,yn).
,
x
= (x1, x2,.,xn),
y
= (y1, y2, .,yn).
Vom nota in continuare: ps(x, y) = <x, y>= xy.
Norma vectorului x
este x
= ![]() =
=
![]() .
.
Spatiul Rn (Spatiul cu n dimensiuni). Structura algebrica
Produsul cartezian Rn = R R R, adica multimea:
Rn
formeaza o structura de spatiu vectorial peste corpul R, daca definim operatiile de adunare si inmultire cu scalari astfel:
(x1, x2, ..,xn) + (y1, y2, .,yn) = (x1 + y1, x2 + y2,., xn + yn),
unde
x =(x1, x2,.,xn),
y
= (y1, y2, .,yn),
x,
y ![]() Rn
Rn
si
a (x1, x2, .xn) = (ax1, ax2, ., axn),
unde
x =(x1, x2,.,xn)![]() Rn
, α
Rn
, α![]() R
.
R
.
Cazuri particulare
(i). n=1; R1 este multimea punctelor de pe dreapta reala R;
(ii). n=2; R2=este multimea punctelor din plan;
(iii). n=3; R3=este multimea punctelor din spatiu.
Definitia . O aplicatie ![]() ,
se numeste norma pe Rn
, daca satisface proprietatile:
,
se numeste norma pe Rn
, daca satisface proprietatile:
(i). ![]() ;
;
(ii). 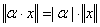 ,
(
,
(![]() )
)![]() ;
;
(iii). ![]() ,
(
,
(![]()
![]() .
.
Teorema . (a). Aplicatia ps : Rn Rn R, definita prin:
ps(x,
y)
= ![]() ,
x
= (x1, x2,.,xn),
y
= (y1, y2, .,yn),
,
x
= (x1, x2,.,xn),
y
= (y1, y2, .,yn),
este un produs scalar pe Rn .
(b).
Aplicata ![]() definita prin:
definita prin:
x
= ![]() =
=
![]() ,
x
,
x![]() ,
,
este o norma pe Rn .
Demonstratie. (a). Proprietatile (i)-(iv) ale produsului scalar se verifica imediat.
(b). De asemenea proprietatile (i)-(ii) ale normei rezulta imediat din proprietatile produsului scalar. Pentru demonstra cea de a treia proprietate de la norma, demonstram in prealabil doua inegalitati si anume:
(α). ![]() ;
;
(β). ![]() ;
(inegalitatea lui Schwarz);
;
(inegalitatea lui Schwarz);
(α). Din ![]() rezulta:
rezulta:
![]() .
.
(β). Daca ![]() atunci sau
atunci sau ![]() deci
deci
![]() ,
sau
,
sau ![]() deci
deci ![]() ;
in ambele cazuri ps(x, y) = 0, deci inegalitatea este
demonstrata.
;
in ambele cazuri ps(x, y) = 0, deci inegalitatea este
demonstrata.
Daca ![]() atunci
atunci ![]() ,
,
![]() si
si
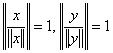 .
.
Notam ![]() si rezulta:
si rezulta:
![]() ,
,
adica
![]()
deci
![]() .
.
Folosind inegalitatea (β) rezulta imediat inegalitatea riunghiului:
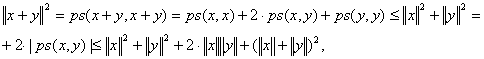
de unde:
![]() .
.
Definitia . Se numeste distanta (metrica) pe Rn, o aplicatie ![]() ,
care satisface proprietatile:
,
care satisface proprietatile:
(i). ![]() ;
;
(ii). ![]() ;
;
(iii). ![]() ;
(inegalitatea triunghiului).
;
(inegalitatea triunghiului).
Teorema . Aplicatia ![]() ,
definita prin:
,
definita prin:
![]()
este o distanta (metrica) pe Rn.
Definitia
. (i). Un spatiu vectorial pe care s-a definit o norma ![]() care satisface proprietatile (i), (ii), (iii) (de
la norma) se numeste spatiu vectorial
normat, sau mai scurt, spatiu normat.
care satisface proprietatile (i), (ii), (iii) (de
la norma) se numeste spatiu vectorial
normat, sau mai scurt, spatiu normat.
(ii). O multime X inzestrata cu o metrica
![]() ,
deci perechea
,
deci perechea ![]() ,
se numeste spatiu metric.
,
se numeste spatiu metric.
Observatie. Un spatiu normat este in acelasi timp si spatiu metric, cu metrica indusa de norma; exista insa si spatii metrice in care distanta (metrica) nu poate fi dedusa dintr-o norma.
Teorema
. Orice sistem de n vectori x1,
x2, ,xn ![]() Rn
;
xi = ,
Rn
;
xi = ,
i =1,2,.,n, cu proprietatea ca:
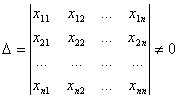 ,
,
formeaza o baza a lui Rn.
Demonstratie. Vectorii x1, x2,
,xn ![]() Rn
sunt liniar independenti deoarece
Rn
sunt liniar independenti deoarece
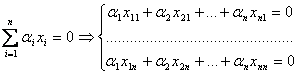 .
.
Sistemul de ecuatii liniare omogene (deoarece determinantul asociat
matricei coeficientilor este nenul) are solutia unica ![]() .
.
Deoarece ![]() rezulta de asemenea ca orice vector x
rezulta de asemenea ca orice vector x![]() Rn
se scrie, in mod unic, sub forma
Rn
se scrie, in mod unic, sub forma ![]() .
.
Observatie. Sistemul de vectori ![]() Rn
unde:
Rn
unde:
e1 =
e2 =
en =
formeaza o baza a spatiului Rn , numita baza canonica.
Operatii cu matrice partitionate
Ne situam de aceasta data in spatiul vectorial Mm,n(K) a matricelor cu m linii si n coloane peste corpul R (sau C).
Deseori este util sa se efectueze operatii cu matrice partitionate. Vom vedea avantajul partitionarii in special in cazul inversarii unei matrice prin partitionare, unde, in loc de a calcula inversa unei matrice de dimensiuni relativ mari, este suficient sa calculam inversele a doua matrice de dimensiuni mai mici.
Definitia . Se numeste partitionare a unei matrice A o impartire a matricei A in submatrice prin drepte orizontale si verticale.
Exemplu: Matricea A![]() Mm,n(K)
poate fi partitionata in submatricele:
Mm,n(K)
poate fi partitionata in submatricele:
A11![]() Mr,s(K),
A12
Mr,s(K),
A12![]() Mr,n-s(K),
A21
Mr,n-s(K),
A21![]() Mm-r,s(K),
A22
Mm-r,s(K),
A22![]() Mm-r,n-s(K);
Mm-r,n-s(K);
A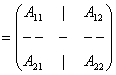 '
'
unde
A11
= , A12
=
, A12
=  ,
,
A21
=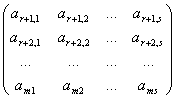 , A22 =
, A22 = 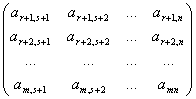 .
.
Adunarea prin partitionare a doua matrice de acelasi tip (de aceeasi dimensiune) si la fel partitionate, se realizeaza in mod obisnuit, interpretand submatricele ca si cum ar fi elemente ale matricei.
Fie matricea B![]() Mm,n(K),
de acelasi tip si partitionata la fel ca matricea A:
Mm,n(K),
de acelasi tip si partitionata la fel ca matricea A:
B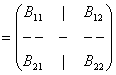 .
.
Atunci suma celor doua matrice este
matricea S![]() Mm,n(K),
Mm,n(K),
S = A + B 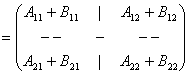 ,
,
S fiind partitionata analog cu matricele A si B.
Realizarea operatiei de inmultire a matricelor presupune partitionarea celor doua matrice conforma cerintelor inmultirii, adica diviziunile verticale ale primei matrices a fie aceleasi cu diviziunile orizontale ale celei de a doua matrice.
Se dau
matricele A![]() Mm,n(K),
B
Mm,n(K),
B![]() Mnp(K):
Mnp(K):
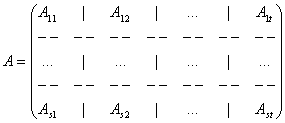
![]() m, cu
m, cu ![]() ;
;
![]()
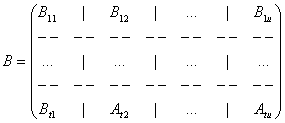
![]() n, cu
n, cu ![]() ;
;
![]()
atunci:
![]() .
.
Ne propunem acum sa determinam inversa unei matrice prin partitionare.
Fie A![]() M,n(R),
M,n(R),
![]()
A11![]() Mm(K),
A12
Mm(K),
A12![]() Mm,,n-m(K),
A21
Mm,,n-m(K),
A21![]() Mn,-m,m(K),
A22
Mn,-m,m(K),
A22![]() Mn-m,n-m(K);
Mn-m,n-m(K);
A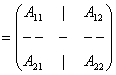 .
.
Presupunem ca ![]() si
determinam inversa A-1, necunoscuta,
partitionata la fel ca matricea A:
si
determinam inversa A-1, necunoscuta,
partitionata la fel ca matricea A:
A-1
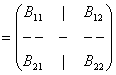 ,
,
din conditia ![]() .
.
Facand inmultirea prin partitionare rezulta:
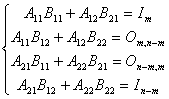
de unde rezulta:

si mai departe
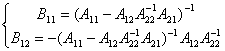
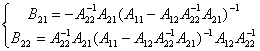 .
.
Cazuri particulare
(i). Calculati inversa matricei:
![]()
unde ![]() ,
,
![]() ,
,
![]() ,
,
![]() si α - aA-1b
si α - aA-1b![]() 0.
0.
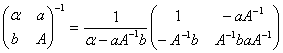
(ii). Calculati inversa matricei:
![]() ,
,
unde ![]() ,
,
![]() ,
,
![]() ,
,
![]() si α - bA-1a
si α - bA-1a![]() 0.
0.
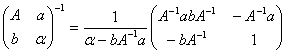 .
.
Structura topologica a spatiului Rn.
Definitia
. Fie n intervale pe dreapta
reala I1, I2,, In![]() R;
produsul lor cartezian
R;
produsul lor cartezian ![]() se
numeste interval n - dimensional;
se
numeste interval n - dimensional;
![]() .
.
Intervalele ![]() Mm,n(K)se numesc laturile intervalului n - dimensional.
Mm,n(K)se numesc laturile intervalului n - dimensional.
Definitia
. (i). O multime D![]() R este deschisa daca, sau este vida, sau daca nu este vida, atunci pentru
orice x
R este deschisa daca, sau este vida, sau daca nu este vida, atunci pentru
orice x![]() D
exista un r > , astfel incat
D
exista un r > , astfel incat ![]() .
.
(ii). Spunem ca V este o vecinatate a
punctului x![]() R, daca exista multimea deschisa D astfel incat x
R, daca exista multimea deschisa D astfel incat x![]() .
Notam cu V(x) multimea vecinatatilor lui x.
.
Notam cu V(x) multimea vecinatatilor lui x.
(iii).
Fie A![]() R
si x
R
si x![]() R.
Spunem ca x este un punct interior al multimii A, daca A
R.
Spunem ca x este un punct interior al multimii A, daca A![]() .
Multimea
.
Multimea  -
este punct interior al lui A}se
numeste interiorul multimii A.
-
este punct interior al lui A}se
numeste interiorul multimii A.
(iv). O
multime A![]() R se numeste inchisa
daca complementara sa este deschisa.
R se numeste inchisa
daca complementara sa este deschisa.
(v). Fie A![]() R
si x
R
si x![]() R.
Spunem ca x este punct aderent (respectiv punct
de acumulare) al multimii A, daca pentru orice V
R.
Spunem ca x este punct aderent (respectiv punct
de acumulare) al multimii A, daca pentru orice V![]() V(x),
are loc:
V(x),
are loc:
![]() ,
(respectiv
,
(respectiv ![]() ).
).
Multimile:
![]() este punct aderent al multimii A},
este punct aderent al multimii A},
respectiv
![]() este punct de acumulare al multimii A},
este punct de acumulare al multimii A},
se numesc aderenta sau inchiderea multimii A, respectiv multimea derivata a lui A.
Daca toate intervalele I1, I2,, In sunt deschise, atunci I se numeste interval
n dimensional deschis.
Daca toate intervalele I1, I2,, In sunt inchise, atunci I se numeste interval
n dimensional inchis.
Daca toate intervalele I1, I2,, In sunt marginite, atunci I se numeste interval
n dimensional marginit.
Exemple de intervale in Rn
In figura 1 sunt prezentate exemple de intervale din R2, in cazul a). deschise (linia intrerupta simbolizeaza faptul ca extremitatea respectiva nu apartine intervalului), b). Inchise (linia continua simbolizeaza faptul ca extremitatea respectiva apartine intervalului), c). marginite.
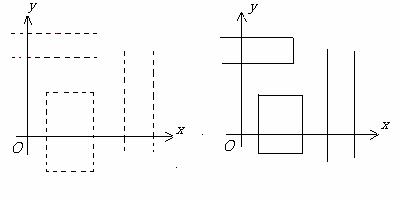
a). b).
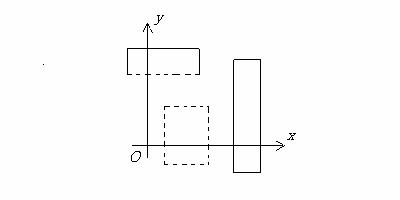
c).
Figura 1.
Definitia
. (i). Fie a![]() Rn
si r > 0. Se numeste sfera deschisa), cu centrul in a
si de raza r, multimea:
Rn
si r > 0. Se numeste sfera deschisa), cu centrul in a
si de raza r, multimea:
![]() .
.
(ii). Multimea:
![]()
se numeste sfera (inchisa), cu centrul in a si de raza r.
Cazuri particulare
(i). n = 1, R1 = R ![]() ,
deci sfera deschisa este un interval deschis cu centrul in a;
,
deci sfera deschisa este un interval deschis cu centrul in a;
(ii). n = 2, a = (a1, a2)![]() R2
,
R2
, ![]()
este cercul de centrul a si raza r.
In general cand vorbim de sfera subintelegem sfera deschisa.
Prezentam in continuare un rezultat care exprima faptul ca in Rn sfera de centrul a si raza r joaca acelasi rol ca intervalul n - dimensional care contine pe a.
Teorema . Orice sfera cu centrul in a contine un interval n - dimensional care contine pe a si reciproc, orice interval care contine pe a contine o sfera cu centrul in a.
Demonstratie. Fie ![]() o
sfera cu centrul in a si de raza r.
o
sfera cu centrul in a si de raza r.
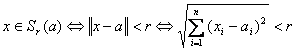 ,
,
unde x = (x1, x2, .,xn) si a = (a1, a2, .,an).
Consideram intervalele unidimensionale:
![]()
![]()
si intervalul n -
dimensional ![]() ,
,
![]() ;
;
![]() .
.
Aratam ca ![]() ;
;
![]()
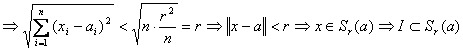
Reciproc, fie ![]() ,
interval n - dimensional care contine
pe a;
intervalul I contine un interval n - dimensional
,
interval n - dimensional care contine
pe a;
intervalul I contine un interval n - dimensional ![]() cu centrul in a si cu intervalele J1, J2,.,Jn
de aceeasi lungime:
cu centrul in a si cu intervalele J1, J2,.,Jn
de aceeasi lungime:
![]()
Aratam ca ![]() ,
de unde va rezulta ca
,
de unde va rezulta ca ![]() ;
;
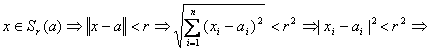
![]()
Concluzii cu privire la unele elemente de topologie in Rn:
(i). O vecinatate a unui punct a![]() Rn
este orice multime care contine o sfera
Rn
este orice multime care contine o sfera ![]() cu
centrul in a.
cu
centrul in a.
(ii). O multime ![]() este
vecinatate a unui punct a
este
vecinatate a unui punct a![]() Rn
, daca si numai daca exista un interval n
-dimensional I, astfel ca a
Rn
, daca si numai daca exista un interval n
-dimensional I, astfel ca a![]()
![]() .
.
(iii). O multime A![]() Rn
este marginita, daca exista o sfera, ( care poate fi presupusa cu centru in origine),
care contine pe A.
Rn
este marginita, daca exista o sfera, ( care poate fi presupusa cu centru in origine),
care contine pe A.
(iv). Multimile marginite si inchise din Rn se numesc multimi compacte.
Aplicatii.
Sa se studieze dependenta liniara pentru sistemele de vectori:
a). v1 = (2, 1, 3, 1), v2 = (1, 2, 0, 1), v3 = (-1, 1, -3, 0) in R4;
b). v1 = 8-t+7t2, v2 = 2-t+3t2, v3 = 1+t-3t2 in P2(t);
c). A1
= ![]() ,
A2 =
,
A2 = ![]() ,
A3 =
,
A3 = ![]() in M2,2(R).
in M2,2(R).
Sa se determine care dintre polinoamele t2 si t-1 apartin spatiului generat de
In R4 se dau vectorii v1 = (1, 1, 2, 1), v2 = (1, -1, 0, 1), v3 = (0, 0, -1, 1),
v4 = (1, 2, 2, 0). Sa se arate ca acestia formeaza o baza. Se cer coordonatele vectorului v = (1, 1, 1, 1) in aceasta baza.
In R5 sa se determine o baza a subspatiului vectorial generat de vectorii
v1 = (1, 2, -4, 3, 1), v2 = (2, 5, -3, 4, 8), v3 = (6, 17, -7, 10, 22),
v4 = (1, 3, -3, 2, 0).
Se dau vectorii a1 = (1, 0, 0), a2 = (2, 1, 0), a3 = (-3, 2, 1) si a = -8a1+4a2-a3, precum si vectorii b1 = a1 + a2 +a3, b2 = a1 + a2 - a3, b3 = a1 -a2 + a3. Sa se calculeze coordonatele vectorului a in baza .
Sa se determine vectorul normat v din R4 (de modul egal cu unitatea), ortogonal vectorilor v1 = (1, 1, 1, 1), v2 = (1, -1, -1, 1), v3 = (2, 1, 1, 3).
Sa se
arate ca functia ![]() prin
prin
<x,
y> = 3x1y1-x1y2-x2y1+2x1y2
, x
= (x1, x2), y
= (y1, y2)![]() ,
,
este un produs scalar.
Sa se arate ca urmatoarele multimi sunt subspatii vectoriale ale spatiilor vectoriale indicate:
a). ![]() ;
;
b). ![]() ;
;
c). D = ![]() , F
fiind multimea functiilor reale de variabila reala, diferentiabile.
, F
fiind multimea functiilor reale de variabila reala, diferentiabile.
9.
Sa se determine λ, μ![]() astfel
ca matricele
astfel
ca matricele
![]()
sa fie liniar independente.
Sa se construiasca o baza ortonormata
(adica o baza in care toti vectorii au modul egal cu unitatea si sunt doi cate
doi ortogonali) a spatiului R4 , presupunand ca doi
vectori ai bazei sunt v1 =
(![]() si
si
v2 = (![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2250
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved