| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
In cazul regresiei liniare, caz pe
care il vom studia in continuare, coeficientii ecuatiei de regresie in
esantion, a si b, sunt estimatii ale coeficientilor ecuatiei de regresie in
populatia generala a si b,
la fel cum media ![]() este estimator al mediei m.
In plus, acesti coeficienti au distributii de esantionare si, asa cum am vazut
in cursurile anterioare, in conditiile ipotezelor modelului de regresie
liniara, distributiile de esantionare ale parametrilor a si b au urmatoarele
proprietati:
este estimator al mediei m.
In plus, acesti coeficienti au distributii de esantionare si, asa cum am vazut
in cursurile anterioare, in conditiile ipotezelor modelului de regresie
liniara, distributiile de esantionare ale parametrilor a si b au urmatoarele
proprietati:
1. a si b sunt estimatori nedeplasati ai parametrilor a si b, adica ma a si mb b. Aceasta inseamna ca media estimatiilor este egala cu parametrul populatiei. Unele estimatii pot fi mai mici, altele pot fi mai mari, dar aceste deplasari nu sunt sistema-tice.
2. distributiile de esantionare ale
coeficientilor a si b sunt normal distribuite, cu mediile a
si b si dispersiile, respectiv, ![]() si
si
![]() .
.
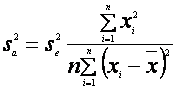
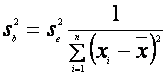
Ne reamintim ca: ![]()
iar eroarea standard a
estima-tiei (se) este: ![]()
unde se este estimatorul
abaterii medii patratice a rezidurilor (![]() ),
iar sa si sb sunt abaterile medii patratice pentru
coeficientii a si b.
),
iar sa si sb sunt abaterile medii patratice pentru
coeficientii a si b.
Parametrul b este de mare importanta pentru analiza statistica, deoarece el poate fi folosit in masurarea legaturii dintre variabila dependenta si cea independenta. Panta b masoara schimbarea variabilei rezultative care rezulta in urma modificarii cu o unitate a variabilei cauzale.
Astfel: m
(Y/X = xi) = ![]() = a bxi,
unde mYxi este media in populatia
generala a variabilei Y, cand variabila cauza ia valoarea xi. Daca b
= 0, inseamna ca linia de regresie este orizontala, adica
= a bxi,
unde mYxi este media in populatia
generala a variabilei Y, cand variabila cauza ia valoarea xi. Daca b
= 0, inseamna ca linia de regresie este orizontala, adica ![]() ,
atunci valoarea lui X nu este de nici un ajutor in previzionarea variabilei Y:
nu conteaza cat de mult se modifica X, deoarece nu implica nici o modificare in
Y (in medie).
,
atunci valoarea lui X nu este de nici un ajutor in previzionarea variabilei Y:
nu conteaza cat de mult se modifica X, deoarece nu implica nici o modificare in
Y (in medie).
Vom testa, prin urmare daca panta (b) este diferita de zero. Ipoteza nula (H0) va fi atunci aceea ca panta (b) este egala cu zero, cu ipoteza alternativa (H1) ca panta (b) este diferita de zero (pozitiva sau negativa, test bilateral):
H0 : b mb b
H1 : b ¹
Regiunea critica este data de z > za sau z < - za
Daca volumul esantionului este mare, vom utiliza testul z:
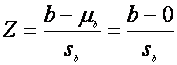
Pentru un prag de semnificatie a, vom respinge ipoteza nula (H0), cand z > za sau z < - za si vom concluziona ca este foarte improbabil ca estimatorul b sa provina dintr-o populatie cu b
Daca volumul esantionului este mic, vom utiliza testul t:
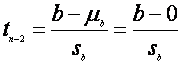
statistica ce urmeaza o distributie t cu (n - 2) grade de libertate.
Regiunea critica este data de
. | t | > ta/2, n-2 pentru test bilateral;
. t > ta, n-2 pentru test unila-teral dreapta;
. t < -ta, n-2 pentru test uni-lateral stanga
In cazul in care dorim sa testam ipoteza ca panta b este pozitiva, vom utiliza testul unilateral dreapta:
H0 : b
H1 : b > 0,
si vom respinge ipoteza nula daca t > ta, iar daca dorim sa tes-tam ipoteza ca panta b este negativa, vom utiliza test unilateral stanga:
H0 : b
H1 : b < 0,
si vom respinge ipoteza nula daca t < - ta, cu pragul de semnificatie a
Similar cu testarea ipotezei nule pentru b, putem utiliza un test t pentru parametrul a, cu ipotezele:
H0 : a
H1 : a ¹ 0 (sau H1 : a > 0 ori H1 : a < 0 in cazul testului unilateral) si statistica t:
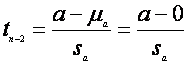
Cunoastem ca
patratul coeficientului de corelatie, calculat pentru un esantion (r2)
este egal cu coeficientul de determinatie (R2). Am vazut, de
asemenea, ca acest coeficient de corelatie (r) masoara intensitatea legaturii
dintre variabile. Daca R2 masoara proportia din variatia variabilei
dependente y, explicata de variatia variabilei independente x, deci are o
interpretare exacta, r poate fi folosit pentru a oferi o estimatie pe interval
de incredere a parametrului ![]() ,
coeficientul de corelatie din colectivitatea generala.
,
coeficientul de corelatie din colectivitatea generala.
Exista alte
circumstante in care suntem interesati doar in a afla daca exista intre
variabile o legatura liniara, nu si in masurarea relatiei de cauzalitate. In
unele cazuri, nu ne intereseaza nici macar sa identificam care variabila este
independenta si care este dependenta. Vom calcula atunci coeficientul de
corelatie (r) si pe baza distributiei sale de esantionare vom determina
intervalul de incredere pentru parametrul ![]() :
:
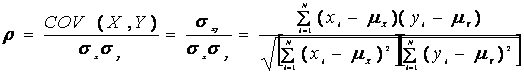
cu conditia ca cele doua variabile sa aiba o distributie bivariata normala.
Media estimatoare r este ![]() si abaterea medie patratica este
si abaterea medie patratica este 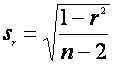 .
.
Semnificatia coeficientului de
corelatie (r) poate fi testata utilizand testul t. Se testeaza astfel daca ![]() ,
coeficientul de corelatie liniara in colectivitatea generala, intre doua
variabile, este semnificativ statistic diferit de zero. Ipoteza nula este:
,
coeficientul de corelatie liniara in colectivitatea generala, intre doua
variabile, este semnificativ statistic diferit de zero. Ipoteza nula este:
H0 : ![]() = 0, cu ipoteza alternativa: H1 :
= 0, cu ipoteza alternativa: H1 : ![]() ¹ 0 in cazul testului
bilateral si
¹ 0 in cazul testului
bilateral si ![]() > 0 sau
> 0 sau ![]() < 0 in cazul testului unilateral dreapta,
respectiv testul unilateral stanga.
< 0 in cazul testului unilateral dreapta,
respectiv testul unilateral stanga.
Statistica t este:
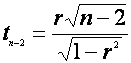
Se observa ca statistica t pentru
testarea ipotezei H0 : ![]() = 0 este
identica, de fapt, cu testul t pentru testarea ipotezei H0 : b pornind de la relatia:
= 0 este
identica, de fapt, cu testul t pentru testarea ipotezei H0 : b pornind de la relatia: ![]() .
Ipoteza nula se respinge daca valoarea calculata tn2 este mai mare
decat valoarea tabelata ta/2,n2 pentru testul bilateral si
tcalc. >ta,n2 sau tcalc. <
-ta,n2 pentru testul unilateral
dreapta, respectiv, stanga.
.
Ipoteza nula se respinge daca valoarea calculata tn2 este mai mare
decat valoarea tabelata ta/2,n2 pentru testul bilateral si
tcalc. >ta,n2 sau tcalc. <
-ta,n2 pentru testul unilateral
dreapta, respectiv, stanga.
Exemplu
Sa presupunem ca pe baza analizei statistice a n=20 de cazuri individuale s-a stabilit ca exista o legatura liniara directa intre numarul turistilor cazati intr-un hotel si incasarile realizate de un Internet Caf situat in apropiere, legatura a carei intensitate s-a masurat prin coeficientul de corelatie r=0,52.
Vom testa semnificatia coeficientului de corelatie astfel:
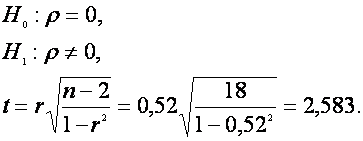
Pentru o
probabilitate de ![]()
![]()
Putem
concluziona, cum ![]() ,
ca avem suficiente dovezi pentru a respinge ipoteza nula si a accepta ipoteza
alternativa, aceea ca
,
ca avem suficiente dovezi pentru a respinge ipoteza nula si a accepta ipoteza
alternativa, aceea ca ![]() este semnificativ diferit de zero.
este semnificativ diferit de zero.
Trebuie sa subliniem ca testul t se poate utiliza cu succes si pentru testarea semnificatiei coeficientului de corelatie a rangurilor Spearman, rs, cu cateva conditii. Astfel, acest coeficient este de fapt un coeficient de corelatie (r, numit si Pearson), calculat nu pentru valori efective, ci pentru ranguri.
Atunci ipotezele de testat sunt:
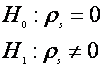 (se poate dezvolta si test unilateral).
(se poate dezvolta si test unilateral).
Cand n>30, rs este
aproximativ normal distribuit, cu media 0 si abatere medie patratica ![]() .
Atunci, pentru n>30 testul statistic este:
.
Atunci, pentru n>30 testul statistic este:
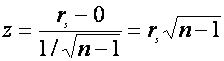 (distribuit normal standard).
(distribuit normal standard).
Regiunea critica este data de ![]() sau
sau ![]() (si se adapteaza pentru testul unilateral).
(si se adapteaza pentru testul unilateral).
Una dintre utilizarile importante ale analizei regresiei simple liniare este sa obtinem previzionari (sau predictii) ale variabilei dependente, conditionate de valorile variabilei independente, adica sa obtinem previzionari conditionate. Daca presupunem ca variabila independenta ia valoarea specificata Xn+1 si legatura liniara se mentine, atunci valoarea corespunzatoare a variabilei dependente Yn+1 este:
Yn+1,i = a bXn+1,i + en+1,I
cu media:
m (Yn+1/X = Xn+1) = a bXn+1.
Cu alte cuvinte, ecuatiile de mai sus sunt utilizate pentru estimarea mediei de raspuns si pentru estimarea unui raspuns individual. Pentru amandoua estimatiile putem obtine estimatii punctuale sau pe intervale de incredere. Pentru a obtine estimatii punctuale, folosim ecuatia de regresie liniara in esantion:
yi = a + bxi + ei
si atunci, inlocuind cu valoarea data Xn+1, obtinem:
![]() = a + b xn+1.
= a + b xn+1.
Construirea intervalului de
incredere pentru previzionare necesita cunoasterea distributiei, mediei si
dispersiei pentru ![]() .
Variabila
.
Variabila ![]() urmeaza o distributie t cu (n - 2) grade de
libertate. Dispersia asociata variabilei poate fi identificata in trei cazuri
si anume:
urmeaza o distributie t cu (n - 2) grade de
libertate. Dispersia asociata variabilei poate fi identificata in trei cazuri
si anume:
Stim ca:
![]()
daca xn+1 = ![]() ,
atunci
,
atunci ![]() iar estimatorul dispersiei pentru
iar estimatorul dispersiei pentru ![]() este
este
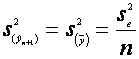
Intervalul de incredere este, in acest caz:
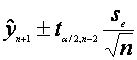
In acest caz:
![]()
iar estimatorul dispersiei pentru ![]() este:
este:

Intervalul de incredere pentru media de raspuns este:
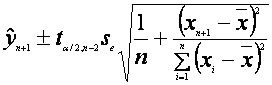
. determinarea intervalului de incredere pentru un raspuns individual
In acest caz trebuie sa determinam
dispersia diferentei 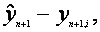 adica dispersia erorii de previzionare. Dispersia in esantion este:
adica dispersia erorii de previzionare. Dispersia in esantion este:
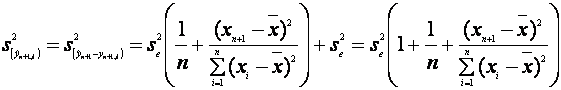
Intervalul de incredere este:
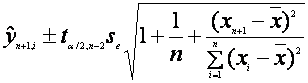
Exemplu
Proprietarul unui minihotel dezvolta o analiza statistica pentru determinarea cheltuielilor cu materialele de curatenie (y) in functie de numarul camerelor ocupate (x). El determina ecuatia de regresie pentru cheltuielile zilnice (pentru detergent, clor etc.) (zeci mii lei), pe baza datelor inregistrate pentru n=14 zile:
![]()
![]()
![]()
![]()
a) Proprietarul doreste sa estimeze cheltuielile pentru o zi in care are 6 camere ocupate;
b) Proprietarul doreste sa estimeze cheltuielile medii pentru zilele in care are 6 camere ocupate.
Daca numarul
camerelor ocupate este ![]() ,
atunci:
,
atunci:
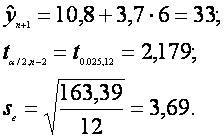
a) Intervalul de incredere pentru cheltuielile unei zile in care sunt 6 camere ocupate este:
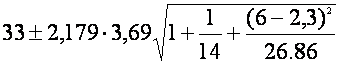
adica (22,89;43,11) garantat cu o probabilitate de 95%;
b) Intervalul de incredere pentru media cheltuielilor zilnice in cazul in care au 6 camere ocupate este:
![]()
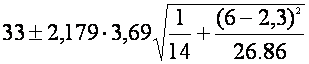
adica (30,19;35,82), garantat cu o probabilitate de 95%.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3723
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved