| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Teoria informatiei raspunde la doua probleme fundamentale din teoria comunicatiilor.
limita
- compresia datelor - ![]()
![]()
limita - rata
transmisiei datelor - ![]()
O sursa de
informatii discreta X de alfabet finit ![]() si cardinalitate
si cardinalitate ![]() ,
,
![]() conform unei distributii de probabilitate
conform unei distributii de probabilitate ![]() .
.
Sursa poate fi modelata matematic ca o variabila aleatoare X avand
acelasi alfabet ![]() si aceeasi functie de distributie a
probabilitatilor:
si aceeasi functie de distributie a
probabilitatilor:
![]()
unde
![]() si
si ![]()
Emiterea
unui simbol de catre sursa este echivalenta cu realizarea unui eveniment
constand din faptul ca sursa X emite simbolul xi, respectiv variabila aleatoare X ia valoarea xi cu probabilitatea ![]() .
Daca asociem alfabetului sursei X campul complet de evenimente, evenimentul xi reprezinta emiterea de
catre sursa X a simbolului xi
cu probabilitatea pi.
.
Daca asociem alfabetului sursei X campul complet de evenimente, evenimentul xi reprezinta emiterea de
catre sursa X a simbolului xi
cu probabilitatea pi.
Valoarea informatiei obtinuta prin realizarea evenimentului xi depinde numai probabilitatea cu care are loc evenimentul.
Shannon a definit
cantitatea de informatie obtinuta
prin observarea evenimentului ![]() prin functia logaritmica:
prin functia logaritmica:
![]()
Informatia proprie i(xi) reprezinta o masura a informatiei obtinute prin realizarea evenimentuluui xi sau echivalent o masura a incertitudinii anulate de realizarea evenimentului xi.
Evenimentul sigur nu produce informatie:
![]() ;
;
Informatia proprie are valoare pozitiva:
![]() ;
;
Observatie:
folosim conventia ![]() deoarece
deoarece ![]() .
.
Realizarea evenimentului xi prin care v.a. X ia valoarea xi este cu atat mai incerta cu cat probabilitatea p(xi) are o valoare mai mica:
![]() .
.
Informatia este aditiva. Fie doua
evenimente independente, ![]() si
si ![]() ,
ce au loc cu probabilitatile individuale
,
ce au loc cu probabilitatile individuale![]() si
si ![]() .
Informatia obtinuta prin realizarea celor doua evenimente egaleaza suma
informatiilor obtinute prin realizarea fiecarui eveniment in parte:
.
Informatia obtinuta prin realizarea celor doua evenimente egaleaza suma
informatiilor obtinute prin realizarea fiecarui eveniment in parte:
![]() .
.
Consideram:

Consideram: (distributie uniforma)


Deci 16 elemente pot fi descrise distinct de 4 biti.
Entropia Shannon a v.a. ![]() este definita de valoarea medie a informatiei
proprii:
este definita de valoarea medie a informatiei
proprii:
![]()
respectiv:
![]() , [biti].
, [biti].
Pentru v.a. discreta X, notand
f.m.p. ![]() ,
entropia
,
entropia ![]() poate fi exprimata prin relatia:
poate fi exprimata prin relatia:
![]() , [biti].
, [biti].
Entropia binara reprezinta entropia unei v.a. avand doua realizari posibile.
Fie alfabetul
binar ![]() si notam
si notam ![]() si
si ![]() pentru
pentru ![]() .
Entropia binara notata
.
Entropia binara notata ![]() este:
este:
![]() ,
,
si este reprezentata in fig. 1.
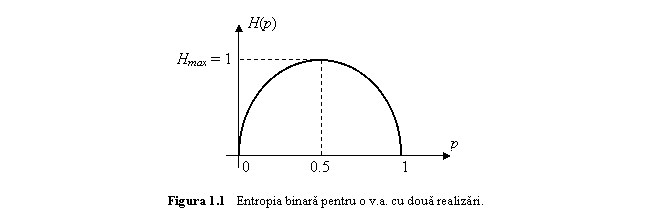

Graficul entropiei binare ilustreaza urmatoarele proprietati:
![]() , cu precizarea
, cu precizarea ![]() daca
daca ![]() sau
sau ![]() ;
;
![]()
![]()
![]() este o functie strict concava in raport cu p.
este o functie strict concava in raport cu p.
entropia este o functie continua de probabilitatile simbolurilor sursei
entropia este simetrica (are aceleasi valori indiferent cum sunt ordonate probabilitatile simbolurilor sursei)
entropia este aditiva
valoarea
entropiei este intotdeauna pozitiva ![]()
![]()
![]()
![]() daca si numai daca X are distributie p(X) uniforma
pe alfabetul
daca si numai daca X are distributie p(X) uniforma
pe alfabetul![]() (simbolurile
sunt egal probabile)
(simbolurile
sunt egal probabile)
Pentru simboluri egal probabile: ![]() mare
mare![]() mare.
mare.
entropia este o functie concava in raport cu probabilitatea p
Din acesti parametrii se poate construi un model probabilistic al sursei de informatie si se pot defini
Entropia sursei ![]()
Entropia maxima a sursei:
Debitul de informatie ![]() ,
,
Durata medie a unui simbol ![]()
Redundanta sursei ![]()
In realitate dependenta probabilistica a simbolurilor dintr-o secventa si probabilitatile inegale de aparitie a simbolurilor reduc valoarea reala a lui H(X).
Pentru
doua v.a. discrete X si Y, de alfabet X si Y,
caracterizate de distributia reunita a probabilitatilor ![]() entropia reunita:
entropia reunita:
![]()
masoara
incertitudinea totala asociata perechii de v.a. ![]() ,
reprezentand valoarea medie a informatiei ce caracterizeaza perechea de v.a.
,
reprezentand valoarea medie a informatiei ce caracterizeaza perechea de v.a.
Pentru
aceeasi pereche de v.a. X, Y, entropia conditionata ![]() reprezinta cantitatea de incertitudine ramasa
asupra variabilei X dupa observarea
variabilei Y:
reprezinta cantitatea de incertitudine ramasa
asupra variabilei X dupa observarea
variabilei Y:
![]()
Folosind
relatia intre distributia de probabilitati reunite ![]() a perechii de v.a. X si Y, distributia
marginala
a perechii de v.a. X si Y, distributia
marginala ![]() si distributia conditionata
si distributia conditionata ![]() :
:
![]()
vom putea exprima entropia variabilei X conditionata de cunoasterea variabilei Y prin:
![]() .
.
Entropia
conditionata ![]() poate fi interpretata ca fiind cantitatea
medie de informatie pe care X o
contine, dupa ce Y este cunoscut. Astfel,
definim:
poate fi interpretata ca fiind cantitatea
medie de informatie pe care X o
contine, dupa ce Y este cunoscut. Astfel,
definim:
![]() ,
pentru y astfel incat
,
pentru y astfel incat ![]() .
.
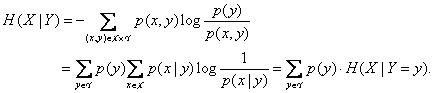
Acum, ![]() este chiar media tuturor entropiilor
este chiar media tuturor entropiilor ![]() ale
v.a. X, pentru orice
ale
v.a. X, pentru orice ![]() fixat.
fixat.
Similar, entropia v.a. Y conditionata de cunoasterea variabilei X se defineste prin:
![]()
Proprietatile entropiilor reunite si entropiilor conditionate
Entropiile reunite sunt comutative:
![]()
Entropia unei v.a. este mai mica decat entropia reunita a doua v.a:
![]()
cu egalitate daca:
![]()
Subaditivitatea
Pentru o pereche de
v.a. ![]() , entropia reunita este mai mica sau cel
mult egala cu suma entropiilor celor doua variabile:
, entropia reunita este mai mica sau cel
mult egala cu suma entropiilor celor doua variabile:
![]() ,
,
cu egalitate daca si numai daca X, Y sunt v.a. independente.
* Subaditivatate puternica:
![]()
cu ![]() daca si numai daca
daca si numai daca ![]() lant
Markov
lant
Markov
Entropiile conditionate sunt pozitive:
![]()
Conditionarea reduce entropia:
![]() cu egalitate daca X si Y sunt independente.
(2 v.a.)
cu egalitate daca X si Y sunt independente.
(2 v.a.)
![]() (3 v.a.)
(3 v.a.)
Fiind dat un
spatiu masurabil pe care se definesc doua masuri probabilistice reprezentate de
doua distributii de probabilitate ![]() si
si ![]() ,
,
![]() apartinand aceleiasi multimi, entropia
relativa este o masura a "distantei"
dintre cele doua distributii.
apartinand aceleiasi multimi, entropia
relativa este o masura a "distantei"
dintre cele doua distributii.
Denumita si
distanta KL (Kullback Leibler), entropia relativa se defineste in raport cu
perechea de distributii ![]() si
si ![]() prin:
prin:
![]()
cu respectarea conventiilor:
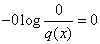 si
si ![]() ,
pentru
,
pentru ![]() .
.
Proprietatile entropiei relative:
![]()
cu egalitate daca si numai daca p(x) = q(x) pentru orice x.
Demonstratie:
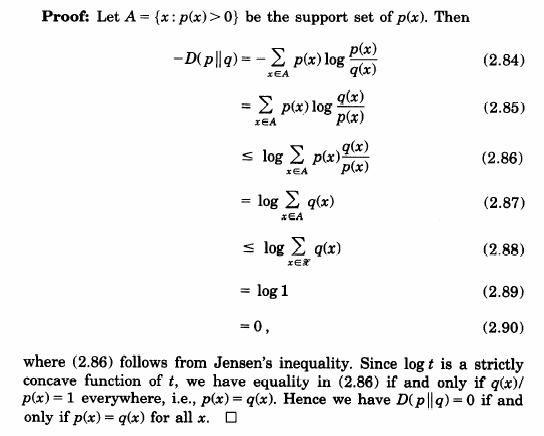

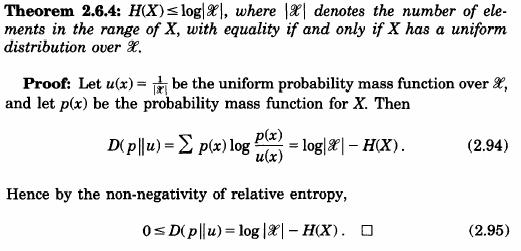
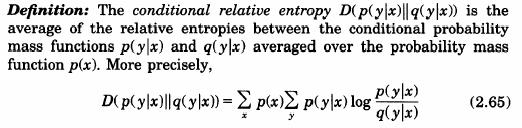

![]() .
.

Pentru
perechea de v.a. X, Y de alfabet X Y si
distributie reunita ![]() ,
informatia mutuala
,
informatia mutuala ![]() reprezinta cantitatea de informatie pe care
cele doua variabile o au in comun. Luate separat, cele doua variabile sunt
caracterizate de entropiile
reprezinta cantitatea de informatie pe care
cele doua variabile o au in comun. Luate separat, cele doua variabile sunt
caracterizate de entropiile ![]() ,
,
![]() si de entropia reunita
si de entropia reunita ![]() ,
deci informatia mutuala va fi data de relatia:
,
deci informatia mutuala va fi data de relatia:
![]()
Informatia mutuala poate fi exprimata in termenii entropiilor conditionate prin putand fi interpretata ca reducerea incertitudinii asupra v.a. X cand se cunoaste v.a. Y:
![]()
Demonstratie:
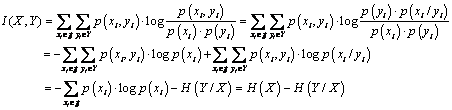
In mod similar se poate scrie si relatia simetrica: ![]() .
.
Pentru o
pereche de doua variabile identice ![]() ,
informatia mutuala egaleaza entropia variabilei X:
,
informatia mutuala egaleaza entropia variabilei X:
![]()
Pentru
o pereche de v.a. X si Y de alfabet X Y,
depinzand de v.a. Z, de alfabet Z, informatia
mutuala conditionata ![]() este data de relatia:
este data de relatia:
![]()
si reprezinta cantitatea de informatie "continuta" in v.a. X, datorita cunoasterii v.a. Y cand v.a. Z este data (cunoscuta).
Conditionarea reduce entropia si vom putea scrie pentru cele trei v.a. X, Y si Z:
![]() sau
sau
![]()
cu egalitate ![]() X, Y si Z
sunt independente.
X, Y si Z
sunt independente.
Pentru trei v.a., intuitiv, ne asteptam ca incertitudinea despre X, cand stim valoarea v.a. Y si Z este mai mica decat incertitudinea cand stim doar pe Y. Cu ajutorul definitiilor, afirmatia "conditionarea reduce entropia" este echivalenta cu:
![]()
adica o forma rearanjata a inegalitatii de subaditivitate puternica.
Proprietatile informatiei mutuale
Informatia mutuala este comutativa:
![]()
Informatia mutuala este pozitiva:
![]()
cu egalitate daca si numai daca X si Y sunt v.a. independente.
Informatia mutuala este marginita superior:
![]() sau
sau ![]() ,
,
cu egalitate ![]() X
este o functie de Y,
X
este o functie de Y,![]() ,
respectiv Y este o functie de X,
,
respectiv Y este o functie de X, ![]() .
.
Informatia mutuala nu este intotdeauna subaditiva:
![]()
Informatia mutuala nu este intotdeauna superaditiva:
![]()
Relatiile
intre entropiile ![]() ,
,
![]() ,
entropia reunita
,
entropia reunita ![]() ,
entropiile conditionate
,
entropiile conditionate ![]() ,
,
![]() si informatia
mutuala
si informatia
mutuala ![]() pot fi ilustrate prin diagrama Venn.
pot fi ilustrate prin diagrama Venn.
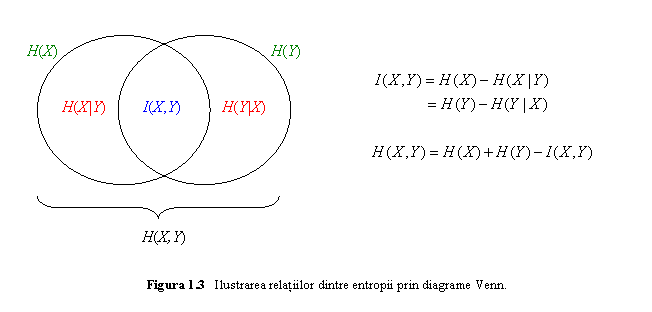

Tinand cont de relatia intre entropia reunita si entropiile conditionate:
![]()
Demonstratie
Formula trebiue corectata >>>
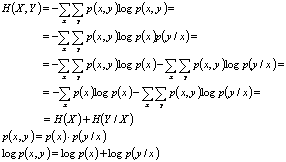
Regula lantului pentru trei variabile aleatoare X, Y, Z:
![]()
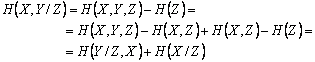
![]()
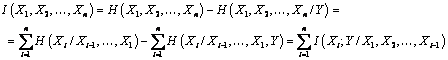
din curs tti2
Daca X, Y, Z formeaza un lant Markov, ( X Y Z ) atunci
H(X) ³ I(X,Y) ³ I(X,Z)
Prima inegalitate este indeplinita cu semnul "=" daca si numai daca fiind dat Y este posibila reconstructia lui X.
Daca o v.a. X este afectata de zgomot rezultand v.a. Y atunci "procesarea datelor" nu poate fi folosita pentru a creste cantitatea de informatie mutuala intre semnalul observat Y si informatia initiala X.
Deci, H(X) ³ I(X,Y
A doua inegalitate, I(X,Y) ³ I(X,Z) este echivalenta cu H(X | Y) £ H(X | Z)
Deoarece X Y Z formeaza un lant Markov, Z Y X este deasemenea un lant Markov si in consecinta aplicand inegalitatea subaditivitatii puternice rezulta
H(X,Y,Z) - H(Y,Z) = H(X | Y, Z) £ H(X|Z) = H(X,Z) - H(Z)
Presupunem I(X,Y) < H(X). In acest caz nu ar mai fi posibil sa-l reconstruim pe X din Y deoarece daca Z este o incercare de reconstructie bazata numai pe cunoasterea lui Y, atunci X Y Z trebuie sa fie un lant Markov si
H(X) ³ I(X,Z) conform inegalitatii procesarii datelor. Deci Z ¹ X
Daca I(X,Y) = H(X) atunci H(X | Y) = 0 si ori decate ori p(X = x, Y = y) > 0 vom avea p(X = x | Y = y) = 1, altfel spus daca Y = y atunci, prin inferenta, cu certitudine X = x, permitand astfel reconstructia lui X.
din curs tti2
Daca X Y Z este un lant Markov, la fel este si Z Y X si in consecinta, ca un corolar la inegalitatea procesarii datelor vom avea
I(Z,Y) ³ I(Z,X)
Aceasta inegalitate se numeste data pipeline inequality si ne spune in mod intuitiv ca informatia pe care Z o are in comun cu X este informatia pe care Z o are in comun cu Y, deci informatia este "pipelined" de la X prin Y catre Z.
Din curs tti 1
Inegalitatea procesarii datelor reprezinta o inegalitate fundamentala in teoria informatiei, bazata pe ideea reprezentarii secventei de simboluri generate de sursa ca un lant Markov de variabile aleatoare X1, X2, ,Xn pentru care putem scrie:
![]()
![]()
Daca variabila
aleatoare X1 este afectata de zgomot actiunile de procesare a
datelor nu permit cresterea cantitatii de informatie mutuala intre Xi, ![]() si informatia originala X1.
si informatia originala X1.
Daca ![]() formeaza un lant Markov, atunci si
formeaza un lant Markov, atunci si ![]() formeaza un lant Markov si
formeaza un lant Markov si![]()
Informatia pe care X3 o imparte cu X1 trebuie sa fie cel putin aceeasi cu care X3 o imparte cu X2.
Pentru un lant Markov, X1, X2, X3, ., Xn, rata entropiei este data de relatia
![]() ,
,
unde entropia conditionata este calculata folosind distributia stationara cunoscuta.
Daca avem o secventa de n variabile aleatoare, se pune intrebarea naturala "Cum creste entropia secventei cu n?". Definim rata entropiei ca acea rata de crestere ca in cele ce urmeaza.
Definitia 1: Rata entropiei unui proces aleator X(t) = X1, X2, .Xn reprezinta entropia per simbol a n variabile aleatoare si este definita prin
![]()
cand limita exista.
Vom considera cateva exemple simple de procese aleatoare si rata entropiei corespunzatoare.
Exemplul 1: Fie X1, X2, ., Xn variabile aleatoare i.i.d. Atunci :
![]()
Exemplul 2: Secvente de variabile aleatoare distribuite independent dar nu si identice. In acest caz,
![]()
dar valorile H(Xi) nu sunt toate egale.
Definitia 2: In termenii entropiei conditionate H(Xn | Xn-1, Xn-2, ., X1) rata entropiei se poate defini prin
![]()
cand aceasta limita exista.
(Demonstrarea existentei limitei H'(X) :)
Teorema 1: Pentru un proces aleator stationar, entropia conditionata ca caracterizeaza secventa indexata de v.a. X1, X2, ., Xn notata H(Xn | Xn-1, Xn-2, ., X1) scade cu n si are limita data de rata entropiei H'(X).
Demonstratie:
![]() (3)
(3)
![]() , (4)
, (4)
unde inegalitatea rezulta deoarece conditionarea reduce entropia si egalitatea din stationaritatea procesului.
Intrucat H(Xn | Xn-1, Xn-2, ., X1) este o secventa descrescatoare de numere pozitive, aceasta are o limita, care este H'(X).
Teorema 2: Pentru un proces aleator stationar, limitele din relatiile (1) si (2) exista si sunt egale,
![]()
Demonstratie: Din legea lantului Markov, avem
![]()
de exemplu, rata entropiei este media in timp a entropiilor conditionate.
Conform teoremei 1, entropiile conditionate tind la o limita H'(X) si in consecinta:
![]()
Pentru orice proces stationar ergodic are loc (cu probabilitate 1) relatia
![]()
Aceasta arata semnificatia ratei entropiei ca o descriere a "lungimii medii" respectiv a numarului mediu de biti pe simbol ce caracterizeaza o secventa de n variabile aleatoare reprezentand un proces stationar ergodic.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2781
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved