| CATEGORII DOCUMENTE | ||
|
||
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Hmota a energie
1 Hmotnost pohybujících se těles
Zopakujme si nejprve některé důležité vztahy z klasické mechaniky. Nejprve několik důležitých vztahů pro mechaniku jedné částice.
Impuls síly I vyjadřuje časový účinek síly. Působí-li na částici konstantní síla po dobu τ = t – t je impuls síly dán součinem této síly a času:
![]() (1)
(1)
Impuls síly je tedy roven změně hybnosti částice.
Je-li síla časově proměnná, je impuls síly definován jako integrál
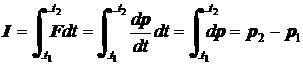 . (2)
. (2)
Impuls
síly měříme ve stejných jednotkách jako hybnost 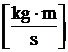 .
.
Práce A vyjadřuje dráhový účinek síly. Působí-li na dráze s podél trajektorie na částici konstantní síla, bude práce dána součinem velikosti síly a dráhy:
![]() . (3)
. (3)
(Výraz ![]() znamená
průměrnou rychlost.)
znamená
průměrnou rychlost.)
Veličinu
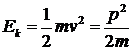 , (4)
, (4)
nazveme kinetickou energií částice. Vidíme, že práce síly působící na částici podél dráhy je rovna změně kinetické energie částice. Je-li síla časově proměnná a míří-li pod obecným úhlem k tečnému vektoru trajektorie (obr. 1), definujeme práci jako integrál.
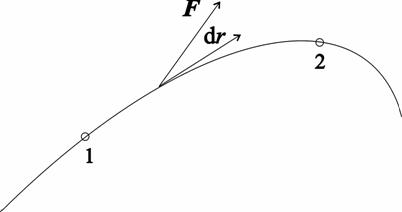
Obr. 1
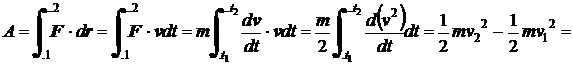
![]() . (5)
. (5)
Práce a
kinetická energie jsou tedy dvě fyzikální veličiny, které mají
v soustavě SI fyzikální rozměr L MT a měří se v jednotkách 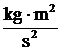 , které souhrnně nazýváme Joule (J). Kinetická energie
popisuje určitý stav částice, nazýváme jí tedy veličinou
stavovou. Naopak práce charakterizuje
určitý proces neboli přechod
z jednoho stavu do druhého.
, které souhrnně nazýváme Joule (J). Kinetická energie
popisuje určitý stav částice, nazýváme jí tedy veličinou
stavovou. Naopak práce charakterizuje
určitý proces neboli přechod
z jednoho stavu do druhého.
Výkon N je práce za jednotku času. Vycházíme-li ze vztahu dA = F dr, můžeme ho definovat jako
![]() . (6)
. (6)
Výkon
má rozměr L MT-3 a měří se
v jednotkách 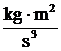 nazývaných watt (W).
nazývaných watt (W).
Dále budeme potřebovat malou a exkurzi do mechaniky soustavy částic.
První věta impulsová:
Celková změna hybnosti soustavy částic je rovna výslednici vnějších sil.
Matematicky vyjádřeno:
![]() , (7)
, (7)
kde P značí hybnost celé soustavy částic a F(e) výslednici externích sil. Vnitřní síly se podle zákona akce a reakce vyruší, takže i když ovlivňují vnitřní pohyb jednotlivých částic, na hybnosti soustavy jako celku nic nezmění.
Je-li soustava izolovaná, je výslednice vnějších sil
nulová, ![]() a platí zákon
zachování hybnosti izolované soustavy částic:
a platí zákon
zachování hybnosti izolované soustavy částic:
P = konst; (8)
Celková hybnost soustavy se zachovává.
Rovnici (1.66.) lze pojímat jako rovnici, kterou se řídí pohyb jediného hmotného bodu reprezentující celou soustavu. Tímto myšleným hmotným bodem je hmotný střed soustavy, jemuž přisoudíme hmotnost M celé soustavy, a rychlost V která reprezentuje součet rychlostí všech bodů soustavy. Pro hybnost hmotného středu pak platí:
![]() ,
, ![]() . (9)
. (9)
Ve vztažné soustavě spojené s hmotným středem (těžištěm) je rychlost hmotného středu nulová, a tedy celková hybnost soustavy hmotných bodů je v ní rovna nule. ( P´ = 0 ). ( Přesně vzato hmotný střed soustavy a její těžiště nejsou totožné, například v nehomogenním tíhovém poli se liší. Přesto však je v teoretické fyzice zvykem nazývat soustavu hmotného středu těžišťovou.)
V izolované soustavě částic je výslednice vnějších sil nulová, takže rychlost těžiště zůstává konstantní:
V = konst. (10)
Což praví další zákon zachování rychlosti těžiště izolované soustavy. Jedná se v podstatě o zobecnění zákona setrvačnosti jedné částice pro soustavu částic.
Druhá věta impulsová je o momentu hybnosti soustavy částic:
Moment hybnosti hmotného bodu ke zvolenému bodu O, je definován jako vektorový součin polohového vektoru r vedeného z bodu O a hybnosti p hmotného bodu.
![]() (11)
(11)
Moment hybnosti je tedy pseudovektor. Celkový moment hybnosti soustavy hmotných bodů se rovná vektorovému součtu momentů hybnosti všech bodů soustavy, které jsou určeny k témuž zvolenému bodu O.
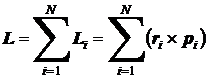 (12)
(12)
Časová změna celkového momentu hybnosti L soustavy hmotných bodů je rovna výslednému momentu vnějších sil N(e)
![]()
Moment hybnosti i
moment vnějších sil se přitom vztahuje k témuž bodu, k
počátku soustavy souřadnic. Je-li soustava izolovaná, je výsledný
moment vnějších sil nulový, ![]() a platí zákon zachování
celkového momentu hybnosti izolované soustavy částic:
a platí zákon zachování
celkového momentu hybnosti izolované soustavy částic:
L = konst. ; (14)
Celkový moment hybnosti izolované soustavy částic se zachovává.
Proveďme nyní další z našich myšlenkových pokusů. Přenesme se na raketu, která se bude vůči naší laboratorní soustavě Σ pohybovat rychlostí v=(vx,0,0). V počátku O´ soustavy Σ´ (na lodi) je stlačená pružina se závažím o hmotnosti m a zajištěná tak, aby se v určený okamžik dala odjistit a mohla začít působit silou na závaží. Váhu samotné pružiny neuvažujeme. Mechanismus pružiny je natočen tak, aby síla, kterou bude působit, byla kolmá k ose x´, například ve směru osy y´. Dále si musíme uvědomit, že síla žádného péra není časově neměnná a že absolutní hodnota rychlosti závaží vůči soustavě Σ bude po určité době aktivního působení pružiny větší než rychlost rakety. (Pokud tedy ovšem nebude raketa lehčí než ono závaží.) Z těchto dvou důvodů budeme uvažovat dráhu v soustavě Σ´ co nejkratší, nejlépe dy´ a čas také dt . Pozorujme nyní, co se stane ,když v domluvený okamžik ( t = t´ = 0 ) pružinu odjistíme. Pozorovatel v raketě nezjistí nic zvláštního:
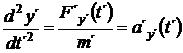 . (15)
. (15)
V nekonečně kratičkém okamžiku dt můžeme sílu považovat za konstantní a rovnici 15 můžeme zapsat jednodušeji
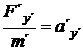 , (16)
, (16)
přesně podle druhého Newtonova zákona. Avšak pozorovatel v klidové (někdy se používá výraz laboratorní) soustavě Σ uvidí následující: Čas v raketě plyne 1/γ krát pomaleji, a proto i silové působení je pro pozorovatele v soustavě Σ 1/γ krát menší než v raketě. Z toho vyplývá, že:
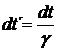 (17)
(17)
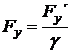 (18)
(18)
Co se děje se zrychlením?
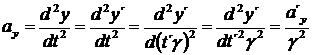 , (19)
, (19)
Tento vztah jsme již odvodili dříve, viz rovnice (1.36).
Nyní nám zbývá určit hmotnost, což je snadné:
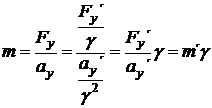 (20)
(20)
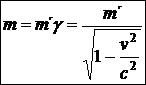 (21)
(21)
Veličina m´ se někdy nazývá klidovou hmotností a značí se m . Vyjadřuje, jakou by mělo těleso hmotnost, kdyby bylo vůči laboratorní soustavě Σ v klidu. Vidíme, že m je větší než m´ a limitně se blíží k nekonečnu při rychlosti blížící se rychlosti světla. To znamená, že rychlost světla je pro hmotná tělesa nedosažitelná. Přesněji, pro tělesa, která mají klidovou hmotnost rozdílnou od nuly.
Zatím jsme tuto hmotnost posuzovali pouze jako vlastnost, která brání změně hybnosti tělesa, tedy jako hmotnost setrvačnou. Zkusme se podívat, co se bude dít s hmotností, která je zodpovědná za gravitační interakci, při velké rychlosti. (Obě hmotnosti, jak setrvačná, tak gravitační, jsou mezinárodně označovány pojmem masa, odtud m . ) Nechť se soustava Σ´ pohybuje rovnoměrně přímočaře rychlostí v=(vx,0,0) v homogenním gravitačním poli, jehož siločáry jsou kolmé k vektoru rychlosti v. Soustava Σ´ (uvažujme pro změnu například vagón, a nemysleme na to, že by se mu asi brzy odpařila kola) má pevnou podlahu, na níž je umístěno pokusné zařízení. Bude podobné kulečníkovému stolu, který nebude stát na čtyřech nohách, ale na kulovitém velmi vratkém postavci podpírajícím stůl přesně uprostřed. Připomeňme ještě, že stůl je vyroben z mimořádně lehkého materiálu, a má proto zanedbatelnou hmotnost. Viz obr 2, kde je horní polovině obrázku zobrazen vagón ze strany a ve spodní polovině obrázku z ptačí perspektivy.
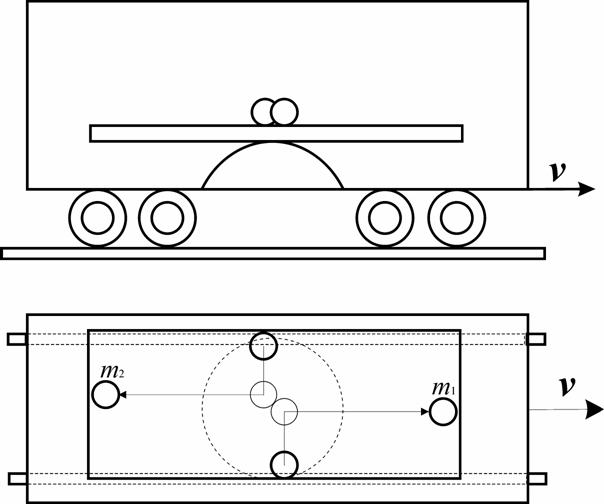
Obr. 2
Díky těmto vlastnostem je stůl mimořádně citlivý na síly, které na něho působí. Nyní přistoupíme k experimentu. Dvě stejně těžké koule o hmotnosti m a m odpálíme proti sobě od bočních stěn stolu stejnou rychlostí u tak, aby po dokonale pružné srážce pokračovaly rovnoběžně se směrem rychlosti v. Je zřejmé, že do srážky je stůl dokonale vyvážen, takže se ani nehne. Koule jsou stejně těžké a v každém okamžiku symetricky vzdálené od středu, takže těžiště soustavy leží stále přesně na vrcholu kulové podložky. Rychlost těžiště je tedy ve vagónu nulová a z pohledu pozorovatele v stojící soustavě Σ mají koule sice zvětšenou hmotnost, ale obě stejně, takže těžiště má rychlost v a zůstává také na kulovém vrchlíku, viz. (10). Podívejme se, co se děje po srážce.
a) Ve vagónu: Koule o sebe plesknou a vzdalují se od sebe stejnými rychlostmi opačného směru a jejich hmotnosti jsou stejné, takže těžiště se ani nehne a stůl je stále dokonale vyvážen.
b) Z pohledu pozorovatele v klidné soustavě Σ: Rychlost koule 1, která se odrazila rovnoběžně souhlasně s vektorem rychlosti v, bude podle (1.25.)
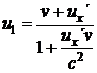 , (22)
, (22)
a rychlost druhé koule bude
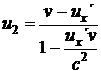 . (23)
. (23)
Tyto dva vztahy říkají, že první koule (která je po srážce víc ve předu) se bude od středu stolu vzdalovat pomaleji než před srážkou (druhá naopak rychleji), a tím pádem by těžiště stolu mělo zpomalit. Znamená to, že stůl by se měl po určité době převrátit, ale jen z pohledu pozorovatele v klidové soustavě Σ, což je značně podezřelé. Zkusme se podívat, jestli změněné hmotnosti obou koulí po srážce tento deficit náhodou nevyrovnají. Upravme nejdříve vzorec (21.) za pomocí vztahu (2):
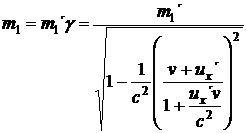 =
(24)
=
(24)
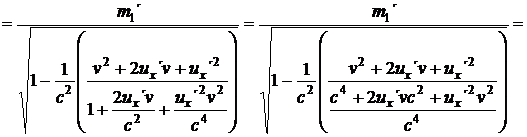
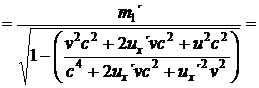
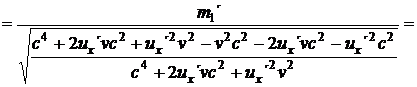
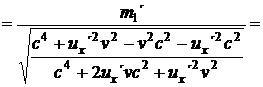
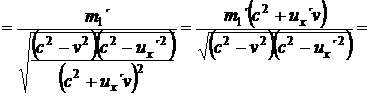
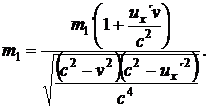 (25)
(25)
Hmotnost druhé koule bude analogicky dána vztahem:
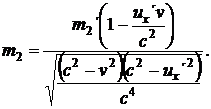 (26)
(26)
Vidíme, že výraz ve jmenovateli je v obou případech stejný, stejné jsou i klidové hmotnosti m m ´. Rovnice (25.) a (26.) se liší pouze výrazem v závorce v čitateli. Využijeme toho a označíme si hmotnosti m a m pracovně jako
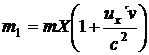 (27)
(27)
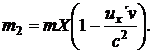 (28)
(28)
Kde veličina
mX je rovna 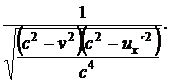
Podle (9.) a (10.) musí platit
P =MV = (m + m ) V m u + m u . (29)
Dosadíme-li nyní za m , m , u a u z rovnic (27), (28), (22) a (23), dostaneme:
![]()
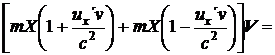
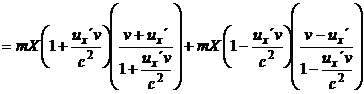 . (30)
. (30)
Zástupná veličina mX se na obou stranách vykrátí a na první pohled se zjednoduší také pravá strana
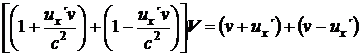 , (31)
, (31)
Takže nakonec z toho zbude
![]() . (32)
. (32)
Rychlost těžiště zůstává díky zvětšené gravitační hmotnosti první koule (a zmenšené u druhé) stále stejná a díky tomu zůstává stůl stále dokonale vyvážen i pro pozorovatele z klidové soustavy Σ. Vidíme, že s rychlostí tělesa roste nejenom setrvačná hmotnost, která brání jeho urychlování, ale i jeho tíha v gravitačním poli.!
Otázkou je, jak bude vypadat síla působící rovnoběžně s vektorem rychlosti v. Pokusme se na ni odpovědět. Vyjdeme z klasického vztahu pro sílu a hybnost:
![]() (33)
(33)
Pro hybnost při velkých rychlostech ovšem použijeme
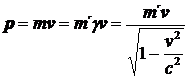 . (34)
. (34)
Síla tedy bude
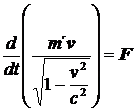 . (35)
. (35)
Derivací levé strany (35), kdy v je funkcí času (t), dostaneme:
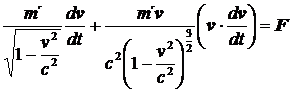 (36)
(36)
Uvážíme nyní dva případy, kdy síla působí rovnoběžně nebo kolmo k rychlosti v. V prvním případě, kdy F || v , můžeme libovolný vektor rychlosti ve výrazu (36.) nahradit jeho absolutní hodnotou, platí:
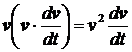
a z (36.) dostáváme:
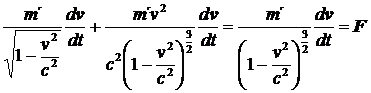 . (37)
. (37)
V druhém případě, kdy F ┴ v , platí:
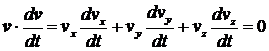
a z (36.) dostáváme:
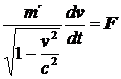 (38)
(38)
Neboli:
![]() (39)
(39)
![]() (40)
(40)
Dosadíme-li nyní za ax a ay vztahy (1.35.) a (1.36.), obdržíme následující:
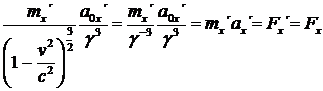 (41)
(41)
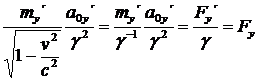 (42)
(42)
V souvislosti
s vektorem síly, se hmotnosti ![]() někdy říká
podélná hmotnost a hmotnosti
někdy říká
podélná hmotnost a hmotnosti ![]() příčná hmotnost.
Pozoruhodné je, že síla rovnoběžná s rychlostí v má stejnou velikost
v obou soustavách, čehož nyní využijeme.
příčná hmotnost.
Pozoruhodné je, že síla rovnoběžná s rychlostí v má stejnou velikost
v obou soustavách, čehož nyní využijeme.
2 Energie pohybujících se těles
Vyjděme z rovnice (5.). Práce vynaložená na změnu hybnosti tělesa je rovna rozdílu jeho kinetické energie před a po urychlení. Nejprve určíme nekonečně malý přírůstek dEk
![]()
![]() . (43)
. (43)
Budeme-li sčítat nekonečně malé přírůstky dEk a budeme-li přitom mít na paměti, že hmotnost roste podle vztahu (21.),
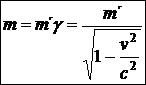 (21)
(21)
vyjde nám pro kinetickou energii integrál od počáteční nulové rychlosti do libovolné hodnoty v :
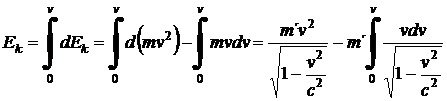 . (44)
. (44)
Neurčitý integrál
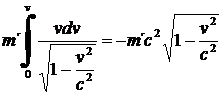 . (45)
. (45)
Kinetická energie je tedy po dosazení rychlostí v = 0 a v = v do (45.):
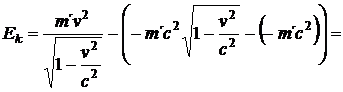
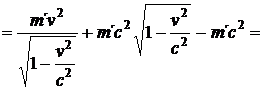
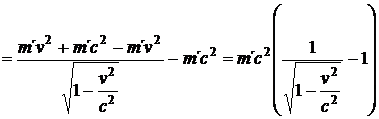 (46)
(46)
Vezmeme-li v úvahu (21.), můžeme konečný výsledek zapsat ve tvaru:
![]() . (47)
. (47)
Kinetickou energii Ek můžeme chápat jako rozdíl dvou energií,
energie celkové ![]() (48)
(48)
a energie klidové ![]() . (49)
. (49)
Klidová energie je energie, která je ukryta v tělese, i když je vzhledem k dané inerciální soustavě v klidu.
Vypočteme ještě rozdíl:
![]() (50)
(50)
Protože m´ i c se při přechodu z jedné inerciální soustavy do druhé nemění, je tento výraz invariantní vůči Lorentzově transformaci. Mělo by tedy platit:
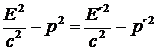 (51)
(51)
Vraťme se ještě na chvíli k rovnici
Tentýž výsledek dostaneme za pomoci vzorce pro vzdálenost (1.6) a rychlosti (1.55); aspoň je trochu prověříme.
Práce se musí rovnat součinu síly a vzdálenosti.
![]() (52)
(52)
Dle (1.6) a (41.) jsou si vzdálenost a síla rovny
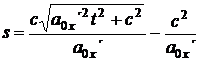 (53)
(53)
![]() . (41)
. (41)
Práce potom bude:
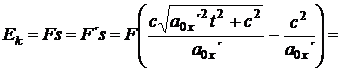
![]() (54)
(54)
Z rovnice pro rychlost (1.55.) dále vypočteme
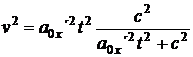 (55)
(55)
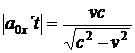 (56)
(56)
a dosadíme do (54.).
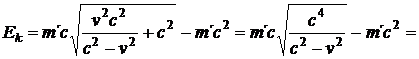
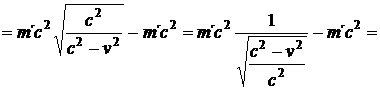
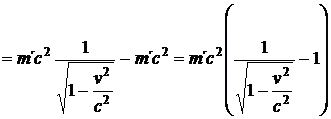 (46)
(46)
3 Absolutno nebo relativita?
Až doposud jsme odvozovali naši teorii na základě zpomalování času v letící inerciální soustavě Σ´ vůči naší laboratorní, tj. klidové a také inerciální, soustavě Σ. V obou soustavách probíhali všechny fyzikální děje naprosto stejně, takže je nešlo od sebe odlišit podle dějů v nich probíhajících. Otázkou stále zůstává, která z těchto soustav je vlastně ta klidová. Až doposud jsme si vybírali libovolnou inerciální soustavu jako tu klidovou Σ a nějakou jinou, vůči ní se pohybující, za tu, ve které se vůči té klidové zpomaluje čas. Existuje nějaká inerciální klidová soustava, vůči níž jsou všechny ostatní pohybující se soustavy ty, ve kterých se zpomaluje čas? Je zřejmé, že pozorovatel v raketě, která se pohybuje inerciálně, by na základě pokusů se světlem došel k naprosto stejným výsledkům jako pozorovatel v „klidové“ soustavě a že by tedy mohl klidně prohlásit, že soustava Σ ´ spojená s raketou je klidová laboratorní a že v soustavě Σ plyne čas pomaleji. Tento výsledek by však byl v rozporu se závěry, které by odvodil pozorovatel v soustavě Σ. Kdo má tedy pravdu? Nebo snad mají pravdu oba? Zpomalení času je pouze relativní? Zpomaluje se čas v soustavě Σ ´ vůči soustavě Σ a zároveň v soustavě Σ vůči soustavě Σ´ ? Neexistuje absolutně klidná soustava neboli elektromagnetický éter? Pokusme se odpovědět na tuto otázku. Nejdřív však malé upozornění.
4 Intermezzo
Až doposud jsem ve výkladu postupoval podle oficiálních učebnic, ze kterých čerpají informace studenti na konci středních škol a na začátku vysokoškolského studia. Některá odvození jsem si musel vymyslet sám, aby výklad byl ucelený a aby si čtenář nemusel některé věci domýšlet, hledat jinde nebo aby dokonce některým tvrzení nebyl nucen pouze věřit. Kapitoly 1. a tedy nejsou v rozporu s oficiálním názorem na teorii relativity, který je studentům předkládán „ke strávení“. Následující text se bude od všeobecně uznávaných názorů na toto téma v některých místech lišit, takže považuji za svou povinnost na tuto skutečnost dopředu upozornit, aby ovlivnění touto knížkou nebylo důvodem střetu názorů mezi zkoušejícím a studentem s patřičnými důsledky. Pro ty, které oficiální stanovisko neuspokojuje, je určen další text.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1372
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
Distribuie URL
Adauga cod HTML in site