| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
ČÍSELNÉ RADY A ICH VLASTNOSTI
Definícia:
Nech je daná postupnosť ![]() . Postupnosť
. Postupnosť ![]() , kde
, kde ![]() , sa nazýva postupnosť
čiastočných súčtov postupnosti
, sa nazýva postupnosť
čiastočných súčtov postupnosti ![]() . Ak existuje
. Ak existuje ![]() , potom
, potom ![]() nazveme súčtom radu
nazveme súčtom radu ![]() a povieme, že rad
a povieme, že rad ![]() je konvergentný.
je konvergentný.
Ak je však ![]() divergentný, nazývame rad
divergentný, nazývame rad ![]() divergentným. Ak
je
divergentným. Ak
je ![]() hovoríme, že rad diverguje
k
hovoríme, že rad diverguje
k ![]() .
.
Príklad
a)
Rad ![]() diverguje k
diverguje k ![]() , pretože
, pretože
![]() .
.
b)
Rad ![]() diverguje k
diverguje k ![]() , pretože
, pretože
![]()
c)
Rad ![]() diverguje (v tomto
prípade sa tiež hovorí, že osciluje), pretože súčty tvorí postupnosť
diverguje (v tomto
prípade sa tiež hovorí, že osciluje), pretože súčty tvorí postupnosť ![]() , ktorá nemá limitu.
, ktorá nemá limitu.
Príklad
Uvažujme
o geometrickom rade ![]() . Pre
. Pre ![]() je postupnosť
čiastočných súčtov daná vzťahom:
je postupnosť
čiastočných súčtov daná vzťahom: ![]() .
.
a)
Ak je ![]() , potom
, potom ![]() , rad diverguje k
, rad diverguje k ![]() :
:
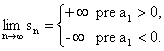
b)
Ak je ![]() , potom
, potom ![]() , rad konverguje.
, rad konverguje.
c)
Ak je ![]() , potom
, potom ![]() neexistuje a rad
diverguje.
neexistuje a rad
diverguje.
Príklad
Uvažujme
o rade ![]() .
.
Pretože platí: ![]() ,
,
je ![]() ,
,
potom ![]() , rad konverguje.
, rad konverguje.
Príklad
Rad ![]() konverguje, lebo jeho
súčet je rovný 0
konverguje, lebo jeho
súčet je rovný 0 ![]() . Ak však vynecháme zátvorky, získame rad divergentný:
. Ak však vynecháme zátvorky, získame rad divergentný:
![]()
Alebo naopak, pridaním vhodných zátvoriek sme z divergentného radu získali rad konvergentný.
Nasledujúca veta
hovorí, že súčet radu sa pridaním zátvoriek nezmení, ak je rad
konvergentný alebo či diverguje k ![]() .
.
Veta:
Nech ![]() , kde
, kde ![]() môže byť aj
môže byť aj ![]() alebo
alebo ![]() , a
, a ![]() je rastúca postupnosť prirodzených čísel. Potom je:
je rastúca postupnosť prirodzených čísel. Potom je:
![]() .
.
Veta:
Nech ![]() sú konvergentné rady,
sú konvergentné rady, ![]() . Potom je:
. Potom je:
![]() .
.
Nutná podmienka konvergencie radu:
Veta:
Keď rad ![]() konverguje, je
konverguje, je ![]() .
.
Dôkaz
Označme ![]() . Pretože rad konverguje, existuje vlastná limita
. Pretože rad konverguje, existuje vlastná limita ![]() . Pretože
. Pretože ![]() .
.
Pozor, veta hovorí, že z konvergencie radu vyplýva nulová limita postupnosti jej členov, avšak z nulovej limity obecne nevyplýva konvergencia radu!
Príklad
Uvažujme
o tzv. harmonickom rade ![]() .
.
Uvažujme takto:

Vybraná
postupnosť ![]() z postupnosti
čiastočných súčtov
z postupnosti
čiastočných súčtov ![]() diverguje k
diverguje k ![]() .
.
Pretože
postupnosť ![]() je rastúca,
je rastúca, ![]() , jej limita existuje, a to konečná alebo
, jej limita existuje, a to konečná alebo ![]() a je rovná limite akejkoľvek vybranej postupnosti.
a je rovná limite akejkoľvek vybranej postupnosti.
Teda: ![]() .
.
Harmonický rad ![]() teda diverguje k
teda diverguje k ![]() , aj keď je
, aj keď je ![]() .
.
Rady s nezápornými členmi
Veta:
Keď existuje ![]() také, že pre všetky
také, že pre všetky ![]() platí nerovnosť
platí nerovnosť ![]() , potom
, potom
z konvergencie radu ![]() vyplýva konvergencia
vyplýva konvergencia ![]() ,
,
z divergencie radu ![]() vyplýva divergencia
vyplýva divergencia ![]() .
.
Veta:
Nech ![]() a
a![]() sú rady s nezápornými členmi.
sú rady s nezápornými členmi.
Potom platí:
Keď existuje konečná
limita ![]() , potom z konvergencie radu
, potom z konvergencie radu ![]() vyplýva konvergencia
vyplýva konvergencia ![]() .
.
Keď existuje (konečná
alebo nekonečná) nenulová limita ![]() , potom z divergencie radu
, potom z divergencie radu ![]() vyplýva divergencia
vyplýva divergencia ![]() .
.
Keď existuje konečná
nenulová limita ![]() , potom rady
, potom rady ![]() a
a![]() súčasne konvergujú alebo divergujú.
súčasne konvergujú alebo divergujú.
Veta:
Keď existuje ![]() také, že pre všetky
také, že pre všetky ![]() je
je ![]() , potom rada
, potom rada ![]() konverguje.
konverguje.
Avšak pre každé ![]() existuje
existuje ![]() také, že
také, že ![]() , potom rada
, potom rada ![]() diverguje.
diverguje.
Veta:
Cauchyho limitné odmocninové kritérium
Nech ![]() a
a ![]() . Ak je
. Ak je ![]() , rada
, rada ![]() konverguje, ak je
konverguje, ak je ![]() , rada
, rada ![]() diverguje.
diverguje.
Veta:
d`Alembertovo podielové kritérium
Nech je ![]() . Keď existuje
. Keď existuje ![]() také, že pre všetky
také, že pre všetky ![]() je
je ![]() , potom rada
, potom rada ![]() konverguje.
konverguje.
Keď existuje ![]() také, že pre všetky
také, že pre všetky ![]() je
je ![]() , tak rada
, tak rada ![]() diverguje.
diverguje.
Veta:
d`Alembertovo limitné podielové kritérium
Nech ![]() a existuje
a existuje ![]() . Ak je
. Ak je ![]() ,
, ![]() konverguje, ak je
konverguje, ak je ![]() ,
, ![]() diverguje.
diverguje.
Veta:
Raabeho kritérium
Nech ![]() a existuje
a existuje 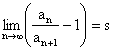 . Ak je
. Ak je ![]() , rada
, rada ![]() konverguje, ak je však
konverguje, ak je však ![]() , rada
, rada ![]() diverguje.
diverguje.
Alternujúce rady
Veta:
Leibnizovo kritérium pre alternujúce rady
Nech ![]() je monotónna postupnosť,
pre ktorú platí
je monotónna postupnosť,
pre ktorú platí ![]() . Potom rada
. Potom rada ![]() je konvergujúca.
je konvergujúca.
Príklad
Podľa
Leibnizovho kritéria konverguje napríklad rada ![]() .
.
Veta:
Ak konverguje rada ![]() , konverguje aj
, konverguje aj ![]() .
.
Definícia:
Ak je konvergentná
rada ![]() , nazýva sa rada
, nazýva sa rada ![]() absolútne konvergentná.
absolútne konvergentná.
Ak je však rada ![]() konvergentná a rada
konvergentná a rada ![]() divergentná, nazýva sa
rada
divergentná, nazýva sa
rada ![]() neabsolútne
konvergujúca.
neabsolútne
konvergujúca.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2221
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved