| CATEGORII DOCUMENTE | ||
|
||
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
A DIFFERENT DEMONSTRATION OF
THE PYTHAGOREAN THEOREM USING THE POWER OF THE POINT WITH RESPECT TO
In the present paper I will give / offer you not only a different demonstration of the Pythagorean Theorem but also some demonstrations of other important theorems in geometry (The Height Theorem, The Catheters Theorem and The Generalized Pythagorean Theorem), using The Power of the Point with Respect to a Circle.
I would also like to add that these demonstrations are completely different from those already known.
THE
POWER OF A POINT WITH RESPECT TO
In this section I will point out / bring to mind what the power of a point with respect to a circle is.
STATEMENT 1. Any point P inside a circle and chord AB which contains this point, the product
PA ∙ PB is constant.
Demonstration. Given
a point P inside a circle of centre O and ray / radius R and the variable chord
AB, so that P ![]() (AB). We build / draw a chord CD through point
P, see figure above.
(AB). We build / draw a chord CD through point
P, see figure above.
Angles ![]()
![]() and
and
![]() have equal measures with half measure of the arc
have equal measures with half measure of the arc
![]() ,
we obtain
,
we obtain
![]() (1)
(1)
Angles APC and BPD being vertically opposed angles, are congruent.
![]() (2)
(2)
From
(1) and (2), we obtain: ![]() ,
,
we obtain / get the proportion ![]() ,
which is equivalent to the
,
which is equivalent to the
statement ![]() .
.
The constant value of
the product ![]() multiplied by (-1) is called the power of an
internal point P with respect to the circle.
multiplied by (-1) is called the power of an
internal point P with respect to the circle.
STATEMENT
2.
Any point P outside a circle and the secant which contains this point and
intersects the circle in points A and B (A![]() (PB)),
the product
(PB)),
the product
![]() is constant.
is constant.
Demonstration. Given a point P outside the circle of centre O and ray / radius R and the secant PA which intersect the circle in A and B. We build a secant PC through point P, which intersects the circle in C and D, see figure above.
From
m(![]() )
+ m(
)
+ m(![]() )
=
)
= ![]()
and
m(![]() )
+ m(
)
+ m(![]() )
=
)
= ![]() ,
,
we deduce that
m(![]() )
= m(
)
= m(![]() ),
resulting in
),
resulting in
![]()
We have
![]() and
and
![]() ,
, ![]()
![]()
From the similarity of the two triangles we obtain the proposition:
![]()
i.e. ![]() .
.
The constant value of
the product ![]() is called the power of an external point P
with respect to the circle.
is called the power of an external point P
with respect to the circle.
Obs. If / As ![]() ,
then the straight line P is tangent to the circle and
,
then the straight line P is tangent to the circle and
![]() becomes
becomes
![]()
2. THE PYTHAGOREAN THEOREM
If in a triangle ABC,
right angled in A, then ![]() .
.
Demonstration. We
consider the triangle ABC a right-angled one, inscribed in the circle with the
center O and radius R. Through O, the middle of the hypotenuse BC, we draw the
parallel line OD for AB, D![]() (AC)
which intersects the circle in the points E and F; D
(AC)
which intersects the circle in the points E and F; D![]() (OE).
As [OD] is a midline in the triangle ABC, we deduce that
(OE).
As [OD] is a midline in the triangle ABC, we deduce that ![]() .
Considering the power of the interior point D towards the circle, we have DA.
.
Considering the power of the interior point D towards the circle, we have DA. ![]() ,
resulting that
,
resulting that ![]() (1)
(1)
Taking into account that
![]() and that
and that ![]() ,
the equality (1) becomes
,
the equality (1) becomes 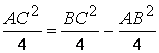 ,
and we obtain
,
and we obtain ![]() .
.
* This demonstration is different from the ones we know and it appeared for the first time in the magazine Scoala Valceana The Mathematics notebook of the students in Valcea edited by The School Inspectorate of Valcea County, The Society for Mathematical Sciences Rm. Valcea subsidiary, Teachers Assembly house in Valcea, year 19
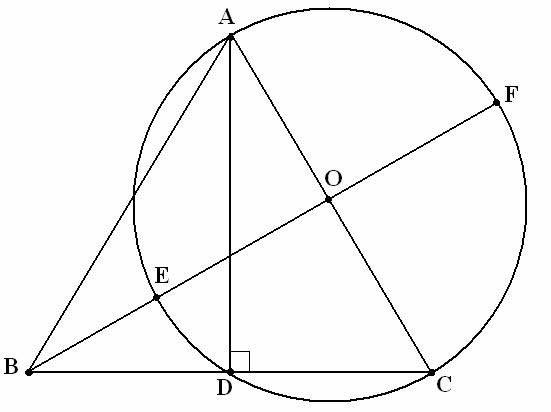
THE RECIPROCAL PYTHAGOREAN THEOREM
If we have ![]() in a triangle ABC, then the angle A is a right
one.
in a triangle ABC, then the angle A is a right
one.
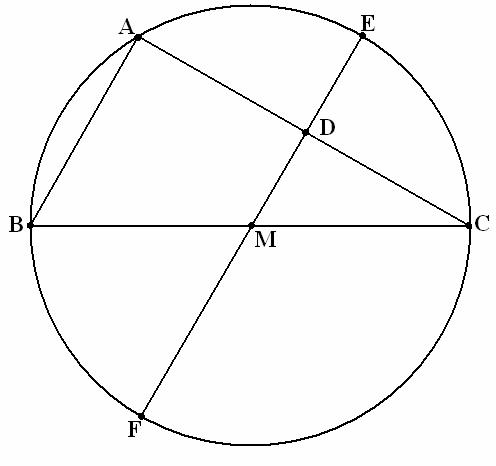
Demonstration. We
consider the triangle ABC in which ![]() ,
inscribed in the circle with the center O and radius R. Through M, the middle
of the side BC, we draw the parallel line MD for AB,
,
inscribed in the circle with the center O and radius R. Through M, the middle
of the side BC, we draw the parallel line MD for AB, ![]() which intersects the circle in E and F;
which intersects the circle in E and F; ![]() .
As [MD] is midline in the triangle ABC, we deduce that
.
As [MD] is midline in the triangle ABC, we deduce that ![]() .
Considering the power of the interior points M and D towards the circle, we
have
.
Considering the power of the interior points M and D towards the circle, we
have ![]() (1) and
(1) and ![]() respectively (2).
respectively (2).
The equality no. (2) becomes ![]() ,
resulting in
,
resulting in 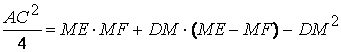 (3)
(3)
Taking into account that
![]() ,
the equality no. (3) turns into
,
the equality no. (3) turns into 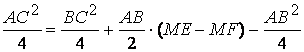
then in ![]() . (4)
. (4)
From ![]() and (4) we get
and (4) we get ![]() and (1) leads to
and (1) leads to ![]() .
.
From ![]() and the fact that the points E, B, C belong to
the circle with the center O and radius R, we deduce that the point M is
identical with the center O and that [BC] is the diameter of the circle, which
means that
and the fact that the points E, B, C belong to
the circle with the center O and radius R, we deduce that the point M is
identical with the center O and that [BC] is the diameter of the circle, which
means that 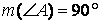 ,
that is the triangle ABC is right-angled in A.
,
that is the triangle ABC is right-angled in A.
THE ALTITUDE THEOREM
If [AD] is the altitude
within the triangle ABC which is right-angled in A, then ![]() .
.

Demonstration. The
triangle ABV which is right-angled in A is inscribed in the circle with the
center O and diameter BC. We draw ![]() ,
,
![]() and note as E the point of the intersection
between the straight line AD and the circle; see the figure! As [BC] is a
diameter perpendicular to the chord AE in the point D, we deduce that
and note as E the point of the intersection
between the straight line AD and the circle; see the figure! As [BC] is a
diameter perpendicular to the chord AE in the point D, we deduce that ![]() .
According to the power of the interior point D towards the circle, we have
.
According to the power of the interior point D towards the circle, we have ![]() (2)
(2)
Taking (1) into account,
the equality (2) becomes ![]() .
.
THE CATHETUS THEOREM
If in the triangle ABC
which is right-angled in A, ![]() A, then
A, then ![]() .
.
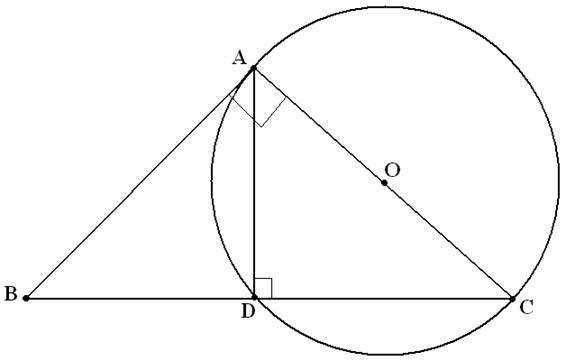
Demonstration. The
triangle ABC being right-angled in A is inscribed in the circle with the center
O and diameter AC; ![]() .
As the triangle ABC is right-angled in A, the straight line BA is tangent to
the circle in the point A. According to the power of the point B which is
external to the circle, we have
.
As the triangle ABC is right-angled in A, the straight line BA is tangent to
the circle in the point A. According to the power of the point B which is
external to the circle, we have ![]() ,
that is
,
that is ![]() .
.
Notice In parallel, it
shall be demonstrated that![]() .
.
PYTHAGOREAN THEOREM GENERALISED
I. If the triangle ABC
has the acute angle B and ![]() A,
then
A,
then ![]() .
.
Demonstration. The
triangle ADC being right-angled in D is inscribed in the circle with the center
O and diameter AC; ![]() The straight line BO intersects the circle in
the points E and F;
The straight line BO intersects the circle in
the points E and F; ![]() ;
see the figure!
;
see the figure!
According to the power
of the point B which is external to the circle, we have ![]() ,
resulting in
,
resulting in ![]() ,
which turns into
,
which turns into ![]() ,
then into
,
then into
![]() (1)
(1)
As [BO] is a median line
in the triangle ABC and its length is given by ![]() ,
then the equality no. (1) becomes
,
then the equality no. (1) becomes
![]() ,
,
leading us to ![]() .
.
II. If the triangle ABC
has the obtuse angle B and ![]() A,
then
A,
then ![]()
Demonstration. The
triangle ABD being right-angled in D is inscribed in the circle with the center
O and diameter AB; ![]() .
The straight line CO intersects the circle in the points E and F;
.
The straight line CO intersects the circle in the points E and F; ![]() ;
see the figure!
;
see the figure!
According to the power of the point C which is external to the
circle, we have ![]() ,
leading to
,
leading to ![]() ,
that is
,
that is  (1)
(1)
Knowing that [CO] is a
median line in the triangle ABC and its length is given by ![]() ,
the equality no.(1) becomes
,
the equality no.(1) becomes
![]() ,
,
resulting in
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1291
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved