| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Plane and Space linear geometry
In this chapter we will study the quadratic variations of an euclidian punctual space E = (E3, V3, φ ) starting from different ways of geometrical determination . The variations of the dimension, one respective two of a quadratical space E are affinity own subspace in E , that is to say the straight line and respectively the affinety planes.
A affinity subspace can be determined as a subset of its points, or as a point of his and a director subspace. We will start from these geometrical conditions and we will characterize algebrical the straight lines and the planes of the subspace E pertain to a carthesian orthonormed marker R(0; i , j , k ).
Taking in consideration the euclidian structure of a vectorial space director V , will square up to the aspects linked between the angles and distances.
1. Plane in space
In E , space of euclidian geometry , a plane is unique determined by the following conditions:
1) three non-coliniar points
2) a point and two non-parallel straight lines
3) a point and a perpendicular straight line on a plane.
1.1. The plane through three points
Let
be M0, M1, M2![]() E3 three non-coliniar points (affinity
independent). The affinity subspace
E3 three non-coliniar points (affinity
independent). The affinity subspace ![]()
![]() E3 generated by the points M0, M1, M2 has as a director vectorial space a
subspace of dimension two in the vectorial space V , given by:
E3 generated by the points M0, M1, M2 has as a director vectorial space a
subspace of dimension two in the vectorial space V , given by:
V
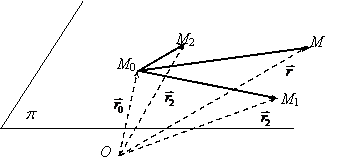
A point M
![]()
![]() if and only if
if and only if ![]()
![]() V
V
fig.1.
If we denote by ![]() =
= ![]() ,
, ![]() =
= ![]() , i = 0, 1, 2 the position
vectors of the points M and respective M0, M1, M2 in the carthesian
mark R (O;
, i = 0, 1, 2 the position
vectors of the points M and respective M0, M1, M2 in the carthesian
mark R (O; ![]() ,
, ![]() ,
, ![]() ), (Oxyz) then the
set of the points from the plane
), (Oxyz) then the
set of the points from the plane ![]() will be characterized
by the vectorial relation :
will be characterized
by the vectorial relation :
![]() , l m I R (1.1)
, l m I R (1.1)
wich it is called the vectorial equation of a plane through three points.
If (x, y, z), (xi, yi, zi) I R3, i = 0, 1, 2 are the coordinates of the points M and respective Mi, i = 0, 1, 2 than the vectorial equation (1.1) written in the carthesian mark (Oxyz) is equivalent to the following equations:
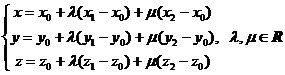 (1.2)
(1.2)
named the parametrical carthesian equations of a plane through three points.
The relation ![]() = l
= l![]() + m
+ m![]() represents the condition of coplanarity of vectors
represents the condition of coplanarity of vectors ![]() ,
, ![]() ,
, ![]() wich is equivalent to
the abolition of the mixed product, that is :
wich is equivalent to
the abolition of the mixed product, that is :
(![]() ,
, ![]() ,
, ![]() ) = 0 or (
) = 0 or (![]() ,
,![]() ,
,![]() ) (1.3)
) (1.3)
In the carthesian coordinates the equation (1.3) is written like this:
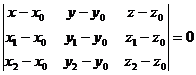 or
or 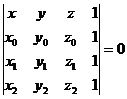 (1.4)
(1.4)
wich is called the carthesian equation of a plane through three points
In particular, the points A (a,
0, 0), B (0, b, 0), C (0, 0, c) situated on the axis of
coordinates Oxyz determins a plane ![]() , and the coordinates of its points satisfy the following equation:
, and the coordinates of its points satisfy the following equation:
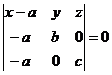 , or
after increment (progress).
, or
after increment (progress).
![]() (1.5)
(1.5)
named the cutting equation of plane p
Remark. The necessary and sufficient
condition for the need of four points Mi(xi,yi, zi),
![]() to be situated in a
plane is:
to be situated in a
plane is:
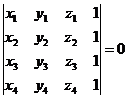 (1.6)
(1.6)
1.2. The plane through one point, parallel with two given directions
Let the point M0 I E3 and the distinct straight lines d1, d2 E . We consider in the point M0 the representative of the vectors ![]() (l1, m1, n1) ,
(l1, m1, n1) , ![]() (l2, m2, n2) parallel to
the straight line d1
respectively d2 (fig.2)
(l2, m2, n2) parallel to
the straight line d1
respectively d2 (fig.2)
The vectors![]() and
and ![]() , linearly independent
generates the vectorial subspace :
, linearly independent
generates the vectorial subspace :
V

fig.2
The point M0
I E3 and the vectorial subspace V determins the bidimentional affinity subspace p E3. One point M
I p if and only if ![]() I V , wich means that the vectors
I V , wich means that the vectors ![]() ,
, ![]() and
and ![]() are coplanar.
are coplanar.
Using the position vectors ![]() and
and ![]() appropriate to points
M and respectively M0, the relation of coplanarity
appropriate to points
M and respectively M0, the relation of coplanarity ![]() is written like this:
is written like this:
![]() (1.7)
(1.7)
named the vecorial equation of the plane through one point, parallel with two directions.
Projecting the equation (1.7) on the axis of coordinates Oxyz in the carthesian system we obtain:
|
|
l m I R |
called the carthesian equation under parametrical form of plane through one point, parallel with two directions.
The coplanar relation of vectors ![]() ,
, ![]() and
and ![]() is characterized by
the abolition of the mixt product of the three vectors, wich means that (
is characterized by
the abolition of the mixt product of the three vectors, wich means that (![]() ,
, ![]() ,
,![]() ) = 0. This way we
obtain the following equation:
) = 0. This way we
obtain the following equation:
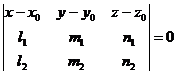 (1.9)
(1.9)
called the carthesian equation of a plane through one point, parallel with two directions.
Remark. In particular, the equation (1.9) can be adapted for other situations known from the elementary geometry, in wich a plane is perfect determined.
Namely: the plane determined by a straight line and a point not-situated on the line, the plane determined by two straight concurent lines and respectively the plane determined by two parallel straight lines.
1.3. The plane through one point , perpendicular on a straight line
The first two cases of a plane determination are specific to an affinity space, the plane taken like the prop set of an affinity subspace of dimension two of the affinity vectorial space E3. By overlaing the properties given by the euclidian structure of the vectorial space V , we can characterize algebricaly the points of a plane through one point and wich should be perpendicular on one given direction.
It is known from the elementary geometry that exists only one plane and
only one wich passes through one point and it is perpendicular on a given
straight line. Algebricaly speaking this fact is conceived like this: if V2
is a vectorial subspace of dimension two in the euclidian vectorial space of
free vectors V3 then it exists an orthogonal unique complement V1,
subspace of dimension one, wich allows writting in direct sum the vectorial
space of free vectors, like this V V2 ![]() V
V
Therefore, the determination of an affinity plane![]() through a point having a vectorial director space on V wich is equivalent to the determining of the plane through one point
having the direction of the normal parallel to the subspace V1
orthogonaly to subspace V
through a point having a vectorial director space on V wich is equivalent to the determining of the plane through one point
having the direction of the normal parallel to the subspace V1
orthogonaly to subspace V
A vector with perpendicular direction on a plane will be named normal vector of the plane or shortly the normaly of the plane.
Let be a point M0 (xo, y0,
z0) I E3 and the not zero vector ![]() (A, B, C)
I V in
the euclidian punctual space E3 having in composition the carthesian
orthonormed mark R (O;
(A, B, C)
I V in
the euclidian punctual space E3 having in composition the carthesian
orthonormed mark R (O; ![]() ,
, ![]() ,
, ![]() ), (fig.3).
), (fig.3).
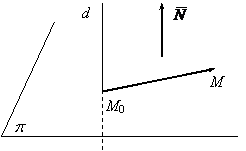
fig.3
A point M(x, y, z) is situated in plane p, the plane in wich M0 is perpendicular on the straight line ![]() , if and only if
, if and only if ![]() is orthogonal on the vector
is orthogonal on the vector ![]() , means that
, means that ![]()
![]() = 0. Using the analitical expression of the scalar product we obtain:
= 0. Using the analitical expression of the scalar product we obtain:
A(x - x0) + B(y - y0) + C(z - z0) (1.10)
is called the equation of a plane through one point and a given normal.
By processing the left part of the equation (1.10) and by denoting with D = - (Ax0 + By0 + Cz0) we obtain:
Ax + By + Cz + D (1.11)
named the general carthesian equation of a plane.
Remarks:
. Any plane p E3 is characterized by a carthesian mark Oxyz by an polynomial equation of first degree in the undetermined x,y,z and reciprocal.
. In the equation (1.11) the coeficients of the undetermined represents the coordinates of the normal vector at a plane. In conseqence, two planes on wich the equations differs by the free term are parallel planes, so, the equation
Ax + By + Cz = l , l I R (1.12)
Represents the
family of parallel planes from space of given normal![]() (A, B, C).
Forl = 0 the equation (1.12) represents the equation of a plane through the
origin.
(A, B, C).
Forl = 0 the equation (1.12) represents the equation of a plane through the
origin.
. The equations of coordinates planes.
Thoes planes are containing the origin, therefore l = 0 and have as normals the vectors of the
mark R (O; ![]() ,
, ![]() ,
, ![]() ),
), ![]() = (1,0,0),
= (1,0,0), ![]() = (0,1,0),
= (0,1,0), ![]() = (0,0,1). We obtain:
= (0,0,1). We obtain:
z the equation of the plane xOy
y the equation of the plane xOz
x the equation of the plane yOz
. The
normal equation of a plane. Lets consider the plane p E3 and point M0 the projection of the origin in the mark R (O; ![]() ,
, ![]() ,
, ![]() ) on the plane p. If we
denote with p the distance from the origin to the plane p, with a b g the angles that makes the vector
) on the plane p. If we
denote with p the distance from the origin to the plane p, with a b g the angles that makes the vector ![]() with the axis of
coordinates then we can write:
with the axis of
coordinates then we can write:
![]() = ||
= ||![]()
![]() = p (cosa
= p (cosa ![]() + cosb
+ cosb![]() + cosg
+ cosg![]()
||![]() || = 1
|| = 1 ![]() cos2a cos2b cos2g
cos2a cos2b cos2g
A point M (x, y, z) situated on the plane p if and only if the vectors ![]() = p cosa
= p cosa ![]() + p
cosb
+ p
cosb![]() + p cosg
+ p cosg![]() si
si ![]() =
= ![]() -
- ![]() = = (x - p
cosa)
= = (x - p
cosa)![]() + (y p cosb)
+ (y p cosb)![]() + (z p cosg)
+ (z p cosg)![]() are orthogonal, wich means
are orthogonal, wich means ![]()
![]() = 0. In
coordinates the condition of orthogonality is equivalent with:
= 0. In
coordinates the condition of orthogonality is equivalent with:
x cosa + y cosb + z cosg - p = 0 (1.13)
named the normal equation of a plane or the equation of a plane under the form of Hess.
In the equation (1.13) p I R represents the distance of the origin to the
plane p and the
quantities cosa, cosb cosg wich has the property cos2a cos2b cos2g =
1 represents the coordinates of the
versor ![]() of the normal
direction of the plane p and
they will be named the director cosinus
of the direction
of the normal
direction of the plane p and
they will be named the director cosinus
of the direction ![]() .
.
If we consider the plane p given by the general
equation Ax + By + Cz +D
= 0, having the normal ![]() = (A, B,
C) and dividing the equation through
= (A, B,
C) and dividing the equation through
![]() we obtain:
we obtain:
![]() (1.14)
(1.14)
named the normalized equation of
the plane p We choose the sign or after if D is negative or positive, forasmuch comparing the equation (1.14) with the equation (1.13) we have ![]()
![]()
![]() , and the free term
, and the free term ![]() , in which p >
0, represents the distance.
, in which p >
0, represents the distance.
1.4. The relative position of two planes
The study of the geometrical positions of two planes p p E3:
planes which intersects after a stright line
parallel planes (strictly)
mixed planes,
it diminishes to the study of the solved system sets formed with the equation given by the two planes.
Let us consider in the orthonormed
carthesian mark R (O; ![]() ,
, ![]() ,
, ![]() ) the planes (p ): A1x + B1y + C1z + D1
= 0 and (p ): A2x + B2y + C2z + D2
= 0.
) the planes (p ): A1x + B1y + C1z + D1
= 0 and (p ): A2x + B2y + C2z + D2
= 0.
If we denote with 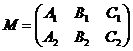 the matrix of the
system
the matrix of the
system
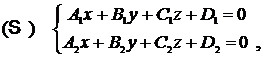 (1.15)
(1.15)
we have the following cases:
- rank M = 2 the system (S ) is simply undetermined compatibile.
The set of solutions of the system ( I ) characterize the geometrical space of the common points of two planes, that is to say the straight line of intersection of the two planes d = p p
- rank M = 1 and Dc = 0 the system (S ) is double undetermined compatible, that is to say the two planes coincide, p s p
- rank M = 1 and Dc 0 system (S ) is incompatible. The two planes dont have any common points, p p
1.5. The relative position of three planes
In the euclidian punctual
space endowed with the carthesian mark R (O; ![]() ,
, ![]() ,
, ![]() ) we consider the
planes:
) we consider the
planes:
p ): A1x + B1y + C1z + D1 = 0
(S ) (p ): A2x + B2y + C2z + D2 = 0
p ): A3x + B3y + C3z + D3 = 0
We denote with:
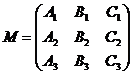 ,
,
the matrix of the system formed with the equations of the three planes.
We have the following cases:
a) rank M = 3 system (S ) is compatible determined. The solution of the system represents the coordinates of the common point of the three planes; we will say that the three planes are concurrent (sheaf of planes).
b) rank M = 2 and Dc system (S ) is simple compatible undetermined. The set of solutions represents the coordinates of the points situated on a common straight line of the three planes. We say that the three planes forms a fascicle of planes.
The rank conditions M = 2 and Dc = 0 are equivalent with the fact that a equation of the system (S ) is a linear combination of the others. If the planes (p ) and (p ) determins a straight line (d) then any plane through the line of intersection is analitically represented as a combination of the equations of the two planes. The equation of the fascicle of the planes through the intersection line of the planes p and p , named the axis of the fascicle, is given by :
l(A x + B1y + C1z + D1) + m(A2x + B2y + C2z + D2) = 0 (1.16)
l m I R, l m
The equation A x + B1y + C1z + D1 + a(A2x + B2y + C2z + D2) = 0, a I R
represents the equation of the fascicle through the straight line (d) from which is missing the plane p
In particular, the axis Ox thought as the intersection of the planes xOy and xOz, determins the fascicle of the planes through Oz characterized by:
ly mz (1.17)
c) rank M = 2 and Dc system (S ) is incompatible. If two planes are intersected after a straight line, the third plane being parallel with the intersection line of the first two planes (the planes are forming a prism).
d) rank M = 1 and ![]() =
= ![]() = 0 the system (S ) is compatible double undetermined. The three
planes are mixed.
= 0 the system (S ) is compatible double undetermined. The three
planes are mixed.
e) rank M = 1 and ![]() the system (S
) is incompatible.
The planes are parallel (strict or two can be mixed).
the system (S
) is incompatible.
The planes are parallel (strict or two can be mixed).
2. The straight line in space
Let be R (O; ![]() ,
, ![]() ,
, ![]() ), an orthonormed carthesian mark in the punctual euclidian
space E = (E3,
V j). Either point M I E we can associate the position vector
), an orthonormed carthesian mark in the punctual euclidian
space E = (E3,
V j). Either point M I E we can associate the position vector ![]() , where the ternary (x, y, z) I R , the
coordinates of the vector
, where the ternary (x, y, z) I R , the
coordinates of the vector ![]() in base will be named the coordinates of point
M.
in base will be named the coordinates of point
M.
In the geometrical space E3, a straight line is unique determined by the following conditions:
- a point and a given direction
- two distinct points
- the intersection of two planes
2.1. The straight line determined by a point and a direction
Let be a point M0 I E and the non-zero vector ![]() I V . The
non-zero vector
I V . The
non-zero vector ![]() generates the onedimenssion vectorial
subspace V
generates the onedimenssion vectorial
subspace V

In these conditions the affinity subspace
which contains the point M and which allows on V 1 as a director space, will have as support set
the straight line(d) whom the points
are given by: ![]()
The condition ![]() I V takes place iff l I R such that
I V takes place iff l I R such that ![]() = l
= l![]() . Writting
. Writting ![]() =
= ![]() we obtain
we obtain
![]() lIR (2.1)
lIR (2.1)
named the vectorial equation of a straight line (d) through point M0 having the direction given by the vector ![]() .
.
If we project the relation
(2.1) on the axis of the carthesian mark
R(O,![]() ,
,![]() ,
,![]() ) we obtain :
) we obtain :
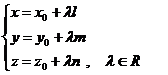 (2.2)
(2.2)
named the parametrical equations of the straight line d through point M0(x0, y0,
z0) having the direction
given by the vector ![]() .
.
The
vector ![]() = (l, m, n)
I V will be named vectorial director of the straight line (d) and the coordinates l, m,
n I R will be named director parameters of the
straight line (d).
= (l, m, n)
I V will be named vectorial director of the straight line (d) and the coordinates l, m,
n I R will be named director parameters of the
straight line (d).
If the director
vector is the versor ![]() , which forms the
angles a b g with the axis of the
coordinates Ox, Oy, Oz, then the director parameters :
, which forms the
angles a b g with the axis of the
coordinates Ox, Oy, Oz, then the director parameters :
cosa, cosb, cosg, the coordinates of the versor ![]() , will be named the
director cosinus of the straight line (d).
, will be named the
director cosinus of the straight line (d).
The director cosinus of a direction in space satisfies the relation
cos2a cos2b cos2g =
Remark: the equations (2.1) or the equivalent form (2.2) guvernates the exact uniform straight line of a material point.
Eliminating the parameter l from the equations (2.2) we obtain the folowing equations:
![]() (2.3)
(2.3)
named the
canonical carthesian equations (
known as proportions) of the
stright line d through point M0(x0,
y0, z0) and with the
direction given by the vector ![]() = (l, m,
n).
= (l, m,
n).
Remark: the canonical equations are being written when one or two director parameters are zero, which corresponds in this case that the corresponding denominator is zero and the equations are efectivly given by the equalizing of the equivalent product of the proportions formed.
Let be M1, M2 I E two distinct points. The affinity subspace generated by these points will have as a vectorial director the onedimension subspace V V given by
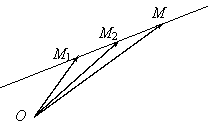
V
fig. 2
In other words a point M I E belongs to a support set of the affinity subspace generated by the
points M1 and M2, that is M
situated on the
straight line through the two points, if and only if the vectors ![]() and
and ![]() are collinear. Thus, the set of points of the
straight line M1 and M2 will be characterized by the vectorial
relation:
are collinear. Thus, the set of points of the
straight line M1 and M2 will be characterized by the vectorial
relation:
![]() l I R
l I R
or
![]() (2.4)
(2.4)
named the vectorial equation of a straight line through two points.
In the carthesian mark R (O; ![]() ,
, ![]() ,
, ![]() ),
considering M(x, y, z) , M1(x1, y1,
z1) and M2(x2, y2,
z2), we will obtain:
),
considering M(x, y, z) , M1(x1, y1,
z1) and M2(x2, y2,
z2), we will obtain:
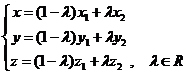 (2.5)
(2.5)
named the parametrical equations of the straight line through two points .
Remark: For l I (0, 1) the equations (2.5) provides us the sets of points on the
straight line (d) within the points M1 and M2,
and for l I R
[0, 1] we obtain the points of the
straight line (d), the exterior of the segment M1M2. For ![]() we obtain the
coordinates of the middle of the segment M1M2.
we obtain the
coordinates of the middle of the segment M1M2.
The elimination of the parameter l I R in the equation (2.5) or imposing the proportionality of the coordinates of two collinear vectors , we obtain
![]() (2.6)
(2.6)
which is called the carthesian equation in a canonical shape of a straight line through two points.
2.3. The straight line as an intersection of two planes
It is known from the elementry geometry that two nonparallel planes are intersecting after a straight line (d). In the former paragraph this geometrical situation is characterized analiticaly by a system of undetermined compatible linear equations, formed with the equations of two planes. Thus, the equations of the system
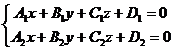 (2.7)
(2.7)
will be named the equations of the straight line (d) given by the intersection of two planes.
A solution (x0,
y0, z0) of the system
(2.7) will characterize a point of the straight line (d)
and the vector ![]() , where
, where ![]() and
and ![]() are the norms (normalele) of the two planes
which determins the straight line (d).
are the norms (normalele) of the two planes
which determins the straight line (d).
Remark :
The carthesian equations (2.3) and (2.6) of a straight line in space can be translated as a system of two linear equations, that is the straight line (d) considered as an intersection between two planes.
2.4. The relative positions of two straight lines
Let be the straight lines (d1) and (d2) given by the equations
(d1)
![]()
(d2)
![]()
We consider the vectors ![]() =
(l1, m1, n1),
=
(l1, m1, n1),
![]() = (l2, m2, n2)
director vectors of the straight lines (d1)
respective (d2) and the vectors
= (l2, m2, n2)
director vectors of the straight lines (d1)
respective (d2) and the vectors ![]() , where M1(x1, y1, z1)
I d1 respective M2(x2, y2,
z2) I d2.
, where M1(x1, y1, z1)
I d1 respective M2(x2, y2,
z2) I d2.
We have the cases:
a) if (![]() ,
, ![]() ,
, ![]() ) 0 the straight lines (d1)
and (d2) are noncoplanar or are some certain straight
lines in space (deformed seted in space).
) 0 the straight lines (d1)
and (d2) are noncoplanar or are some certain straight
lines in space (deformed seted in space).

In this case exists a common direction unique
normal on the two straight lines, given by ![]() =
=![]()
![]() and so a unique straight line which is underpins on the two
straight lines having the direction
and so a unique straight line which is underpins on the two
straight lines having the direction ![]() (fig. 3), named common perpendicular of the straight lines (d1) and (d2).
(fig. 3), named common perpendicular of the straight lines (d1) and (d2).
fig. 3
The common perpendicular (d) is given by the intersection of the planes p and
p p the plane through the straight line (d1) parallel to ![]() and p - the plane through (d2) parallel to
and p - the plane through (d2) parallel to ![]() . The equations of the
common perpendicular are :
. The equations of the
common perpendicular are :
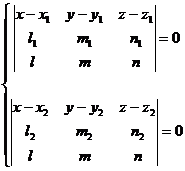 (2.8)
(2.8)
where (l, m,
n) = ![]() =
= ![]()
![]()
b) if (![]() ,
, ![]() ,
, ![]() ) = 0 the straight lines (d1) and (d2) are coplanar
) = 0 the straight lines (d1) and (d2) are coplanar
b1) ![]() l
l![]() - concurrent straight
lines
- concurrent straight
lines
b2) ![]() = l
= l![]() - parallel straight
lines (strictly)
- parallel straight
lines (strictly)
b3) ![]() = l
= l![]() and
and ![]() = m
= m![]() - submerged straight
lines
- submerged straight
lines
3. Angles and distances
Let be (d) a straight line in euclidian punctual space E3. On the line (d) can be established two ways of the route. A straight line (d) along with a way of the route it is called oriented straight line.
If ![]() is the director
vector of the straight line (d), then we will choose the way of the
route on the line the way of
is the director
vector of the straight line (d), then we will choose the way of the
route on the line the way of ![]() (positive way).
(positive way).
Let be the plane p E3 having the normal vector ![]() . The plane has two faces and choosing a way on the normal is
equivalent with choosing a face of the plane. A plane p along with a choice of the way on the
normal is called oriented plane. Will
choose the way on the normal and the orientation is given by
. The plane has two faces and choosing a way on the normal is
equivalent with choosing a face of the plane. A plane p along with a choice of the way on the
normal is called oriented plane. Will
choose the way on the normal and the orientation is given by ![]()
3.1. The angle of two straight line in space
Let be the straight lines (d1) and (d2) oriented by the director vectors ![]() = (l1, m1, n1)
and respectively
= (l1, m1, n1)
and respectively ![]() = (l2, m2, n2).
= (l2, m2, n2).
Through the angles of the straight lines (d1) and (d2)
we will understand the angle j I p], angle between the vectors ![]() and
and ![]() , given by
, given by
cosj = 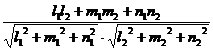 (3.1)
(3.1)
In particular we have:
d1 ![]() d
d ![]()
![]() = 0 l1l2+m1m2+n1n2
= 0
= 0 l1l2+m1m2+n1n2
= 0
![]()
![]()
![]() =
= ![]()
![]()
3.2. Angle of two planes
Let be the unparallel planes p and p , given by
p A1x + B1y + C1z + D1 = 0
p ) A2x + B2y + C2z + D2 = 0
In elementary geometry the angle of two unparallel planes is defined as
the diedral angle of the two planes. This angle is equal or suplementar with
the angle of the vectors ![]() and
and ![]() ,
normal vectors of the planes p respectively p
,
normal vectors of the planes p respectively p
We accept that the diedral angle determined by the oriented planes p and p2 to
be mesured through the angle between ![]() 1 and
1 and ![]() 2 . This angle is given by
2 . This angle is given by
cosj =  (3.2)
(3.2)
In particularly p ![]() p A1A2+B1B2+C1C2 = 0
p A1A2+B1B2+C1C2 = 0
3.3. The angle between a straight line and a plane
The angle between a line and a plane is defined in elementary geometry as the angle between a line and its orthogonal projection on the plane.
Let be the the line (d)
oriented by the director vector ![]() = (l, m,
n) and the plane p oriented by the normal
= (l, m,
n) and the plane p oriented by the normal ![]() (fig. 5)
(fig. 5)

fig. 5
The angle j I ![]() ] between the line (d)
and plane p is tied to the angle q, the angle of the vectors
] between the line (d)
and plane p is tied to the angle q, the angle of the vectors ![]() and
and ![]() , through the relations q
, through the relations q ![]() j we obtain
j we obtain ![]() .This way we find :
.This way we find :
![]() =
= ![]() (3.3)
(3.3)
In particularily:
d p ![]()
![]() = 0 lA + mB + nC = 0,
= 0 lA + mB + nC = 0,
d ![]() p
p ![]()
![]() =
= ![]()
![]() .
.
3.4 The distance from a point to a straight line
We remind that the distance between two subsets S1 and S2 in a metric space is given by d ( S1, S2) = inf .

In
the euclidian punctual space E endowed with euclidian metric the distance between two subsets is reduced
to a distance between two points. Thus, the distance from a point to a straight
line is given by the distance between a point and its orthogonal projection on
the straight line (fig.
6)
fig. 6
Let be the line (d) through point M0, oriented through the director vector ![]() , point A exterior of the line and A its projection on the straight line (d). By determining the plane A , as the intersection of the line (d) with the plane through A orthogonal to the line, we obtain d (A, d) = d (A, A Thus, by constructing the parallelogram determined by the vectors
, point A exterior of the line and A its projection on the straight line (d). By determining the plane A , as the intersection of the line (d) with the plane through A orthogonal to the line, we obtain d (A, d) = d (A, A Thus, by constructing the parallelogram determined by the vectors ![]() and
and ![]() , we
obtain
, we
obtain
d (A,
d) = d (A, A ![]() (3.4)
(3.4)
3.5. The distance from a point to a plane
The distance from a point M0 to a plane (p Ax + By + Cz + D = 0 is given by the distance between the point M0(x0, y0, z0) and the point M (x , y , z ), its orthogonal projection on the plane p
We determine the coordinates (x , y , z ) of the point M , by solving the system formed by the equations of the planes and the equations of the straight lines through the point M0 orthogonal on the plane, that is to be:
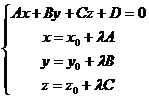 (3.5)
(3.5)
The parameter on the line is suiting M , denoted with l , is given by
l = - ![]() and we obtain
and we obtain
d (M0,M ![]()
= ![]() =
= ![]()
and the distance from the point M0 to plane p is given by
d (M0,
p ![]() (3.6)
(3.6)
Remark: The distance from a point M0 to a plane p is obtained by taking the modulus of the expression obtained through the replacing of the given point coordinate in the left member of the normalized equation of the plane.
3.6. The distance between two certain straight lines in space
Let be the certain lines in space
(d1)
![]()
(d2)
![]()
Let be (d) the common perpendicular of the lines (d1) and (d2) and P1 respectively P2 its contact points (d1) respectively (d2).
We construct the determined parallelipiped by the vectors ![]() = (x2-x1, y2-y1, z2-z1),
= (x2-x1, y2-y1, z2-z1),
![]() =(l1, m1, n1) and
=(l1, m1, n1) and![]() = (l2, m2, n2). (fig. 7)
= (l2, m2, n2). (fig. 7)
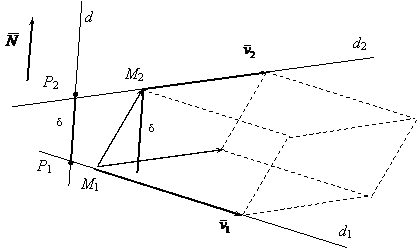
fig. 7
The distance between the straight lines (d1) and (d2) is given by the distance between the contact points of the common perpendicular to the two lines, the distance which represents the height of the builded parallelipiped.
Thus, we obtain:
d (d1, d2) = d (P1, P2) = ![]() (3.7)
(3.7)
4. Problems
1. It is given A ( 3, 1, 0), B ( 2, 1, -1), C ( 3, 2, 1). Write the equation of a plane :
a) which passes through A, B, C;
b) which passes through B and is parallel xOy;
c) which passes through C and containes the axis Oz;
d) which passes through B, C and is parallel to Oy.
. Write the equation of the plane which passes through point M ( 2, 0, 1) and is perpendicular on the planes (P1) : x + y + z = 0 and (P2): x - 2y + 3z = 1.
. Write the equation of a plane parallel to the plane (P) x + y + +z = 3 and which passes through the middle of the segment determined by the points M1 ( 1, 3, 2) and M ( -1, 3 , 4).
. Determine the equation of the plane which passes through M ( -1, 1, 0) and cuts on the axis of coordinates proportional segments with numbers 2, 3, 4.
.
Let be the plane 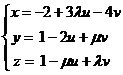 .
.
Find l and m thus such that the plane to be
orthogonal on the vector ![]() ( 1, 7, 11). Write the
general equation of the plane.
( 1, 7, 11). Write the
general equation of the plane.
. Let be the triangle A, B, C with A ( 0, 2, 0), B ( 3, 2, 1),
C ( 0, 1, 2). Write the equations:
a) the height from A;
b) the median from B;
c) the mediator of the flank AB.
. Write the equation of the straight line which passes through M (1,-1,1) and is parallel to the line of intersection of the planes (P1) x + y = 3 and (P2) x - z = 1.
. A mobile M is moving in space on the trajectory given by
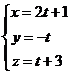
Determine the moment t at which the mobile is contained in plane x + y + z = 0 and write the carthesian equation of this trajectory.
.
Find a b I R such that the straight line ![]() is contained in plane x z = 0 and to pass through M ( 1, 1, 1).
is contained in plane x z = 0 and to pass through M ( 1, 1, 1).
. Write the equation of the plane which passes through M0 ( 2, -1, 1) and is perpendicular on the straight line defined by the planes (P1) : x + 2y + 2z + 2 = 0 si (P2) : x - y + z + 1= 1.
.
Write the equation of the plane which passes through the middle of the segment M ( 1, -1, 2), N ( 4, -3, 1), is parallel to the line ![]() and perpendicular to
the plane x 2y z 1 = 0.
and perpendicular to
the plane x 2y z 1 = 0.
. Write the equations of the lines contained in plane (P) x + 3y+ 2z -2 = 0, which is sustained on the straight line x = y = z and is parallel to the plane 4x y z 3 = 0.
. Write
the projection equations of the straight line ![]() on the plane 3x
2y + z 4 = 0.
on the plane 3x
2y + z 4 = 0.
. Write the equation of a parallel plane (P) 3x + 5y + z = 0 which passes through point M ( 2, 0 , 5).
.
Write the plane which passes through A
( 3, 1, -2) and containes the straight line ![]() .
.
. Let be the point M ( 2, 1, 0) and the plane (P) 2x + 2y + z = 1. Determine:
a) the projection of M on the plane;
b) the simetric of M towards the plane;
c) the distance from M to (P).
.
Let be the straight line (d) ![]() and the plane (P) 2x - y + z = 0. Determine the
projection of the straight line (d)
on the plane (P).
and the plane (P) 2x - y + z = 0. Determine the
projection of the straight line (d)
on the plane (P).
. Write the equation of a plane which passes
through the line ![]() and which is
perpendicular on the plane x + y + z = 0.
and which is
perpendicular on the plane x + y + z = 0.
. Write the equation of a straight line which passes through A ( 3, 1, -1) and sustaines on the straight lines
a)
![]() and
and ![]()
b)
![]() and x = -t, y = 2t + 1, z = 3t.
and x = -t, y = 2t + 1, z = 3t.
. On the
straight line ![]() find a point equal secluded from the points A (3, 14, 4) and B (5, -13, -2).
find a point equal secluded from the points A (3, 14, 4) and B (5, -13, -2).
. Find the angles between the straight lines
![]() and
and ![]()
. Calculate the angle which makes with the
straight line (d) : ![]() and the plane 2x
+ 2y z 3 = 0.
and the plane 2x
+ 2y z 3 = 0.
. Determine the angle between the planes x + y + 2z = 1, 2x y + 2z = 3.
. Write the equation of the common perpendicular and calculate the distance between the straight lines
a)
(d1): ![]() and (d2):
and (d2): ![]()
b)
(d1): ![]() and (d2):
and (d2): ![]()
. Show that the straight lines (d1):
![]() and (d2):
and (d2): ![]() are certain in space and determine the
distance between them.
are certain in space and determine the
distance between them.
. Determine a and b such that the planes:
p ): x + 2y + z = a
p ax
p ): x + by + z = 0,
a) intersect after a straight line;
b) intersect in a point;
c) form a prism.
. Determine
the simetric of the straight line (D):
![]() toward the plane xOy.
toward the plane xOy.
. Determine the simetrical of the plane 2x + y 2z = 1 toward the plane x + y + z = 0.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1854
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved