| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
This section presents Strassen's remarkable recursive
algorithm for multiplying n ![]() n matrices
that runs in
n matrices
that runs in ![]() (nlg
7) = O(n2.81) time. For sufficiently large n,
therefore, it outperforms the naive
(nlg
7) = O(n2.81) time. For sufficiently large n,
therefore, it outperforms the naive ![]() (n3)
matrix-multiplication algorithm MATRIX MULTIPLY from Section 26.1.
(n3)
matrix-multiplication algorithm MATRIX MULTIPLY from Section 26.1.
Strassen s algorithm can be viewed as an application of a familiar design
technique: divide and conquer. Suppose we wish to compute the product C
= AB, where each of A, B, and C are n ![]() n
matrices. Assuming that n is an exact power of 2, we divide each of A,
B, and C into four n/2
n
matrices. Assuming that n is an exact power of 2, we divide each of A,
B, and C into four n/2 ![]() n/2 matrices,
rewriting the equation C = AB as follows:
n/2 matrices,
rewriting the equation C = AB as follows:

(Exercise 2-2 deals with the situation in which n is not an exact power of 2.) For convenience, the submatrices of A are labeled alphabetically from left to right, whereas those of B are labeled from top to bottom, in agreement with the way matrix multiplication is performed. Equation (9) corresponds to the four equations
r = ae + bf ,Each of these four
equations specifies two multiplications of n/2 ![]() n/2 matrices
and the addition of their n/2
n/2 matrices
and the addition of their n/2 ![]() n/2
products. Using these equations to define a straightforward divide-and-conquer
strategy, we derive the following recurrence for the time T(n) to
multiply two n
n/2
products. Using these equations to define a straightforward divide-and-conquer
strategy, we derive the following recurrence for the time T(n) to
multiply two n ![]() n
matrices:
n
matrices:
Unfortunately, recurrence
(14) has the solution T(n) = ![]() (n3),
and thus this method is no faster than the ordinary one.
(n3),
and thus this method is no faster than the ordinary one.
Strassen discovered a
different recursive approach that requires only 7 recursive multiplications of n/2
![]() n/2 matrices
and
n/2 matrices
and ![]() (n2)
scalar additions and subtractions, yielding the recurrence
(n2)
scalar additions and subtractions, yielding the recurrence
Strassen's method has four steps:
1. Divide the input
matrices A and B into n/2 ![]() n/2
submatrices, as in equation (9).
n/2
submatrices, as in equation (9).
2. Using ![]() (n2)
scalar additions and subtractions, compute 14 n/2
(n2)
scalar additions and subtractions, compute 14 n/2 ![]() n/2 matrices
A1, B1, A2, B2,
. . . , A7, B7.
n/2 matrices
A1, B1, A2, B2,
. . . , A7, B7.
3. Recursively compute the seven matrix products Pi = AiBi for i = 1, 2, . . . , 7.
4. Compute the desired
submatrices r, s, t, u of the result matrix C by adding and/or
subtracting various combinations of the Pi matrices,
using only ![]() (n2)
scalar additions and subtractions.
(n2)
scalar additions and subtractions.
Such a procedure satisfies the recurrence (15). All that we have to do now is fill in the missing details.
It is not clear exactly how Strassen discovered the submatrix products that are the key to making his algorithm work. Here, we reconstruct one plausible discovery method.
Let us guess that each matrix product Pi can be written in the form
Pi AiBiwhere the coefficients ![]() ij,
ij,
![]() ij
are all drawn from the set . That is, we guess that each
product is computed by adding or subtracting some of the submatrices of A,
adding or subtracting some of the submatrices of B, and then multiplying
the two results together. While more general strategies are possible, this
simple one turns out to work.
ij
are all drawn from the set . That is, we guess that each
product is computed by adding or subtracting some of the submatrices of A,
adding or subtracting some of the submatrices of B, and then multiplying
the two results together. While more general strategies are possible, this
simple one turns out to work.
If we form all of our products in this manner, then we can use this method recursively without assuming commutativity of multiplication, since each product has all of the A submatrices on the left and all of the B submatrices on the right. This property is essential for the recursive application of this method, since matrix multiplication is not commutative.
For convenience, we shall
use 4 ![]() 4 matrices to
represent linear combinations of products of submatrices, where each product
combines one submatrix of A with one submatrix of B as in equation
(16). For example, we can rewrite equation (10) as
4 matrices to
represent linear combinations of products of submatrices, where each product
combines one submatrix of A with one submatrix of B as in equation
(16). For example, we can rewrite equation (10) as
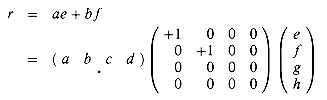
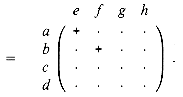
The last expression uses
an abbreviated notation in which '+' represents +1, '![]() represents 0,
and -' represents -1. (From here on, we omit the row and column
labels.) Using this notation, we have the following equations for the other
submatrices of the result matrix C:
represents 0,
and -' represents -1. (From here on, we omit the row and column
labels.) Using this notation, we have the following equations for the other
submatrices of the result matrix C:
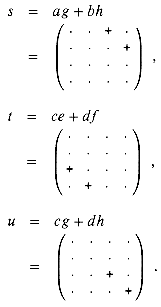
We begin our search for a faster matrix-multiplication algorithm by observing that the submatrix s can be computed as s = P1 + P2, where P1 and P2 are computed using one matrix multiplication each:
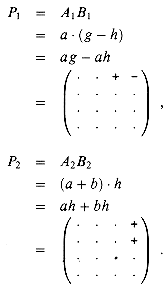
The matrix t can be computed in a similar manner as t = P3 + P4, where
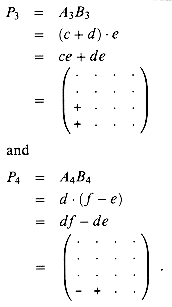
Let us define an essential term to be one of the eight terms appearing on the right-hand side of one of the equations (10)--(13). We have now used 4 products to compute the two submatrices s and t whose essential terms are ag, bh, ce, and df . Note that P1 computes the essential term ag, P2 computes the essential term bh, P3 computes the essential term ce, and P4 computes the essential term df. Thus, it remains for us to compute the remaining two submatrices r and u, whose essential terms are the diagonal terms ae, bf, cg, and dh, without using more than 3 additional products. We now try the innovation P5 in order to compute two essential terms at once:
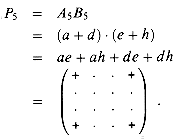
In addition to computing both of the essential terms ae and dh, P5 computes the inessential terms ah and de, which need to be cancelled somehow. We can use P4 and P2 to cancel them, but two other inessential terms then appear:
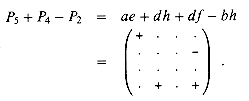
By adding an additional product
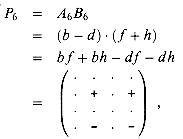
however, we obtain
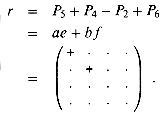
We can obtain u in a similar manner from P5 by using P1 and P3 to move the inessential terms of P5 in a different direction:
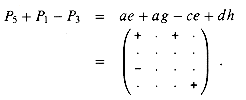
By subtracting an additional product
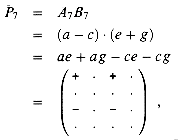
we now obtain
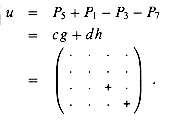
The 7 submatrix products P1, P2, . . . , P7 can thus be used to compute the product C = AB, which completes the description of Strassen's method.
The large constant hidden in the running time of Strassen s algorithm makes it impractical unless the matrices are large (n at least 45 or so) and dense (few zero entries). For small matrices, the straightforward algorithm is preferable, and for large, sparse matrices, there are special sparsematrix algorithms that beat Strassen's in practice. Thus, Strassen s method is largely of theoretical interest.
By using advanced
techniques beyond the scope of this text, one can in fact multiply n ![]() n
matrices in better than
n
matrices in better than ![]() (n1g
7) time. The current best upper bound is approximately O(n2.376).
The best lower bound known is just the obvious
(n1g
7) time. The current best upper bound is approximately O(n2.376).
The best lower bound known is just the obvious ![]() (n2)
bound (obvious because we have to fill in n2 elements of the
product matrix). Thus, we currently do not know how hard matrix multiplication
really is.
(n2)
bound (obvious because we have to fill in n2 elements of the
product matrix). Thus, we currently do not know how hard matrix multiplication
really is.
Strassen s algorithm does not require that the matrix entries be real numbers. All that matters is that the number system form an algebraic ring. If the matrix entries do not form a ring, however, sometimes other techniques can be brought to bear to allow his method to apply. These issues are discussed more fully in the next section.
Use Strassen s algorithm to compute the matrix product
![]()
Show your work.
How would you modify
Strassen s
algorithm to multiply n ![]() n
matrices in which n is not an exact power of 2? Show that the resulting
algorithm runs in time
n
matrices in which n is not an exact power of 2? Show that the resulting
algorithm runs in time ![]() (n1g
7).
(n1g
7).
What is the largest k
such that if you can multiply 3 ![]() 3 matrices
using k multiplications (not assuming commutativity of multiplication),
then you can multiply n
3 matrices
using k multiplications (not assuming commutativity of multiplication),
then you can multiply n ![]() n
matrices in time o(n1g 7)? What would the running time
of this algorithm be?
n
matrices in time o(n1g 7)? What would the running time
of this algorithm be?
V. Pan has discovered a way of multiplying 68 ![]() 68 matrices
using 132,464 multiplications, a way of multiplying 70
68 matrices
using 132,464 multiplications, a way of multiplying 70 ![]() 70 matrices
using 143,640 multiplications, and a way of multiplying 72
70 matrices
using 143,640 multiplications, and a way of multiplying 72 ![]() 72 matrices
using 155,424 multiplications. Which method yields the best asymptotic running
time when used in a divide-and-conquer matrix-multiplication algorithm? Compare
it with the running time for Strassen s algorithm.
72 matrices
using 155,424 multiplications. Which method yields the best asymptotic running
time when used in a divide-and-conquer matrix-multiplication algorithm? Compare
it with the running time for Strassen s algorithm.
How quickly can you
multiply a kn ![]() n matrix
by an n
n matrix
by an n ![]() kn matrix,
using Strassen s
algorithm as a subroutine? Answer the same question with the order of the input
matrices reversed.
kn matrix,
using Strassen s
algorithm as a subroutine? Answer the same question with the order of the input
matrices reversed.
Show how to multiply the complex numbers a + bi and c + di using only three real multiplications. The algorithm should take a, b, c, and d as input and produce the real component ac - bd and the imaginary component ad + bc separately.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1312
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved