ECONOMETRICS ASSIGNMENT - REGRESSION MODEL

Academy of Economic Studies

International Business and Economics

ECONOMETRICS ASSIGNMENT

REGRESSION MODEL

Executive Summary

In this chapter I would like to justify why of all indicators and from all data bases existing I specifically chose verifying the intensity of the relationship between a countrys total advertising expenditures and its GDP.

For once, it will help me with my Dissertation paper which is on advertising, domain Ive recently came in touch with by working at a production company.

Second, the overall increase in the importance given to this sector, with the gigantic amounts spent in producing a TV commercial are raising a good question mark regarding how much does a countrys GDP and welfare influences these spending.

I chose UK because they put a lot of emphasis on their advertising campaigns, having some of the biggest and well-known leading worldwide

commercial production companies, among which I can mention: Radical Media (with who I got the opportunity to work), HIS, Factory Films, Tangerine Films, Independent Media, Mind Works Media UK and also hosting some of the largest global marketers that have a strong word when it comes to their contribution to the Worlds GDP.

All the calculations made to prove the validity of the model were made in Excel and are further attached as ANEXES in the end of the Assignment.

2. Introduction

Advertising is a small part of the day-to-day life of business, governments and of the publics with which each seeks to engage. It is, on the other hand, a business that offers the people who work in and with it endless excitement, fascination, frustration and, sometimes, satisfaction together with the opportunity, from time to time, for a great deal of fun and even for making a massive contribution to the success of a brand.

There is an underlying reason why ad expenditures as a whole has not returned to its 1989 peak share of GDP in the UK. Advertising is not the whole of the communications mix, and the most advertising statistics do not include direct marketing, let alone PR, sales promotion, design and corporate identity, sponsorship and some mirror media nor do they yet include the Internet, which is undoubtedly the fastest growing form of marketing communication, though still from a very small base everywhere outside the USA. All the available evidence shows that direct mail has been growing faster than media advertising in recent years, and PR expenditures have certainly grown very fast in the last three years. Data on sales promotion expenditure are extremely hard to come by, but US evidence, and broader estimates by WPP Group, suggest that advertising accounts for only 42% of total marketing communications expenditures world-wide (including market research), and less than 35% in the UK. As long as 1986, WPP annual report highlighted the rapid growth of sales promotion expenditures, and this remains a world-wide phenomenon.

3. Data Description

As we know, Gross Domestic Product (GDP) is an integral part of the UK national accounts and provides a measure of the total economic activity in a region. GDP is often referred to as one of the main 'summary indicators' of economic activity and references to 'growth in the economy' are quoting the growth in GDP during the latest quarter.
In the UK three different theoretical approaches are used in the estimation of one GDP estimate.

GDP from the output or production approach - GDP(O) measures the sum of the value added created through the production of goods and services within the economy (our production or output as an economy). This approach provides the first estimate of GDP and can be used to show how much different industries (for example, agriculture) contribute within the economy.

GDP from the income approach - GDP(I) measures the total income generated by the production of goods and services within the economy. The figures provided breakdown this income into, for example, income earned by companies (corporations), employees and the self employed.

GDP from the expenditure approach - GDP(E) measures the total expenditures on all finished goods and services produced within the economy.
The estimates are 'Gross' because the value of the capital assets actually worn away (the 'capital consumption') during the productive process has not been subtracted.

Thus, by analyzing the values of GDP by expenditure it will prevail how much its variation explains the variation in the total advertising figures.

Advertising is an activity with significance for many countries economies: total ad spending runs around +/ - 1% of GDP in most developed countries.

In the UK, while ad agencies as such, employ only some 15 000 people, it has been estimated that advertising as a whole is responsible for nearly 100 000 jobs, or 0.4% of total employment. This includes people working in business supplying the ad industry studios, TV production houses, printers, etc. and advertising staff in client organizations and the media.

Advertising expenditures, as shown in the statistics published by the Advertising Association, consist of two elements: display advertising and classified advertising, of which display is the dominant sector, though classified is very important for some media. Advertising is sensitive to the state of the economy as a whole it is not merely vulnerable to both downturns and upswings, but it moves rather rapidly in response to either. Classified advertising, in fact, is a valuable lead indicator of economic progress, because virtually half of it, at least in the UK, consists of recruitment advertising, which reflects companies experience and expectations of their markets precisely.

Advertising thus shows considerable mood swings in line with the growth or stagnation of the economy. Through much of the 1970s, the industry in the UK was in decline: the 1980s saw a sustained boom after the 1981-82 recession, followed by hard times in the early 1990s, and by 1998, display advertising had still not recovered to its 1989 percentage share of GDP.

4. Analysis

4. a) Collecting the data

In order to determine at what extent does the wealth of a country determines the total expenditures in the advertising sector, we will analyze a model taking as independent variable (x),UKs GDP for a 20 year period starting with 1985 and proving how it influences the dependent variable (y), represented by the advertising expenditures in current prices.

The data was collected from several sources so that the GDP values initially expressed in million dollars were converted at a parity of 0.509 pound/dollar as shown in the following table:

Parity: / $ =0.509

Figure 1. UK advertising expenditure and GDP 1985-2004

Source: www.unctad.org and A.A., Advertising Statistics Yearbook 1998, NTC Publications), https://www.ipa.co.uk/resource_centre/totaladspend.cfm

4.b) Graphical representation Scatter diagram

Specifying the econometrical model implies choosing a function f(x) which can describe the relationship between the 2 variables.

The graphical representation of the data presented in Table 1 is made through a scatter diagram which shows that there is a positive relationship between UKs GDP by expenditure and the advertising expenditures from 1985 till 2004, since the two variables tend to move in the same direction forming a linear pattern as follows:

Figure 2. The relation between UKs GDP and Total advertising expenditures in 1985-2004

Source: Figure 1. UK advertising expenditure and GDP 1985-2004

Both the equation and the value of R² displayed on the diagram, we shall see, that are the same as the ones obtained after making all the computations and their values will be described when analyzing the regression model.

4.c) The Regression

After collecting the data and drawing the graph, the next step is to create the regression model using the Regression function in Excel, which automatically generated the Summary output:

Figure 3. Summary output

Where:

• Multiple R (r) = Coefficient of correlation. Is used to characterize the intensity of the relation between variables, independent of the type of the connection or the number of variables taken into consideration.

It is calculated as a ratio between covariance and the product of the

standard deviation of the two variables, as in the formula:

r =

The value of 0.94 obtained in the table shows that there is a strong positive association between UKs GDP by expenditure and the advertising expenditures, since it falls in the interval (0.95 , 0.75] and every point falls on a increasing regression line.

• R square = Coefficient of determination. Shows that the linear regression function catches 90% from the total variation of the advertising expenditures (yi) and it is calculated according to the formula:

R² =

• Standard Error (S) = S_nYn = =

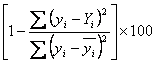
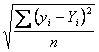
The value obtained in the summary output reveals that there is only a slight difference of ~ 1,39 between the real values and the theoretical ones.

• Adjusted R-Square = 1 [ MS error / (SS total / df total)

Accounts for the number of predictors in your model and is useful for comparing models with different numbers of predictors.

Next, its easy to determine the equation of regression Y=a+bx+

based on the coefficients obtained in the ANOVA table.

Figure 4. ANOVA

So the equation will be :

Y= 1.2506 + 0.000004*x

Where: a = 1.2506 ( intercept) ; it indicates the value of Y when the x=0;

b = 0.0000004 (the slope of the line)

The interpretation of the equation is that an increase of 1 pound in UKs GDP by expenditures in one year (xi), will determine an increase of 0.000004 pounds in the total advertising expenditures of UK in that year.

The formulas for the other coefficients that appeared whilst creating the regression model are encountered below along with the afferent explanations.

• Sum of squares (SS) - The sum of squared distances. SS Total is the total variation in the data. SS Regression is the portion of the variation explained by the model, while SS Error is the portion not explained by the model and is attributed to error.

• Degrees of freedom (d.f.). Indicates the number of independent pieces of information involving the response data needed to calculate the sum of squares. The degrees of freedom for each component of the model are:

DF Regression = p

DF Error = n - p - 1

Total = n - 1

where n = number of observations and p = number of predictors.

• MS Regression (Mean square regression) = the ratio of SS Regression and DF Regression.

• MS Error (Mean square error) = is the variance around the fitted regression line. MS Error = s. The formula is:

MS Error = SS Error / DF Error

• F = If the calculated F-value is greater than the F-value from the F-distribution, then at least one of the coefficients is not equal to zero. The F-value is used to determine the p-value.

F-value = MS Regression / MS Error

• Residuals = The difference between the observed values and predicted values.

SRegression =

SSResidual =

MSRegression =, where 1 = degrees of freedom

MSResidual =, where 23 = degrees of freedom

Standard error_(b) =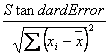

t Stat =

Figure 5. Table with all computation needed to make the regression model

* Advertising expenditures (bn pounds in current prices)

**GDP in total expenditures (bn pounds)

4.d) Testing the Regression model

There are several methods used to test the accuracy of the model, among which the simplest one is to look at the P- value in the ANOVA table (Figure 4) which is 1.9216*10^-10 , obviously smaller than 0.05 degrees of freedom meaning that the model is correct.

As well, by comparing F value with F table (from the statistical tables), it can be proven the correctness of the model since F value > F table, with the values of 162.233917 > 4.4138734.

4.e) Testing the linear relationship between the two variables

In order to verify if between UKs GDP by expenditure and the total advertising expenditures really is a linear relation, comparing t Stat value and the t table (from the statistical tables) and, as we see, 12.7371079 > 2.10092204, therefore between the 2 variables is a linear relationship.

Conclusion

The regression model analyzed is a good proof that a countrys GDP is a top ranked indicator that influences all parts of the economy, true, in different extent but still plays a huge role in the development of some certain areas, like in the given example.

Its been demonstrated that by choosing UKs GDP as independent variable and the countrys advertising expenditures as dependent one, a positive linear relationship is established, and we have the formula to sustain that evidence:

Y= 1.2506 + 0.000004*x

This will be useful for future predictions of UKs advertising expenditures, in a faster way now just by looking at the countrys GDP in the year needed.

ANEXES