| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
DETERMINANTS
1. INTRODUCTION.
Le point de départ de notre étude est le suivant :
Soit E un K-espace vectoriel de dimension
finie n rapporté à une base B et S=(v1,
., vn)
un systÃme de n vecteurs de E
définis par leurs composantes dans la base B . On a déjà étudié des techniques
de détermination du rang par des manipulations sur la matrice représentant S
dans B .
En particulier la méthode du pivot de Gauss nous ramÃne à une
matrice triangulaire équivalente, de rang n
si et seulement si aucun des coefficients diagonaux nest nul.
Il est alors naturel de se demander sil est possible de construire en marge de
cette démarche une expression
synthétique portant sur les composantes initiales des vecteurs de S et dont
lanalyse permettrait de déterminer simplement si S est à son
tour une base de E.
(On peut penser au produit des éléments de la diagonale de la matrice
triangulaire obtenue)
Bien sÃr on aimerait que lexpression en question ne dépende que des
composantes initiales des vecteurs de S, et non pas de la suite de
manipulations exécutée.
On va voir que la réponse est positive mÃme sil faudra nuancer le
qualificatif simple concernant les calculs à effectuer. Par contre le
champ dapplication de ces déterminants dépassera trÃs vite lobjectif
premier , on les mettra à profit pour linversion des matrices, la
résolution des systÃmes linéaires, la théorie de la diagonalisation,
dans les situations de la géométrie Euclidienne généralisée (orientation de
lespace, classification des isométries).
Il sagit donc dun outil extrÃmement riche mais dont la définition est
un peu délicate à mettre en place. En effet si sur le plan théorique on
ne fait que reprendre et améliorer dune certaine maniÃre les idées de
la méthode de Gauss, sur le plan pratique on est confronté à des
problÃmes de notations quelquefois assez lourdes à gérer.
Aussi nous commencerons dans cette introduction à examiner la situation
sur des espaces de petite dimension.
_ Pour n=1 le problÃme est
vite réglé.
Soit B =(e1) base dune droite vectorielle E. Le systÃme S
réduit au seul vecteur v1=xe1 est libre si et seulement
si v1 est non nul cest
à dire si x ¹0.
On appelle alors déterminant de S dans la base B la quantité detB (v1)=x.
_ Pour n=2.
Considérons un systÃme S=(v1,
v2) de deux vecteurs de E
exprimés dans la base B =(e1, e2)
suivant : v1=xe1+ye2 et v2=xe1+ye2.
a) Si x est non nul, la séquence ![]() transforme la matrice
représentant S dans B en la forme triangulaire
transforme la matrice
représentant S dans B en la forme triangulaire 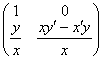 .
.
S sera alors libre si et seulement si la quantité xy-xy est non nulle.
b) Si x est nul et x différent de 0, un raisonnement
symétrique en échangeant les deux vecteurs donne : S libre xy-xy ¹ xy-xy ¹0
c) Enfin si (x, x)=(0, 0) , les deux vecteurs de S sont multiples du mÃme
vecteur e2 et constituent
donc un systÃme lié. Remarquons que dans ce cas xy-xy=0.
On définira donc naturellement ici le déterminant de S dans la base B comme lélément de K
noté et représenté par : detB (S)=xy-xy=![]()
Ce qui précÃde établit léquivalence entre la dépendance linéaire de S
et lannulation de son déterminant.
_ Pour n=3.
Soit B =(e1, e2,
e3) base de E et S=(v1, v2, v3)
systÃme dont la matrice représentative dans B est A=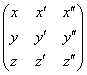 .
.
_ Si x non nul on effectue les
manipulations sur colonnes suivantes :
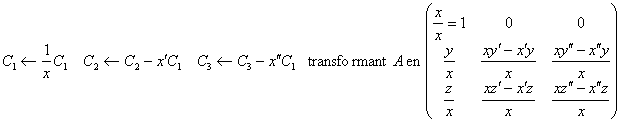
Cette matrice est donc de rang 3 si et seulement si ses deux derniÃres
colonnes forment un systÃme libre, ou encore, vu létude précédente appliquée dans le plan
engendré par (e2, e3 ), si le déterminant D=![]() est non nul.
est non nul.
_ Si x est nul mais quune des deux
composantes x ou x est différente de 0, un raisonnement
analogue en permutant v1
et v2 ou v1 et v3 aboutit à la mÃme caractérisation de lindépendance
du systÃme.
_ Enfin si x=x=x=0, les trois
vecteurs de S sont combinaisons du mÃme systÃme (e2, e3 ) donc forment un systÃme lié par application
du théorÃme fondamental de la dimension.
Remarquons que dans ce cas lexpression D ci dessus est nulle.
On définira donc ici le déterminant de S dans la base B comme la quantité D apparaissant dans cette étude. AprÃs calculs
et regroupements adéquats on peut donner de D les expressions suivantes :
D=![]() . (Développement dit
suivant la premiÃre colonne)
. (Développement dit
suivant la premiÃre colonne)
D=![]()
RÃgle dite de Sarus que lon retient en comptant positivement les
produits des termes des diagonales descendantes et négativement les produits
des termes des diagonales ascendantes dans la matrice de Sarus : 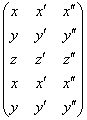
2) FORMES MULTILINEAIRES ALTERNEES.
A)
Vers une généralisation.
Il est facile de déceler des propriétés algébriques communes aux trois
déterminants que nous avons défini précédemment.
_ Il sagit dapplications f allant
de En vers K. (A tout systÃme S de n vecteurs de E on associe un scalaire f(S)
)
_ Ces applications agissent de maniÃre linéaire sur chacun des
vecteurs composant le systÃme S, les n-1 autres vecteurs étant fixés.
(Propriété dite de multilinéarité)
Par exemple pour le déterminant dordre 3 considéré comme fonction de v1 seul, les vecteurs v2 et v3 étant figés, on obtient une application K-linéaire de E vers K dont la matrice dans le couple de base (B , ) est ![]()
_ Pour n ³2 , léchange de deux vecteurs du
systÃme S transforme limage f(S) en lopposé de sa valeur. (Propriété
dite dalternance : ![]() )
)
La vérification est également immédiate sur les formules établies plus haut.
Ces traits communs nous suggÃrent la définition générale suivante, pour n ³
Définition : Si E est un K espace de dimension n , on appelle forme n-linéaire
alternée sur E toute application f de
En vers le corps K satisfaisant aux propriétés décrites
précédemment de linéarité par rapport à chacune des n variables constituant le systÃme S et dalternance.
B)PremiÃres
remarques.
Si f est n linéaire, alors f sera alternée si et seulement si f sannule sur tout systÃme S dont deux des composantes vectorielles sont identiques.
Rappelons que les corps considérés sont supposés de caractéristique nulle, donc
quen particulier : 1K ¹ -1K . (2.1k ¹0K)
_ Supposons f alternée et considérons
un systÃme S=(v1,
,
vn) tel que vi=vj pour un
couple dindices distincts.
La permutation de ces deux vecteurs au sein de S laisse donc S invariant, mais
daprÃs lalternance doit changer f(S) en son opposé.
On a donc nécessairement f(S)=-
f(S) doà lon tire 2f(S)=0K
, cest à dire (1K+1K) f(S)=0K.
On en déduit alors f(S)=0K vu lhypothÃse
2.1K ¹0K.
_ Réciproquement si f(S) sannule
dÃs que 2 vecteurs de S sont égaux, considérons deux indices distincts i <j et à partir dun élément quelconque S de En définissons les 4 systÃmes déduits chacun de S
par les manipulations suivantes :
S(i, j) obtenu par ![]()
Si obtenu par ![]()
Sj obtenu par ![]()
S obtenu par ![]()
En faisant jouer la linéarité par rapport à chacune des deux variables
dindice i et j, on écrit la décomposition : f(S(i,
j))= f(Si)+ f(S)+ f(S)+ f(Sj).
Or f sannule par hypothÃse
sur les systÃmes S(i, j), Si et Sj
admettant chacun deux composantes identiques.
Il reste donc légalité f(S)=-
f(S) exprimant lalternance de f
dans léchange des composantes dordre i
et j.
2) Une forme n-linéaire alternée
sannule nécessairement sur tout systÃme lié.
En effet si S est lié, un des vecteurs de S pourra sécrire comme combinaison
linéaire des autres. Si ![]() on en déduit par
linéarité de f par rapport à
la variable dordre i et en utilisant
les notations précédentes, la relation : f(S)=
on en déduit par
linéarité de f par rapport à
la variable dordre i et en utilisant
les notations précédentes, la relation : f(S)=![]() =0
=0
(f sannule sur chacun des Sj dont les composantes
dordre i et j égalent vj)
On a donc bien là une piste pour la caractérisation qui nous préoccupe : une forme n-linéaire alternée f permet de conclure la liberté dun systÃme S dont limage f(S) est non nulle.
Subsistent deux interrogations essentielles :
_ Quen est-il de la réciproque : (
S libre Þ
f(S)¹0 ) ?
_ Comment définir de telles formes sur un espace de dimension finie quelconque n et quel est léventail des
constructions possibles.
Les réponses vont nous Ãtre données par le théorÃme fondamental
suivant, véritable clef de tout le chapitre.
C)
ThéorÃme dexistence des déterminants.
Soit n
un entier supérieur ou égal à 2 et B une base dun K-espace vectoriel E de dimension n
Il existe une et une seule forme n-linéaire alternée f sur E prenant la valeur 1K sur la base B . et toutes les autres formes n- linéaires alternées sur E sont des
multiples de celles ci par un élément de K.
( Lapplication f sera appelée
déterminant dans la base B et notée detB
Nous allons procéder par récurrence forte sur lentier n.
_ Examinons le cas initial n=2. Avec
les notations précédentes, si f est
bi-linéaire alternée on pourra écrire : ![]()
Soit, en utilisant lalternance : ![]()
On voit donc que f est nécessairement
multiple du déterminant dordre 2 défini dans le paragraphe dintroduction et
dont les caractÃres de multi-linéarité et dalternance se vérifient
immédiatement.
La condition f(B
)=1K donne effectivement pour f(S)
la valeur xy-xy, ce qui assure la cohérence de
lappellation déterminant pour cette valeur 2.
_ Pour n=3 la tri-linéarité et lalternance
de f permet de mÃme de réduire
le calcul de f(S) à:
f(S)= f(xe1+ye2+ze3, xe1+ye2+ze3, xe1+ye2+ze3)=xyzf(e1, e2, e3)+xzyf(e1, e3, e2)
+
yxzf(e2, e1,
e3)+yzxf(e2, e3, e1)+zxyf(e3, e1, e2)+zyxf(e3, e2,
e1).
Soit en utilisant à nouveau lalternance pour retrouver dans chaque cas
limage de la base ordonnée initialement :
f(S)=[xyz+yzx+zxy-yxz-xzy-zyx ] f(e1,
e2, e3)
Ici aussi on retrouve les multiples des déterminants dordre 3 définis dans
lintroduction et précisément le déterminant dans la base B si on impose la condition f(B
)=1K.
_ Etude de lhérédité de la propriété étudiée.
Soit n
un entier supérieur ou égal à 3. Nous ferons lhypothÃse que le
théorÃme est valable pour tout entier inférieur ou égal à n et nous allons essayer den déduire
lextension de ce résultat au rang n+1.
Pour faciliter la rédaction introduisons les notations suivantes :
_ B =(e1,
.., en,
en+1) la base
de E en question dans le théorÃme.
_ Pour chaque indice i de :
Ei désigne la somme directe des droites
vectorielles engendrées par les vecteurs de B distincts de ei a![]() . Bi est la base de Ei
obtenue en supprimant ei de
B , les autres vecteurs de B restant dans lordre initial.
. Bi est la base de Ei
obtenue en supprimant ei de
B , les autres vecteurs de B restant dans lordre initial.
qi est la projection
vectorielle sur Ei parallÃlement
à la droite engendrée par ei.
_ Pour chaque couple (i,
j) dindices distincts de :
E(i, j) est la somme vectorielle des droites engendrées par les
vecteurs de Bi distincts de ej
B (i, j) est la base de E(i,
j) obtenue en éliminant le vecteur ej de la base Bi , les autres vecteurs de Bi restant dans lordre initial.
Enfin x(i, j) est le terme générique de la matrice A représentant le
systÃme S=(v1,
,vn, vn+1) dans la base B jI vj=x(1, j)e1+x(2, j)e2+
+x(n+1, j)en+1
Analyse . Si f est une forme répondant aux exigences
du théorÃme, on doit avoir nécessairement, en faisant jouer la linéarité
par rapport à la premiÃre variable, la décomposition : f(S)=![]()
Ecrivons ensuite v2=x(i, 2)ei+qi (v2). En utilisant la linéarité par rapport à la
deuxiÃme variable on peut écrire ![]() .
.
Or le premier terme de cette somme est nul en tant quimage par f dun systÃme oà deux
vecteurs sont identiques. Si on répÃte lopération pour chacune des
autres variables de S soit v3,..,
vn+1 , on obtient : f(S) =![]()
Considérons alors pour chaque indice i
lapplication fi de Ein
vers K définie par la formule :
fi (w1, w2,
,wn)=f(ei ,w1,w2,
,wn).
_ On voit immédiatement que la multi-linéarité de f entraine la linéarité de fi
par rapport à chacune de ses n
variables.
_ Il est aussi clair que fi
sannule sur tout systÃme dont deux des vecteurs sont identiques, ceci
daprÃs lalternance de f.
DaprÃs lhypothÃse de récurrence, fi est donc multiple du déterminant dans la base Bi que nous noterons de maniÃre abrégée deti , en tant que forme n-linéaire alternée sur lespace Ei de dimension n.
La constante multiplicative nest autre que le scalaire ai =f(ei
,Bi ) daprÃs la
spécification deti (Bi )=1K
Examinons cette constante. Il sagit de limage par f dun systÃme formé par les vecteurs de la base initiale B , listés en désordre par rapport
à lagencement initial, sauf bien sÃr pour i=1.
ai =f(ei
,Bi )=f (ei
, e1,
,ei-1, ei+1,
,en+1)
Pour retrouver lordre initial, il suffit déchanger successivement le vecteur
décalé en tÃte ei
avec chacun des i-1 vecteurs le
suivant, soient e1, e2,
., ei-1.
A chacune de ces transpositions élémentaires, la valeur de f est changée en son opposée, toujours daprÃs lalternance
de f. On obtient donc à
terme : ai =(-1)i
1f(B )
Ainsi une forme n+1 linéaire alternée
f sur E de dimension n+1 est nécessairement définie par une
formule du type :
![]()
avec a=f(e1,
.,en+1).et deti désignant rappelons le, le déterminant dans
la base Bi de
Ei.
SynthÃse. Reste
à vérifier que lapplication f
définie comme précédemment avec a=1K est bien effectivement n+1 linéaire alternée. Elle sera alors
le déterminant dordre n+1 dans la
base B de E dont toutes les formes n+1
linéaires alternées sur E sont effectivement multiples.
a) La multilinéarité est facile à prouver.
_ Pour létablir par rapport à la premiÃre variable v1, il suffit de remarquer
que si v2,
,vn+1 sont fixés,
les quantités bi=(-1)i
1deti (qi (v2),
, qi
(vn+1)) sont
constantes et donc que lapplication v1
a f(v1,
.vn+1) est une
forme linéaire sur E dont la matrice dans le jeu de bases (B , (1K)) nest autre que la
ligne L=![]()
_ Pour la linéarité par rapport à la variable dordre j ¹1, remarquons que qi étant linéaire (projecteur de lespace E) et deti étant linéaire par rapport
à la variable dindice j-1,
lapplication vj a bi=(-1)i 1deti
(qi (v2),
,qi(vj ),
, qi (vn+1)) sera linéaire pour chaque i daprÃs le théorÃme de
composition.
Les composantes x(i, 1) étant ici constantes car v1 fixé, lapplication vj a
f(v1,..,vj ,..,vn+1)
est bien linéaire comme combinaisons de formes linéaires sur E.
b) Pour lalternance.
La multilinéarité étant établie, on sait quil suffit de montrer lannulation
de f sur tout systÃme
comportant deux vecteurs identiques.
_ Cela est évident si ces deux vecteurs sont dindice distinct de 1, car dans
ce cas chacun des bi sera nul par alternance de deti .
_ Si un des deux indices en question est 1, en utilisant le résultat précédent
on pourra toujours se ramener au cas oà le second indice est 2. Reste
donc à montrer que f sannule
si v1=v2.
Pour cela développons chacun des bi comme nous lavons
fait initialement sur f dans
lanalyse précédente en faisant jouer la linéarité par rapport à chacune
des variables et lalternance.
Il vient, en utilisant les notations précisées tout au début :
bi=![]()
Or pour chaque couple (i, j) avec i¹j, lapplication g(i, j) définie sur E(i,
j)n-1
par la formule :
![]() est de maniÃre
évidente une forme n-1 linéaire
alternée.
est de maniÃre
évidente une forme n-1 linéaire
alternée.
(Les propriétés de la forme n
linéaire alternée deti se
répercutent immédiatement sur g(i, j) g(i, j) est donc par hypothÃse de
récurrence un multiple du déterminant dans la base B(i, j).,
le coefficient multiplicatif nétant autre que deti (ej
, B(i, j)).
Etudions ce scalaire suivant les positions relatives de i et j.
_ Si j >i deti (ej , B(i, j))=![]()
Il sagit donc de limage par le déterminant dans la base Bi dun systÃme de vecteurs
qui nest autre que ceux de cette mÃme base Bi mais listés en désordre par
rapport à la situation initiale.
Pour retrouver cet ordre originel il suffit déchanger successivement le
vecteur en tÃte ej
avec chacun des j-2 vecteurs e1,
,ej-1 précédant
ej+1.
Vu lalternance de deti on
obtient donc à terme lexpression : deti (ej , B(i,j))=(-1)j-2.
_ Si j <i deti (ej , B(i, j))=![]()
Ici j-1
transpositions élémentaires seront nécessaires pour amener ej à sa bonne place dans la base Bi . On aura alors deti (ej , B(i,j))=(-1)j-1. Ainsi
lexpression de f(S) peut se décomposer :
![]()
Puisque par hypothÃse v1=v2 , lexpression précédente
peut sécrire S1+S2 avec :
S1 la somme des ![]() correspondant aux
couples de T1=
correspondant aux
couples de T1=
S2 la somme des 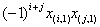 correspondant aux
couples de T2=
correspondant aux
couples de T2=
T1 étant en bijection avec T2 par la correspondance (i,
j) a(j, i) , il est facile den déduire
légalité S2=-S1
Ainsi on a bien vérifié que f
sannule sur S pour lequel les deux premiers vecteurs coÃncident, ce qui
achÃve la démonstration.
D)
Conséquences.
1) Application à létude de
lindépendance dun systÃme.
Comme premiÃre conséquence de ce théorÃme nous pouvons
maintenant énoncer la caractérisation complÃte de lindépendance
linéaire pour un systÃme de n
vecteurs.
Si S est un systÃme de n vecteurs au sein dun K-espace E de dimension n et si B désigne une base quelconque de E, on a toujours léquivalence : S libre detB (S) ¹
_ On savait déjà que le déterminant dans B sannule sur tout systÃme lié et donc que S est libre si son
déterminant dans B est non nul.
_ Réciproquement, supposons S libre, donc base de E car son cardinal
coÃncide avec la dimension de cet espace.
Le déterminant dans S est alors une forme n-linéaire
alternée sur E qui est donc multiple du déterminant dans B par un scalaire a daprÃs le
théorÃme fondamental.
(a nétant autre que le déterminant
de B dans S)
En particulier on peut écrire 1K=detS(S)=adetB (S) et par suite le déterminant dans B de S est non nul.
2) Formule du changement de base.
Notation quotient.
Si B et B sont deux bases du K-espace E, le théorÃme fondamental montre que le
déterminant dans B est égal au produit du déterminant dans B par le scalaire a qui nest autre que le
déterminant de B dans B .
(Cest le schéma que lon a appliqué ci dessus au couple (B ,S) ).
Cette formule de passage est plus commode à écrire et à mémoriser
si on utilise la notation dite quotient dans laquelle on écrira ![]() pour désigner le
déterminant de S dans B.
pour désigner le
déterminant de S dans B.
On rencontre aussi la version ![]() .
.
La proportionnalité se traduit alors par la relation : Pour tout
systÃme S de n vecteurs de E
![]() ou par
ou par ![]()
On en déduit en particulier en prenant S=B2 que les déterminants ![]() et
et ![]() sont inverses lun de
lautre.
sont inverses lun de
lautre.
3) Inversibilité dune matrice
carrée.
Si A est un élément de Mn(K), son rang est celui du systÃme S de ses n vecteurs
colonnes considérés comme vecteurs de E=Kn décomposés dans la base canonique B de cet espace.
DaprÃs le théorÃme fondamental on peut donc dire que A est de rang n, ou encore est inversible, si et seulement si le déterminant de S dans B est non nul.
Ce déterminant sera appelé naturellement déterminant de la matrice A et est noté det(A).
Lintervention de cette notation permet de formuler de façon plus pratique la
relation de définition par récurrence des déterminants généraux.
En effet le déterminant dordre n
noté dans la démonstration :![]()
nest autre que le déterminant de la matrice carrée Ai obtenue à partir de A en supprimant la premiÃre colonne et la ligne dindice i.
La construction se résume alors à : ![]()
Formule dite du développement suivant la premiÃre colonne de A.
4) Déterminant dun endomorphisme.
Soit u un endomorphisme dun K-espace vectoriel E de dimension n et B
une base de E.
On vérifie trÃs facilement que lapplication de En vers K définie par :
S=(v1,
.,vn)
a ![]() avec u(S)=(u(v1),
.,
u(vn))
, est une application n-linéaire
alternée donc est multiple du déterminant dans la base B. Le coefficient multiplicatif sera le scalaire
avec u(S)=(u(v1),
.,
u(vn))
, est une application n-linéaire
alternée donc est multiple du déterminant dans la base B. Le coefficient multiplicatif sera le scalaire ![]() cest à dire le
déterminant de la matrice A
représentant u dans la base B.
cest à dire le
déterminant de la matrice A
représentant u dans la base B.
Pour tout systÃme S on a donc
la relation a (1) ![]()
Examinons linfluence dun changement de base. Si on repÃre maintenant
lespace E à laide dune nouvelle base B, on sait que le déterminant dans B dun systÃme quelconque sobtient en multipliant le
déterminant dans B de ce mÃme
systÃme par la constante a=![]()
En multipliant par a les
deux termes de légalité précédente (1) on obtient alors :
Pour tout systÃme S de n vecteurs de E : ![]()
En prenant S=B on en déduit que det(A)=det(A) avec A matrice
représentant u dans B.
Le déterminant de la matrice A
représentant initialement u nest
donc pas affecté par le changement de base effectué. Il sagit dun invariant,
au mÃme titre que la trace de la matrice, cest une constante attachée
à lendomorphisme u et que
lon appellera donc naturellement déterminant de cet endomorphisme. (notation det(u) )
La caractérisation : A matrice carrée inversible det(A) ¹0 se
traduit alors par :
lendomorphisme u est bijectif det(u)
¹0 .
La relation de proportionnalité (1) se transcrit alors simplement : Pour
tout élément S de En
et
toute base B de E on a légalité ![]()
5) Déterminant dun produit.
DaprÃs ce qui précÃde, si u
et v sont deux endomorphismes de E et
B une base de cet espace, on peut
écrire : det(v![]() u)=
u)=![]()
Le déterminant dun composé est donc le produit des déterminants. det(v![]() u)=det(v).det(u)
u)=det(v).det(u)
Lapplication de LK(E) vers K qui à chaque endomorphisme associe son déterminant
est donc un morphisme de la loi ![]() vers la loi produit
dans K.
vers la loi produit
dans K.
Comme on a vu que u était inversible
si et seulement si det(u) ¹0, lapplication u adet(u)
apparait comme un morphisme du groupe ( GLK(E),![]() ) vers le groupe multiplicatif (K-, . )
) vers le groupe multiplicatif (K-, . )
On retrouve ainsi en particulier det(IE)=1K
et uI GLK(E) : ![]()
6) Inversion dun automorphisme.
Soit u un automorphisme de E de
matrice représentative A dans la base
B.
Pour tout vecteur y de E, u-1(y)=x y=u(x)
On va voir que la théorie des déterminants permet dexpliciter facilement les
coordonnées de lantécédent x de y à partir de celles de y.
Posons ![]() . Par linéarité de u
il vient :
. Par linéarité de u
il vient : ![]() .
.
Notons alors S le systÃme
image ![]() et pour chaque indice i de désignons par S(i,
y) le systÃme obtenu à partir de S en remplaçant le vecteur u(ei) par y.
et pour chaque indice i de désignons par S(i,
y) le systÃme obtenu à partir de S en remplaçant le vecteur u(ei) par y.
Notons enfin S(i,
j) le systÃme obtenu
toujours à partir de S en
remplaçant u(ei) par u(ej)
DaprÃs la linéarité du déterminant dans B par rapport à la variable dindice i on peut écrire la décomposition : ![]()
Or S(i, j) est un
systÃme dont les composantes vectorielles dindice i et j sont identiques,
son déterminant dans B sera donc nul
pour i ¹j daprÃs la propriété
dalternance.
Le seul terme non nul de la somme précédente est donc celui dindice j=i. Remarquons alors que S(i, i) nest autre
que le systÃme initial S dont
le déterminant dans B est, par
définition, le déterminant de lautomorphisme u.
On en déduit la relation : iI : 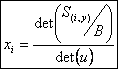
Ces formules exprimant les coordonnées de lantécédent x de y par u sont dites de Cramer.
On peut en donner une expression plus pratique en faisant appel à la
matrice A représentant u dans la base B.
En effet le numérateur apparait alors comme le déterminant de la matrice carrée
obtenue à partir de A en remplaçant
la colonne dindice i par la colonne
des composantes de y dans B.
Si on note A(i,y) cette
matrice, on obtient finalement : i I : 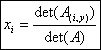
3)
TECHNIQUES DE CALCUL DES DETERMINANTS.
Pour linstant le seul mode de calcul à notre disposition est la formule
dite du développement suivant la premiÃre colonne, qui nous a servi
à établir le théorÃme fondamental.
On va voir dans ce paragraphe quil existe dautres techniques dévaluation,
générales comme le développement suivant une colonne ou une ligne quelconque,
ou adaptées à des configurations particuliÃres (matrices
triangulaires, ou matrices définies par blocs).
La connaissance de ces méthodes nest pas indispensable, surtout depuis lessor
des logiciels de calcul formel, mais permet souvent de conduire plus
efficacement le développement ou la factorisation des déterminants étudiés.
Elle aide aussi sur le plan théorique à renforcer la compréhension de la
transposition des matrices.
Les notations seront celles développées dans la démonstration du
théorÃme fondamental.
S systÃme de n vecteurs vj de E représenté dans la base B par la matrice A de
coefficient générique x(i,
j)
A)
Développement suivant une colonne quelconque.
Nous
écrirons ici simplement det pour parler du déterminant dans la base B.
Soit jI. Echangeons successivement le vecteur vj de S avec
chacun des j-1 vecteurs le précédant
au sein de ce systÃme. On obtient à terme un nouveau
systÃme S tel que, vu la
propriété dalternance : det(S)=(-1)j-1det(S).
Remarquons dabord que la matrice A
représentant S dans B est obtenue en portant en tÃte
la colonne dindice j, les autres
colonnes restant dans lordre initial.
Supprimer la premiÃre colonne de A
revient donc à supprimer la colonne dindice j de A.
Développons alors le déterminant de S
suivant la premiÃre colonne.
det(S)=![]() , avec pour Ai la matrice carrée dordre
n-1obtenue à partir de A en supprimant la premiÃre
colonne et la ligne dindice i.
, avec pour Ai la matrice carrée dordre
n-1obtenue à partir de A en supprimant la premiÃre
colonne et la ligne dindice i.
Vu la remarque faite ci dessus, Ai =A(i, j) avec A(i, j) matrice
dordre n-1 obtenue à partir
de A en supprimant la colonne dordre
j et la ligne dindice i.
Comme (-1)j 1.(-1)i 1=(-1)i+j , on obtient la formule
de développement suivant la colonne j :
![]()
B)
Développement suivant la premiÃre ligne.
Considérons lapplication f de En vers K qui à tout systÃme S représenté par A dans B fait correspondre le scalaire ![]() , avec A(1, j) désignant comme précédemment la
matrice dordre n-1 obtenue en
éliminant de A la premiÃre
ligne et la colonne dindice j.
, avec A(1, j) désignant comme précédemment la
matrice dordre n-1 obtenue en
éliminant de A la premiÃre
ligne et la colonne dindice j.
Montrons que f est n-linéaire alternée.
_ Linéarité par rapport à la
variable dordre k.
a Pour j ¹k le coefficient x(1, j) est
figé et le déterminant de A(1, j) dépend linéairement du vecteur vk de S .
En effet det(A(1, j))=det(q1(Sj))
avec pour Sj le
systÃme obtenu en supprimant
de S le vecteur vj et q1 la projection définie
par : x1e1+
.+xnen ax e +
+xnen
, le déterminant étant évalué dans la base B1
=(e2,
,en).
a Pour j=k. cest le déterminant de A(1,
k) qui est alors figé, puisque
la colonne représentant la composante variable vk a été éliminée. Par contre le coefficient x(1, k) premiÃre composante de vk dans B
dépend linéairement de ce vecteur vk.
_ Alternance.
Supposons que vl=vk pour l <k.
Les matrices A(1, j) ont donc deux colonnes
identiques pour j et sont donc de
déterminant nul. Il reste donc f(S)=(-1)l+1x(1,
l)det(A(1, l))+(-1)k+1x(1, k)det(A(1, k))
Examinons ces deux déterminants résiduels.
Si on note C1,C2,,Cn les colonnes de A
privées du coefficient relatif à la premiÃre ligne on a :
det(A(1,
l))=det(C1,C2,
,Cl-1,Cl+1,
Ck-1,Ck
.,Cn)
det(A(1,
k))=det(C1,C2, ,Cl-1,Cl ,
,Ck-1,Ck+1,
.,Cn)
On passe donc puisque Cl=Ck de la premiÃre
matrice à la seconde en échangeant successivement la colonne Ck avec chacune des k-l-1 colonnes la précédant.
Vu lalternance, on en conclÃt : det(A(1, k))=(-1)k-l-1det(A(1,
l)) et par suite f(S)=0
puisque les coefficients x(1, l) et x(1, k)
coÃncident.
DaprÃs le théorÃme fondamental il existe donc un scalaire a tel que pour tout systÃme
S on ait la relation de
proportionnalité : f(S)=adet(S)=adet(A).
Or pour S=B on trouve A=In
et de maniÃre évidente f(B)=1.det(In-1)=1
Ainsi a=1
et f
coÃncide avec le déterminant dans la base B sur tout systÃme S.
On a donc une formule de développement dune matrice carrée suivant la
premiÃre ligne analogue à celle du développement suivant la
premiÃre colonne.
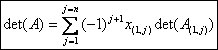
(avec A(1, j) déduite de A par
suppression de la premiÃre ligne et de la colonne dindice j.)
Cette relation va jouer un rôle clef dans le théorÃme suivant concernant
le déterminant dune matrice transposée.
C)
Déterminant dune transposée.
ThéorÃme :
Le déterminant dune matrice carrée quelconque A est toujours égal à
celui de la transposée tA
La démonstration seffectue ici par récurrence sur lordre n de la matrice.
_ Pour n £3 la vérification est immédiate
en examinant les formules explicitant les déterminants correspondants.
_ Supposons la propriété vraie pour un entier n donné et considérons une matrice carrée A dordre n+1 de terme
générique a(i, j) et sa
transposée B=tA de coefficient général b(i, j)=a(j, i).
Evaluons le déterminant de B en
développant suivant la premiÃre ligne.
![]()
Or b(1, j)=a(j, 1) et B(1, j) est la
matrice obtenue en éliminant de B=tA la premiÃre ligne et la colonne
dordre j , cest à dire en
fait la transposée de la matrice A(j, 1) obtenue en supprimant de A la premiÃre colonne et la ligne
dordre j.
Par hypothÃse de récurrence on peut donc dire que : j I det(B(1, j))=det(A(j, 1))
Ainsi on obtient ![]() . Mais ceci nest
autre que la formule du calcul du déterminant de A suivant la premiÃre colonne. On a donc bien établi que le
théorÃme sétend à lentier suivant n+1 : det(tA)=det(A) pour A carrée quelconque dordre n+1.
. Mais ceci nest
autre que la formule du calcul du déterminant de A suivant la premiÃre colonne. On a donc bien établi que le
théorÃme sétend à lentier suivant n+1 : det(tA)=det(A) pour A carrée quelconque dordre n+1.
Ceci achÃve la démonstration.
Les manipulations de type Gauss sur les colonnes vont donc se traduire par des
manipulations analogues sur les lignes avec les mÃmes conséquences liées
aux caractÃres de multilinéarité et dalternance des déterminants. En
résumé :

D)
Développement suivant une ligne quelconque.
Vu le résultat sur la transposition, la formule du développement du déterminant
suivant une colonne dindice quelconque se traduit immédiatement, si on
lapplique à la transposée dune matrice donnée A, par une formule analogue dite de développement suivant une
ligne :
i I 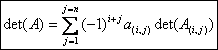
A(i, j) désignant
toujours la matrice carrée dordre n-1
obtenue à partir de A en
supprimant la ligne dindice i et la
colonne dindice j.
E)
Déterminant dune matrice triangulaire.
ThéorÃme. Le déterminant dune matrice carrée triangulaire
supérieure ou inférieure est égal au produit des éléments de la diagonale
principale.
Vu le théorÃme sur la transposée
il suffit en fait de traiter le cas dune matrice triangulaire supérieure.
Ici encore une récurrence sur lordre n
de la matrice donne facilement le résultat.
_ Pour n £3 les vérifications sont
immédiates sur les formules de calcul.
_ Supposons la propriété vraie pour un entier n et examinons une matrice triangulaire supérieure A dordre n+1 de coefficient générique a(i,
j).
En développant son déterminant suivant la premiÃre colonne, la formule
se résume en fait à :
det(A)=a(1,1)det(A(1,1))
avec pour A(1,1) la
matrice carrée dordre n obtenue en
supprimant la premiÃre ligne et la premiÃre colonne de A.
A(1,1) étant de
maniÃre évidente aussi triangulaire supérieure, son déterminant sera par
hypothÃse de récurrence le produit de ses éléments diagonaux principaux.
Ainsi det(A)=a(1,1).a(2,2)
.a(n+1,n+1)
Le théorÃme est donc bien encore vérifié pour le rang suivant n+1, ce qui termine la preuve par
récurrence.
F)
Déterminant dune matrice définie par blocs.
Toute matrice carrée M dordre n+p peut Ãtre considérée dans sa
représentation sous forme de tableau comme la juxtaposition de quatre sous
tableaux appelés blocs définis comme suit :
_ A IMn(K) formé des termes m(i, j) tels que i £n et j £n.
_ B IMp(K) formé des termes m(i, j) tels que n <i £n+p et n <j £n+p.
_ T I M(p, n)(K) formé des termes m(i, j) tels que n <i £n+p et j £n.
_ S IM(n, p)(K) formé des termes m(i, j) tels que i £n et n
<j £n+p.
On peut écrire en abrégé ![]()
ThéorÃme. Si lun des deux blocs rectangulaires T ou S
de la décomposition précédente est nul, alors le déterminant de la matrice
composée M est égal au produit des
déterminants de ses deux blocs carrés A
et B. a det(M)=det(A).det(B)
Ici encore, grace au résultat sur la transposition il suffit de traiter le cas
oà T est nul.
La démonstration seffectue alors facilement par récurrence sur n.
_ Pour n=1, il sagit simplement de
la formule du développement suivant la premiÃre colonne.
![]()
_ Si le résultat est supposé vrai pour un entier donné n (et sous-entendu pour un entier p quelconque), considérons M
dordre n+1+p décomposée en blocs comme indiqué plus haut mais avec A carré dordre n+1 et T identiquement
nul.
En développant det(M) suivant la
premiÃre colonne on obtient alors avec les notations usuelles : ![]()
Or pour chaque indice i la matrice M(i,1) peut se décomposer en blocs sous la forme :
![]() avec Si déduit de S par suppression de la ligne dindice i.
avec Si déduit de S par suppression de la ligne dindice i.
DaprÃs lhypothÃse de récurrence on peut donc écrire det(M(i,1))=det(A(i,1)).det(B) et par suite
![]() soit encore det(M)=det(A).det(B).
soit encore det(M)=det(A).det(B).
Lhérédité du principe de calcul est donc vérifiée, ce qui achÃve la
preuve par récurrence.
Déterminants. Exercices.
Exprimer
sous forme de produits de facteurs élémentaires les déterminants :
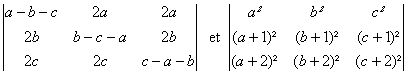
Montrer
que les déterminants suivants sont des polynômes de la variable x et déterminer leurs racines :
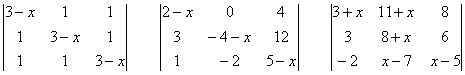
Factoriser
les déterminants suivants :
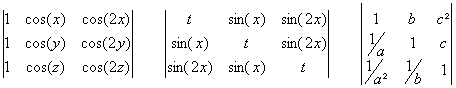
On considÃre la matrice 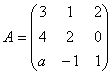 avec a paramÃtre réel.
avec a paramÃtre réel.
Déterminer les valeurs de a pour
lesquelles A est inversible et
exprimer dans ce cas A-1
en utilisant les formules de Cramer.
On
considÃre la matrice à coefficients réels 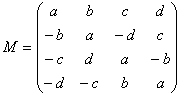
Examiner le produit tM.M . Que peut on en déduire au sujet du
déterminant de M ?
Factoriser
le déterminant : 
Montrer que tout endomorphisme f dun plan vectoriel E satisfait toujours à la relation dite de Cayley-Hamilton : f 2-trace(f).f + det(f).IE=0
Calculer
le déterminant de la matrice carrée A
dordre n dont tous les coefficients
sont égaux au scalaire a exceptés les
termes de la diagonale principale prenant tous la valeur x.
On
considÃre les deux matrices 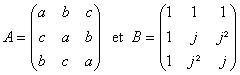 avec
avec ![]() racine cubique de
lunité. Examiner le produit AB puis
en déduire une expression factorisée du déterminant de la matrice A.
racine cubique de
lunité. Examiner le produit AB puis
en déduire une expression factorisée du déterminant de la matrice A.
On considÃre le polynôme ![]()
Montrer que P(X) peut sinterpréter comme le déterminant de la matrice carrée A dordre n+1 définie comme suit :
_ La premiÃre ligne est formée des coefficients du polynôme, listés dans
lordre des degrés décroissants, soit : an , an-1,
..,
a1, a0.
_ La ligne dordre i >1 a son coefficient diagonal égal
à X, son terme dindice
colonne i-1 égal à 1, et tous
les autres coefficients nuls.
Soit S=(a1, a2,
.., an) un systÃme de n réels donnés.
Calculer le déterminant de la matrice carrée M dordre n dont la ligne
dindice i quelconque est définie
comme suit :
_ Les i premiers coefficients sont
tous égaux à ai..
_ Les n-i termes suivants sont, dans
lordre initial, les n-i derniers
termes du systÃme S.
Par exemple : L3=( a3, a3, a3,
a4, a5,
..,an
)
Déterminants bordants.
B=(e1,
., en)
désigne une base dun K-espace vectoriel E.
On note pour chaque i de , pi
la projection sur la droite
engendrée par ei
parallÃlement à lespace Ei
engendré par les vecteurs de B
distincts de ei.
Soit k est un entier fixé strictement
inférieur à n. On note q=p1+p2+
..+pk la projection sur VecK(e1,
,ek) parallÃlement à VecK(ek+1,
,en)
On considÃre enfin un systÃme S=(v1,
.., vk) de k
vecteurs de E tel que son image par q
soit un systÃme libre.
Montrer quun vecteur quelconque w de
E appartient au sous-espace engendré par S
si et seulement si chacun des n-k
déterminants suivants ![]() dordre k+1 est
nul :
dordre k+1 est
nul :
i I ![]() désigne le déterminant
dans la base Bi= (e1,
,ek ,ei
) du systÃme
désigne le déterminant
dans la base Bi= (e1,
,ek ,ei
) du systÃme
Si=(q(v1)+pi(v1),
., q(vk)+pi(vk),
q(w)+pi(w) )
Déterminant de Vandermonde.
A tout systÃme S=(x1,
., xn) de n
scalaires (n ³2) on associe le déterminant Dn dordre n de la matrice A de coefficient générique a(i,
j)=(xi)j-1
Etablir par récurrence sur lentier n
la formule : ![]()
Déterminant fonction dune
variable réelle.
On note D(x) le déterminant de la matrice carrée A(x) dordre n dont le coefficient générique dindice
ligne i et colonne j est a(i, j)(x) avec a(i,
j) fonction définie sur un
intervalle I de R à valeurs dans R. (Fonctions dites composantes).
a) Montrer que si chacune des fonctions composantes est continue sur I, alors
la fonction
x aD(x) est aussi continue sur I.
b) Montrer que si les fonctions composantes sont toutes dérivables sur I, D se dérive sur I par addition des n
déterminants obtenus en remplaçant successivement chacune des colonnes de la
matrice A(x) par celle des dérivées des fonctions la composant.
Dérivée dun déterminant.
Les notations sont celles de lexercice précédent.
a) On note O(h) une matrice carrée
dordre n dont les coefficients sont
des fonctions composantes négligeables devant h en 0. Montrer que pour toute matrice carrée A dordre n à
coefficients indépendants de h, on a
au voisinage de 0 : det(A+O(h))=det(A)+o(h)
b) En déduire, toujours au voisinage de 0 : det(In+h.A+O(h))=1+trace(A).h+o(h)
c) Si toutes les fonctions composantes de la matrice A(x) sont dérivables et
si A(x) est inversible quelque soit x
de lintervalle I, déduire de ce qui précÃde la formule de
dérivation : ![]()
Soit A IMn(K) et ![]() . On construit à partir delles la matrice C de M2n(K) définie par blocs suivant le
schéma :
. On construit à partir delles la matrice C de M2n(K) définie par blocs suivant le
schéma : ![]()
Montrer que det( C)=(det(A))².(det(B))n
(On pourra faire apparaitre un carré inférieur dordre n nul afin dappliquer le principe de calcul du déterminant par
blocs)
Soit N une matrice carrée dordre n
nilpotente.
a) Montrer que N est semblable à une matrice triangulaire supérieure dont
tous les éléments diagonaux sont nuls. On pourra procéder par récurrence sur
lordre de nilpotence de N cest
à dire le plus petit entier k
tel que N k=0.
b) En déduire que pour une telle matrice on a det(In+N)=1.
c) Soit N nilpotente et A une matrice carrée inversible de
mÃme taille et commutant avec N
. Montrer en utilisant ce qui précÃde que det(A+N)=det(A).
Soit f un endomorphisme dun C-espace vectoriel E de dimension n tel que f 3-IE soit non injectif. Montrer quil existe un nombre complexe a tel que f-aIE soit non injectif.
Calculer le déterminant de la
matrice carrée Tn dordre n dont la ligne dindice i quelconque nest autre que la ligne
dordre i du triangle de Pascal complétée
par des zéros et privée de son dernier terme pour la derniÃre ligne .
iI j I t(i, j)=![]() et j >i+1 t(i,
j)=0
et j >i+1 t(i,
j)=0
j I t(n,
j)=![]()
Calculer le déterminant Dn de la matrice dordre n dont tous les coefficients sont égaux à 1 sauf ceux de la diagonale principale listés de haut en bas suivant la série des entiers successifs : 2, 3, , n, n+1.
Exercices sur les Déterminants. Solutions.
Convention générale : Pour simplifier la rédaction, chaque fois
quune manipulation de type Gauss conduit à la mise en facteur dun
scalaire l
dans une colonne ou une ligne, nous ne mentionnerons pas la factorisation
évidente de l
dans le déterminant étudié déduite de la multilinéarité.
Pour
le premier déterminant, les manipulations sur colonnes ![]() conduisent dabord
à
conduisent dabord
à
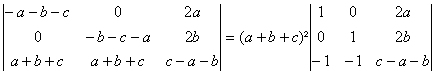
On conclut par 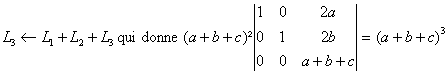
Pour le deuxiÃme on peut commencer par la séquence 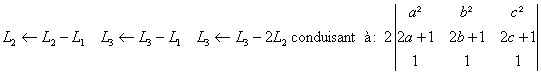
On poursuit avec 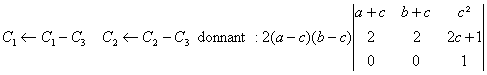 soit, en développant
suivant la derniÃre ligne :
soit, en développant
suivant la derniÃre ligne : ![]()
a)
La séquence ![]() amÃne la forme
triangulaire
amÃne la forme
triangulaire 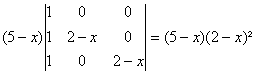
b) 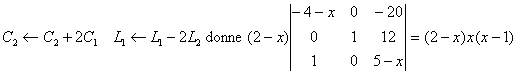
c) 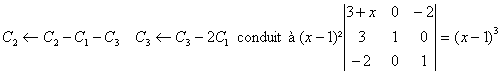
![]() conduit à la
factorisation :
conduit à la
factorisation :
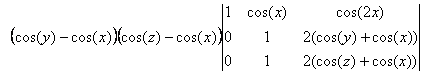 .
.
On termine en développant suivant la premiÃre colonne, ce qui
donne :
2(cos(y)-cos(x))(cos(z)-cos(x))(cos(z)-cos(y))
b) ![]() conduit à la
forme triangulaire :
conduit à la
forme triangulaire :
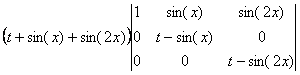 cest à dire
à la forme factorisée :
cest à dire
à la forme factorisée :
![]()
c) ![]() conduit à
lexpression :
conduit à
lexpression :
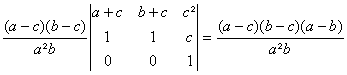
La
séquence ![]() donne det(A)=
donne det(A)=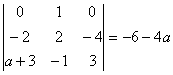
A est donc inversible si et seulement
si a est différent de ![]() .
.
On peut alors déterminer A-1
grace à léquivalence :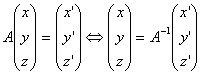
Les formules de Cramer permettent dexprimer le triplet (x, y, z) en fonction de (x, y, z):
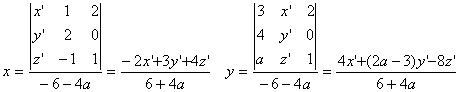
et de mÃme .
.
Ce qui donne pour inverse de A la
matrice : 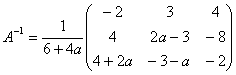
Un
calcul élémentaire donne tM.M=(a²+b²+c²+d²)I4.
On en déduit det(tM).det(M)= (a²+b²+c²+d²)4
daprÃs la rÃgle du produit,
puis (det(M))²= (a²+b²+c²+d²)4 grace au
théorÃme sur le déterminant dune transposée.
Ainsi det(M)=![]() (a²+b²+c²+d²)²
puisque les coefficients sont supposés réels.
(a²+b²+c²+d²)²
puisque les coefficients sont supposés réels.
Remarquons alors que si (b, c,
d) est un triplet donné fixé, le déterminant de M considéré comme fonction de la variable a seule est un polynôme de degré 4 de terme dominant a4.
Il suffit pour sen assurer de considérer les monômes obtenus en développant ce
déterminant suivant la premiÃre colonne.
(Plus généralement on peut montrer facilement par récurrence que si AIMn(K), la fonction
x a det(A+xIn) est un polynôme de terme dominant xn)
On en déduit finalement la relation det(M)=
(a²+b²+c²+d²)².
On
peut par exemple faire apparaitre des 0 sur la premiÃre ligne et la
premiÃre colonne grace aux manipulations :![]() puis
puis
![]() , ce qui donne
, ce qui donne 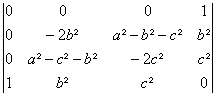
Soit en développant:![]() qui se factorise facilement en (a+b+c)(a+b-c)(b+c-a)(c+a-b)
qui se factorise facilement en (a+b+c)(a+b-c)(b+c-a)(c+a-b)
Soit
A=![]() une matrice carrée quelconque dordre 2 à
coefficients dans K.
une matrice carrée quelconque dordre 2 à
coefficients dans K.
On a immédiatement A²=![]()
Posons t=trace(A)=a+d et D=det(A)=ad-bc.
Il vient alors a²+bc=a(a+d)+bc-ad=ta-D et d²+bc=d(d+a)+bc-ad=td-D.
Ainsi on a A²=![]() =t.A-D.I2
=t.A-D.I2
Tout endomorphisme f dun plan
vectoriel E vérifie donc bien la relation de Cayley :
f
2-trace(f).f +det(f).IE=0.
Commençons
par remplacer C1 par la
somme C1+C2+
.+Cn. La premiÃre colonne est alors formée de
coefficients tous égaux à x+(n-1)a ce qui nous permet décrire
det(A)=[x+(n-1)a]det(B) avec B identique
à A sauf pour ce qui concerne
sa premiÃre colonne dont tous les termes sont maintenant égaux à
1.
Soustrayons alors la premiÃre ligne de B à chacune des n-1
lignes suivantes de B.
B est ainsi transformée en une
matrice triangulaire supérieure dont tous les termes diagonaux égalent x-a. On peut donc conclure det(A)=[x+(n-1)a](x-a)n-1
Un
calcul élémentaire donne
A.B=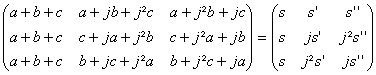 avec s, s,
s sommes définies par s=a+b+c ; s=a+jb+j²c ; s=a+j²b+jc. ( ceci daprÃs j3=1)
avec s, s,
s sommes définies par s=a+b+c ; s=a+jb+j²c ; s=a+j²b+jc. ( ceci daprÃs j3=1)
On en déduit daprÃs la rÃgle du produit et la multilinéarité du
déterminant, la relation det(A).det(B)=s.s.s.det(B).
Or le déterminant de B nest pas nul,
on obtient sa valeur rapidement en remplaçant par exemple sa premiÃre
colonne par la somme des trois, ce qui donne vu légalité classique 1+j+j²=0 :
det(B)=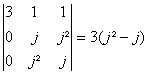
Ainsi det(A)= s.s.s=(a+b+c).(a+jb+j²c).( a+j²b+jc).
La
démonstration seffectue facilement par récurrence sur le degré n du polynôme.
_ Pour n=0 et n=1 la vérification est immédiate.
_ Supposons la propriété vraie pour tout polynôme de degré au plus n et examinons un polynôme P(X)
de degré n+1,.soit : ![]() .
.
Développons suivant la premiÃre colonne le déterminant supposé reconstituer
P(X)
selon les données de lénoncé. On obtient det(An+1)=an+1det(Tn)-(-1)det(An) avec pour Tn une matrice triangulaire
inférieure dordre n+1 dont tous les
coefficients diagonaux sont égaux à X
et An matrice
carrée dordre n+1 dont le
déterminant coÃncide, daprÃs lhypothÃse de récurrence,
avec a0+a1X+
.+anXn.
On en déduit donc bien : det(An+1)=an+1 X n+1+ a0+a1X+
.+anXn=P(X)
ce qui achÃve la récurrence.
Effectuons
sur les colonnes de la matrice donnée M
la série de manipulations suivante : ![]()
Dans chaque colonne dindice j+1 >1 les termes au dessus de la
diagonale principale sont tous égaux à aj+1-aj
et ceux sur ou en dessous de cette diagonale sont nuls.
On peut donc écrire daprÃs la multilinéarité :
det(M)=![]() , avec pour A une
matrice dordre n dont la
premiÃre colonne nest autre que celle de M et pour laquelle toute colonne dindice j >1
est formée de 1 au dessus de la diagonale principale tandis que ses autre
termes sont nuls.
, avec pour A une
matrice dordre n dont la
premiÃre colonne nest autre que celle de M et pour laquelle toute colonne dindice j >1
est formée de 1 au dessus de la diagonale principale tandis que ses autre
termes sont nuls.
En développant det(A) suivant la
derniÃre ligne, dont seul le premier coefficient an est non nul, on obtient det(A)=(-1)n+1andet(T) avec pour T une matrice triangulaire supérieure
dordre n-1 dont tous les
coefficients diagonaux sont égaux à 1.
En conclusion : det(M)=(-1)n+1an.(an-an-1).(an-1-an-2)
(a2-a1)=![]()
_ Si w appartient au sous-espace
engendré par S, on pourra donc
lécrire comme combinaison linéaire w=a v akvk. Il sensuit par linéarité que
pour tout indice i >k
on aura q(w)+pi(w)=a (q+pi)(v1)+
..+ak(q+pi)(vk)
, doà lon déduit que Di est nul en tant que déterminant
dun systÃme lié.
_ Réciproquement, supposons chacun des n-k
déterminants Di nuls.
Pour un indice i >k donné, le vecteur (q+pi)(w) est donc combinaison linéaire du systÃme
Si=(
(q+pi)(v1),
,(q+pk)(vk)
).
En effet, limage par q de ce
systÃme, soit (q(v1),
.,q(vk)) est
libre par hypothÃse. Il sensuit que Si
est nécessairement libre. Or la matrice représentant Si dans Bi
est formée des k premiÃres
colonnes de la matrice de déterminant Di. Cette matrice dordre k+1 de déterminant nul et dont les k premiÃres colonnes forment un
systÃme libre est donc de rang k
et sa derniÃre colonne sera combinaison des k premiÃres. On peut
donc écrire légalité :
(1) ![]() .
.
En appliquant lendomorphisme q
à cette égalité on en déduit la relation (2) :
(2) ![]() car q
car q![]() pi=0 et q
pi=0 et q![]() q=q
q=q
Ainsi le coefficient ![]() ne dépend pas de
lindice i car il nest autre que la
composante aj sur q(vj) de q(w) dans la base (q(v1),
.,q(vk)
). En revenant à légalité (1) on en déduit alors par différence, la
relation pi(w)=a pi(v1)+
+akpi(vk)
ne dépend pas de
lindice i car il nest autre que la
composante aj sur q(vj) de q(w) dans la base (q(v1),
.,q(vk)
). En revenant à légalité (1) on en déduit alors par différence, la
relation pi(w)=a pi(v1)+
+akpi(vk)
Enfin, en additionnant (2) avec les n-k
égalités précédentes pour i variant
de k+1 à n on obtient finalement w=a v akvk qui assure lappartenance de w au sous-espace engendré par S.
Démonstration
par récurrence sur n.
_ Pour n=2 résultat évident : 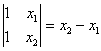
_ Supposons la propriété vraie pour un entier n ³2
et examinons un déterminant de Vandermonde Dn+1
dordre n+1.
Transformons dabord chacune des n
premiÃres lignes Li
en Li -Ln+1.
La premiÃre colonne voit alors tous ses termes nuls sauf le dernier égal
à 1.
En développant suivant cette colonne on obtient donc Dn+1=(-1)n+2det(An) avec An carrée dordre n
dont le terme générique est a(i,
j)=(xi)j-(xn+1)j.
En utilisant la linéarité suivant chaque ligne on peut alors sortir du
déterminant de An chacune
des différences xn+1-xi .
Ceci conduit à ![]() , avec pour coefficient générique de Bn :
, avec pour coefficient générique de Bn :
b(i, j)=![]()
Effectuons alors la séquence de remplacement : ![]() , pour j variant en
décroissant de n à 2. Le terme
générique de la ligne i pour j ³2 devient alors :
, pour j variant en
décroissant de n à 2. Le terme
générique de la ligne i pour j ³2 devient alors :
![]()
La premiÃre colonne de Bn
ne comportant que des 1, det(Bn)
est donc un déterminant de Vandermonde dordre n relatif à la suite dindéterminées x1,
.,xn.
Par hypothÃse de récurrence on peut donc écrire det(Bn)=![]() , et par suite :
, et par suite :
Dn+1=![]() , ce qui justifie lextension de la formule de calcul
à lordre n+1.
, ce qui justifie lextension de la formule de calcul
à lordre n+1.
a) Démonstration facile par récurrence sur n.
_ Pour n=2 D(x)=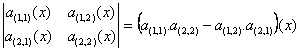 définit évidemment une fonction continue sur lintervalle I
daprÃs les théorÃmes sur la somme et le produit de fonctions
continues sur un intervalle.
définit évidemment une fonction continue sur lintervalle I
daprÃs les théorÃmes sur la somme et le produit de fonctions
continues sur un intervalle.
_ Supposons la propriété vraie pour un entier n ³2
et examinons un déterminant fonctionnel D(x)=det(A(x)) dordre n+1. En le développant suivant la
premiÃre colonne on obtient la formule classique : D(x)=![]()
Ai(x) désignant la matrice dordre n
obtenue à partir de A(x) en supprimant la premiÃre
colonne et la ligne dindice i.
DaprÃs lhypothÃse de récurrence, la fonction Di définie sur I par Di(x)=det(Ai(x)) est donc continue sur tout cet
intervalle et ceci pour tout i de
.
D est donc bien continue sur I comme
combinaison linéaire de produits de fonctions continues.
b) Ici aussi récurrence sur n.
_ Pour n=2 [a(1,1).a(2,2)-a(1,2).a(2,1)]=a(1,1).a(2,2)-a(1,2).a(2,1) +a(1,1).a(2,2)-a(1,2).a(2,1)
Ceci daprÃs les rÃgles de dérivation des produits et sommes de
fonctions dérivables.
On obtient bien la technique de dérivation annoncée.
_ Supposons la propriété vraie à lordre n et examinons avec les notations du a) un déterminant D(x)
fonctionnel dordre n+1. La formule
de développement employée plus haut montre que D est dérivable sur I suivant la formule :
D(x)=![]()
La premiÃre somme est le développement suivant la premiÃre
colonne du déterminant de la matrice obtenue en remplaçant la premiÃre
colonne de A(x) par celle des dérivées des fonctions composantes la constituant.
Etudions la deuxiÃme somme.
DaprÃs lhypothÃse de récurrence on peut écrire pour chaque i de :
![]() avec pour A(i, j)(x) la matrice obtenue en remplaçant la
colonne dordre j de Ai(x) par celle des dérivées, cest à dire la matrice obtenue en supprimant la
premiÃre colonne et la ligne dordre i
de la matrice Bj+1(x) déduite de A(x) en remplaçant la
colonne dordre j+1 par celle des
dérivées des composantes.
avec pour A(i, j)(x) la matrice obtenue en remplaçant la
colonne dordre j de Ai(x) par celle des dérivées, cest à dire la matrice obtenue en supprimant la
premiÃre colonne et la ligne dordre i
de la matrice Bj+1(x) déduite de A(x) en remplaçant la
colonne dordre j+1 par celle des
dérivées des composantes.
Par permutation des indices la deuxiÃme somme sécrit :
![]()
On a donc bien D(x)=![]() conformément à la formule attendue pour le rang n+1. Ceci achÃve la preuve par
récurrence.
conformément à la formule attendue pour le rang n+1. Ceci achÃve la preuve par
récurrence.
a)
Démonstration par récurrence sur n.
On notera o(i, j)(h) le terme générique de la matrice O(h)
et a(i, j) celui de A.
_ Pour n=1 et n=2 les vérifications sont évidentes.
_ Supposons la propriété vraie à lordre n et examinons la situation à lordre suivant.
En développant suivant la premiÃre colonne on a, toujours avec les
notations classiques :
det(A+O(h))=![]()
Or O(i,1)(h) est la matrice
carrée dordre n obtenue à
partir de O(h) en supprimant la premiÃre colonne et la ligne dindice i. Ses coefficients sont donc tous
négligeables devant h en 0 et
lhypothÃse de récurrence permet alors décrire det(A(i,1)+O(i,1)(h))=det(A(i,1))+o(h).
On en déduit alors le développement :
![]() On obtient bien pour h
voisin de 0 : det(A+O(h))=det(A)+o(h) ce qui conclut la récurrence.
On obtient bien pour h
voisin de 0 : det(A+O(h))=det(A)+o(h) ce qui conclut la récurrence.
b) DaprÃs létude précédente on peut déjà écrire le
développement au voisinage de 0 :
det(In+hA+O(h))=det(In+hA)+o(h).
On peut alors montrer facilement par récurrence sur n la relation : det(In+hA)=1+trace(A).h+o(h). Ici aussi les
vérifications initiales sont triviales et lhérédité se montre encore en
développant suivant la premiÃre colonne. det(In+1+hA)=[1+ha(1,1)][1+trace(A(1,1))h+o(h)]+![]()
En effet la matrice obtenue en éliminant de In+1+hA
la premiÃre ligne et la premiÃre colonne nest autre que In+hA(1,1) à laquelle on peut appliquer
lhypothÃse de récurrence.
Quand au déterminant obtenu en éliminant la premiÃre colonne et la ligne
dindice i >1, il peut sécrire, en développant suivant la premiÃre ligne, sous la
forme hDi(h) avec Di fonction continue de h.
En regroupant tous les termes négligeables devant h en 0 on obtient finalement : det(In+1+hA)=1+h[a(1,1)+trace(A(1,1)]+o(h)=1+htrace(A)+o(h).
En conclusion on a bien pour tout n :
det(In+hA+O(h))=1+h.trace(A)+o(h)
c) Si on note A(x)=![]() la matrice obtenue en remplaçant chacun des coefficients de
la matrice variable A par sa dérivée
au point x, on obtient trÃs
facilement le développement au voisinage de 0 : A(x+h)=A(x)+hA(x)+O(h).
la matrice obtenue en remplaçant chacun des coefficients de
la matrice variable A par sa dérivée
au point x, on obtient trÃs
facilement le développement au voisinage de 0 : A(x+h)=A(x)+hA(x)+O(h).
Si A(x) est supposée inversible on peut écrire A(x+h)=A(x).[In+hA-1(x).A(x)+O(h)]
On en déduit daprÃs la rÃgle du produit et létude précédente,
la relation :
det(A(x+h))=det(A(x)).[1+htrace(A-1(x).A(x))+o(h)]
Ceci nest autre quun développement dordre 1 de det(A(x+h)) au voisinage de h=0
On en déduit la formule de dérivation : ![]()
_
Examinons dabord le cas particulier c=0.
Le bloc inférieur gauche cA dordre n étant nul on a alors det( C )=det(aA).det(dA)=an.det(A).dn.det(A)=[det(A)]².[det(B)]n
_ Si c est non nul, transformons le
bloc inférieur droit dA en 0 grace
à la séquence de manipulations sur colonnes : ![]() , pour i variant de 1 à n.
, pour i variant de 1 à n.
Le bloc supérieur droit est changé dans cette opération en ![]()
Effectuons alors la suite déchanges ![]() pour i variant de 1 à n afin de se ramener au cas oà le
bloc inférieur gauche est nul. On en déduit :
pour i variant de 1 à n afin de se ramener au cas oà le
bloc inférieur gauche est nul. On en déduit :
det(C)=(-1)n![]()
On obtient bien det(C)=[det(A)]2.[det(B)]n.
a)
Soit k le plus petit entier tel que N k=0.(ordre de nilpotence de
N). Nous allons montrer par
récurrence sur k que N est toujours semblable à une
matrice triangulaire supérieure de diagonale principale nulle.
_ Si k=1 la vérification est évidente
puisque N=0.
_ Supposons la propriété vraie pour k
et examinons le cas dune matrice N
de Mn(K) dordre de nilpotence k+1. Notons f lendomorphisme de Kn représenté par N dans la base canonique.
Vu que f k+1=0
et f k ¹0 , la restriction g de f
à F=Im(f) est nilpotente
dordre k.
Par hypothÃse de récurrence il existe donc une base B de F telle que la matrice A
représentant g dans B=(u1,
.,
up) soit triangulaire supérieure de diagonale
principale nulle.
Complétons B en une base B de lespace total Kn. La matrice de f dans B est alors aussi du type demandé. En effet ses p premiÃres colonnes ne sont
autres que celles de A complétées par
des coefficients nuls, et limage par f
dun vecteur de B-B est combinaison
des vecteurs de B puisque ce systÃme est une base de Im(f).
La propriété étudiée se transmet donc bien du rang k au rang k+1.
b) DaprÃs ce qui précÃde, In+N sera semblable à une matrice
triangulaire supérieure dont tous les éléments de la diagonale principale
seront égaux à 1. On a donc par conservation du déterminant lors dun
changement de base : det(In+N)=1
c) Ecrivons A+N=A(In+A-1.N). On en déduit det(A+N)=det(A).det(In+M) avec M=A-1.N.
Par hypothÃse, N commute avec A et donc aussi avec A-1.
Puisque N est nilpotente dordre k on peut donc écrire la relation :
M k=(A-1)k.N k=0.
M est donc aussi nilpotente.
DaprÃs b) on peut donc écrire det(In+M)=1
, et par suite : det(A+N)=det(A).
Si
1, j, j² désignent les trois racines complexes de lunité, on déduit
immédiatement de légalité polynômiale X 3-1=(X-1)(X-j)(X-j²), la factorisation dans LK(E) suivante :
f 3-IE=(f-IE)(f-jIE)(f-j²IE).
Il suffit en effet dappliquer le morphisme classique de K-AlgÃbre reliant K[X] à LK(E) et transformant X en f.
fi
3-IE nétant pas injectif, son déterminant sera nul et on
en déduit daprÃs le théorÃme du produit que det(f-IE).det(f-jIE).det(f-j²IE)=0.
Un des trois facteurs est donc nécessairement nul, ce qui assure la non
injectivité de lendomorphisme f-aIE pour au moins un a de .
Effectuons
la séquence de manipulations sur les lignes :![]() pour i variant en
décroissant de n à 2. Vu la
relation fondamentale de construction du triangle de Pascal, le coefficient
dindice j de la ligne i devient :
pour i variant en
décroissant de n à 2. Vu la
relation fondamentale de construction du triangle de Pascal, le coefficient
dindice j de la ligne i devient :
_ 1-1=0 si j=1.
_ ![]() si 2 £j £i
si 2 £j £i
_ ![]() si j=i+1.
si j=i+1.
_ 0 si j >i+1.
En développant alors ce déterminant suivant la premiÃre ligne on obtient
la relation :
det(Tn)=det(Tn-1). On termine
en calculant det(T2)=![]()
Ainsi
n ³2 : det(Tn)=1.
En
utilisant la linéarité par rapport à la derniÃre colonne on peut
dabord décomposer Dn en
la somme An+Bn
des deux déterminants obtenus en remplaçant respectivement la derniÃre
colonne de la matrice dorigine dune part par une colonne formée uniquement de
1 et dautre part par la colonne dont tous les termes sont nuls sauf le
dernier, égal à n.
_ En développant Bn suivant cette mÃme
derniÃre colonne, il vient : Bn=nDn-1.
_ En soustrayant à chaque ligne de An la derniÃre ligne du tableau, on obtient un
déterminant triangulaire inférieur dont les termes de la diagonale principale
sont les entiers 1, 2,, n-1, 1
On en déduit immédiatement An=(n-1)! et par suite la relation de
récurrence :
Dn=(n-1)!+nDn-1
valable pour tout n ³2.
Remarquons alors que cette relation peut sécrire aussi : ![]()
Par sommation, lindice variant entre 2 et n,
on en déduit légalité : ![]()
Or D1=2 . On en déduit la
formule : ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2243
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved