| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
LIMITES
1) GENERALITES
A)
Introduction.
Le cadre
détude de ce chapitre est celui des fonctions à valeurs réelles,
définies sur une partie quelconque de R.
En ne se bornant pas aux seules fonctions définies sur un intervalle ou une
réunion finie dintervalles on englobe donc les suites numériques réelles ,
fonctions particuliÃres définies sur un ensemble discret, le plus
souvent N ou une section de N.
Plus tard nous étendrons la théorie aux suites et fonctions à valeurs
complexes.
En langage approximatif , un problÃme dit de limite apparait pour
une fonction f lorsque le comportement des images f(x) nous interpelle pour des valeurs de
la variable x de plus en plus proche
dun réel donné a (étude au voisinage
dun point ), ou lorsquon sintéresse à des valeurs extrÃmes de
la variable (étude au voisinage de linfini).
Par exemple : comment évolue le
quotient ![]() pour x voisin de 0, ou la puissance (1+
pour x voisin de 0, ou la puissance (1+![]() )n
lorsque lentier n devient de plus en
plus grand ?
)n
lorsque lentier n devient de plus en
plus grand ?
Parmi tous les comportements possibles il en est dassez réguliers, obéissant
au schéma suivant :
Les images étudiées f(x)
pourront toujours Ãtre rendues aussi proches que lon veut dun nombre l
en prenant x suffisamment voisin du
point détude a.
On dira alors que f admet pour limite
l en a, ou que f(x) tend vers l lorsque x tend vers a.
On voit bien que cette définition est encore floue et quune des conditions
pour en faire une base de la théorie est de préciser les notions de proximité dont il est fait mention.
Parmi les nombreuses procédures possibles nous choisirons celle reposant sur la
notion ensembliste de voisinage, permettant de traduire de façon concise et
rigoureuse les idées intuitives développées ci dessus.
B)
Notions de base et définitions élémentaires.
1) Compactifié de R
Pour unifier dans un seul énoncé les concepts de limites sans distinguer les
cas purement réels des comportements extrÃmes, il est commode dadjoindre
à R deux symboles appelés points
à linfini, notés +¥ et -¥.
La réunion ![]() =R est appelée compactifié de R.
=R est appelée compactifié de R.
_ Si on perçoit R comme une droite géométrique
graduée, ces nombres correspondent à des points fictifs aux deux
horizons opposées de cette droite.
_ On peut aussi saider de la bijection naturelle f entre ]-![]() ,
, ![]() [ et R définie par la tangente : x a f(x)=tan(x). Compactifier R revient à prolonger f aux bornes de son
intervalle de définition. (+¥ correspond alors à limage de
[ et R définie par la tangente : x a f(x)=tan(x). Compactifier R revient à prolonger f aux bornes de son
intervalle de définition. (+¥ correspond alors à limage de ![]() et -¥ à celle de -
et -¥ à celle de -![]() .)
.)
Le prolongement ![]() ainsi bati relie
bijectivement lintervalle fermé borné [-
ainsi bati relie
bijectivement lintervalle fermé borné [-![]() ,
,![]() ] au compactifié
] au compactifié ![]() .
.
On peut également prolonger la relation dordre usuelle sur R en posant :
x I![]() ¥ £ x £ ¥
¥ £ x £ ¥
Ceci permet entre autre daccepter -¥ et +¥ comme bornes dintervalles
fermés.
Ainsi ![]() =[-¥ ¥].
=[-¥ ¥].
2) Voisinages fondamentaux.
Définitions. On appelle voisinage fondamental :
_ Dun réel a, tout intervalle du
type ]a-a, a+a[
avec a réel strictement positif.
_ De +¥,
tout intervalle du type ]M,+¥]=]M,+¥ avec M réel.
_ De -¥,
tout intervalle du type [-¥,M[= ¥,M[ avec M réel.
Ceci permet déjà de préciser la notion dite de localité :
Effectuer une étude locale en un point a
de ![]() signifie se placer sur un voisinage de a. On parle aussi étude au voisinage du
point a.
signifie se placer sur un voisinage de a. On parle aussi étude au voisinage du
point a.
On dira par exemple que la fonction f
vérifie localement une propriété P au voisinage de a si et seulement si il existe un
voisinage V de a tel que la
restriction de f à V vérifie P.
Ainsi la
fonction partie entiÃre est localement constante au voisinage de chaque
élément de
R Z , mais pas au voisinage dun relatif , ni au voisinage
de +¥ et -¥.
La fonction cosinus est strictement positive au voisinage de 0, mais pas au
voisinage de ![]() , ni au voisinage de + ¥ ou - ¥.
, ni au voisinage de + ¥ ou - ¥.
La fonction ln est localement bornée au
voisinage de tout réel strictement positif, mais pas au voisinage de 0 ni au
voisinage de +¥.
Remarquons enfin, et cela sera particuliÃrement utilisé dans les
démonstrations à venir, que lintersection de deux voisinages
fondamentaux de a (plus généralement
dun nombre fini de ces voisinages) est encore un voisinage fondamental de a.
On notera V (a) lensemble de tous les voisinages fondamentaux de a.
On dira souvent voisinage en abréviation de voisinage fondamental.
3) Point adhérent.
On dit que le point a de ![]() est adhérent au sous ensemble I de
est adhérent au sous ensemble I de ![]() si et seulement si tout voisinage fondamental
de a rencontre I, cest à dire
a une intersection non vide avec I.
si et seulement si tout voisinage fondamental
de a rencontre I, cest à dire
a une intersection non vide avec I.
Il sagit donc dune notion un peu plus tiÃde que la relation
dappartenance au sens strict.
En langage simplifié un point adhérent à un ensemble est un point que
lon ne peut détacher de lensemble en question, qui est collé à
lensemble sans nécessairement y appartenir, de mÃme quun individu peut
adhérer pleinement aux idées dun parti politique sans aller jusquà en
prendre la carte. On note ![]() lensemble des points
adhérents à I. La définition sécrit alors :
lensemble des points
adhérents à I. La définition sécrit alors :
aI![]() V IV (a) V I ¹ Æ
V IV (a) V I ¹ Æ
_ Remarquons que le compactifié ![]() nest autre que ladhérence de R au sens de la définition précédente, ce
qui assure la cohérence des notations posées.
nest autre que ladhérence de R au sens de la définition précédente, ce
qui assure la cohérence des notations posées.
_ Ladhérence de ]1,3] est [1,3], ladhérence de R- est ![]() ,
ladhérence de [2,4] est [2,4]
,
ladhérence de [2,4] est [2,4]
La notion
dadhérence permet de préciser les points oà un problÃme détude
de limite est envisageable. En effet, selon la définition, si un élément a nadhÃre pas à
lensemble de définition I dune fonction f,
on pourra lisoler de cet ensemble, cest à dire trouver un voisinage V
de a ayant une intersection vide avec
I. Ainsi, localement, f ne sera pas
définie au voisinage de ce point a et
une étude de f au voisinage de a na donc aucune raison dÃtre.
Tout est maintenant en place pour donner la définition générale de limite.
4) Limite dune fonction numérique en
un point a.
Soit f une fonction définie sur le
sous-ensemble I de R, à valeurs réelles.
Considérons un élément a de ![]() adhérent à lensemble de définition I
de f et un nombre l du compactifié
adhérent à lensemble de définition I
de f et un nombre l du compactifié ![]()
On dit que f admet pour limite l au point a si et seulement si pour tout voisinage V de l il est toujours possible de trouver un voisinage W de a pour lequel f(I W)ÌV
![]()
![]()
Notations. On écrit alors pour
résumer : ![]() ou bien
ou bien ![]() et on dit également
que f(x)
tend vers l lorsque x tend vers a.
et on dit également
que f(x)
tend vers l lorsque x tend vers a.
Analysons le schéma de la définition. Il exprime bien de façon claire cette
fois lidée initiale :
Les images f(x)
pourront toujours Ãtre rendues suffisamment proche de l , cest à dire entrer dans un
voisinage V donné de l à condition
dagir en finesse sur x , cest
à dire de placer cette variable dans un voisinage convenable W du point
détude.
_ Dans ce canevas, V est la contrainte de proximité imposée. Le but est
dobtenir f(x)IV.
_ Pour le réaliser, on cherche une zone suffisante autour de a, cest à dire un voisinage W de
ce point de façon que lon ait bien : xII W Þ f(x)IV .
Il va de soit que W nest pas universel, mais dépend au contraire du voisinage
V imposé.
Il sagit dune course à la précision, à chaque contrainte de
proximité sur les images on essaie de répondre de façon positive en
sapprochant suffisamment prÃs de a,
on cherche une zone de sécurité W réalisant la condition imposée.
Pour assimiler la définition, le lecteur pourra sentrainer à transcrire
celle ci dans des cas particuliers.
_ Ainsi pour établir que lim1
f(x)=3, il faut montrer que quel
que soit le réel e
strictement positif donné, on peut toujours trouver un réel a>0 tel que (xII et![]()
_ Pour montrer que lim2 f(x)=-¥, il faudra prouver que pour tout
réel M donné, on peut toujours trouver un réel a>0 tel que : ![]()
_ Pour prouver que la suite n a
f(n) tend vers 5 lorsque n tend vers +¥ , il faudra montrer que pour
tout réel e >0 donné, on peut toujours trouver
un rang n0 tel que :
nIN n ³n Þ![]()
5) Unicité de la limite.
On verra plus loin quune fonction nadmet pas toujours une limite en un point a adhérent à son ensemble de
définition I. Par contre on va montrer immédiatement que f ne peut admettre deux limites distinctes en un mÃme point.
La preuve est simple et repose sur la remarque suivante : si l1 et l2 désignent deux éléments distincts de ![]() ,
il est trÃs facile de les séparer , cest à dire de trouver
deux voisinages respectifs V1 et V2 de chacun de ces
points dont lintersection est vide.
,
il est trÃs facile de les séparer , cest à dire de trouver
deux voisinages respectifs V1 et V2 de chacun de ces
points dont lintersection est vide.
Si f admettait à la fois pour
limite l1 et l2 au point a on pourrait donc, conformément
à la définition, trouver un voisinage W1 de a tel que f(I W1)ÌV1 et un voisinage W2
de ce mÃme point a pour lequel f(I W2 )ÌV2. Considérons alors
lintersection W=W1 W2.
Cest encore un voisinage fondamental de a
et par suite a une intersection non vide avec I puisque a adhÃre à cet ensemble de définition I. Par suite
limage par f de W I est non vide, ce qui est
contradictoire avec le choix de V1 et V2 à cause
de f(I W)ÌV1 V2=Æ.
6) Variantes de la définition
générale.
a Limite à droite dun réel
a :
Sobtient en restreignant lensemble détude de la fonction aux valeurs
strictement supérieures à a.
Notations : ![]()
a Limite à gauche dun réel
a : MÃme principe, mais en
restreignant létude aux nombres strictement inférieures à a. Notations similaire : ![]()
a Limite réelle par valeurs
supérieures.
Si lima f(x)=l avec l
réel et si il existe un voisinage W de a
tel que : xII W Þ
f(x) >l , on dira que f tend vers l par valeurs supérieures et on écrira pour résumer ceci : lima f =l+
a Limite réelle par valeurs inférieures.
Schéma analogue avec cette fois f de valeurs strictement inférieures
à l au voisinage de l.
notation résumé : lima
f =l-
C) Transformations pratiques fondamentales.
Remarquons pour commencer quun voisinage fondamental quelconque ]a-a,a+a[ dun réel donné a nest autre que limage du voisinage
]-a a[ de 0 par la translation h at(h)=h+a.
Selon le schéma de définition mÃme, dire que f admet pour limite l en a revient alors à dire que la
composée g=f![]() t admet pour limite l
en 0, la fonction g étant définie sur
limage réciproque J=t-1(I) de lensemble de définition I de f.
t admet pour limite l
en 0, la fonction g étant définie sur
limage réciproque J=t-1(I) de lensemble de définition I de f.
En effet on vérifie immédiatement que 0 adhÃre bien à J puisque I ]a-a,a+a[=t(J a a[)
Tout voisinage de 0 rencontre donc J si et seulement si tout voisinage de a rencontre I.
Ainsi toute étude de limite en un réel a
pourra se ramener à une étude de limite en 0 grace au changement de
variable x=a+h
![]()
Dans le mÃme esprit, notons que pour tout réel M>0 linégalité x >M équivaut à 0<![]()
Létude dune limite éventuelle au voisinage de +¥ peut donc se ramener à
létude dune limite à droite en 0 grace au changement de variable ![]() . Plus précisément on montre facilement léquivalence
suivante, en revenant aux schémas de définition :
. Plus précisément on montre facilement léquivalence
suivante, en revenant aux schémas de définition :
![]()
Lensemble de définition J de la nouvelle fonction h ag(h)=![]() est bien sÃr défini ici par
est bien sÃr défini ici par
J=.
Enfin, pour renvoyer une étude au voisinage de -¥ à une étude au voisinage
de 0, il suffira de poser ![]() avec la contrainte h >0. On montre aussi sans problÃmes
léquivalence suivante
avec la contrainte h >0. On montre aussi sans problÃmes
léquivalence suivante
![]()
Les changements de variable précédents peuvent Ãtre utilisés aussi au
niveau des images.
Par exemple, obtenir une image f(x) appartenant au voisinage ]l-e, l+e[ du réel l revient à faire entrer la différence f(x)-l dans le voisinage ]-e e[ de 0.
Doà léquivalence immédiate, toujours par examen des schémas de
définition :
limx
aa
f(x)=l
limx aa
f(x)-l=0
.
On vérifie tout aussi facilement :
![]() et
et ![]()
Tout problÃme détude de limite pourra donc toujours se ramener, par un
emploi convenable des changements de variable décrits ci dessus, à une
schéma standard de fonction de limite nulle en 0.
_ Ainsi : ![]()
_ ![]()
Schéma classique de majoration pour les fonctions de limite nulle en 0.
Nous verrons par la suite que pour la plupart des fonctions usuelles, on peut
établir que
lim0 g(h)=0 en mettant en évidence au voisinage
du point détude 0 une majoration du type ![]() avec K et m
réels strictement positifs. Pour un réel e strictement positif donné, il suffit en
effet de prendre
avec K et m
réels strictement positifs. Pour un réel e strictement positif donné, il suffit en
effet de prendre 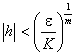 pour réaliser la
contrainte imposée :
pour réaliser la
contrainte imposée : ![]() .
.
Plus généralement, si on dispose au voisinage de 0 dune majoration du type ![]()
avec u de limite nulle en 0, la
fonction g aura aussi pour limite 0
à lorigine.
En effet, pour réaliser ![]() pour un e donné, il suffira de rendre
pour un e donné, il suffira de rendre ![]() strictement inférieur
à e, ce
qui sera toujours possible vu lhypothÃse sur u.
strictement inférieur
à e, ce
qui sera toujours possible vu lhypothÃse sur u.
D)
Limite dune restriction.
ThéorÃme : Si la fonction f définie sur lensemble I admet une limite l au point a, toute restriction g de f à un sous-ensemble J de I tel que a adhÃre encore à J admet aussi pour limite l en ce mÃme point a.
Preuve. Soit V
un voisinage donné de l. Par
hypothÃse sur f on peut
trouver un voisinage W de a tel que f(I W)ÌV.
J étant inclus dans I on en déduit immédiatement f(J W)ÌV, cest à dire g(J W)ÌV.
g a donc bien aussi pour limite l au point a.
Ce résultat de démonstration particuliÃrement simple peut servir de base
pour établir par labsurde une preuve de non existence de limite en un point.
Supposons en effet que lon puisse trouver pour une mÃme fonction f deux restrictions g1 et g2
à des sous ensembles respectifs J1 et J2 de I
telles que lima g1
¹lima g2.
Une telle fonction ne peut donc avoir de limite l au point a, car
daprÃs le théorÃme ci-dessus et le principe dunicité de la
limite on aurait dans ce cas : lima
g1 =l=lima g2.
Par exemple, pour établir que la fonction sinus nadmet pas de limite au
voisinage de +¥,
il suffit de considérer dune part sa restriction g1 à lensemble J1= auquel +¥ adhÃre et pour laquelle de maniÃre évidente ![]() , et dautre part la restriction g2 à la partie J2= admettant pour limite 1 en +¥.
, et dautre part la restriction g2 à la partie J2= admettant pour limite 1 en +¥.
La réciproque du théorÃme précédent est fausse. Il suffit de
reconsidérer lexemple ci dessus pour sen persuader. La fonction sinus nadmet
pas de limite en +¥,
pourtant sa restriction à lensemble des multiples de p auquel +¥ adhÃre est identiquement
nulle donc admet pour limite 0 en +¥.
Par contre, si on parvient à montrer que la restriction g de f
à un sous ensemble du type J=I W0 , avec pour W0
un voisinage fondamental de a, admet
une limite l au point a, on pourra conclure que f admet également pour limite l en a.
En effet, soit V un voisinage imposé de l.
Par hypothÃse sur g il existe
un voisinage W de a pour lequel g(W J)ÌV. Or W J=W I W0 .
Il suffit alors de remarquer queW1=W W0 est encore un
voisinage fondamental de a, en tant
quintersection de deux voisinages de a,
et que g(W J)= f(W1 I)
On a donc bien réalisé la contrainte f(x)IV en plaçant x dans un bon voisinage de a.
Ceci étant réalisable pour tout V on a bien prouvé lima f=l.
Ce résultat est appelé le principe de
localité de létude dune limite. On peut lénoncer ainsi :
Dans toute étude de limite dune fonction f en un point a, il est toujours permis de restreindre lensemble de définition I de f à sa trace I U sur un voisinage fondamental U de a.
Nous noterons également le résultat suivant demploi fréquent, surtout pour
létude des suites numériques et que nous appellerons principe de recouvrement :
Si Lensemble de définition I de f est égal à la réunion J1 J2 et que chacune des restrictions g1 et g2 de f aux sous ensembles respectifs J1 et J2 admet pour limite l au point a, alors f admet également pour limite l au point a.
Preuve. Soit V un voisinage donné de l.
Par hypothÃse sur g1
et g2 il existe deux
voisinages respectifs de a soient W1
et W2 , tels que g1(J1 W1)ÌV et g2(J2 W2)ÌV.
Considérons alors le voisinage fondamental W=W1 W2.
I étant réunion de J1 avec J2 (recouvrement), on a donc
de maniÃre évidente :
f(W I)Ì
g (J1 W1) g (J2 W2)ÌV, ce qui achÃve la
démonstration.
2)
TECHNIQUES USUELLES DE CALCUL DES LIMITES.
A)
RÃgles opératoires
Soient deux
fonctions numériques f et g que lon a étudié au voisinage dun
élément a et pour lesquelles on a mis
en évidence de limites respectives l
et m en ce point. En rÃgle
générale, la seule connaissance des valeurs l
et m suffit pour en déduire le
comportement limite de la somme, de la différence, du produit, du quotient de
ces deux fonctions au voisinage de ce mÃme point a.
Les résultats essentiels sont consignés de maniÃre abrégée dans les
tableaux suivants oà par convention les lettres l et m désignerons
uniquement des valeurs réelles de
limites. Les limites infinies seront notées en clair par les symboles +¥ ou -¥.
On notera des zones dombre correspondant aux cas dexception dits
dindétermination et pour lesquels une étude plus fine du rapport de force
entre f et g est nécessaire au voisinage du point détude. Cette impossibilité
de conclure à laide dune rÃgle générale sera représentée par un
point dinterrogation ?.
Sommes.
|
lima f |
l |
l |
l |
¥ |
¥ |
¥ |
|
lima g |
m |
¥ |
¥ |
¥ |
¥ |
¥ |
|
lima (f+g) |
l+m |
¥ |
¥ |
¥ |
¥ |
Opposé.
|
lima f |
l |
¥ |
¥ | ||
|
lima -f |
-l |
¥ |
¥ |
Produits.
|
lima f |
l |
l¹ |
l ¹ |
¥ |
¥ |
¥ | |
|
lima g |
m |
¥ |
¥ |
¥ |
¥ |
¥ |
|
|
lima (f.g) |
l.m |
¥ si l> ¥ si l< |
¥ si l> ¥ si l< |
¥ |
¥ |
¥ |
Inverse.
|
lima f |
l¹ |
¥ |
¥ |
||
|
lima ( |
|
¥ |
¥ |
Différences, quotients.
On utilisera les tableaux ci-dessus et les décompositions
suivantes :
f -g=(f)+(-g) ; ![]()
On aura donc une indétermination pour la différence lorsque les deux fonctions
ont des limites infinies de mÃme signe et pour le quotient lorsque
numérateur et dénominateur tendent simultanément vers 0 ou ont chacun une
limite infinie.
Preuves.
La grande majorité des résultats précédents sobtiennent de maniÃre
pratiquement évidente en examinant le schéma de la définition générale de
limite. Cest par exemple le cas pour les rÃgles concernant les opposés
et les inverse.
Nous naborderons donc que les démonstrations moins évidentes, laissant au
lecteur le soin de rédiger les preuves plus élémentaires, excellent exercice
pour assimiler la définition de base.
Les fonctions abordées seront supposées définies sur un mÃme ensemble I
auquel a adhÃre.
a) Cas dune somme de deux fonctions de limite réelle.
On est ici dans une situation du type f(x)=l+u(x)
et g(x)=m+v(x) avec lima u=lima
v=0
On en déduit (f+g)(x)=l+m+(u+v)(x)
.
Vérifier que f+g tend vers l+m au point a revient donc à prouver que la somme de deux fonctions de
limite nulle en a, soient u et v,
est encore de limite nulle en ce point.
Pour ceci considérons linégalité triangulaire ![]()
Elle montre que pour réaliser une contrainte du type ![]() avec e réel strictement positif imposé,
il suffit dassurer simultanément
avec e réel strictement positif imposé,
il suffit dassurer simultanément ![]() .
.
Or la premiÃre inégalité peut sobtenir en plaçant x dans un certain voisinage W1 de a, ceci puisque u tend
vers 0 au point a. De mÃme
puisque v a pour limite 0 en ce
point, on pourra trouver un voisinage W2 de a tel que sur I W2 on ait ![]()
Il est maintenant clair que sur I W avec W=W1 W2 on a bien les deux
majorations espérées. On a bien trouvé un voisinage W de a tel que xII W Þ ![]() .
.
b) Somme dune fonction f de
limite réelle l avec une fonction g tendant vers +¥
Pour vérifier que (f+g) tend vers +¥ au point a nous faut montrer que lon pourra réaliser une contrainte
quelconque du type f(x)+g(x)
>M en plaçant x dans un voisinage convenable de a.
Utilisons dabord le fait que f
admette pour limite l en a.
]l-1, l+1[ étant un voisinage particulier de la limite, on peut
déjà trouver un voisinage W1 de a tel que : xII W1 Þ f(x)I ]l-1, l+1[
Sur I W1 on a donc la
minoration : (f+g)(x)>g(x)+l-1.
Pour réaliser la minoration f(x)+g(x) >M, il suffit donc darriver
à g(x)>M-l+1.
Or une telle minoration est toujours possible en restreignant x à un voisinage adéquat W2
de a, ceci vu
lhypothÃse : g tend vers
+¥ en a.
Si on considÃre le voisinage W=W1 W2, on a bien
limplication : xIW I Þ f(x)+g(x) >M
c) Produit de deux fonctions de limites réelles.
Utilisons les notations de la situation précédente a). On en déduit pour le
produit :
(f.g)(x)=l.m+l.v(x)+m.u(x)+u(x)v(x).
Pour montrer que ce produit tend vers l.m
en a, il nous faut donc montrer que
la somme
l.v+m.u+u.v a pour limite 0 en a.
Pour cela remarquons dabord que daprÃs linégalité triangulaire, on a
la majoration évidente : ![]() avec pour K un réel choisi strictement supérieur
à 1 et aux valeurs absolues de l et m.
avec pour K un réel choisi strictement supérieur
à 1 et aux valeurs absolues de l et m.
Soit alors e un
réel strictement positif donné.
_ Puisque u a pour limite 0 en a, il est possible de réaliser ![]() en plaçant x sur un voisinage convenable W1
de a.
en plaçant x sur un voisinage convenable W1
de a.
_ De mÃme, puisque v tend vers
0 en a il est possible de rendre la
valeur absolue de v(x) strictement inférieure à 1 et
à ![]() en restreignant x à
un voisinage W2 de a.
en restreignant x à
un voisinage W2 de a.
Pour xIW1 W2 I on obtient donc bien : ![]()
d) Inverse dune fonction f de
limite réelle l non nulle.
Toujours suivant les notations de a) nous pouvons écrire :
![]()
Puisque u tend vers 0 au point a et que l est non nul, il est toujours possible de trouver un voisinage W1
de a pour lequel ![]() .
.
On en déduit alors ![]()
Sur un tel voisinage W1 on a donc la majoration : 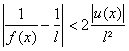
Si on nous impose une contrainte du type 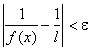 , il suffira donc de
se placer dabord sur W1 , puis de réaliser
, il suffira donc de
se placer dabord sur W1 , puis de réaliser ![]() .
.
Or cette derniÃre majoration peut devenir effective en restreignant x à un voisinage W2 de
a, ceci puisque u admet 0 pour limite en a.
En conclusion, xIW1 W2 I Þ 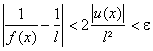
Linverse de f tend bien vers
linverse du nombre l au point détude a.
B)
ThéorÃme de composition.
Considérons un schéma de composition classique mettant en jeu deux fonctions
numériques :
![]()
Soit t0 un point adhérent
à I et x0 adhérent
à J.
![]()
La preuve sobtient de maniÃre élémentaire en revenant à la
définition initiale.
Soit en effet un voisinage fondamental donné V de l.
_ Puisque f tend vers l en x0,
il existe un voisinage U de x0
tel que f(U J)Ì V
_ Comme j
tend vers x0 en t0 , on pourra trouver un
voisinage W de t0 tel que j(W I)ÌU.
j étant à valeurs dans J,
on peut donc écrire j(W I)ÌU J et par suite f(j(W I))ÌV
On a donc bien obtenu un voisinage de t0
, soit W, dont limage par la composée f![]() j est
incluse dans le voisinage imposé V de l.
Ceci étant possible quelque soit V, on peut conclure suivant la définition
générale que f
j est
incluse dans le voisinage imposé V de l.
Ceci étant possible quelque soit V, on peut conclure suivant la définition
générale que f![]() j
tend vers l en t0.
j
tend vers l en t0.
Application à un constat de non existence de limite en un point.
Concernant cette situation on a vu précédemment une technique reposant sur
létude des restrictions. Le théorÃme de composition établi ci dessus
donne facilement une autre méthode pour établir la non existence dune limite
pour une fonction f en un point x0 adhérent à son ensemble de définition J.
On procÃde encore par labsurde. Supposons que f admette pour limite l
en x0
Pour toute suite n aan à valeurs dans J et telle
que limn a ¥
an=x0 on aura donc
nécessairement, grace au théorÃme de composition : ![]()
Il nous suffit donc, pour apporter une preuve dune impossibilité de limite en x0 , de trouver deux suites n aan et n abn , à valeurs dans J ,
tendant chacune vers x0
pour n tendant vers +¥ et telles que ![]()
C)
Limites des fonctions usuelles.
1) Polynômes et fractions rationnelles.
Examinons dabord les cas élémentaires des fonctions constantes et de
lidentité.
_ Il est clair quune fonction f
prenant en tout point de R la mÃme valeur C admet
pour limite cette constante C en tout point a
de ![]() .En
effet si V est un voisinage imposé de C, limage f(W) dun voisinage
quelconque de a sera bien contenu de
maniÃre triviale dans V puisque toute image coÃncide exactement
avec le point central C de V.
.En
effet si V est un voisinage imposé de C, limage f(W) dun voisinage
quelconque de a sera bien contenu de
maniÃre triviale dans V puisque toute image coÃncide exactement
avec le point central C de V.
On est dans une situation de stabilité
parfaite, les images stagnent sur la limite C.
_ Si f est la fonction identique sur R, on montre tout aussi facilement que f tend vers a en tout point a de ![]() .
En effet pour tout voisinage V donné de a,
limage par f de ce mÃme V
coÃncide parfaitement avec V. Lidentité clone chaque point et chaque
voisinage dun point donné. La réponse à une contrainte de proximité
donnée est exactement la redite de cette contrainte.
.
En effet pour tout voisinage V donné de a,
limage par f de ce mÃme V
coÃncide parfaitement avec V. Lidentité clone chaque point et chaque
voisinage dun point donné. La réponse à une contrainte de proximité
donnée est exactement la redite de cette contrainte.
Grace à ces deux premiers résultats et en utilisant les théorÃmes
sur les produits et sommes de fonctions ayant des limites, on en déduit alors
que pour un polynôme P quelconque, défini par P(X)=a0+a1X+
.+anXn, on aura en chaque réel x0 : ![]()
On exprime cette régularité en disant que le polynôme P est continu sur R
Plus généralement, on dira quune
fonction f est continue en un point x0
de son ensemble de définition si et seulement si ![]() . On dira quelle est continue sur lensemble I si et
seulement si elle est continue en tout point de I.
. On dira quelle est continue sur lensemble I si et
seulement si elle est continue en tout point de I.
En utilisant la rÃgle de limite dun quotient, on montre ensuite
facilement quune fonction rationnelle est continue en tout point de son
ensemble de définition.
En effet si x0 nest pas
racine du polynôme Q, on aura : ![]() .
.
Pour le comportement au voisinage de +¥ ou - ¥ il suffit pour P polynôme non constant deffectuer la
factorisation : 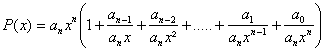 pour en déduire en
invoquant à nouveau les théorÃmes sur les sommes et produits
que :
pour en déduire en
invoquant à nouveau les théorÃmes sur les sommes et produits
que :
![]() .
.
On démontre également que la limite dune fraction rationnelle en une borne
infinie est égale à la limite en cette mÃme borne du quotient du
terme dominant de son numérateur par le terme dominant du dénominateur.
2) Racines n-iÃmes.
_ Pour tout entier n au moins égal
à 2, on connait la formule de factorisation :
an-bn=(a-b)(an-1+an-2b+
..+abn-2+bn-1)
Si a et b sont des réels positifs, on en déduit en particulier : ![]()
Appliqué à ![]() avec x et x0 réels strictement positifs, on en
déduit la majoration :
avec x et x0 réels strictement positifs, on en
déduit la majoration : 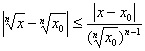
On en conclÃt que lécart entre ![]() peut Ãtre rendu
plus petit que tout e
positif donné en réalisant
peut Ãtre rendu
plus petit que tout e
positif donné en réalisant ![]() . Ainsi
. Ainsi ![]() et ceci pour tout x0 >0.
et ceci pour tout x0 >0.
_ Pour létude en 0 on utilise simplement léquivalence : ![]()
La fonction racine dordre n a donc
pour limite 0 en 0 ce qui assure avec létude précédente la continuité de cette
fonction en tout point de [0,+¥[
_ Enfin, pour létude au voisinage de +¥ remarquons que pour tout M réel positif :
![]() . On en déduit lim+¥
. On en déduit lim+¥ ![]() =+¥
=+¥
3) Fonctions trigonométriques.
Nous admettrons comme base de létude suivante lencadrement : sin(h)
£h £tan(h) .
supposé valable pour tout h de [0,![]() [.
[.
On peut sen convaincre de maniÃre géométrique en examinant le cercle
trigonométrique unité de centre O et en comparant laire dun secteur
élémentaire ![]() =(OAM) mesuré par h
en radians avec les aires des triangles rectangles (OHM) et (OAT)
respectivement contenu et contenant ce secteur, avec pour H la projection
orthogonale de M sur laxe (OA) des
cosinus et T trace de la droite (OM) sur laxe des tangentes.
=(OAM) mesuré par h
en radians avec les aires des triangles rectangles (OHM) et (OAT)
respectivement contenu et contenant ce secteur, avec pour H la projection
orthogonale de M sur laxe (OA) des
cosinus et T trace de la droite (OM) sur laxe des tangentes.
Il apparait ![]() dont on déduit
facilement lencadrement en question. Pour une justification rigoureuse il est
indispensable de passer par une définition analytique précise des fonctions
trigonométriques de base sinus et tangente, mais ceci dépasse le cadre qui nous
est accordé.
dont on déduit
facilement lencadrement en question. Pour une justification rigoureuse il est
indispensable de passer par une définition analytique précise des fonctions
trigonométriques de base sinus et tangente, mais ceci dépasse le cadre qui nous
est accordé.
Ceci posé nous en déduirons dabord les limites essentielles suivantes :
|
|
|
|
|
_ Pour la premiÃre, remarquons dabord que lencadrement 0£sin(h)£h valable sur [0, ![]() [ entraine immédiatement :
[ entraine immédiatement : ![]() . Pour la limite à gauche, la fonction sinus étant
impaire, on pourra écrire grace au théorÃme de composition :
. Pour la limite à gauche, la fonction sinus étant
impaire, on pourra écrire grace au théorÃme de composition :
![]()
_ Pour la deuxiÃme, la formule de larc double nous donne cos(h)=1-2sin²(![]() ).
).
Or, toujours grace au théorÃme de composition : ![]() .
.
Enfin, daprÃs les théorÃmes sur les produits et sommes, on
conclÃt que lim0 cos(h)=1.
_ Remarquons que lencadrement initial peut sécrire également sous la forme :
Sur [0,![]() [ hcos(h) £sin(h) £
h. On en déduit que sur ]0,
[ hcos(h) £sin(h) £
h. On en déduit que sur ]0,![]() [ :
[ : ![]()
DaprÃs la majoration : ![]() et vu que lim0
cos(h)=1, on en déduit
aussitôt :
et vu que lim0
cos(h)=1, on en déduit
aussitôt :
![]()
Pour la limite à gauche on utilise à nouveau le caractÃre
impair du sinus : ![]()
_ Enfin si on revient à la formule de larc double pour le cosinus, 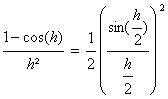
On en conclÃt daprÃs létude précédente et les théorÃmes
classiques : ![]()
_ Ces premiers résultats établis, on déduit facilement des formules daddition
la continuité de sinus et cosinus en tout réel a. Il suffit décrire, pour h
voisin de 0 :
sin(a+h)=sin(a)cos(h)+sin(h)cos(a) et cos(a+h)=cos(a)cos(h)-sin(a)sin(h) puis dutiliser
les rÃgles opératoires concernant les limites.
4) Fonctions logarithme, exponentielle et puissances généralisées.
Elles sont également continues en tout point de leur ensemble de définition.
Pour ce qui concerne les limites aux bornes et les croissances comparées, les
principaux résultats sont résumés dans le tableau suivant dans lequel a désigne un réel quelconque strictement
positif.:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Preuves.
Nous utiliserons ici aussi un encadrement de base portant sur la fonction
logarithme Népérien, que lon obtient facilement dans les diverses
constructions rigoureuses de cette fonction. (Nous en évoquerons deux dans les
chapitres à venir, lune sappuyant sur une convergence de suite de
fonctions, lautre sur la notion dintégrale)
_ Admettons donc provisoirement lencadrement ![]() pour tout x de [0,1]
pour tout x de [0,1]
Retenons simplement dabord : sur [0, 1] : 0 £ ln(1+x)
£ x.
On en déduit immédiatement ![]()
Pour létude de la limite à gauche utilisons les propriétés algébriques
fondamentales des logarithmes. Pour tout x
de [0,1[ :![]()
Ainsi ![]() daprÃs le
résultat précédent allié au théorÃme de composition.(
daprÃs le
résultat précédent allié au théorÃme de composition.( ![]() tend vers 0 par
valeurs supérieures à droite de 0)
tend vers 0 par
valeurs supérieures à droite de 0)
Pour tout x0 >0 on a alors : ![]() .
.
La fonction logarithme Népérien est donc continue sur tout ]0,+¥[.
_ En considérant les quotients par x>0, lencadrement initial se
traduit ![]() ,
,
puis ![]() , dont on
déduit :
, dont on
déduit : ![]() .
.
Pour létude à gauche de 0 on écrira comme précédemment :
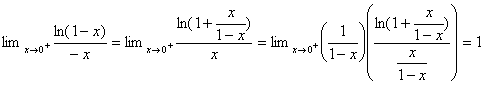
Ceci daprÃs la rÃgle du quotient, le théorÃme de
composition et la rÃgle du produit.
_ Pour vérifier que ln tend vers +¥ en +¥, remarquons que pour assurer une
contrainte du type ln(x)>M il suffit de prendre x
strictement supérieur à 2n,
lentier n étant choisi de façon que n ³![]() .
.
En effet, par croissance stricte de la fonction logarithme népérien et
propriétés algébriques, il vient : x>2n Þ ln(x)>ln(2n)=nln(2). Donc x >2n Þ ln(x)
>M
_ Grace au changement de variable x=![]() , on en déduit le comportement de ln au voisinage de
0 :
, on en déduit le comportement de ln au voisinage de
0 : ![]()
_ Pour la continuité de lexponentielle à lorigine, remarquons que pour
e réel de ]0, 1[ donné, la
contrainte exI e e[ sera réalisée si on prend x dans un voisinage de 0 inclus dans
lintervalle ]ln(1-e),
ln(1+e)[. (Ceci par croissance stricte
de lexponentielle, réciproque de ln)
_ Pour x0 réel quelconque
on a alors : ![]()
Lexponentielle est bien continue en tout point.
_ Pour M>0
donné, ex>M x>ln(M),
ce qui assure ![]()
_ ![]()
_ A partir de ![]() , grace au changement de variable x=et et la continuité de lexponentielle à
lorigine on en déduit :
, grace au changement de variable x=et et la continuité de lexponentielle à
lorigine on en déduit : ![]() et par suite :
et par suite : ![]()
_ Pour létude des fonctions puissances dexposant réel a quelconque, rappelons quelles sont définies sur ]0,+¥[ à partir du couple (ln,
exp) par la formule ![]()
Ainsi pour a>0 ,![]() et
et ![]()
![]()
_ Pour les comparaisons avec les fonctions suivantes nous admettrons que
linégalité de base :
ln(1+x) £x est valable sur ]0,+¥[.
On en déduit en particulier que pour tout x>1 et tout réel b : 0< ln(xb)< xb et que, par
conséquence : 0< bln(x)< xb.
Pour tout réel x>1 et tout couple de réels
strictement positifs (a, b) on peut donc écrire
lencadrement : ![]() dont on déduit :
dont on déduit : ![]() .
.
Il suffit pour cela de choisir pour a>0 donné un réel b tel que 0<b<a.
_ Grace au changement de variable h=![]() on déduit alors immédiatement :
on déduit alors immédiatement :
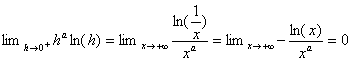
_ De mÃme en posant x=et,
![]() conduit grace au
théorÃme de composition, à :
conduit grace au
théorÃme de composition, à :
![]() , ou encore
à :
, ou encore
à : ![]() .
.
En passant à linverse puis en composant avec la fonction x a![]() ,
on obtient la formule :
,
on obtient la formule : 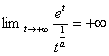 . Comme la fonction a
a
. Comme la fonction a
a![]() relie bijectivement ]0, +¥[ à lui mÃme, on
peut conclure que pour tout a
strictement positif :
relie bijectivement ]0, +¥[ à lui mÃme, on
peut conclure que pour tout a
strictement positif : ![]() .
.
D)
Résultats liés à la relation dordre sur R
ThéorÃme dencadrement.
Soient f, g, h, trois fonctions à valeurs
réelles définies sur le sous ensemble I de R auquel adhÃre x
0. Si au voisinage de x0
on a g(x)£ f(x)£ h(x) et si ![]()
on peut alors en déduire ![]()
La preuve est simple. Soit V un voisinage fondamental de x0. Les fonctions g
et h ayant pour limite l en x0,
on pourra trouver des voisinages respectifs W1 et W2 de
ce point tels que :
g(W1 I )ÌV et h(W2 I)ÌV.
LhypothÃse nous dit aussi quil existe un voisinage U de x0 tel que sur U I, g(x)£
f(x)£ h(x).
Remarquons que tout voisinage fondamental V, que ce soit dun réel ou de ![]() , possÃde la propriété de convexité, cest à
dire que si deux réels a et b appartiennent à V, le segment
dextrémités a et b est contenu intégralement dans V.
, possÃde la propriété de convexité, cest à
dire que si deux réels a et b appartiennent à V, le segment
dextrémités a et b est contenu intégralement dans V.
Si on considÃre le voisinage W=W1 W2 U de x0, il est maintenant clair daprÃs ce qui
précÃde, que : f(W I) ÌV.
Remarques. Si l est une limite
infinie, il nest pas nécessaire de disposer dun encadrement complet de f mais seulement de la minoration f(x) ³g(x) dans le cas oà ![]()
et de la majoration seule f(x) £h(x) si on sait que ![]()
Les preuves de ces variantes sont évidentes, il suffit dadapter la
démonstration ci-dessus.
ThéorÃmes de limite monotone.
Avant dénoncer ces résultats fondamentaux, rappelons et précisons certaines notions
fondamentales concernant la comparaison des réels.
Majorant dune partie J de R
On appelle ainsi tout réel M supérieur ou égal à chacun des éléments de
J.
On dit alors que J est majorée par M.
Borne supérieure dune partie majorée non vide J de R
Dans toute construction rigoureuse du corps ordonné des nombres réels on
établit que pour chaque partie non vide majoré J de R il existe un plus petit majorant de J appelé borne
supérieure de lensemble J et que nous noterons dans tout ce qui suit : sup(J).
Nous considérerons ici cette propriété dite de la borne supérieure comme un
axiome de base de lAnalyse sur R. Attention, il sagit dune
affirmation dexistence dun meilleur majorant de J, au sens dÃtre le
plus petit possible, mais nous ne disposons ici daucune technique pratique
pour le mettre en évidence.
Ainsi si on considÃre J=, il est clair que J est majorée
par 6, mais la valeur exacte de sup(J) nous échappe.
Minorant dune partie J de R
On appelle ainsi tout réel m
inférieur ou égal à chacun des éléments de J.
On dira aussi que J est minorée par m.
Borne inférieure dune partie minorée non vide J de R
Cest le plus grand des minorants de lensemble J. On peut déduire facilement
son existence de laxiome de la borne supérieure, en appliquant celui ci
à lensemble majoré J formé par tous les opposés des éléments de J.
On vérifie en effet sans peine que inf(J)=-sup(-J)
On peut maintenant énoncer et établir le théorÃme dit de limite croissante :
Soit f
une fonction à valeurs réelles, croissante sur lintervalle I=]a,b[.
( avec a et b éléments de ![]() ).
Une telle fonction admet toujours une limite en chacune des bornes de cet
intervalle I déterminée par :
).
Une telle fonction admet toujours une limite en chacune des bornes de cet
intervalle I déterminée par :
![]() si f(I)
est non majoré et
si f(I)
est non majoré et ![]() si f(I)
est majoré.
si f(I)
est majoré.
![]() si f(I)
est non minoré et
si f(I)
est non minoré et ![]() si f(I)
est minoré.
si f(I)
est minoré.
Preuve.
Etudions la fonction f au
voisinage de la borne supérieure b de
I.
_ Supposons f(I) non majoré. Pour tout réel M donné,
on pourra donc trouver un élément c de
I tel que f(c)
>M.
La fonction f étant supposée
croissante sur I, on en déduit que c<x <b Þ f(x) ³ f(c)
>M.
On peut donc rendre limage de x par f plus grande que le réel imposé M en
plaçant x suffisamment prÃs de
b. Ceci assure ![]()
_ Supposons maintenant f(I) majoré et notons l sa borne supérieure.
Pour tout e >0 donné, l- e
étant strictement inférieur au plus petit des majorants de f(I) ne sera pas un majorant
de cet ensemble.
On pourra donc trouver un élément c
de I pour lequel f(c)
>l-e.
En jouant comme précédemment sur la croissance de f on établit donc : c<x<b Þ l-e< f(x)£l.
On peut donc rendre f(x)
proche de l à nimporte quel e prÃs, à condition
de placer x dans un voisinage
convenable de b. On a donc bien
établi que ![]()
On effectue un schéma de démonstration analogue au voisinage de la borne a.
Dans le cas dune fonction décroissante sur I=]a,b[ on a un énoncé
similaire :
Soit f
une fonction à valeurs réelles, décroissante sur lintervalle I=]a,b[.
( avec a et b éléments de ![]() ).
Une telle fonction admet toujours une limite en chacune des bornes de cet
intervalle I déterminée par :
).
Une telle fonction admet toujours une limite en chacune des bornes de cet
intervalle I déterminée par :
![]() si f(I)
est non minoré et
si f(I)
est non minoré et ![]() si f(I)
est minoré.
si f(I)
est minoré.
![]() si f(I)
est non majoré et
si f(I)
est non majoré et ![]() si f(I)
est majoré.
si f(I)
est majoré.
La démonstration sobtient facilement en appliquant le théorÃme
précédent à la fonction g=-f.
La conjonction des deux énoncés est appelé simplement théorÃme de limite
monotone.
3) THEORIE DES EQUIVALENTS.
Rien de nouveau dans ce paragraphe au point de vue résultats fondamentaux.
Nous allons simplement introduire deux notations commodes décrivant des
situations classiques intervenant dans les problÃmes aux limites (
négligeabilité et équivalence), permettant dénoncer de façon concise la
plupart des résultats de base sur les fonctions usuelles et de les combiner de
maniÃre quasi- algébrique, sous réserve de bien dominer les
manipulations permises.
Cette démarche que nous développerons surtout dans les exercices accompagnant
le chapitre est le premier jalon de la théorie des approximations locales que
nous approfondirons aprÃs létude de la dérivation ( qui constitue aussi
une de ses facettes) et dont le point final sera pour nous lobtention des
développements limités, approximations locales à laide de polynômes .
Dans tout ce qui suit les fonctions seront supposées définies sur le mÃme
ensemble I de R et étudiées au voisinage dun
élément x0 de ![]() , adhérent à I.
, adhérent à I.
A)
Négligeabilité.
1) Définition et notation :
Nous dirons que la fonction g est négligeable devant f au voisinage de x0 si et seulement si il existe une fonction e telle quau voisinage de ce
point : g(x)=f(x).e(x) , avec ![]()
On dira pour simplifier que g est un
petit o de f et on écrira g=o(f) au V(x0) ou ![]()
ou encore g est un o(f) au V(x0).
2) PremiÃres remarques.
Dire que ![]() signifie quil existe
une fonction e de variable réelle et à valeurs
réelles et un voisinage V de x0
tels que : ( xII V g(x)= f(x)e(x) ) et (
signifie quil existe
une fonction e de variable réelle et à valeurs
réelles et un voisinage V de x0
tels que : ( xII V g(x)= f(x)e(x) ) et (![]() .)
.)
_ Si la fonction f est à
valeurs non nulles au voisinage de x0
, cest à dire sil existe un voisinage U de ce point tel que sur I U f(x) ¹ e(x) coÃncide alors nécessairement sur I V U avec le quotient ![]() .
.
On a dans ce cas léquivalence : ![]()
![]()
_ Si la restriction de f à I- est à valeurs non
nulles au voisinage de x0
et que f(x0)=g(x0)=0, e coÃncide encore sur (I-) U V avec le quotient de g par f et pourra Ãtre
prolongée en x0 en posant e(x0)=0. On a dans ce cas léquivalence : ![]()
![]()
Les résultats classiques concernant le comportement relatif des puissances,
logarithmes et exponentielles se traduisent alors :
|
a > |
a > |
Si b>a |
Si a>b |
3) RÃgles pratiques de simplification.
Grace aux théorÃmes de base concernant les fonctions de limite nulle
on démontre facilement les propriétés suivantes :
_ La somme de deux fonctions
négligeables devant f au voisinage de
x0 est aussi négligeable
devant f au voisinage de cet x0.
En effet si au V(x0)
on a ![]()
On en déduit au V(x0) :![]()
On pourra résumer cette rÃgle par la simplification : ![]()
_ Le produit dune fonction négligeable
devant u au V(x0) par une fonction négligeable devant v au V(x0) est négligeable devant le produit u.v au V(x0)
En effet de g(x)=u(x)a(x) avec ![]() et h(x)=v(x)b(x) avec
et h(x)=v(x)b(x) avec ![]() on déduit
immédiatement (g.h)(x)=(u.v)(x).(a(x).b(x)) avec
on déduit
immédiatement (g.h)(x)=(u.v)(x).(a(x).b(x)) avec ![]()
Ici aussi on pourra résumer par : ![]()
_ Si g
est négligeable devant f au V(x0), son produit par une
fonction quelconque j
(définie au V(x0) ) sera
négligeable devant le produit j.f au voisinage de x0.
De g(x)=f(x)a(x) avec ![]() on déduit en effet g(x)j(x)= f(x)j(x)a(x) avec
on déduit en effet g(x)j(x)= f(x)j(x)a(x) avec ![]() .
.
On résumera cette rÃgle par : ![]()
_ Notons pour terminer la relation de transitivité : Si h est négligeable devant g au V(x0) et g
négligeable devant f au V(x0), alors h est négligeable devant f au V(x0)
En effet, par hypothÃse h(x)=g(x)a(x)
et g(x)= f(x)b(x)
avec ![]()
On en déduit h(x)=f(x)a(x)b(x)
avec ![]()
Ecriture condensée : ![]()
B)
Equivalence.
1) Définition et notation :
Nous dirons que la fonction g est équivalente à f au voisinage de x0 si et seulement si il existe une fonction u telle quau voisinage de ce
point : g(x)=f(x).u(x) avec ![]()
On écrira en abrégé : g f au V(x0) ou encore ![]()
On pourra dire aussi : g
équivaut à f en x0.
2) Rapports avec la négligeabilité.
Dire quune fonction u tend vers 1 en
x0 revient à dire que
u=1+e avec e fonction de limite nulle en x0. Ainsi les fonctions
équivalentes à f en x0
sont celles définies au voisinage de ce point par une formule du type g(x)= f(x)(1+e(x))= f(x)+
f(x)e(x) avec ![]()
autrement dit les fonctions sommes de f
avec une fonction négligeable devant f
au V(x0).
On écrira pour résumer cela : Au
V(x0) g f g=f+o(f) .
Ainsi tout polynôme non nul est équivalent au voisinage de +¥ ou - ¥ a son terme dominant, puisque
somme de ce terme de degré maximal , soit anxn, avec des monômes de degré strictement
inférieur à n, donc
négligeables devant anxn.
_ Comme pour la négligeabilité, on obtient des définitions équivalentes
simplifiées dans le cas oà f ne sannule pas au voisinage de x0 : g f ![]() , ainsi que dans le cas oÃ
, ainsi que dans le cas oÃ
la restriction de f à I- ne sannule pas au V(x0) et oà f et g
sannulent simultanément en x0.
g f ![]()
Les études locales à lorigine effectuées sur les fonctions usuelles se
traduisent en termes déquivalents par les relations : Au V(0)
|
sin(x) x |
1-cos(x) |
ln(1+x) x |
(1+x)a-1 ax |
ex- x |
3) RÃgles usuelles demploi.
On vérifie trÃs facilement les rÃgles suivantes en utilisant les principaux résultats sur
les limites ou les propriétés de la négligeabilité étudiées précédemment.
_ Réflexivité. Toute fonction
équivaut à elle mÃme en tout point. f f .
_ Symétrie. Si g équivaut à f au
V(x0), alors f équivaut à g au V(x0). f g Þ g f .
_ Transitivité. Si au V(x0), h est équivalente à g
et g équivalente à f, alors h équivaut à f en x0
(h g et g f Þ h
f .
_ Produits, inverses, quotients.
Si au voisinage de x0 on
sait que u v et f g, on peut alors en déduire, au voisinage
de x0 :
|
u.f v.g |
|
|
|
(a représentant un exposant réel fixe
et sous réserve que les fonctions définies par les opérations ci dessus soient
effectivement définies au voisinage de x0)
_ Remplacement dun terme par un
équivalent dans une relation de négligeabilité.
Si au voisinage de x0, g est négligeable devant f, tout équivalent u à g en ce point
est négligeable devant tout équivalent v
à f.
Si au V(x0) : g=o(f)
, g u et f v
, alors on peut
conclure u =o(v) en ce point x0..
4) PiÃges à éviter.
En dehors des rÃgles évoquées précédemment, toute transformation portant
sur une relation déquivalence ou de négligeabilité doit Ãtre justifiée par un recours
rigoureux aux théorÃmes et définitions clefs sur les limites.
Léquivalence en un point x0
de deux fonctions f et g ne signifie pas que lon peut
remplacer f par g dans une étude locale en x0
oà interviennent des opérations quelconques mettant en jeu f.
Exemples :
_ Trouver un équivalent en +¥ de s(x)=![]()
On a bien sÃr f(x)=
![]() au voisinage de +¥ daprÃs la rÃgle
sur le quotient déquivalents alliée à celle sur le comportement des
polynômes à linfini.
au voisinage de +¥ daprÃs la rÃgle
sur le quotient déquivalents alliée à celle sur le comportement des
polynômes à linfini.
On peut Ãtre tenté de remplacer alors f(x)
par léquivalent élémentaire x ce qui
conduirait pour s(x) à léquivalent : x+2-x=2 en +¥.
Or la réduction au mÃme dénominateur conduit de maniÃre rigoureuse
à s(x)=![]()
On ne peut donc en rÃgle générale trouver un équivalent dune somme en
remplaçant un de ses termes par un équivalent.
_ Partons de la relation élémentaire : x²+x x² au voisinage de +¥. On serait tenté den déduire
que les exponentiels seront aussi équivalents en +¥.
Or ![]() doà lon
déduit que ex est en fait
négligeable devant
doà lon
déduit que ex est en fait
négligeable devant ![]() en +¥
en +¥
_ De mÃme x+p x en +¥ nentraine pas sin(x+p)=-sin(x)
sin(x) au voisinage de +¥.
_ De maniÃre générale u v au V(x0) ne permet pas de déduire pour une fonction
quelconque j ,
que j![]() u j
u j![]() v au voisinage de
ce mÃme point x0.
v au voisinage de
ce mÃme point x0.
_ Notons cependant un bon point pour le passage au logarithme, sous couvert
dune condition supplémentaire :
Si u
v en x0 et si ![]() avec pour l un élément quelconque de [0,+¥]-, alors on peut en déduire
quau V(x0) : ln(u) ln(v)
avec pour l un élément quelconque de [0,+¥]-, alors on peut en déduire
quau V(x0) : ln(u) ln(v)
(On suppose bien sÃr les fonctions strictement positives au voisinage de x0)
En effet, par hypothÃse, au voisinage de x0 : u(x)=v(x)l(x)
avec l de limite 1 en en x0.
On en déduit, toujours au V(x0),
que : ln(u(x))=ln(v(x))+ln(l(x)).
v(x)
tendant vers l ¹1 en x0 , on est sÃr que ln(v(x)) sera non nul sur un
voisinage de x0, ce qui
permettra décrire : ![]()
Or le numérateur ln(l(x)) tend vers ln(1)=0 en x0 et le dénominateur tend
vers ln(l)¹0 si l est un réel strictement positif distinct de 1, tend vers +¥ si l =+¥,
et enfin vers -¥
si l=0.
Dans les trois cas le quotient ![]() tend vers 0 en x0 .
tend vers 0 en x0 .
On a donc bien ln(u) ln(v) en ce point.
Par contre si l=1 le passage au ln
est illicite. Pour sen convaincre considérer par exemple léquivalence de ![]() et
et ![]() au voisinage de +¥, alors que le rapport des
logarithmes du deuxiÃme au premier tend vers 10.
au voisinage de +¥, alors que le rapport des
logarithmes du deuxiÃme au premier tend vers 10.
4) Changements de variable.
Si les compositions à gauche, cest à dire les actions sur les
images ne sont pas autorisées en général, par contre les compositions à
droite traduisant un changement de variable sont tout à fait licites,
ceci daprÃs le théorÃme de composition.
Par exemple si g est équivalente
à f au voisinage de x0 et si on effectue le
changement de variable x=j(t) tel que ![]() on peut en déduire que
g(j(t)) f j(t))
au V(t0)
on peut en déduire que
g(j(t)) f j(t))
au V(t0)
En effet par définition mÃme, au V(x0) :
g(x)= f(x)u(x)
avec u de limite 1 en x0
On en déduit aussitôt quau voisinage de t0 :
g(j(t))= f(j(t))u(j(t)) avec ![]()
On peut reproduire le mÃme schéma pour une relation de petit o.
Dans la pratique on renverra donc fréquemment les études locales proposées
à une analyse à lorigine 0 oà sont donnés les
développements des fonctions usuelles.
5) Fonctions équivalentes et fonctions de limites égales en un point.
Ces deux notions ont des liens mais sont loin dÃtre synonymes !
Ainsi deux fonctions tendant vers +¥ en x0 nont aucune raison de voir leur quotient
tendre vers 1, de mÃme si ces deux fonctions sont de limite nulle au
point détude.
Dans les situations envisagées nous sommes en effet dans les cas
dindétermination du quotient et les contre-exemples sont légion.
Par contre il est clair que si deux fonctions tendent vers une limite réelle l non nulle en x0,
chacune de ces fonctions sera équivalente à la constante l en x0
et donc par transitivité ces fonctions seront bien équivalentes eau point
considéré.
Notons pour finir le résultat évident montrant limpact de la notion
déquivalent dans le calcul pratique des limites :
Si g f au V(x0) et si f
tend vers l en x0 , alors on peut en déduire que g admet aussi l pour
limite en x0.
En effet, par hypothÃse, au V(x0) : g(x)=
f(x)u(x) avec u de limite 1 en x0
Il suffit ensuite dutiliser le théorÃme du produit.
Mais attention là encore, deux fonctions peuvent Ãtre équivalentes
au voisinage dun point sans quaucune nait une limite en ce point.
Considérer par exemple léquivalence au V(+¥) : ![]()
C)
Domination.
1) Définition et notation.
Nous dirons que la fonction g est dominée par f au voisinage de x0 si et seulement si on peut écrire au V(x0) g(x)= f(x)b(x) avec b fonction numérique bornée au voisinage de x0.
On dira que g est un grand O de f au voisinage de x0 et on écrira en abrégé g=O(f) au V(x0) ou également ![]()
Ici encore si f est à valeurs
non nulles au voisinage de x0
, on montre que la définition revient à dire que le quotient de g par f est borné au V(x0),
cest à dire quil existe un réel M > 0 et un voisinage V de x0 tel que xII V Þ 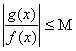
On établit alors sans difficultés les résultats suivants :
_ Si au V(x0) g=o(f)
ou g f, alors g =O(f)
_ Si f est bornée au voisinage de x0, alors au V(x0) : f=O(1)
_ Si au V(x0) h est un
o(g) et g un O(f), alors au V(x0) h
est un o(f). ![]()
_ Si au V(x0) h est un O(g) et g un o(f), alors au V(x0) h est un
o(f) ![]()
_ Le produit dun o(f) par un O(g) est un o(f.g). ![]()
_ Dans la pratique on utilisera surtout la remarque suivante :
Si b est bornée au voisinage de x0, alors tout produit par b dun o(f) est un o(f) et tout
petit o dun produit par b de f est aussi un o(f).
![]()
Les démonstrations trÃs faciles sont laissées en exercices.
Exercices sur les limites.
En
transformant convenablement les expressions proposées, résoudre les
problÃmes aux limites suivants :
a) ![]() b)
b) ![]() c)
c) ![]()
En
utilisant les propriétés algébriques classiques des logarithmes et
exponentielles, résoudre les problÃmes aux limites suivants :
a) ![]() b)
b) ![]() c)
c) ![]()
En
utilisant un changement de variable, étudier les problÃmes aux limites
suivants :
a) ![]() b)
b) ![]() c)
c) ![]()
Déterminer
les limites suivantes :
a) ![]() b)
b) ![]() c)
c) ![]()
Déterminer
les limites suivantes :
a) ![]() b)
b) ![]() c)
c) ![]()
On utilisera entre autres les équivalents classiques en 0 : ln(1+x) x ; ex-1 x ; 1-cos(x) ![]()
Déterminer
en utilisant les théorÃmes liés à lordre sur R, les limites suivantes :
a) ![]() b)
b) ![]() c)
c) ![]()
( E(x) désignant la partie entiÃre du réel x )
Montrer
que les fonctions définies par les formules suivantes nont pas de limites en +
¥ :
a) x(sin(x)+1) b) x4cos(x)+x3sin(x) c) x²-xE(x)
E(x)
désignant la partie entiÃre du réel x,
cest à dire le plus grand entier relatif inférieur ou égal à x, étudier les problÃmes aux
limites suivants :
a) 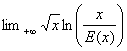 b)
b) ![]() c)
c) ![]()
On
admet lexistence dune limite réelle en 0 pour ![]()
a) En transformant convenablement f(2x), trouver la valeur de cette limite.
b) Utiliser le résultat précédent pour
déterminer 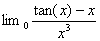 et
et 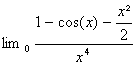
Simplifier en un seul o(x a) au voisinage proposé les
expressions :
a) o(x3)+o(x2) au V(0) et V(+¥) b) o(x3)o(x+1) au V(-¥) c) o(ln(x)+x3) au V(+¥)
d) o(x²ln(x)) au V(0) e) ![]() au V(0) et V(+¥
au V(0) et V(+¥
Pour chacune des fonctions
suivantes, déterminer un équivalent simple aux voisinages mentionnées :
a) ln(x)-3x au V(0) et V(+¥ b) x7-1 au V(0), V(+¥) et V(1).
c) ![]() au V(0 d) x+
au V(0 d) x+![]() sin(x) au V(0) et
V(+¥
sin(x) au V(0) et
V(+¥
MÃme exercice pour les
expressions :
a) 3x-2x au V(+¥), V(-¥) et V(0 b) tan(2x)-1+cos(x) au V(0)
c) x4+sin(x)-tan(x) au V(0) et V(![]() ). d) x3ln(cos(
). d) x3ln(cos(![]() )) au V(+¥
)) au V(+¥
Trouver un équivalent simple pour
les expressions :
a) 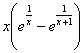 au V(+¥) , V(0+) et V(0-) b) cos(sin(x))-ex au V(0)
et V(+¥)
au V(+¥) , V(0+) et V(0-) b) cos(sin(x))-ex au V(0)
et V(+¥)
c) 3x-x3
au V(0), V(+¥)
et V(3). d) ![]() au V(+¥) et V(0)
au V(+¥) et V(0)
MÃme exercice pour les
expressions :
a) ![]() au V(+¥) et V(0). b)
au V(+¥) et V(0). b) ![]() au V(+¥) et V(0)
au V(+¥) et V(0)
c) ![]() au V(+¥) et V(0). d) ex+x100-(ln(x))1000 au V(+¥
au V(+¥) et V(0). d) ex+x100-(ln(x))1000 au V(+¥
MÃme exercice pour :
a) ![]() au V(
au V(![]() ) b)
) b) ![]() au V(1)
au V(1)
c) ![]() au V(0) et V(+¥ d)
au V(0) et V(+¥ d) ![]() au V(+¥) et V(0).
au V(+¥) et V(0).
On considÃre f(x)=![]() .
.
a) Trouver un équivalent simple de f(x) au voisinage de +¥ puis de f(x)-1 au V(0).
b) Montrer quau voisinage de +¥ f![]() f(x)=1-
f(x)=1-![]()
On considÃre f(x)=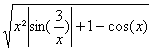
a) Trouver un équivalent simple de f(x)
au voisinage de +¥.
b) Montrer que f(x)
ne peut admettre au voisinage de 0 aucun équivalent du type mx a avec m et a
réels.
Choisir les réels a et b de façon quau
voisinage de 0, f(x)=![]() admette un équivalent du type mx3, avec m
réel à préciser.
admette un équivalent du type mx3, avec m
réel à préciser.
Déterminer des équivalents
simples pour les expressions suivantes :
a) ![]() au voisinage de
0. b)
au voisinage de
0. b) 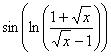 au voisinage de + ¥
au voisinage de + ¥
Etudier les problÃmes aux
limites suivants :
a) 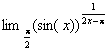 b) lim 0
sin(x)ln(1-cos(x)) c)
b) lim 0
sin(x)ln(1-cos(x)) c) ![]()
Exercices sur les limites. Solutions.
a)
![]() =
=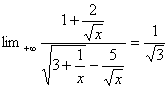 car
car ![]()
b) ![]() =
=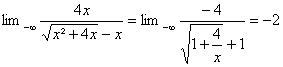 . Pour x <0
. Pour x <0 ![]()
c) ![]() =
=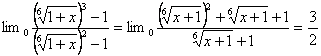
a)
![]() =
=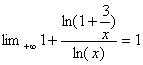
b) ![]() =
=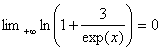
c) ![]() =
=![]()
Or : 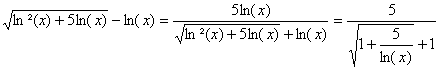 tend vers
tend vers ![]() lorsque x tend vers +¥. (ln(x) >0 au voisinage de +¥).
lorsque x tend vers +¥. (ln(x) >0 au voisinage de +¥).
Par continuité de la fonction exponentielle, on obtient donc ![]() pour la limite
étudiée.
pour la limite
étudiée.
a)
On pose X=![]() ce qui nous renvoie à létude de
ce qui nous renvoie à létude de ![]() .
.
1 étant racine du numérateur et du dénominateur, on termine en
factorisant :
![]() =
=![]()
b) En posant x=![]() +h, il vient :
tan(x)=
+h, il vient :
tan(x)=![]() et cos(2x)=-sin(2h). Lexpression étudiée se simplifie
alors en
et cos(2x)=-sin(2h). Lexpression étudiée se simplifie
alors en 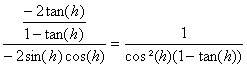 et tend vers 1
lorsque h tend vers 0. Ainsi
et tend vers 1
lorsque h tend vers 0. Ainsi ![]() =
=![]()
c) En posant x=![]() on obtient :
on obtient :
![]() et
et ![]() .
.
Ainsi ![]() =
=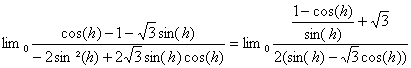
Or 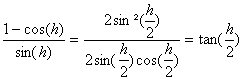 tend vers 0 lorsque h tend vers 0.
tend vers 0 lorsque h tend vers 0.
On obtient donc daprÃs les
rÃgles sur les opérations usuelles :![]() = -
= -![]()
a)
Lexpression donnée se simplifie facilement avec les formules de trigonométrie
élémentaire : ![]()
Elle admet donc pour limite ![]() en 0.
en 0.
b) ![]()
La limite de lexpression précédente au point 3 est donc égale à ![]()
c) ![]() avec X=
avec X=![]()
Comme ![]() , il vient donc :
, il vient donc : ![]() =ln(3)
=ln(3)
a)
![]()
Or 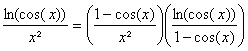
On sait que ![]() et que
et que ![]() .
.
On en déduit dabord par composition que ![]() , puis par la
rÃgle du produit :
, puis par la
rÃgle du produit : ![]() = -
= -![]()
b) 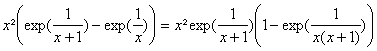
On sait que ![]() .
.
On en déduit, daprÃs le
théorÃme de composition, que : 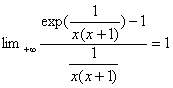 .
.
En écrivant lexpression étudiée sous la
forme : 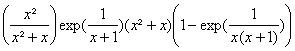 , on en déduit
daprÃs le théorÃme du produit que la limite en +¥ sera égale à 1.
, on en déduit
daprÃs le théorÃme du produit que la limite en +¥ sera égale à 1.
c) (x+1)ln(x+1)-xln(x)=xln(![]() +ln(x+1)=
+ln(x+1)=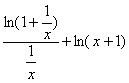
Le premier terme de cette somme tend vers 1 lorsque x tend vers +¥ car ln(1+X) X en 0.
Le deuxiÃme terme tend vers +¥, autre résultat classique sur la
fonction ln.
Ainsi : ![]() =+¥
=+¥
a)
Pour tout x réel on a évidemment cos(x) ³-1. On en déduit pour tout x réel positif la minoration : x(cos(x)+![]() )³
)³
![]() . La fonction étudiée tend vers +¥ lorsque x tend vers +¥.
. La fonction étudiée tend vers +¥ lorsque x tend vers +¥.
b) Pour x ³1 on sait que x ³![]() . Sur le voisinage [1,+¥] de +¥ on aura donc la
minoration :
. Sur le voisinage [1,+¥] de +¥ on aura donc la
minoration : ![]()
Or sin²(x)+cos4(x)=sin²(x)+(1-sin²(x))²=sin4(x)-sin²(x)+1=(sin²(x)-![]() )²+
)²+![]() ³
³![]()
Ainsi ![]() =+¥ daprÃs la minoration :
=+¥ daprÃs la minoration : ![]() , valable sur [1,+¥[ et parce que lim
, valable sur [1,+¥[ et parce que lim![]() =+¥.
=+¥.
c) DaprÃs la définition mÃme de la partie entiÃre dun
réel quelconque x, on a lencadrement
classique : x-1 < E(x) £ x.
On en déduit pour tout x >0 : x²-x+3 < xE(x)+3 £ x²+3.
De lencadrement élémentaire 1 £ sin(x)
£ 1 on déduit pour tout x >1 : ![]() .
.
Ainsi, par produit, et pour tout réel x
>1 on obtient lencadrement :
![]()
Puisque 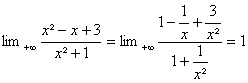 et que
et que 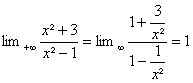
on en déduit, daprÃs le théorÃme dencadrement, que : ![]() =1
=1
a)
Posons f(x)=x(sin(x)+1).
_ Pour an=2np avec n entier on obtient f(an)=an
_ Pour bn=![]() +2np avec toujours n entier on a ici f(bn)=0.
+2np avec toujours n entier on a ici f(bn)=0.
On a donc mis en évidence deux suites de limite +¥ et telles que les suites des images par f admettent des limites différentes (lim+¥
f(an)=+¥ et lim+¥ f(bn)=0)
f nadmet donc pas de limite en +¥.
b) Posons g(x)= x4cos(x)+x3sin(x). En utilisant les deux suites
employées dans lexercice précédent on obtient : g(an) =(an)4 et g(bn)=-(bn)3.
Ici encore les limites des suites images diffÃrent : lim+¥g(an)=+¥ et lim+¥g(bn)=-¥
g nadmet donc pas non plus de limite
en +¥.
c) Posons h(x)=x²-xE(x)=x(x-E(x))
_ Pour an=n
avec n entier on obtient h(an)=0 , suite constante de limite
nulle.
_ Pour bn=n+![]() avec n entier,
il vient h(bn)=
avec n entier,
il vient h(bn)=![]() , suite qui tend vers +¥.
, suite qui tend vers +¥.
h nadmet donc pas de limite en +¥
a)
![]()
De x-1 <E(x) £x on déduit aussitôt ![]() pour tout x >1.
pour tout x >1.
On connait aussi lencadrement classique 0 £ln(1+X) £X valable pour tout X ³0.
En combinant les deux remarques précédentes il vient naturellement : x > £ln(![]() et par suite : 0 £
et par suite : 0 £ 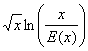
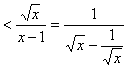
On conclut avec le théorÃme dencadrement : 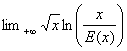 =0.
=0.
b) Posons f(x)=![]()
_ Pour an=n avec n entier, nous avons f(an)=an , suite divergent vers +¥.
_ Pour bn=n+![]() avec n entier non
nul, on obtient f(bn)=bncos(
avec n entier non
nul, on obtient f(bn)=bncos(![]() =bnsin(
=bnsin(![]()
Or bn n au voisinage de +¥ et sin(x) x au voisinage de 0. Il sensuit
daprÃs les rÃgles de composition et du produit, que f(bn) n(![]() )
) ![]() au voisinage de +¥.
au voisinage de +¥.
f(an) et f(bn) nayant pas le mÃme comportement
asymptotique en +¥, il sensuit que f nadmet pas de limite en +¥.
c) Posons g(x)=![]() et x=E(x)+r(x) pour tout réel x.
et x=E(x)+r(x) pour tout réel x.
On en déduit g(x)=xr(x)+E(x)cos²(p.r(x))³E(x)[r(x)+cos²(p.r(x))], car r(x) ³0.
En fait, r(x) excédent de x sur sa partie entiÃre, décrit
lintervalle [0,1[.
Il est facile de voir que sur cet intervalle, la fonction y ah(y)=y+cos²(py) est minorée par un réel
strictement positif.
En effet si y I[0,![]() ] on a 0 £py £
] on a 0 £py £![]() et par suite h(y)³
et par suite h(y)³![]()
Maintenant, si y I [![]() ,1[ il est évident que h(y)³
,1[ il est évident que h(y)³ ![]()
On a donc bien
y I[0,1[ , h(y)³ ![]() et par suite x IR+ g(x)³
et par suite x IR+ g(x)³ ![]()
On en déduit lim+¥g(x)=+¥
daprÃs la rÃgle de minoration, puisque lim+¥E(x)=+¥
a)
f(2x)=![]()
On a donc établi que pour x non nul, f(2x)=![]()
Notons l la limite supposée exister
et réelle de f(x)
en 0.
DaprÃs le théorÃme de composition on aura donc aussi lim 0 f(2x)=l.
On connait par ailleurs ![]()
En utilisant les rÃgles opératoires, les remarques ci dessus et
léquation fonctionnelle vérifiée par f,
on en déduit la relation aux limites l=![]() . La seule valeur possible pour la limite est donc l=-
. La seule valeur possible pour la limite est donc l=-![]() .
.
b) ![]() =
=![]()
Or au voisinage de 0, sin(x) x
et 1-cos(x) ![]() . Il sensuit
. Il sensuit ![]()
et par suite 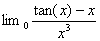 =l+
=l+![]()
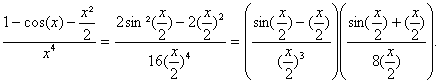
Ainsi 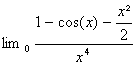 =
=![]()
a)_ Au voisinage de 0, x3 est un o(x²). Tout o(x3) est donc un o(o(x²))
donc aussi un o(x²)
Ainsi un o(x3)+o(x²) est une somme de deux fonctions
négligeables devant x² donc est
aussi un o(x²).
_ Au voisinage de +¥,
x² est un o(x3), tout o(x²)
sera un o(o(x3)) donc un
o(x3) et une somme du type
o(x²)+o(x3) peut Ãtre considérée comme un o(x3)+ o(x3) et donc aussi un o(x3).
b) Au voisinage de -¥
on sait que x+1 x. Tout o(x+1) est donc un o(x) et
un produit du type o(x+1)o(x3) sera un o(x). o(x3) et par suite un o(x4) daprÃs la rÃgle multiplicative.
c) Au voisinage de +¥,
ln(x) est négligeable devant toute
puissance positive de x.
Ainsi ln(x)+x3 x et tout o(ln(x)+x3) sera
aussi un o(x3).
d) Au voisinage de 0, ln(x) est
négligeable devant toute puissance xa
avec a<0.
Ainsi x²ln(x) est un o(x2-a) et tout o(x²ln(x)) est aussi
un o(x2-a) quel que soit a <0.
e) _ Au voisinage de 0, ln(1+x) x. On en déduit ![]()
![]() . Tout o(
. Tout o(![]() ) est donc un o(
) est donc un o(![]() ).En ce mÃme voisinage,
).En ce mÃme voisinage, ![]() 1 et
par suite tout o(
1 et
par suite tout o(![]() ) sera un o(1).
) sera un o(1).
On en conclut que toute somme du type o(![]() )+
)+![]() o(
o(![]() ) est un o(
) est un o(![]() )+o(
)+o(![]() ) donc encore un o(
) donc encore un o(![]() ).
).
_ Au voisinage de +¥,
ln(1+x) est équivalent à ln(x) donc est négligeable devant tout xa avec a
>0. Ainsi ![]() est un o(
est un o(![]() ) pour a >0. De mÃme x+ 1 x
ce qui entraine que tout o(
) pour a >0. De mÃme x+ 1 x
ce qui entraine que tout o(![]() ) est un o(x-1).
) est un o(x-1).
On en déduit que toute somme du type o(![]() )+
)+![]() o(
o(![]() ) sera aussi une somme
du genre o(
) sera aussi une somme
du genre o(![]() )+o(
)+o(![]() ) donc un o(
) donc un o(![]() ).
).
a) Au voisinage de 0, 3x de limite nulle est négligeable devant
ln(x) qui tend vers -¥.
On a donc ln(x)-3x du type ln(x)+o(ln(x)) équivalent à ln(x).
Au voisinage de +¥
on sait que ln(x) est négligeable
devant x .
Ainsi ln(x)-3x est du type -3x +o(3x) -3x.
b)_ En 0, x7-1 tend
vers le réel 1, donc est équivalent à cette limite réelle non nulle.
_ Au voisinage de +¥,
x7-1 est du type x7+o(x7) x7
_ Au voisinage de 1, la factorisation x7-1=(x-1)(x6+x5+x4+x3+x²+x+1) entraine léquivalence : x7-1 7(x-1)
car le facteur x6+x5+x4+x3+x²+x+1 tend vers 7 au point 1.
c) ![]() . Le dénominateur ayant pour limite 2
. Le dénominateur ayant pour limite 2![]() lorsque x tend
vers 0, on en déduit quau voisinage de 0 :
lorsque x tend
vers 0, on en déduit quau voisinage de 0 : ![]()
![]()
d)_ Au voisinage de 0 on sait que sin(x) x .On en déduit que sin(x)![]()
![]() et donc que la somme x+
sin(x)
et donc que la somme x+
sin(x)![]() est du type x+
est du type x+![]() +o(
+o(![]() ) ou encore de la forme x+o(x)+o(o(x)) car
) ou encore de la forme x+o(x)+o(o(x)) car ![]() est négligeable devant
x en 0. Ainsi en 0, x+ sin(x)
est négligeable devant
x en 0. Ainsi en 0, x+ sin(x)![]() x
x
_ Au voisinage de +¥,
![]() est négligeable devant
x, de mÃme que sin(x)
est négligeable devant
x, de mÃme que sin(x)![]() puisque sinus est une fonction bornée. On a donc x+ sin(x)
puisque sinus est une fonction bornée. On a donc x+ sin(x)![]() du type x+o(x) x
du type x+o(x) x
a) 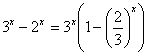 et
et 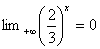 .
.
On en déduit quau voisinage de +¥ , ![]() 3x
3x
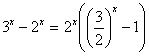 et
et ![]() Donc, au voisinage de
-¥,
Donc, au voisinage de
-¥, ![]() -2x
-2x
_ Pour létude en 0, partons du développement classique : ex=1+x+o(x)
On en déduit 3x=![]() ainsi que 2x=
ainsi que 2x=![]()
Ce qui nous donne : 3x-2x=x(ln(3)-ln(2))+o(x) x(ln(3)-ln(2))
b) On sait quau voisinage de 0, tan(x) x et 1-cos(x) ![]() . On en déduit le développement :
. On en déduit le développement :
tan(2x)-1+cos(x)=2x+o(x)-![]() +o(x²).
+o(x²).
Or x² est négligeable devant x en 0, ce qui conduit à
lécriture tan(2x)-1+cos(x)=2x+o(x) 2x
c) sin(x)-tan(x)=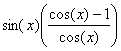 équivaut au voisinage de 0 à -
équivaut au voisinage de 0 à -![]() daprÃs les équivalents élémentaires et les
rÃgles concernant les produits et quotients.
daprÃs les équivalents élémentaires et les
rÃgles concernant les produits et quotients.
Ainsi, x4+sin(x)-tan(x)=x4-![]() +o(x3) -
+o(x3) - ![]() car au voisinage de 0
, x4 est un o(x3).
car au voisinage de 0
, x4 est un o(x3).
Au voisinage de ![]() , x4 et
sin(x) sont bornées, alors que
, x4 et
sin(x) sont bornées, alors que ![]()
On en déduit immédiatement que x4+sin(x)-tan(x)=-tan(x)+o(tan(x)) -tan(x)
d) Partons du développement classique au voisinage de 0 : cos(X)=1-![]() +o(X²)
+o(X²)
On en déduit quau voisinage de +¥, ![]() .
.
Utilisons maintenant le développement au voisinage de 0 : ln(1+X)=X+o(X)
Grace au changement X=-![]() on en déduit, au voisinage de +¥ , la relation :
on en déduit, au voisinage de +¥ , la relation :
ln(![]() )= -
)= -![]() +o(-
+o(-![]() )=-
)=-![]() +
+![]() -
-![]()
Finalement x3ln(![]() ) -
) -![]() au voisinage de +¥
au voisinage de +¥
a) Ecrivons 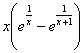 =
=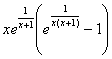
De léquivalence usuelle eX-1 X , valable au voisinage de 0, on
tire 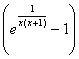
![]() au voisinage cette fois de +¥. Comme
au voisinage cette fois de +¥. Comme ![]() on en déduit
on en déduit 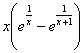
![]()
![]()
_ ![]() , alors que
, alors que ![]() tend vers 0.
tend vers 0.
On en déduit quau V(0+), 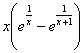
![]()
_ Lorsque x tend vers 0 par valeurs
négatives, 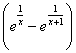 tend vers le réel non
nul e.
tend vers le réel non
nul e.
Donc au V(0-), 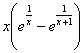 -ex
-ex
b) _ Au voisinage de 0, daprÃs les développements usuels, on peut
écrire :
cos(sin(x))-ex=cos(x+o(x))-1-x+o(x)=1-![]() -1-x+o(x)
-1-x+o(x)
AprÃs simplifications, il reste : cos(sin(x))-ex= -x-![]() +o(x)+o(x²) -x
+o(x)+o(x²) -x
_ Au voisinage de +¥,
cos(sin(x)) est borné alors que ex
tend vers +¥.
Ainsi cos(sin(x))-ex -ex
c) _ lim0 3x-x3=1 , réel non nul, donc 3x-x3 1 au V(0)
_ On sait quau V(+¥)
, X 3 est négligeable
devant eX. On en déduit
que x3=o(![]() ) et que par suite, toujours au V(+¥) : 3x-x3 3x.
) et que par suite, toujours au V(+¥) : 3x-x3 3x.
_ Pour létude au voisinage de 3, posons x=3+h. On obtient la nouvelle forme :
3x-x3=27(3h)-(27+27h+9h²+h3)=27(3h-1)-27h+o(h)
Or 3h-1=![]() =hln(3)+o(h) au voisinage de 0.
=hln(3)+o(h) au voisinage de 0.
On obtient donc finalement léquivalence : 3x-x3 27(ln(3)-1)(x-3) au V(3)
d) _ Au voisinage de +¥, ![]() =
=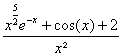
![]()
En effet ![]() tend vers 0 pour x tendant vers +¥ donc est négligeable devant cos(x)+2 qui est toujours supérieur ou égal
à 1.
tend vers 0 pour x tendant vers +¥ donc est négligeable devant cos(x)+2 qui est toujours supérieur ou égal
à 1.
_ Au voisinage de 0, le numérateur de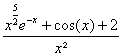 tend vers le réel non nul 3, doà lon tire :
tend vers le réel non nul 3, doà lon tire : ![]()
![]()
a) ![]() =
=![]()
_ Au voisinage de +¥,
ln(x) est négligeable devant x et toute puissance de x est négligeable devant ex. On en déduit
immédiatement que ![]()
![]()
_ Lorsque x tend vers 0, le numérateur
de la mÃme fraction étudiée tend vers 1.
Doà léquivalence au voisinage de 0 : ![]()
![]()
b) Il sagit dun quotient, étudions donc séparément numérateur et
dénominateur.
_ Au V(+¥),
ln(x)+x=x+o(x) x
. Et ln(ex+1)-ln(2)=x+ln(1+e-x)-ln(2) x
Le quotient est donc équivalent à 1 au voisinage de +¥.
_ Au V(0), ln(x)+x=ln(x)+o(ln(x)) ln(x).
ln(ex+1)-ln(2)=![]() =
=![]()
![]()
Ainsi le quotient équivaut au voisinage de 0 à 2![]()
c) Pour x >0, ![]() =
=![]()
Du développement usuel au voisinage de 0, ![]() on tire alors au
voisinage de +¥ :
on tire alors au
voisinage de +¥ :
![]() et
et ![]()
On en déduit ![]() =x²(
=x²(![]() x -3-x 2+o(x 3)+o(x
2)) -1
car x 3 est un
o(x 2) au voisinage de +¥.
x -3-x 2+o(x 3)+o(x
2)) -1
car x 3 est un
o(x 2) au voisinage de +¥.
_ Au voisinage de 0, x4+3x 3x,
donc ![]()
![]() .
.
De plus il est clair que ![]() x
x![]() .
.
On a donc ![]()
![]() car x est
négligeable devant
car x est
négligeable devant ![]() au V(0).
au V(0).
d) ln(x) est négligeable devant x au voisinage de +¥ et toute puissance de x est négligeable devant ex toujours en V(+¥) .
On en déduit facilement quen ce mÃme voisinage: ex+x100-(ln(x))1000 =ex+o(ex)+o(ex) ex
a) En posant x=![]() on obtient :
on obtient : ![]() =
=![]()
_ Le numérateur équivaut pour h
voisin de 0 à -3h
_ Le dénominateur se développe au voisinage de 0 en ![]() et équivaut donc
à
et équivaut donc
à ![]() .
.
DaprÃs la rÃgle du quotient on a donc au V(![]() ) :
) : ![]() -
-![]()
b) Pour létude au voisinage de 1 nous poserons x=1+h avec ici h <0 vu la racine.
Ainsi au voisinage de 0 : ![]()
![]() =
=![]()
Et au voisinage de 1 : ![]()
![]()
c) ![]() =exp(
=exp(![]() )
)
_ Au voisinage de 0, ln(ex+x)=ln(1+x+o(x)+x) 2x.
Le quotient par x équivaut alors
à 2 et tend vers ce réel pour x
tendant vers 0. Par continuité de lexponentielle la fonction étudiée a donc
pour limite e2 en 0 et
équivaut donc à ce réel non nul au voisinage considéré.
_ Au voisinage de +¥
on peut écrire ln(ex+x)=x+ln(1+xe-x) x, car lim+¥ ln(1+xe-x)=0.
Le quotient par x équivaut donc
à 1 et la fonction étudiée tend vers e1
au voisinage de +¥,
toujours par continuité de lexponentielle, donc équivaut à ce réel non
nul e.
d) ![]() =
=![]()
_ Au voisinage de +¥
le numérateur précédent équivaut à x2ex et le dénominateur
à x.
Il sensuit que le quotient est équivalent à xex
_ Au voisinage de 0, le numérateur équivaut à x2 et le dénominateur à ln(x), le quotient est donc équivalent à ![]()
a) _ Pour x >0,
![]() =x(
=x(![]() )
)
Utilisons le développement classique au voisinage de 0 : ![]()
On en déduit au V(+¥) :
![]() =
=![]()
![]() et donc
et donc ![]()
![]()
_ Au voisinage de 0, on a directement ![]()
On en déduit que f(x)-1=
-x+![]() x4+o(x4) -x au voisinage de 0.
x4+o(x4) -x au voisinage de 0.
b) f![]() f(x)=f(X)
avec X= f(x) qui tend vers 0 lorsque x
tend vers +¥
daprÃs le a)
f(x)=f(X)
avec X= f(x) qui tend vers 0 lorsque x
tend vers +¥
daprÃs le a)
On peut donc écrire f(X)=1-X+o(X) , ceci daprÃs
léquivalence en 0 de f(X)-1.
Or X=f(x)= ![]() +o(x-3)
pour x voisin de +¥.
+o(x-3)
pour x voisin de +¥.
Par composition on a donc finalement, toujours au voisinage de +¥ :
f![]() f(x)=1-
f(x)=1-![]() +
+![]() =1-
=1-![]()
a) De sin(X) X au voisinage de 0 on tire sin(![]() )
) ![]() au voisinage de +¥ et par suite
au voisinage de +¥ et par suite
x²![]() 3x et admet donc pour limite +¥ pour x
tendant vers +¥.
3x et admet donc pour limite +¥ pour x
tendant vers +¥.
1-cos(x) étant borné est négligeable
devant toute fonction tendant vers linfini, ce qui assure x²![]() +1-cos(x)
équivalent à 3x au V(+¥).
+1-cos(x)
équivalent à 3x au V(+¥).
En prenant la racine, on en déduit f(x) ![]() au voisinage de +¥.
au voisinage de +¥.
b) supposons quau voisinage de 0, f(x)=mxa +o(xa). On en déduit par élévation au carré et
développement élémentaire de cos(x)
une écriture du type :
x²![]() +
+![]() .
.
En divisant par x² il vient,
toujours au V(0) : ![]() +
+![]()
Or les deux membres de cette égalité sont incompatibles, le premier nadmettant
pas de limite en 0, alors que le deuxiÃme tend vers 0 si a >1, vers +¥ si a<1
et vers m² si a=1.
On sait quau voisinage de 0, ![]() .
.
f(x)=![]() ne peut donc admettre en 0 un équivalent du type mx3 que si a=
ne peut donc admettre en 0 un équivalent du type mx3 que si a=![]() . Etudions alors la différence d(x)=
. Etudions alors la différence d(x)=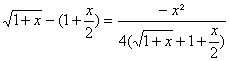
Celle ci équivaut au voisinage de 0 à -![]() , ce qui montre que la seule valeur possible pour le
paramÃtre b est -
, ce qui montre que la seule valeur possible pour le
paramÃtre b est -![]() .
.
Formons alors la différence f(x)=d(x)+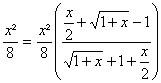
Lexamen rapide du comportement des numérateurs et dénominateurs au voisinage
de 0 nous montre que f(x)
est bien équivalent à un multiple de x3.
Plus précisément, on obtient f(x) ![]() .
.
a) ![]() =
=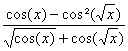
![]() au voisinage de 0.
au voisinage de 0.
Le développement usuel de cos au voisinage de 0 donne alors :
cos(x)=1-![]() et
et ![]() .
.
On en déduit cos²(![]() =1-x+o(x), puis cos(x)-cos²(
=1-x+o(x), puis cos(x)-cos²(![]() =x+o(x) x , ceci toujours au V(0)
=x+o(x) x , ceci toujours au V(0)
On conclut donc ![]()
![]() au voisinage de 0.
au voisinage de 0.
b) 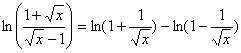
A partir du développement élémentaire ln(1+X)=X+o(X) au voisinage de 0, on
obtient donc avec ce qui précÃde, et au voisinage de +¥ : 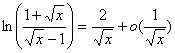
Enfin, de léquivalence élémentaire sin(X) X au voisinage de 0, on tire par
composition avec la relation précédente : sin(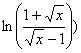
![]()
![]() au V(+¥
au V(+¥
a) ![]() .
.
Posons x=![]() pour se ramener à une étude au voisinage de 0.
pour se ramener à une étude au voisinage de 0.
![]()
![]()
![]() .
.
Donc la fonction étudiée tend vers e0=1 lorsque x tend vers ![]() , par continuité de la fonction exponentielle.
, par continuité de la fonction exponentielle.
b) Au voisinage de 0, sin(x)ln(1-cos(x)) xln(![]() 2xln
2xln![]()
Cette fonction est donc de limite nulle en 0.
c) Posons x=e+h pour se ramener
à une étude à lorigine.
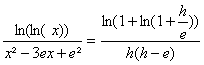
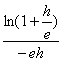
![]() .
.
La fonction étudiée a donc pour limite ![]() en e.
en e.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 959
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved