| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
| Autó | élelmiszer | épület | Földrajz | Gazdaság | Kémia | Marketing | Matematika |
| Oktatás | Orvostudomány | Pszichológia | Sport | Számítógépek | Technika |
DOCUMENTE SIMILARE |
|
Lineáris tagok jelátvivő tulajdonságait jellemző függvények
Az irányítási rendszer analízisében és szintézisében az állapotegyenleteken kívül nagy jelentőségük van azoknak a függvényeknek, amelyek az állapotváltozók mellőzésével különböző módon a ki- és a bemenő jelek közötti kapcsolatot írják le az idő ill. a frekvencia tartományban.
Az időtartományban egy tagot – differenciál- vagy differenciaegyenletén kívül – meghatározott bemenő jelekkel előidézett kimenő jelével is lehet jellemezni.
Különleges jelentősége van a Dirac delta (d(t)) bemenetre adott válasznak, az un. súlyfüggvénynek (y(t)), amelynek ismeretében a konvolúciós integrállal tetszőleges bemenő jellel gerjesztett kimenő jel is kiszámítható, másrészt a magára hagyott rendszer mozgásjellemzőit is tisztán mutatja, tehát a stabilitási viszonyok vizsgálhatók.
A vizsgálatokra a súlyfüggvény mellett nagy jelentősége van az egységugrás bemenetre adott válasznak, a h(t) átmeneti függvénynek. A h(t) átmeneti függvény segítségével specifikálhatók a szabályozórendszer paraméterei.
Átviteli függvény
A frekvencia tartományban az xk kimenő és az xb bemenő jel Laplace ill. z transzformáltjának a hányadosa az átviteli függvény, ill. az impulzus átviteli függvény, amely a folytonos idejű y ill. diszkrét idejű yd súlyfüggvény Y(s) ill. Yd(z) Laplace, ill. z transzformáltja.
Folytonos idejű n - tárolós tagra az átviteli függvény felírásához a differenciál egyenletből kell kiindulnunk:
![]() .
.
A differenciálegyenlet L transzformált alakja:
![]() .
.
A kimenő jel és a bemenő jel Laplace transzformáltjainak a hányadosa az s változó valós együtthatójú racionális törtfüggvénye:
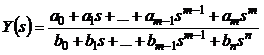 ,
,
amelyet a jelátviteli tag átviteli függvényének nevezünk.
Fizikailag realizálható rendszerre: m≤n.
Az átviteli függvény segítségével tetszőleges bemenő jel esetén felírható a kimenőjel Laplace transzformáltja:
![]() .
.
Az időfüggvényt ennek inverz Laplace transzformáltjaként kapjuk:
![]()
A számlálónak és a nevezőnek valós vagy konjugált komplex gyökei vannak. Jelölje a számláló gyökeit – a függvény zérusait – sz1……szm, a nevező gyökeit – a függvény pólusait – s1…….sn.. Az Y(s) átviteli függvény gyöktényezős formája:
![]()
Sokszor előnyösebb a gyökök negatív reciprokát – az időállandókat használni.
 ,
, ![]()
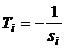 jelölésekkel:
jelölésekkel:
![]() .
.
Ez az átalakítás az szi=0 zérusok és az si=0 pólusok gyöktényezőiben nem hajtható végre, azokat eredeti alakjukban kell megőrizni. Ha a gyöktényezős alakban is csak valós együtthatókat kívánunk szerepeltetni, a konjugált komplex gyök párokat egy másodfokú valós együtthatójú tényezővé kell összevonni.
Legyen pl. si konjugáltja![]() , és Ti konjugáltja
, és Ti konjugáltja ![]() ,
,
![]()

![]() ;
;
![]() ;
;
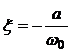
t a négyzetes tag sajátfrekvenciájának (natural frequency), ξ-t a csillapítási tényezőjének (damping factor) nevezik. A számláló konjugált komplex gyökeit hasonló módon másodrendű tényezőkben összevonva és megkülönböztetésül a τ0 ill. ζ jelöléseket használva az egyenlet az alábbi alakba írható:
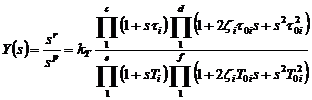 =
= ![]()
r+c+d=m és p+e+f=n;
Itt az összes időállandó és csillapítási tényező valós érték
Az r és p értékek viszonya szerint különböztetjük meg az Y(s) átviteli függvény ill. tag típusát. Az i=r-p jelöléssel:
r > p; Y(s) = si Yp(s), differenciáló típusú átviteli tag,
r = p Y(s) = Yp(s) arányos tag,
r < p Y(s) = s-iYp(s) integráló tag.
A kimenő jelben ezek a műveletek akkor jelennek meg tisztán, amikor a bemenő jel által kiváltott tranziensek már lecsillapodnak.
A tranzienseket az YP(s) függvény írja le. Ennek a szétválasztásnak az alapján úgy tekinthetjük, hogy egy tag tartós karakterének az érvényre jutását a tárolók feltöltődésével összefüggő hatások késleltetik. YP(s) az arányos időkéséses tag átviteli függvénye.
A tárolók feltöltődésén kívül a késleltetésnek egy másik forrása a jelhordozó véges terjedési sebessége, amely a ki és a bemenő jel közé egy Th idejű késleltetést – holtidős késleltetést – iktat.
A holtidős tag kimenő és bemenő jele közötti összefüggés az 1. ábra alapján
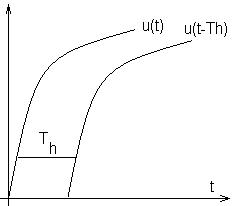
1. ábra: holtidős tag bemeneti és kimeneti jele.
A Laplace transzformáció eltolási szabályával:
![]()
Az átviteli függvény nem racionális tört, hanem transzcendens függvény. A racionális törtfüggvényeknek megfelelő differenciálegyenletek végtelen jelterjedési sebességet tételeznek fel (a véges terjedési sebesség parciális differenciálegyenletre vezet). Ezért folytonos idejű rendszerek állapotegyenletébe a holtidő csak közelítéssel iktatható be, vagy úgy, hogy a késleltetés hatását racionális törtfüggvénnyel – tárolós tagokkal – helyettesítjük, vagy a ki- ill. a bemenő jel késleltetéseként vesszük figyelembe, amelyhez azonban állapotváltozó nem rendelhető.
A holtidő minden reális rendszerben jelen van, hatása azonban csak akkor jelentős, ha a rendszerben végbemenő változások ideje a holtidővel összemérhető. Villamos jelek véges terjedési sebességéből eredő hatásokat csak kivételes esetekben (ultra nagyfrekvenciás jelenségek igen nagy távolságú – pl. bolygóközi – jeltovábbítása) kell figyelembe venni.
Egyéb anyag- ill. energiaáramlási jelenségek leírásakor a holtidő nem hanyagolható el (szállítószalagon, vagy csővezetéken történő anyagtovábbítás, hőáramlás, stb.)
Diszkrét idejű rendszerekben az állapotváltozók egy lépésköznyi holtidős késleltetést okozó tagokhoz vannak rendelve. Amennyiben a holtidő a mintavételezési idő egész számú többszöröse, véges számú állapotváltozóval leírható, így szervesen beilleszthető akár az állapotegyenletbe, akár az impulzus átviteli függvénybe. A holtidős tag impulzus átviteli függvénye:
Yhd (z)=z-h
h=Th/Ts=egész.
Az átmeneti függvény
Az időtartományban a tag tranziens tulajdonságai a legtisztábban a súlyfüggvényben és az átmeneti függvényben mutatkoznak. (Ez utóbbi a bemenő jelnek könnyebb kísérleti realizálhatósága miatt egyes esetekben előnyösebb).
Az átmeneti függvény Laplace transzformáltjából látható, hogy az a súlyfüggvényből integrálással képezhető.
![]() ;
; 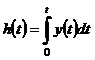
h(t) egyes tulajdonságai Y(s) – ből inverz transzformáció nélkül közvetlenül is láthatók.
számlálója és nevezője közötti fokszám különbségtől függnek.
A végérték tétellel:
![]()
és hasonlóan az r-edik differenciálhányadosra
![]()
Ha s minden határon túl növekszik, Y(s) számlálójában és nevezőjében a legnagyobb hatványok dominálnak. (6.1) jelölésével
![]()
Ha Y(s) számlálójának és nevezőjének (n-m) fokszám különbsége r, a h(t) függvény első (r-1) deriváltjának – magát a függvényt, mint 0-ik deriváltat is beleértve – a kezdeti értéke zérus.
Ha fokszám különbség 1, a t=0 pontban h(t) véges meredekséggel indul, ha 2, akkor a kezdeti érintő zérus hajlásszögű, ha több, a görbe egyre magasabb fokúan simul az időtengelyhez.
Azonos fokszámnál – ami annak a jele, hogy a bemenő jel közvetlenül hat a kimenetre – a h(t) függvénynek ugrása van a kezdőpontban.
a.) Az átmeneti függvény állandósult értéke, feltételezve, hogy YP(s) összes pólusának negatív valós része van.
![]()
Differenciáló tagra h(∞)=0, integrálóra h(∞)=∞, míg az arányos típusúra v(∞)=kT. Ez utóbbit ezért önbeálló tagnak is szokás nevezni.
Diszkrét idejű rendszerek átviteli függvénye
Az előzőekben láttuk, hogy a folytonos idejű jelátviteli tag n-ed rendű differenciál egyenlettel adható meg:
![]() .
.
A differenciálegyenlet Laplace transzformáltja segítségével definiáltuk az átviteli függvényt, mint a kimenő és a bemenő jel Laplace transzformáltjainak hányadosát:
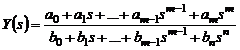 ,
,
A diszkrét idejű jelátviteli tag differencia
egyenletével írható le. Mivel a mintavételezés állandó T0
mintavételezési idővel történik, ![]() helyett egyszerűen k jelölést használhatunk, amely a
k-ik mintavett értéket jelöli. Az egyszerűsített jelöléssel az m-ed
rendű differencia egyenlet általános alakban a következő formában
írható:
helyett egyszerűen k jelölést használhatunk, amely a
k-ik mintavett értéket jelöli. Az egyszerűsített jelöléssel az m-ed
rendű differencia egyenlet általános alakban a következő formában
írható:
![]()
Az aktuális kimenet a k-ik időpillanatban a következő képlettel határozható meg:
![]()
A differencia egyenlet z transzformáltját írjuk fel:
![]()
Írjuk fel a kimenő jel és a bemenőjel hányadosát:
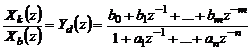
Az Yd(z) diszkrét idejű átviteli függvény a folytonos idejű jelátviteli tag átviteli függvényéhez hasonlóan leírja, hogy a diszkrét idejű tag a bemeneti jelsorozatból hogyan állítja elő a kimeneti jelsorozatot.
Példa:
Tekintsük az átlagoló egyenletét:
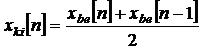
Helyettesítsük a tagokkal a z transzformáltjukkal:
![]()
A processzor blokkvázlata:

a.
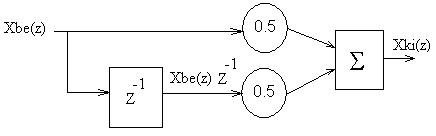
b.
![]()
A processzor diszkrét átviteli függvényét kapjuk, ha a kimenő jel és a bemenő jel hányadosát képezzük:
![]()
A processzor átviteli függvénye. Általában z pozitív hatványaival fejezzük ki:
![]()
Az Yd(z) átviteli függvény rendszerjellemző, megadja, hogyan állítja elő a processzor a kimenő jelsorozatot a bemenő jelsorozatból. Ha adott az átviteli függvény, a bemenő jelsorozatból előállítható a kimenő jelsorozat, hasonlóan, mint folytonos idejű tagok esetén:
![]()
Ha a bemenő jel a mintavételezett egység impulzus, d[n], a kimenet az egység impulzus válasz függvény, y[n] lesz. A z transzformáltakkal:
![]()
Egy lineáris diszkrét idejű processzor átviteli függvénye egyenlő a mintavételezett egység impulzusra adott válasz függvénnyel:
![]()
Példa:
ha ![]() , akkor
, akkor
![]()
Példa:
A processzor az alábbi lineáris differencia egyenlettel adott:
![]()
Határozzuk meg az átviteli függvényét és írjuk le a mintavételezett egység impulzusra adott választ.
![]()
![]()
![]()
![]()
példa:
Írjuk fel az átviteli függvényt, ha a lineáris differencia egyenlet:
![]()
Megoldás:
![]()
![]()
Példa:
A mintavételezett egységimpulzusra adott válasz:
![]()
Az átviteli függvény ebből felírható:
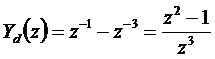
Rendszer válasz.
Ha ismert az Y(z) átviteli függvény és az xbe(z) bemeneti jelsorozat, az Xki(z) kimeneti jelsorozat előállítható Xki(z)=Y(z)Xbe(z) formában.
Példa:
legyen
![]() és
és
![]()
Határozzuk meg a kimeneti impulzussorozatot!
![]()
![]()
A kimeneti jelsorozat pedig:
![]()
A szorzás részeredményei:
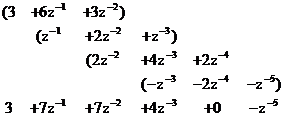
![]()
![]()
A módszer láthatóan nagy előnye, hogy konvolúció helyett szorzással kaphatjuk meg a kimenő jelet.
Példa:
Legyen a bemeneti jelsorozat:
![]()
Az egység impulzusra adott válasz:
![]()
Határozzuk meg a kimenő jelsorozatot!
![]()
![]()
![]()
![]()
Példa.
Végtelen jelsorozatok
A gyakorlati esetek egy részében a jelek végtelen sorozatot alkotnak. Tekintsünk egy rekurzív processzort, amely az alábbi differencia egyenlettel adott:
![]()
A z transzformált:
![]()
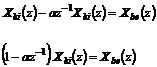
![]()
Az eredmény eltér az eddigiektől, és nem látható nyilvánvalóan, hogyan van kapcsolatban a mintavételezéssel és az y[n] függvénnyel. Egy módszer ehhez, ha kifejezzük Y(z)-t hatványsorozat formában:
![]()
Ebből már látható, hogy:
![]()
végtelen mintavételezett sor. Igy:
![]()
Ily módon egy végtelen sorozat z transzformáltját kifejeztük, mint z tört függvényét. Bizonyos feltételek esetén minden végtelen sorozat kifejezhető így, különösen, ha ismerjük a mintavételezett jel matematikai alakját.
Példa
vegyük az ![]() függvényt. Mi lesz a
z transzformáltja?
függvényt. Mi lesz a
z transzformáltja?
Helyettesítsük a mintavételezett jelekkel:
![]()
Helyettesítsünk: ![]()
![]()
A mintavételezett jel transzformáltja tartalmazza T-t exlplicit formában, ez azt mutatja, hogy T befolyásolja a mintavételezett értéket.
Példa:
egy egységugrás függvényt T s-al mintavételezünk. Írjuk fel a z transzformáltat, ha t=0 esetén a függvény értéke1!
![]() , ha
, ha ![]()
![]() , ha
, ha ![]() < 0
< 0
![]()
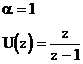
Ha az egységugrás t 1 mintavételezéssel késleltetjük:
![]()
![]()
A gyakorlatban sok függvénynek megvan a z transzformáltja táblázatban, ezért csak vissza kell keresni.
Pl táblázatból:
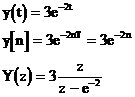
A táblázat, hasonlóan a Laplace transzformációhoz, csak az alap transzformációkat tartalmazza. Ez esetben is a Laplace transzformációhoz hasonló módon lehet a visszatranszformálthoz hozzájutni.
Példa:
![]()
Mi az egységugrásra adott válasz?
Az egységugrás z transzformáltja táblázatból:
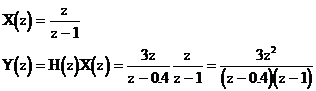
Parciális törtekre bontással végezzük e a visszatranszformálást:
![]()
A megoldás részletezésének a mellőzésével:
A= -2, B=5
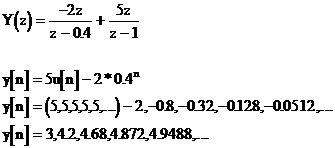
Az impulzusok 5-höz tartanak.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1984
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved