| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
| Autó | élelmiszer | épület | Földrajz | Gazdaság | Kémia | Marketing | Matematika |
| Oktatás | Orvostudomány | Pszichológia | Sport | Számítógépek | Technika |
DOCUMENTE SIMILARE |
|
Mintavételes rendszerek.
Mintavételezés
A digitális számítógépek irányítástechnikai felhasználsának két fő területe van:
a. Digitális szimuláció, amikor az irányítási rendszert számítógépen modellezik
b. Digitális irányítás, amikor az irányítás szerves része a számítógép, vagy annak egyes feladatait átveszi.
A digitális adatfeldolgozó rendszerekben a jeleket mintavételezzük, majd digitalizáljuk. Eredményül diszkrét jelet kapunk, amelyek amplitúdóban és időben kvantáltak. Ezt a folyamatot a 4.1. ábra szemlélteti. Az analóg jelektől eltérően, az így előállított jeleknek csak diszkrét időpillanatban vannak értékei, amelyek szintén diszkrétek. A folyamat eredményeképpen amplitúdó modulált impulzus sorozat jött létre, amelyben az állandó ti szélességű impulzusok amplitúdója, illetve az impulzusok területe arányos a folytonos jel amplitúdójával. A közelítés annál pontosabb, minél kisebb a mintavételi periódus idő.
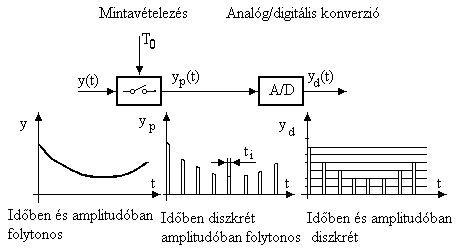
4.1: ábra: Diszkretizálás időben és amplitúdóban.
Az amplitúdó felfelé vagy lefelé van kerekítve az amplitúdó kvantálás eredményeképpen. A mintavételezés általában állandó To mintavételi periódus idővel történik. A digitalizált jel a mikroprocesszor bemeneti adata lesz, amely a kimenő jelet a programozott jelfeldolgozó algoritmusnak megfelelően állítja elő. Ha a beavatkozó szerv analóg jelet igényel, a kimeneti jelet D/A átalakító és tartó eszköz segítségével visszaalakíthatjuk analóg jellé. A bemeneti és kimeneti mintavételezés nem szinkron történik, közöttük Tr időintervallum telik el. A Tr időintervallum egyrészt a konverziós időből, és a jelfeldolgozási időből tevődik össze. A mintavételes jelfeldolgozás folyamatábrája a következő ábrán látható. Tr elhanyagolható, ha sokkal kisebb, mint a beavatkozó szervek, érzékelők, és a folyamat időállandói. Ugyanilyen megfontolásból, 16 bites vagy nagyobb szóhosszúságú processzor és 10 bitesnél nagyobb felbontású A/D konverterek esetén, a diszkrét idejű jel a vizsgálatokhoz első közelítésben folytonos jelszintűnek tekinthető.
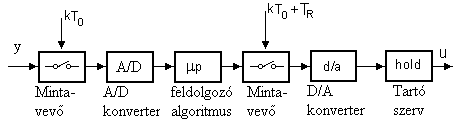
4. 2 ábra: Digitális jelfeldolgozás blokkvázlata.
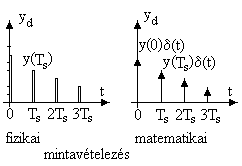
4.3. ábra: fizikai és matematikai mintavételezés
Az impulzusok szélessége a mintavételi lépésközhöz képest kicsi. Ezért nagyobb hiba nélkül helyettesíthetjük a mintavételezett impulzusokat azonos területű Dirac impulzusokkal. Ezáltal az idealizált matematikai mintavételezéshez jutunk, ami a mintavételes rendszerek tárgyalását lényegesen leegyszerűsíti. Figyelembe kell venni, hogy a mintavételezés információvesztést jelent, mivel csak a mintavételi pontokban ismert a jel értéke. Az y(t) és yd (t) jelek közötti kapcsolat nem kölcsönösen egyértelmű. Az információ vesztés csökken a mintavételi frekvencia növelésével.
A digitális szabályozók kimenete diszkrét idejű jel, amelyet folytonos idejűvé kell alakítani. Ezt a D/A átalakító végzi. E folyamat két részre osztható: dekódolásra és tartásra. A dekódolás folyamán a diszkrét idejű digitális jelből analóg impulzusok lesznek. Az analóg impulzus sorozatból a tartó áramkör folytonos idejű jelet állít elő. Többféle tartóáramkör lehetséges, attól függően, hogy a megelőző n darab diszkrét idejű értékből milyen extrapolációval történik a kimenő jel előállítása.
Zérusrendű tartó áramkör a legegyszerűbb. Az nTs és (n+1)Ts időpontok között ekkor y(nTs) állandó érték a kimenet.
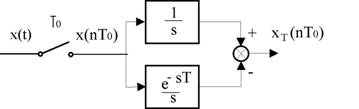
Ez lépcsős görbét jelent. A zérusrendű tartószerv átviteli függvénye:
![]()
Az első rendű tartó áramkör az nTs és (n+1)Ts időpontok között az y(nTs) és y((n-1)Ts) értékekből képez egyenest. A másodrendű tartók az extrapolációt parabola segítségével végzi. Gyakorlatban a zérusrendű tartónak a jelentősége a legnagyobb.
A mintavételezett jelek matematikai leírása
Az időtartományban a mintavételezett jeleket Dirac impulzusokból álló sorozatként ihatjuk le:
![]()
A mintavételezett jelek leírása a frekvencia tartományban a Laplace transzformáció segítségével lehetséges. A mintavételezett jelsorozat Laplace transzformáltja az eltolási tétel felhasználásával:
![]()
A ![]() jelölést bevezetve
kapjuk a diszkrét idejű jel z transzformáltját, vagy diszkrét Laplace
transzformáltját:
jelölést bevezetve
kapjuk a diszkrét idejű jel z transzformáltját, vagy diszkrét Laplace
transzformáltját:
![]()
A z változót késleltetési, vagy eltolási operátornak is tekinthetjük, ahol a z-k együtthatóval való szorzás azt jelzi, hányadik a jel a mintavételezett jelsorozatban. Ha egy jelsorozatot z-vel szorzunk, a művelet eredményeképpen a jelsorozat időben negatív irányban tolódik el. Ugyanígy, a z-1-el történő szorzás időben késleltetést jelent.
E felfogás szerint a transzformáció más megközelítéssel is bevezethető.
Egy x=x[k] diszkrét idejű jelsorozat X(z)=Z diszkrét idejű Laplace transzformáltja, más néven z transzformáltja a következő:
![]()
A z változó dimenzió nélküli mennyiség, vagy néha radián mértékegységben adják meg, mint a diszkrét idejű körfrekvenciát.
A jeleket belépő jeleknek tekintjük, azaz ![]() ha k < 0.
ha k < 0.
Az inverz z transzformációelvileg az inverziós integrállal hajtható végre:
![]()
k egész szám.
Az inverziós integrál kiértékelése azonban általában nehéz, így más módszereket használunk, hasonlóan az inverz Laplace transzformációhoz.
A z transzformáció tulajdonságai és az inverz z transzformációs módszerek
1.2. Az impulzusok és az egységugrás transzformáltjai.
A DI egységimpulzus z transzformáltja.
A diszkrét idejű egységimpulzus ([0] = 1, [k] = 0 egyébként) z transzformáltja a definicióból következik:
Z = 1. (9.)
Hasonlóan látható be, hogy:
Z = z-r (10.)
Ebből következik, hogy a véges hosszúságú belépő DI jel z transzformáltja a z-1 változó polinomja:
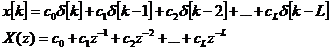 (11.)
(11.)
Ez kifejezhető a z két polinomjának hányadosaként:
![]() (12.)
(12.)
A DI egységugrás transzformáltja.
A definiciós képletbe helyettesítve:
![]() (13.)
(13.)
A mértani sor konverges, ha ![]() , azaz, ha
, azaz, ha ![]() A mértani sort másképpen felírva:
A mértani sort másképpen felírva:
![]() (14.)
(14.)
A Laplace transzformáció definiciójából következik, hogy az f[k]=1, vagy a g[k]=2-[k] DI jel transzformáltja megegyezik [k] transzformáltjával, vagyis F(z)=G(z)=z/(z-1).
Linearitás:
Mind a transzformáció, mind az inverz transzformáció lineáris:
![]() (15.)
(15.)
![]() (16.)
(16.)
Csillapítási tétel:
Bármely komplex q szám esetén:
![]() (17.)
(17.)
Ha q valós, és -1<q<+1, akkor az x szorzótényezője az időtartományban exponenciális csillapítást jelent. Innen kapta a tétel a nevét. Az igazolás egyszerű, nem részletezzük.
A tétel alkalmazásaként kapjuk:
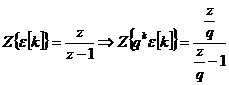 (18.)
(18.)
Gyakori előfordulása miatt érdemes megjegyezni:
![]()
Késleltetett belépő jel transzformáltja.
Ha X(z)=Z, akkor
![]() (20.)
(20.)
A tételt eltolási vagy késleltetési tételnek is nevezik.
Nem belépő jel késleltetése.
Ha X(z)=Z, akkor a késleltetett jel z transzformáltja:
![]() (21.)
(21.)
A késleltetett jel z transzformáltját X(z) nem határozza meg, mert annak számításakor az
x[-1], x[-2], értékeket nullának tekintettük, tehát ezeket külön-külön figyelembe kell vennünk. Ha ezek értéke nulla, akkor az egyenlet a (20.) formára egyszerűsödik.
Speciálisan r=1 és r=2 esetén:
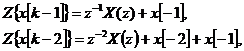 (22.)
(22.)
Siettetett DI jel
Ha X(z)=Z, akkor az egy ütemmel siettetett (hátratolt) jel transzformáltja:
![]() (23.)
(23.)
Az általánosítás több ütemre nem okoz nehézséget, itt nem foglalkozunk vele.
Belépő jelek konvolúciója:
A két belépő jel konvolúciójának z transzformáltja transzformáltjuk szorzata.
![]() (24.)
(24.)
Inverz z transzformáció
Az X(z) z transzformáltnak megfelelő diszkrét x[k] jelet az X(z) inverz z transzformáltjának nevezzük. Az inverz z transzformáltat különféle módszerekkel határozhatjuk meg:
Résztörtekre bontással és z transzformációs táblázat segítségével
Polinom osztással
Differencia egyenlet megoldásra visszavezetve
Komplex inverziós integrállal.
A módszerekre a következőkben mutatunk példákat.
Résztörtekre bontás módszere
A jel z tartománybeli alakját parciális törtek összegére bontjuk, és az így nyert résztörteket táblázatból kikeressük. Az eredmény az egyes tagok összege lesz.
A törtet
![]() ,
, 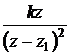 ,
, 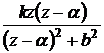 alakú résztörtekre
bontjuk, és azokat táblázat
alakú résztörtekre
bontjuk, és azokat táblázat
segítségével transzformáljuk az időtartományba.
Legyen
![]()
A parciális törtekre bontott alak:
![]()
az A és B együtthatókat meg kell határozni.
![]()
z=1 esetén B=5,
Z=0.4 értékkel pedig A=-2 adódik.
![]()
Táblázatból visszakeresve a diszkrét jelet:
![]()
![]()
![]()
Polinom osztás
A módszer akor használható, ha a jelek egyoldalúak, vagyis csak pozitív vagy csak negatív időpontokban fellépő jelek. Ha a z transzformáltat polinomok hányadosaként írjuk fel, csökkenő kitevőkkel. A két polinomot elosztva az eredményt z végtelen soraként kapjuk, és a z együtthatói adják a diszkrét x k impulzussorozat elemeit.
Példa:
![]()
Ezt át kell alakítani z -1 hatványai szerinti polinomok hányadosává:
![]()
Az osztás eredménye:
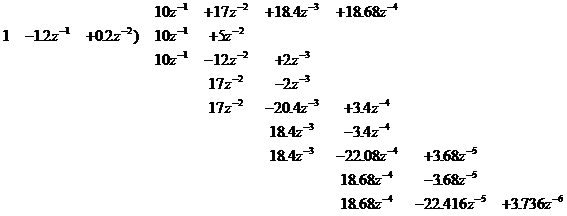
Az osztás eredménye:
![]()
Az ![]()
![]()
![]()
egyenlet alapján a diszkrét jelsorozat a következő:
x(0)=0
x(1)=10
x(2)=17
x(3)=18.4
x(4)=18.68
A módszerrel általában nem kapunk zárt formát az időfüggvényre. De a számítás tetszőleges pontosságig folytatható.
Osztással határozzuk meg a mintavételezett jelsorozatot:
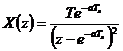
Ez átírható a következő formába:
![]()
Az osztás eredménye:
![]()
Ay eredmény zárt formában is felírható:
![]()
Inverz transzformáció differenciaegyenlet megoldással
A módszer előnye, hogy algoritmizálható. Legyen a z tartományban adott jel belépő függvény, és a következő egyenlettel adott:
![]()
![]() Írjuk fel az alábbi alakban:
Írjuk fel az alábbi alakban:
![]() ;
;
Ahol az u(z) gerjesztés a Dirac delta z transzformáltja, mivel ![]() .
.
Rendezzük át az egyenletet:
![]() ,
,
Majd alakítsuk át a kifejezést differencia egyenletté:
![]()
Mivel u[k] a diszkrét egység impulzus, u[k]=1, ha k=0, és u[k]=0, ka k?0.
Legyen k=-2. Ekkor az egyenlet:
![]()
A kezdeti értékek: x[-1]=x[-2]=0, mivel belépő jel, u[-1]=u[-2]=0, mivel egység impulzus.
Így a megoldás elsőtagja:
x[0]=0
Helyettesítsünk be k=-1-et.
![]()
A kezdeti értékek: x[0]=0, az előbb már ezt meghatároztuk, x[-1]=0, u[0]=1, u[-1]=0,
A második tag:
X[1]=10
Helyettesítsünk be k=0-t. A következő megoldandó differencia egyenlet:
![]()
A kezdeti feltételek: x[0]=0, x[1]=10, u[0]=1, u[1]=0.
A harmadik tag:
X[2]=17
Helyettesítsünk be k=1-t. A következő megoldandó differencia egyenlet:
![]()
A kezdeti feltételek: x[0]=0, x[1]=10,x[2]= 17, u[0]=1, u[1]=0.
A negyedik tag:
X[3]=18.4
A következő differencia egyenletekben az u[k] értékeire mindig 0-t kapunk. A számítások részletezésének mellőzésével az eredmények:
x[4]=18.68
x[5]=18.736
x[6]=18.742
x[7]=18. 7495
x[8]=18.7499…
Számításunk eredmény megegyezik a résztörtekre bontás és a polinomosztás módszerével kapott eredményekkel.
De ellenőrizhetjük számításainkat a kezdeti és a végérték tételekkel is:
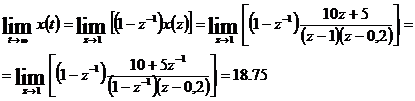
![]()
Oldjuk meg differencia egyenletté alakítással a következő visszatranszformálási feladatot is, amelynek végeredményét polinom osztással már közöltük. X(z) belépő függvény:
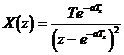
Alakítsuk át differencia egyenletté:
![]()
![]()
Legyen n=-2,
![]()
x[0]=0
Legyen n=-1,
![]()
x[1]=0
Legyen n=0,
![]()
![]()
Legyen n=1
![]()
![]()
![]()
Legyen n=2
![]()
![]()
![]() …
…
A mintavételezett jelsorozat:
![]() ,
, ![]() ,
, ![]() ,
, ![]() …, megegyezik az előbbi jelsorozattal, és zárt formában
megadható eredmény adódik.
…, megegyezik az előbbi jelsorozattal, és zárt formában
megadható eredmény adódik.
A folytonos idejű rendszerek diszkrét modellje
a diszkrét idejű szabályozót folytonos modellel helyettesítjük és folytonos idejű a szabályozott folyamat,
a diszkrét idejű szabályozóhoz diszkrét idejű folyamat modellt állítunk elő
A szabályozási kör vizsgálatakor célszerű a folytonos modell célszerűbb, mivel így a rendszer mintavételi pontok közötti viselkedése is megismerhető.
A folytonos és diszkrét idejű rendszerek közti összefüggést az s
és a z tartomány között a ![]() összefüggés írja le. Az
összefüggés az s sík képzetes tengelyét, (s=0) a z síkon egységsugarú körré képezi le, az alábbi ábra szerint.
összefüggés írja le. Az
összefüggés az s sík képzetes tengelyét, (s=0) a z síkon egységsugarú körré képezi le, az alábbi ábra szerint.
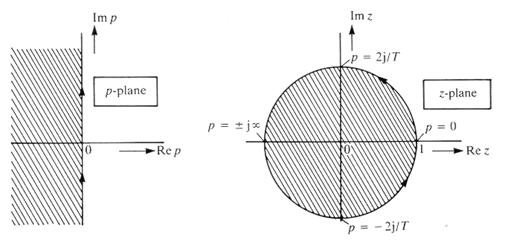
A konvertálásra számos módszer létezik, közülük néhányat a következő rész ismertet. A módszerek egy része az azonos bemenő jelek hatására adott azonos válaszon alapul. Mind a folytonos, mind a diszkrét rendszer kimenő jeleinek azonosaknak kell lenni a mintavételi pillanatokban. Ide tartoznak az egység ugrás és egység sebesség invariáns módszerek. A módszerek egy másik csoportja pedig a szimulációs módszerekből származik. Ilyen például a bilineáris közelítés, mely a trapéz módszerből származik, vagy a differencia egyenlet módszer.
Egység ugrás invariáns módszer, vagy zérusrendű tartó módszer. A módszer által eredményezett diszkrét és az eredeti folytonos rendszer egység ugrásra adott válasza megegyezik a mintavételi pillanatokban. A szabályozott szakasz elé zérusrendű tartó áramkört mögé, pedig egy mintavételező áramkört tételezünk fel, így az eredményül kapott rendszer bemenete és kimenete egyaránt digitális lesz. A zérusrendű tartót és a mintavételezőt is bevonjuk a konverzióba. A konverziós egyenlet:
![]()
az egyenletben a Z operátor a z transzformációt, L-1 pedig az inverz Laplace transzformációt jelenti. A módszert a szabályozott szakasz konvertálására használják. Nem megfelelő azonban a módszer a szabályozó diszkretizálására, mivel a zérusrendű tartó áramkör fázis késleltetést, valamint a frekvencia átvitelben torzítást okoz.
Egység sebesség invariáns módszer. Ha a bemeneti egységugrás jel helyett egység sebesség jelet használunk, az egység sebesség invariáns, vagy elsőrendű tartó módszerhez jutunk. A folytonos és a kapott diszkrét rendszer válasza ez esetben az egység sebesség jel esetén egyezik meg. A konverziós egyenlet a következő:
![]()
A módszer elfogadható eredményt ad folytonos idejű szabályozók konvertálása esetén is.
Impulzus válasz invariancián alapuló átalakítás
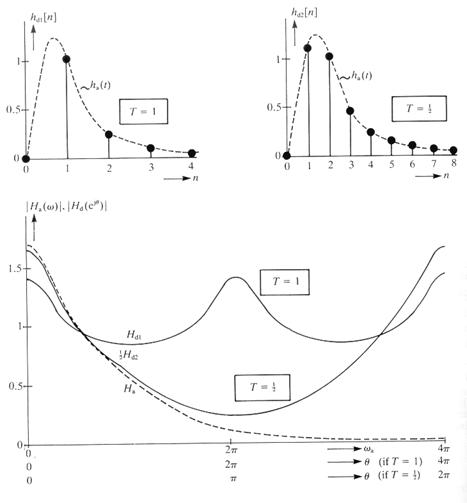
E módszer esetén az ismert analóg szűrő súlyfüggvényéből - impulzus válasz, ha(t) - és ennek frekvencia függvényéből – Ha(w - indulunk ki. Az IIR szűrő hd[n] impulzus válasza a mintavételi pontokban meg kell, hogy egyezzen a folytonos szűrő impulzus válasz függvényével:
![]()
T a diszkrét rendszer mintavételi periódusideje.
Az előzőek alapján felírható a diszkrét rendszer amplitúdó-frekvencia függvénye:
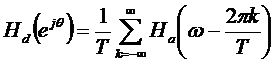
Ahol ![]()
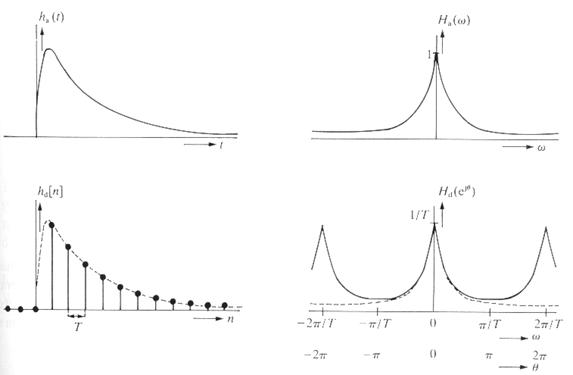
11. ábra: Impulzus válasz invariancián alapuló módszer
A módszer problémája, hogy alkalmazhatósága a T mintavételi idő nagyságától függ, a frekvencia függvénynél előforduló átlapolás miatt (aliasing jelenség). Azaz, az időtartományban meglévő hasonlóság a frekvencia tartományban nem áll fenn kis mintavételi frekvenciák esetén.
Példa: Legyen az analóg szűrő átviteli függvénye:
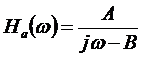
A Laplace transzformált:
![]()
A súlyfüggvény táblázatból meghatározható:
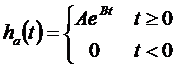
A diszkrét impulzus válasz:
![]()
A z transzformált pedig:
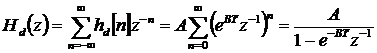
A rendszer blokkvázlata az alábbi:
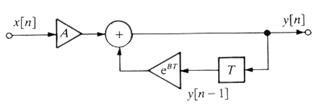
12. ábra: a szűrő blokkvázlata.
Hasonlítsuk össze az analóg és a diszkrét átviteli függvényt:
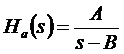
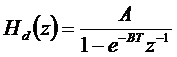
A Ha(s) függvénynek pólusa van
az s =B helyen, amíg a Hd(z) diszkrét rendszer
pólusa a ![]() helyen található.
helyen található.
Ez alapján megfogalmazható a tervezési módszer általános szabálya:
Az analóg
szűrő minden p=pk
pólusát át kell konvertálni a ![]() pólusokká.
pólusokká.
Általában az analóg szűrő az alábbi formában adott:
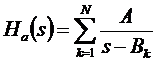
A tervezés során a diszkrét szűrőt az alábbi formában kapjuk:
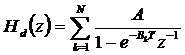
A stabil analóg szűrőből így konvertált diszkrét szűrő is stabil lesz minden esetben.
A differenciál egyenlet helyettesítése differencia egyenlettel
Az analóg szűrő az átviteli függvényével adott:
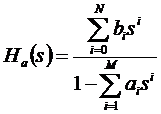
Ebből felírható a rendszer differenciál egyenlete:
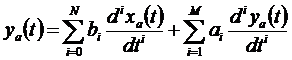
Ezután közelítjük a rendszert a differencia egyenletével:
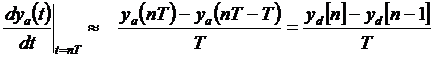
Az yd[n] a diszkrét szűrő kimeneti jele.
A módszert általánosíthatjuk is:
![]()
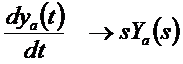
![]()
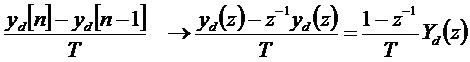
Így a diszkrét IIR szűrő átviteli függvénye az alábbi lesz:
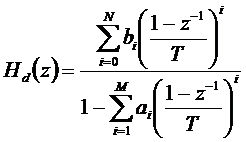
A módszer az s síkot a z síkra képezi le a 13. ábrának megfelelően. Az s sík origója ( s=0) megfelel a z sík 1 pontjának. Az s=j és s=-j pontok a z=0 pontba kerülnek. A7 s sík képzetes tengelye pedig megfelel a z síkon a 0.5 sugarú kör kerületének. Az s sík stabil régiója ( vonalkázott) a z síkon szintén stabil tartományba kerül, a kör belsejébe, tehát a diszkrét szűrő is stabil lesz, ha az analóg rendszer stabil volt.
A frekvencia tartománybeli viselkedés azonban nem lesz azonos. Ez akkor
lenne azonos, ha a vonalkázott s tartomány leképezése az egységsugarú kör
belsejére történne. Ehhez közel csak a kis frekvenciákhoz tartozó területekre
igaz, ahol ![]() . Tehát a közelítés
csak a mintavételi frekvenciánál jóval kisebb frekvenciákra lesz
megfelelő.
. Tehát a közelítés
csak a mintavételi frekvenciánál jóval kisebb frekvenciákra lesz
megfelelő.
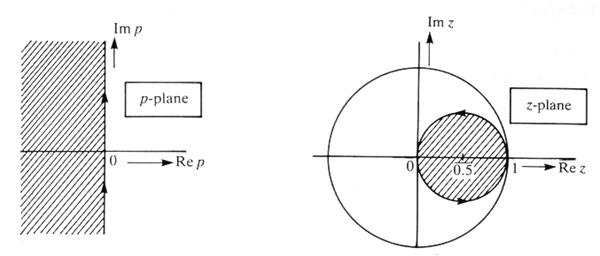
13. ábra: s z leképezés.
A derivált közelítésének bemutatott módszerét ”backward difference” módszernek nevezik:
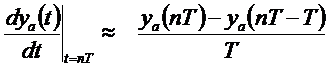
Egy másik lehetőség a „”forward difference” módszer:
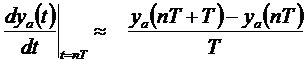
Ez alapján az s és z változók közötti összefüggés:
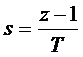 és
és ![]()
Ez esetben az s tartomány képzetes tengelye függőleges egyenesbe képződik le a z síkon, amint a 14. ábra mutatja. Ezért a frekvencia tartománybeli viselkedés ezúttal is csak kis frekvenciákon lesz hasonló.
E tulajdonsága miatt a módszert csak néhány speciális alkalmazás esetén használják, melyekre nem térünk ki ( pl. kapcsolt kapacitású szűrők).
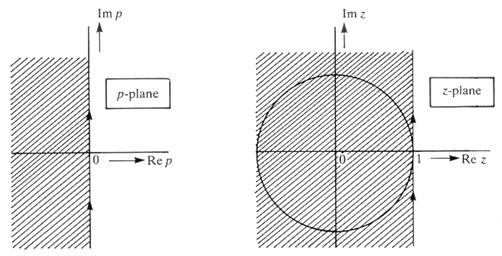
14. ábra: s-z leképezés z= 1+sT esetén.
Transzformáció bilineáris transzformációval
A leggyakrabban alkalmazott a folytonos szűrőt kiindulásként használó módszerek közül.
Az s-z leképezés az alábbi képlet szerint történik:
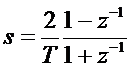 , illetve
, illetve
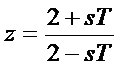
A leképezés a 15. ábra szerint történik.
A módszer az s sík képzetes tengelyét az egység sugarú kör kerületére képezi le, az s=0 pont a z=1 pontba kerül. Az s=+j és s=-j pontok egyaránt a z=-1 pontba képződnek le. Az s tartomány negatív valós része az egység sugarú kör belsejének felel meg. Ily módon mindig stabil diszkrét rendszert kapunk, ha a kiindulási analóg rendszer stabil.

15. ábra: s-z leképezés bilineáris transzformáció esetén.
Példa:
Legyen a folytonos rendszer átviteli függvénye:
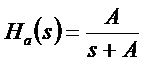
Írjuk fel a diszkrét rendszert a bilineáris transzformációval:
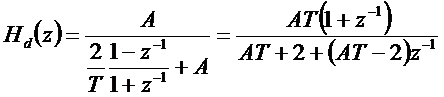
A frekvencia függvények A=1000 és T=0.001esetén a 16. ábrán láthatók.
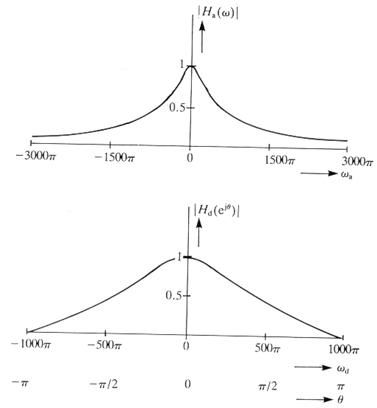
16. ábra: a bilineáris transzformációval kapott frekvencia függvények.
Az ábrán látható, hogy kétféle frekvencia szerepel: a, az analóg rendszer és d, a diszkrét rendszer frekvenciája.
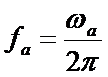
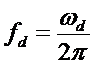 , illetve
, illetve 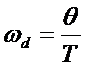
Egyik fő tulajdonsága a bilineáris leképezésnek, hogy az analóg
rendszer teljes frekvenciáját ![]() leképezi a diszkrét
rendszer alap intervallumára
leképezi a diszkrét
rendszer alap intervallumára ![]() .
.
Az a=0 pont megfelel a q pontnak, az a=+ pontot áttranszformálja a q p pontba, míg az a=- pontot a q p pontba képezi le.
Az analóg és diszkrétfrekvenciák között az alábbi összefüggés vezethető le:
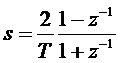
s=j és ![]() ,
, ![]() összefüggések figyelembe vételével:
összefüggések figyelembe vételével:
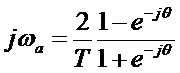

Azaz, a két frekvencia között az összefüggés nem lineáris, amint az a 17. ábrán látható. A jelenség a frekvencia „warping”, eltérés. Pozitív következménye, hogy a transzformáció sohasem okoz frekvencia átlapolást, az aliazing jelenség nem fordul elő. Viszont a tervezés folyamán a frekvencia karakterisztika specifikációjánál ezt figyelembe kell venni és a diszkrét szűrő frekvenciamenetét módosítani kell. E folyamatot ábrázolja a 18. ábra.
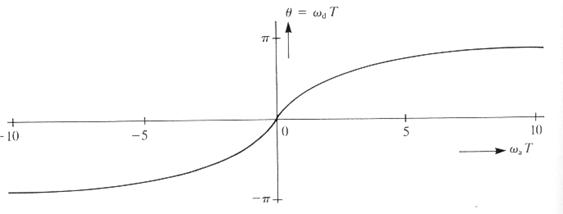
17. ábra: Az analóg és diszkrét frekvenciák közötti összefüggés bilineáris transzformáció esetén.
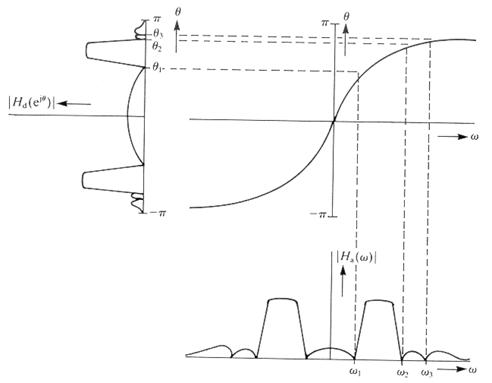
18. ábra: a frekvancia torzulás „warping” bilineáris transzformáció esetén.
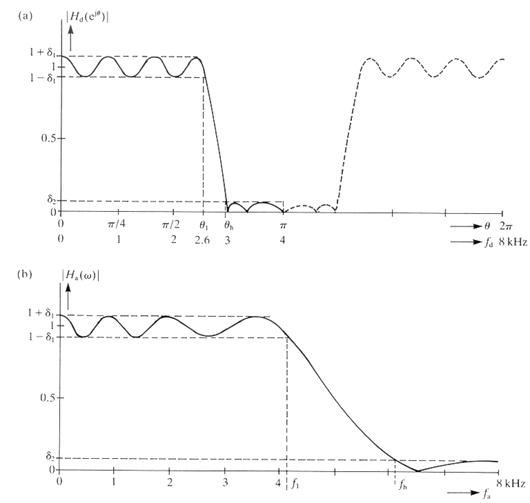
19. ábra: A diszkrét szűrő frekvencia karakterisztikája bilineáris transzformáció esetén.
Diszkrét idejű rendszerek átviteli függvénye
A diszkrét idejű átviteli függvény felírásához iduljunk ki egy egyszerű átviteli tagból, amely az n-ik kimeneti jelet két egymás utáni bemenő jelből, az n-ik és n-1-ik mitavételi értékből átlagolással állítja elő:
![]() .
.
Írjuk fel a z transzformáltat:
![]() .
.
A diszkrét idejű processzor átviteli függvényét kapjuk, ha a kimenő jel és a bemenő jel hányadosát képezzük:
![]()
Az átviteli függvényt átírva z pozitív hatványaival, a következő kifejezést kapjuk:
![]()
A W (z) átviteli függvény rendszerjellemző, megadja, hogyan állítja elő a diszkrét processzor a kimenő jelsorozatot a bemenő jelsorozatból. Ha adott az átviteli függvény, a bemenő jelsorozatból előállítható a kimenő jelsorozat:
![]()
Ha a bemenő jel a mintavételezett egység impulzus, d[n], a kimenet az egység impulzus válasz függvény, h[n] lesz. A z transzformáltakkal:
![]()
Egy lineáris diszkrét idejű processzor átviteli függvénye egyenlő a mintavételezett egység impulzusra adott válasz függvénnyel.
Az átviteli függvényről anyag a CD mellékletben található.
Diszkrét idejű tagok frekvencia átviteli függvénye
A diszkrét idejű tag frekvencia
átviteli függvényét az impulzus átviteli függvényből ![]() helyettesítés útján kapjuk. Sajnos, wd(j)
transzcendes függvény, ezért a frekvencia diagram komplikált, az aszimptotikus
közelítés nem alkalmazható. Felírható a mintavételezett jel spektruma.
helyettesítés útján kapjuk. Sajnos, wd(j)
transzcendes függvény, ezért a frekvencia diagram komplikált, az aszimptotikus
közelítés nem alkalmazható. Felírható a mintavételezett jel spektruma.
A spektrum meghatározásához a mintavételezett jelet az alábbi formában írjuk fel:
![]()
Az yd(jw) frekvencia spektrum ebből a következő alakú lesz:
![]()
A képletben ![]() a mintavételi
körfrekvencia, y(0) a jel értéke a t=0 időpontban. Az eredeti spektrum
a mintavételi
körfrekvencia, y(0) a jel értéke a t=0 időpontban. Az eredeti spektrum ![]() szeresére változik, és
a
szeresére változik, és
a ![]() frekvenciák körül periodikusan ismétlődik.
frekvenciák körül periodikusan ismétlődik.
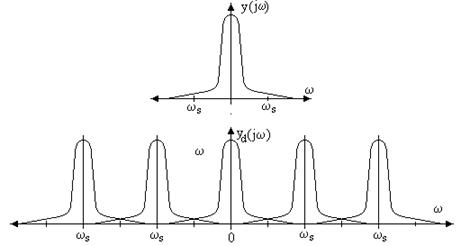
4. ábra: a mintavételezett jel spektruma.
A visszaállított jel spektruma ( Shannon tétel).
Minél kisebbek a jel nagyfrekvenciás
összetevői és nagyobb a mintavételi frekvencia, a jel helyreállítása annál
jobb lesz. Ha y(jw) spektruma a ![]() határok közé
esne, megfelelően nagy mintavételi frekvencia esetén a jel tökéletesen
helyreállítható lenne. A szükséges mintavételi frekvenciára vonatkoznak a
Shannon féle mintavételezési tételek.
határok közé
esne, megfelelően nagy mintavételi frekvencia esetén a jel tökéletesen
helyreállítható lenne. A szükséges mintavételi frekvenciára vonatkoznak a
Shannon féle mintavételezési tételek.
A mintavételi frekvenciának a jel wh határfrekvenciájának kétszeresénél nagyobbra kell választani.
A jelet olyan aluláteresztő szűrővel lehet helyreállítani, amely az w<wh tartományban Ts szeres erősítéssel viszi át a jelet, e frekvenciák felett pedig vág.
A Shannon tételek tájékoztatást adnak a mintavételi frekvencia minimális értékére, de csak elméleti határeseteket fogalmaznak meg. A valóságban a jelek végtelen sok felharmonikust tartalmaznak. Emellett a kimeneti aluláteresztő szűrők karakterisztikája sem ideális. Ezen okok miatt mintavételezés miatt mindig keletkezik hiba. A digitális jelfeldolgozó rendszerek ára nagymértékben függ a megvalósítandó mintavételi frekvenciától, az mindig az ár és a megengedett információ vesztés közötti kompromisszum eredménye. A mintavételi frekvencia csökkenthető, ha a bemenő jel frekvenciáját korlátozzuk. Ezért a bemeneten is alkalmaznak aluláteresztő szűrőt, amely a feldolgozás szempontjából érdektelen frekvenciákat kiszűri.
A folytonos rendszerek stabilitásának a feltétele volt, hogy a zárt
rendszer pólusai a komplex síkon a jw
tengelytől balra helyezkedjenek el. A folytonos rendszerek stabilitására
vonatkozó, a rendszer pólusaira vonatkozó definíciók diszkrét rendszerekre is
érvényesek. Ezt a feltételt kell átalakítani a z tartománynak megfelelően.
Ehhez a ![]() összefüggés szerint kell az s sík pontjait a z síkra
leképezni. Ha az s síkon kiindulunk a képzetes tengely mentén a jw=0 pontból a pontba pontba, a z síkon egy teljes
egységsugarú kört írunk le, az óramutató járásával ellentétesen. A jw
tengelytől balra eső pontok az egység sugarú kör belsejébe kerülnek.
Vagyis, a diszkrét idejű rendszerek stabilak, ha összes pólusuk az
egységsugarú körön belül fekszik.
összefüggés szerint kell az s sík pontjait a z síkra
leképezni. Ha az s síkon kiindulunk a képzetes tengely mentén a jw=0 pontból a pontba pontba, a z síkon egy teljes
egységsugarú kört írunk le, az óramutató járásával ellentétesen. A jw
tengelytől balra eső pontok az egység sugarú kör belsejébe kerülnek.
Vagyis, a diszkrét idejű rendszerek stabilak, ha összes pólusuk az
egységsugarú körön belül fekszik.
Általános esetben a diszkrét rendszer átviteli függvénye tört, melynek számlálója m-ed fokú, nevezője pedig n-ed fokú polinom:
![]() .
.
A karakterisztikus egyenlet, D(z) gyökei meghatározzák a rendszer tranziens viselkedését.
Ha a bemenő jel egységimpulzus, és a kezdeti értékek zérussal egyenlők, a kimenő jel, azaz a rendszer egység impulzusra adott válasz függvénye megegyezik az átmeneti függvénnyel, amint ezt már korábban leírtuk:
![]()
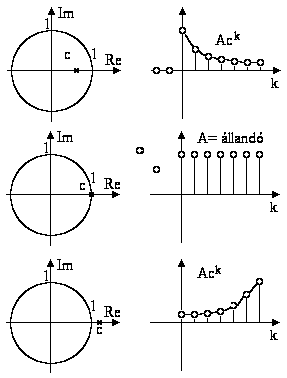
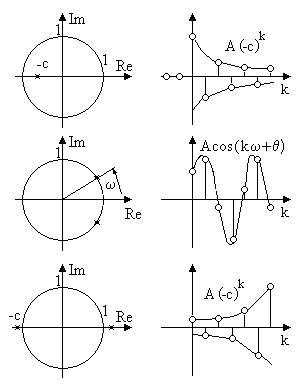
A diszkrét idejű rendszer stabil, ha az impulzus válasz aszimptotikusan zérushoz tart. Az alábbi ábra a különböző gyökökhöz tartozó válaszfüggvényeket foglalja össze.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2339
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved