| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Rozwiązanie I metodą.
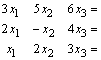
![]()
![]()
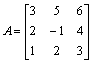
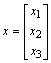
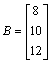

Jeseli ![]()
![]()
![]()

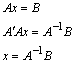 Wzory
Krammera
Wzory
Krammera
Rozwiązanie II metodą.
![]() gdzie W = wyznacznik macierzy współczynników
gdzie W = wyznacznik macierzy współczynników
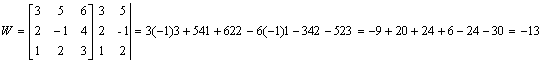
![]() w miejsce Xi ma kolumnę wyrazów
wolnych ???????
w miejsce Xi ma kolumnę wyrazów
wolnych ???????
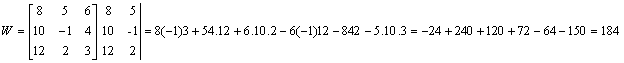
![]()
Rozwiązanie III metodą.
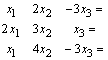
![]()

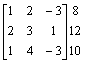
macierz wektor
współczyn prawo
ników stronny
przekształcamy lewą stronę do macierzy jednostkowej:
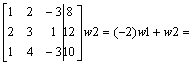
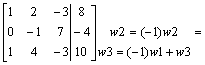
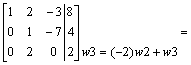
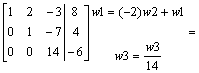
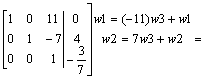
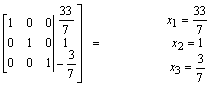
Przykład: Oblicz wskaźnik macierzy IV stopnia

![]()
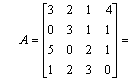
Wszystkie kolumny i rzędy mają taką sama ilość zer. Mosemy więc wybrać dowolny element od którego rozpoczniemy obliczenia. Rozpoczniemy od zera z 3 rządu , 2 kolumny. Rząd 3, kolumna 2 zostają więc wyeliminowany z obliczeń.
![]()
![]()
![]()
![]()
![]()


![]()
![]()
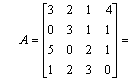
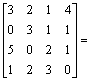
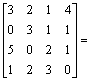
![]()
![]()
![]()
![]()
![]()
![]()
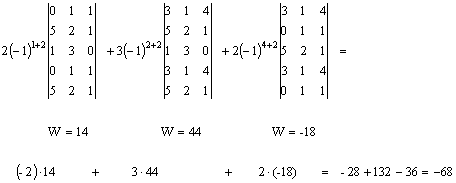
Przykład: Obliczyć macierz odwrotna metodą dopełnień.
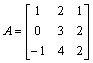
Obliczamy wskaźnik macierzy:
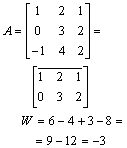
Obliczamy macierz dopełnień.
![]() Krok
1
Krok
1
![]()
![]()
![]()
![]()
![]() A=
A=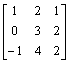 A=
A= 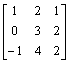 A=
A= 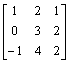
![]()
![]()
![]()
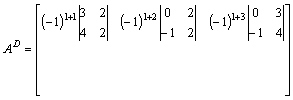
![]() Krok
2)
Krok
2)![]()
![]()
![]()
![]()
![]() A=
A= 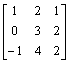 A=
A= 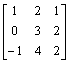 A=
A= 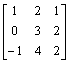
![]()
![]()
![]()
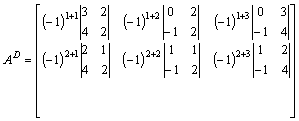
![]()
![]()
![]() Krok
3)
Krok
3)
![]()
![]()
![]() A=
A= 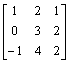 A=
A= 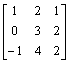 A=
A= 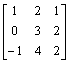
![]()
![]()
![]()
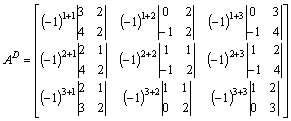
Krok 4) Obliczamy wskaźniki w macierzy dopełnień:

Krok 5) Obliczamy
elementy macierzy dopełnień według wzoru: ![]()
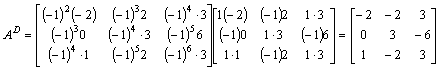
3) Transponujemy macierz dopełnień:
. 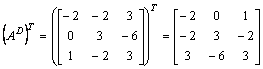
Obliczamy macierz odwrotną:
![]()
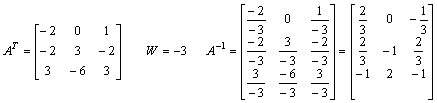
Dokonujemy sprawdzenia poprawności obliczeń.
Wykorzystujemy zalesność:
Macierz pomnosona przez macierz odwrotną daje w wyniku macierz jednostkową.
![]()
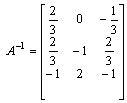
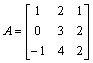
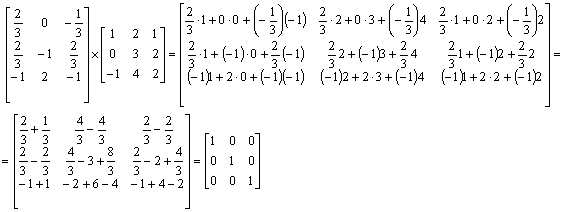
Mnosenie ![]() sprawdziło
się. Obliczenie macierzy pierwotnej zostało przeprowadzone poprawnie.
sprawdziło
się. Obliczenie macierzy pierwotnej zostało przeprowadzone poprawnie.
Przeprowadzimy to samo obliczenie wykorzystując metodę przekształceń elementarnych.
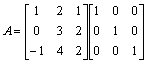
Polega ona na tym, se do macierzy dopisujemy jej postać jednostkową a następnie obie macierze poddajemy kolejnym przekształceniom ich elementów tak, aby postać macierzy sprowadzić do postaci macierzy jednostkowej. Po takich przekształceniach dopisana na początku macierz jednostkowa będzie miała postać poszukiwanej macierzy pierwotnej.
![]() Pierwszy
i drugi wiersz przepisujemy bez zmian bo jest jedynka i zero
Pierwszy
i drugi wiersz przepisujemy bez zmian bo jest jedynka i zero
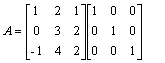
Aby zamiast elementu a 31 = -1 otrzymać 0 nalesy do wiersz 3 dodać wiersz 1.
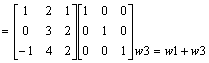 ok.!
ok.!
![]()
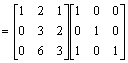
Aby zamiast elementu a 22 = 3 otrzymać 1 nalesy wiersz 2 podzielić przez 3
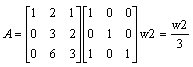 ok.!
ok.!
![]()
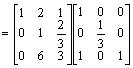
Aby zamiast elementu a 12 = 2 otrzymać 1 nalesy wiersz 2 pomnosyć przez (-2) i dodać do wiersza 1.
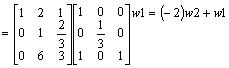 ok.!
ok.!
![]()
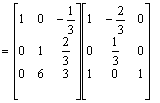
Aby zamiast elementu a 31 = -1 otrzymać 0 nalesy pomnosyć przez (-6) i dodać do wiersza 3.
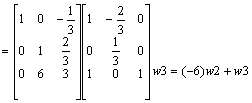 ok.!
ok.!
![]()
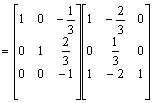
Aby zamiast elementu a 33 = -1 otrzymać 1 nalesy w3 pomnosyć przez (-1)
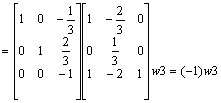 ok.!
ok.!
![]()
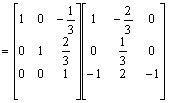
Aby zamiast elementu a 13 = -1/3 otrzymać 0 nalesy wiersz 3 pomnosyć przez (1/3) i dodać do w1
![]()
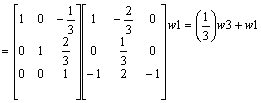 ok.!
ok.!
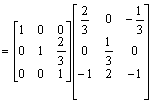
Aby zamiast elementu a 23 = 2/3 otrzymać 0 nalesy wiersz 3 pomnosyć przez (-2/3) i dodać do w2
![]()
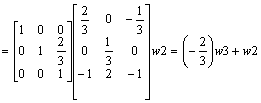 ok.!
ok.!
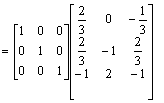
Przykład: Rozwiązać układ równań.
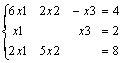
Tworzymy macierz współczynników i macierz wartości:
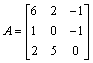
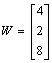
Obliczamy metodą przekształceń elementarnych.
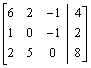
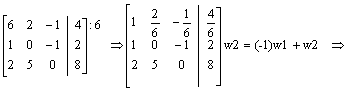
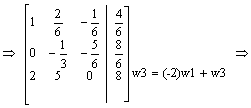
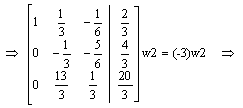
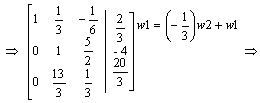
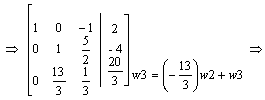
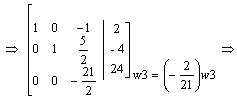
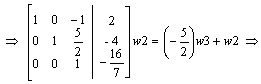
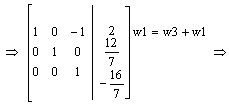
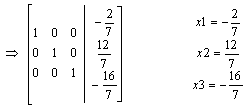
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1292
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved