| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
| Elektrik |
DOCUMENTE SIMILARE |
|
ÜLETÜM HATLARININ UZUNLUKLARINA GRE SINIFLANDIRILMASI
Enerji iletim hatlarü uzunluklarüna gre e ayrülabilirler. 0-100 kmye kadar olan hatlar küsa hatlar olarak adlandürülürlar. 100-250 km arasü olan hatlar ise orta uzunluktaki hatlar olarak adlandürülürlar. 250 km ve daha uzun hatlar ise uzun iletim hatlarü olarak adlandürülüp gerekli hesaplama yntemleri ile hat parametreleri bulunur.
Ületim hatlarünü elektriksel ynden inceleyecek olursak , hat parametreleri ve uzunluklar sz konusu olmaktadür. Üncelemelerimiz genellikle alternatif aküm kullanülan iletim hatlarü olduğundan alternatif akümda kullanülan tm byklkler burada sz konusu olacaktür.
Ületim hatlarünün bir omik direnci (R) vardür. Bu diren doğru akümdakine oranla deri olayü sebebiyle yaklasük 1,5 katü daha fazladür. Diğer taraftan komsu iletkenlerden akan akümlarün halkaladüğü akülar nedeniyle , faz iletkenlerinin self (z) ve karsülüklü (ortak) endktanslarü meydana gelmektedir. Sinzoidal akümlarla alüsüldüğündan endktans deyimi yerine sebeke frekansünün bir fonksiyonu olan endktif reaktans kullanülür. Hattün omik direnci ve endktif reaktansü birbirlerine seri bağlü olarak dsnlr ve hattün karakterize edilmesi iin bu iki byklğn seri toplamü empedans kullanülür.
te yandan yalütkan ortam (hava) iinde bulunan hatlarünün birbirlerine veya toprağa gre kaak kapasiteleri bulunacaktür. Sinzoidal bir gerilimle alüsüldüğü iin , frekansün bir fonksiyonu olan kapasitif reaktans deyimi kullanülür. Ancak hesaplarda tutulan genel yol , kapasitif reaktans yerine , bunun tersine esit olan sseptans ile alüsülmaktadür. Ületkenlerin toprağa karsü olan kaak direnleri ok kk olduğu iin oğunlukla ihmal edilir. Bu bakümdan hattün kapasitesi , hat ile toprak arasüna bağlanmüs sseptans ile , daha genel anlamda ise admitans ile temsil edilir. Sekil 1.de grlen devre bir iletim hattünün faz-toprak arasü esdeğer devresini gstermektedir. Burada ;
L: birim uzunluk basüna hattün faz-toprak endktans değeri
R: birim uzunluk basüna hattün direnci
C: birim uzunluk basüna hattün faz-toprak kapasitesi
R′: birim uzunluk basüna hattün
faz-toprak kaak direnci olarak tanümlanmüstür.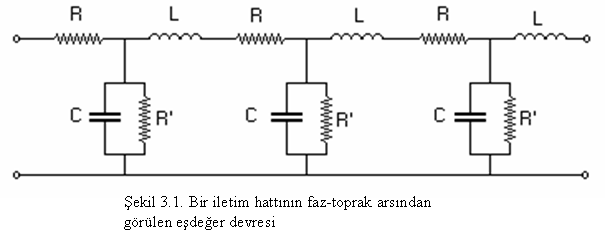 
Üslemlerde kullanacağümüz hat parametrelerinin girise ait olanlarü 1 indisi ile , üküsa ait olanlarü ise 2 indisiyle gstereceğiz. Asağüda bu parametreler ve aüklamalarü verilmistir.
Bir enerji iletim hattüna iliskin iki kapülü devre gsterimi Sekil 2.de gsterilmistir.
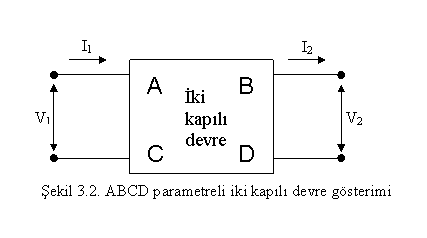
Sekilde grlen giris ve üküslar
arsündaki bağüntülar V1=AV2 +BI2 ve I1=CV2+DI2 . Bu esitlikleri matrissel formda
asağüdaki gibi yazabiliriz.
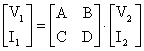elde edilir.
Buradaki A , B , C , D sabitlerine iletim hatlarünün genel devre sabitleri denir. Bunlar genel olarak kompleks sayülardür. Hattün herhangi bir ucundan baküldüğünda hat aynü , yani drt ulu devre simetrik ise A ve D birbirlerine esit ve birimsizdir. B ve C nin birimleri sürasüyla (ohm) ve S (Siemens = 1/ ) dur. Bu simetriliğin sağlanmasü kosuluyla
AD - BC = 1 dür ve sistem dengelidir.
1. Küsa Uzunluktaki Hatlar
Normal yapüda ve boylarü 0-100 km arasünda değisen hatlar iin kapasite ihmal edilebilir. Kapasitenin ihmal edilerek aküm ve gerilim denklemlerinin kurulabileceği iletim hatlarüna küsa iletim hatlarü denilir. Sekil de bir küsa iletim hattü genel gsterimi yer almaktadür. Grleceği gibi hattün kapasitesi ihmal edilmistir ve hat seri bir empedansla ifade edilmistir.
Bu empedansün değeri ; Z=R + jX = zℓ= rℓ + jxℓ dur. Burada ;
Z : Hattün faz basüna ohm olarak seri empedansünü
z : Hattün birim uzunlukta ve faz basüna ohm olarak seri empedansünü
X : Hattün faz basüna ohm olarak toplam endktif reaktansü
x : Hattün birim uzunlukta ve faz basüna ohm olarak endktif reaktansü
: Hattün uzunluğunu gstermektedir.
Küsa iletim hattü esdeğer devresi basit bir AC devresi olarak zlr. Devrede snt kollar olmadüğü iin hat basü ve hat sonu akümlarü bir birine esittir.
V1=V2 + ∆V=V2+Z I2 I1 I2
Bu ifadeleri matris seklinde yazarsak ;
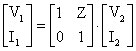
seklinde elde edilir. Burada A=D=1 , B=Z ve C=0 1/ . Yazülan bu ifadelere gre küsa iletim hattünün yk durumuna gre fazr diyagramlarü Sekil 4. ve Sekil 5.deki gibi olur.
2. Üki Adet Drt Ulu Devrenin Seri Bağlanmasü
Hat sabitleri A1 , B1 , C1 , D1 ve A2 , B2 , C2 , D2 olan iki adet küsa hat seri olarak bağlandüğü durumda ortak ABCD katsayülarünü bulalüm.
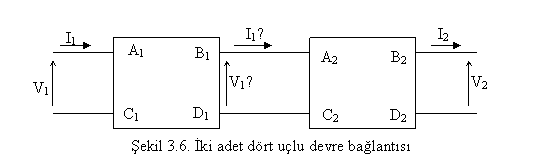
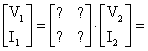? Matris islemini
yapabilmek iin ncelikle her iki devrenin aküm ve gerilim
bağüntülarünü yazalüm. Birinci hat iin;
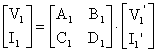
ve 2. hat iin ;
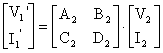olur. 1. hat iin
yazdüğümüz matriste 
matrisinin
bulunan değerini yerine yazacak olursak;
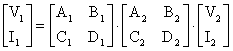matris
islemini yapacak olursak ;
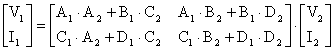bulunur. Burada ABCD
katsayülarü
sürasüyla; A =A1A2+B1C2 , B=A1B2 +B1 D2 , C=C1A2+D1C2 ve D=C1B2+D1D2 olur.
rnek 1.
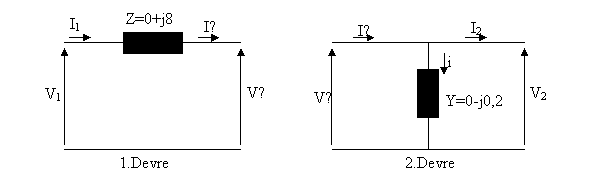
zm:
Sekil de grlen devreler birbirlerine seri olarak bağlandüklaründa A , B , C , D hat sabitlerini bulalüm. Seri bağlü iki devrenin sekli Sekil 6. daki gibi olur.
Birinci devreyi matrissel formda yazarsak ;
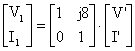(1)
aynü sekilde ikinci devre iinde matris ifadesini yazacak olursak ;
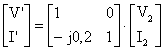(2)
elde edilir. 2 nolu
denklemi 1 de yerine koy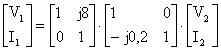arsak; 
bulunur. Bu
islemi yaparsak;
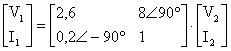seklinde buluruz. Burada ;
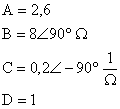
esit olur.
3. Üki Adet Drt Ulu Devrenin Paralel Bağlanmasü
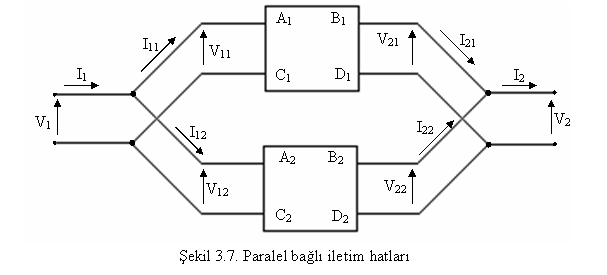
Sekilden V1=V11=V12 (1) , V2=V21=V22 (2) ve I1=I11+I12 (3) , I2=I21+I22 (4) yazülabilir. Birinci drt ulu devrede
V11=A1V21+B1 I21 (5) ve I11=C1 V21+D1 I21 (6) yazülabilir.
Ükinci drt ulu devrede ise
V12=A2 V22+B2 I22 (7) ve I12=C2 V22+D2 I22 (8) yazülabilir.
5 nolu denklemi B2 ile , 7 nolu denklemi ise B1 ile arpüp taraf tarafa toplayalüm.
Burada V11=V12=V1 , V21=V22=V2 ve I21+I22=I2 yerlerine yazarsak;
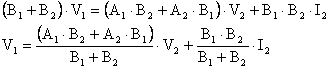
bulunur. Burada 
genel denklemine gre
ve 
olur.
V11=V12 esitliğini yazacak olursak ( 1 nolu denklem);
olur. Burada
I22 yi 4 nolu denklemden ekersek I2=I21+I22 ise I22=I2-I21
olur. I22yi V11=V12 esitliğinde
yerine koyalüm
seklinde yazülabilir. Bulduğumuz bu I21 değerini 6 nolu denklemde yerine yazalüm.
Tekrar V11=V12 esitliğini yazalüm.
Bu kez I21i
yerine koyalüm. I2=I21+I22 den I21=I2-I22 bulunur.
Bunu yerine koyarsak
bulunur. Bulunan bu I22 denklemini 8 nolu denklemde yerine koyalüm
I12=C2 V22+D2 I22
seklinde bulunur.
I1=I11+I12de bulunan denklemleri yerlerine yazarsak
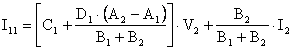
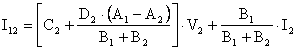
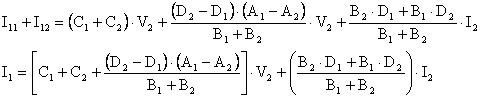
bulunur. Bu denklemi I1=CV2+DI2 genel ifadesine benzetecek olursak.
ve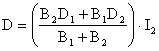 
seklinde yazabiliriz.
Yazdüğümüz bu ifadeleri matris seklinde asağüdaki gibi dzenleyebiliriz.
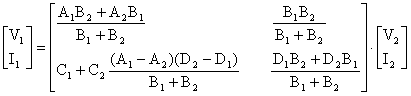
rnek 2.
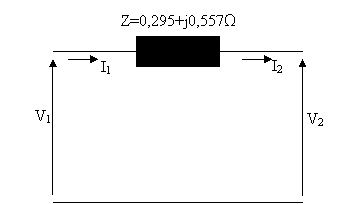
20 km uzunluğunda fazlü küsa bir iletin hattünün elektriksel hat sabitleri r = 0,295 /km , x = j0,557 /km ve hat sonu fazlar arasü gerilimU2 = 30 kV , hat sonu toplam g S2 = 8 MVA , ve cosφ = 0,9 (geri) olarak veriliyor. Hat basü gerilim , akümünü hesaplayünüz.
zm:
Hat küsa bir
hat olduğundan I1 I2 ve V1=V2+I2Z
seklinde yazabiliriz. V1 bulmak iin formlde I2 ve
Z değerlerinin hesaplanmasü gerekir. I2 iin 
ve Z iin ;
Z = ℓ(r+jx)=20(0,295+j0,557)=
5,9+j11,14 
cosφ = 0,9 geri ise bu aküm gerilime gre φ2= -25,83 geri anlamüna gelir. Bu sekilde;
seklinde yazülür.
Simdi V1 i hesaplayabiliriz;
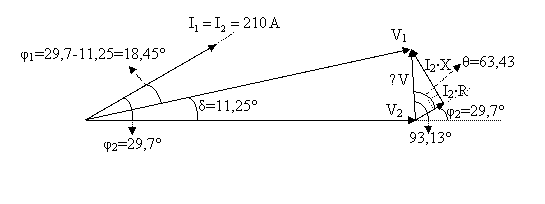
Bulunan bu değerleri fazr diyagramda asağüdaki
gibi gsterilir.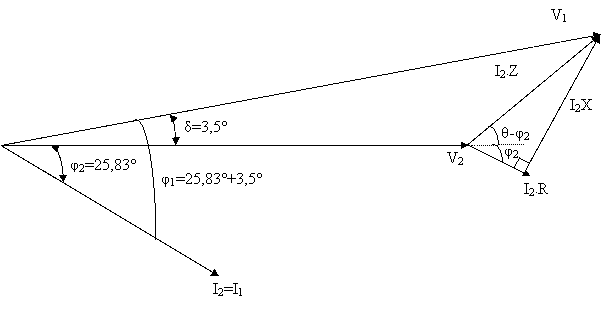 
rnek
Hat sonu gerilimi 66 kV olan ℓ=80 km uzunluğundaki bir hattün r = 0,20 /km ve x = 0,40 /km olarak veriliyor.
a) P2 = 21 MW , Q2 = 0 MVAr
b) P2 = 21 MW ve Q2 = 12 MVAr
c) P2 = 21MW ve Q2 = -12 MVAr olmasü durumlaründa hat basü parametrelerini bulunuz.
zm:
a) Omik ykte:
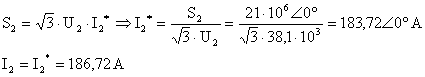
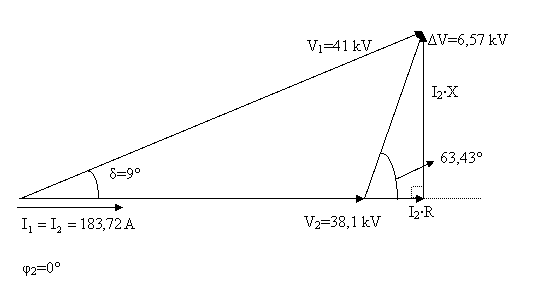
b) Endktif ykte:
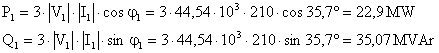
c)Kapasitif ykte:
4. Orta Uzunluktaki Ületim
Hatlarü
Uzunluklarü 100-250 km arasünda değisen hatlar orta uzunluktaki iletim hatlarü olarak tanümlanürlar.
Genellikle, tamamen kapasite olan snt admitans orta uzunluktaki hatlarün hesaplanmasünda dikkate alünür.
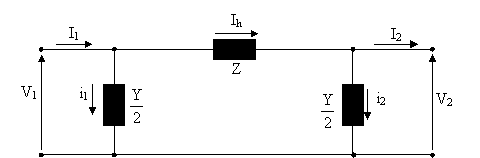
Sekil 8. Orta uzunluktaki hattün esdeğer devresi
Bu tr hatlarün zlmesinde ve T esdeğer devrelerinden yararlanülür. Hattün snt admitansü hattün bas ve sonlaründa iki esit paraya blnerek yerlestirilirse , elde edilen devreye nominal devresi ; hattün toplam snt admitansü hattün ortasüna , seri empedans da esit iki paraya blnerek bu snt admitansün sağüna ve soluna yerlestirildiğinde elde edilen devreye T devresi denilir.
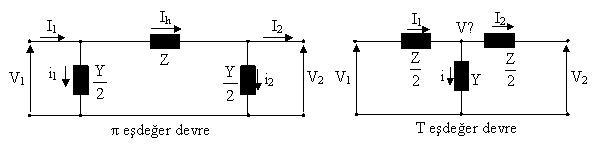
Sekil 9. π ve T esdeğer devreleri
4.1.Nominal devresi
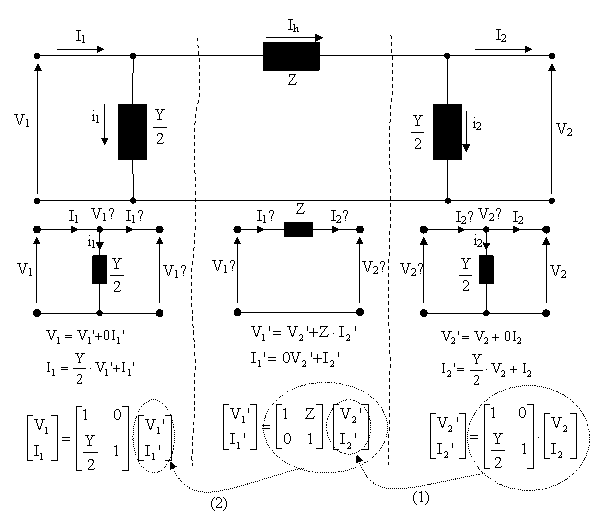
Sekil 10. π esdeğer devre parametrelerinin bulunmasü
Nominal devresi esitliklerini Sekil 10.dan ükaralüm. nce (1) nolu islemi yapalüm;
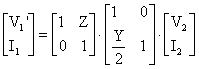bulunan bu matrisi 
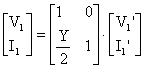de yerine
yerine koyalüm.(2) nolu islem.
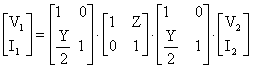seklinde bulunur. Burada katsayülar;
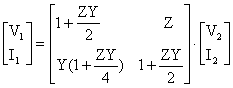
Esdeğer Devrenin Klasik Yntemle
zlmesi
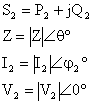
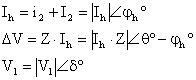
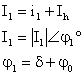
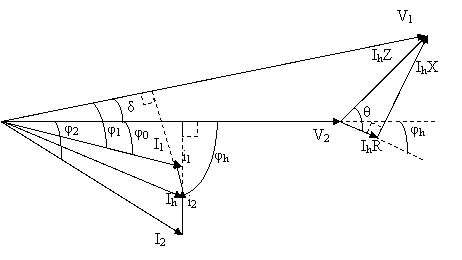
Sekil 11. π esdeğer devre fazr diyagramü
4.2. Nominal T devresi
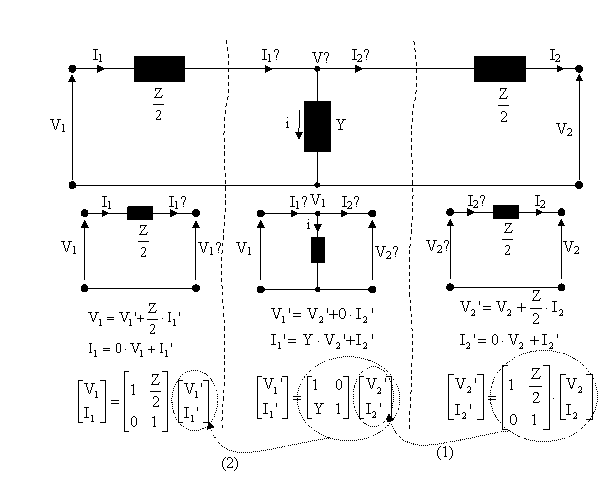
Sekil 12. T esdeğer devre parametrelerinin ükarülmasü
T esdeğer devrenin ABCD parametrelerini bulmak iin Sekil 12.de nce (1) nolu islemi yapalüm;
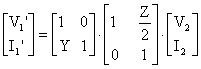bulunan matrisini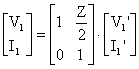
de
yerine koyarsak ( 2 nolu islem);
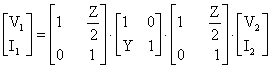elde edilir.
Bu islemi yapacak olursak;
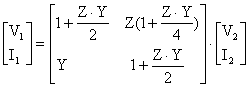matrisi elde edilir. Buradan ABCD katsayülarü;
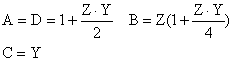
olur.
4.2.1. T devresinin klasik yntemle zlmesi
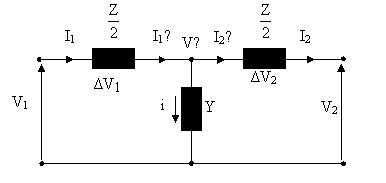
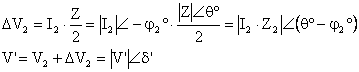
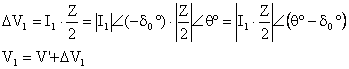
rnek 4.
180 km uzunluğundaki bir iletim hattünün sonundaki gerilim 154 kV olup sabittir. Hat sonunda 80 MW ve 45 MVAr değerinde aktif ve reaktif gler ekilmektedir. Hattün birim uzunluk basüna empedans ve reaktans değerleri r = 0,12 /km ve x = j0,41 /kmdir. Hattün kapasitansündan dolayü olusan admitans değeri ise 2,7810-6 S/km dür. Bu hattün ve T esdeğer devrelerini kullanarak hat basü isletme kosullarünü bulunuz.
a) T esdeğer devreyi kullanarak zm:
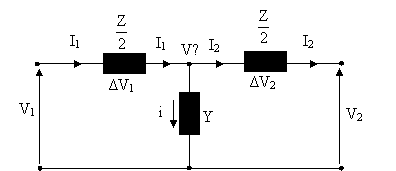
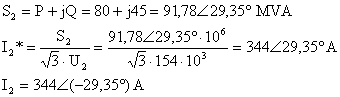
T
esdeğer devrede V1 gerilimini
ifadesinden
bulabiliriz.
Bunun iin I1 ve V′ değerlerinin bulunmasüna
ihtiya vardür.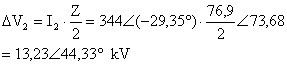 
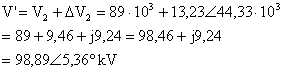
I1 değeri ise I1 =I2+i
den bulunur. Burada nce i değerini bulmamüz gerekmektedir. 
V1
değerini hesaplarsak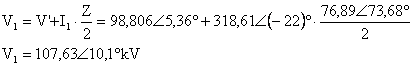 
bulunur.
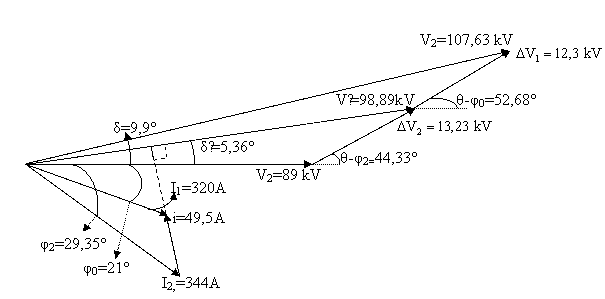
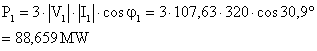
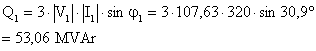
Problemi hat sabitleri ile zelim.
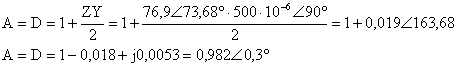
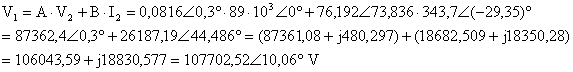
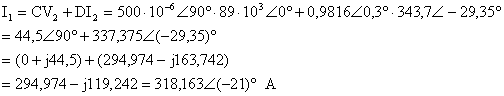
grldğ her iki yntem kullanülarak aynü sonulara ulasmak mmkndr.
b) esdeğer devre ile zm:
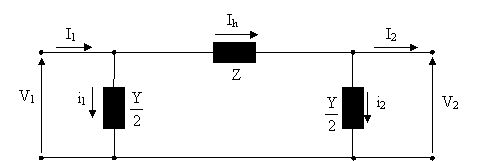
V1 =V2+Z.Ih ve Ih =I2+i2 dür. Yani V1 i hesaplamak iin Ih değerini hesaplamamüz gerekmektedir. Bunun iinde i2 değerinin hesaplanmasüna ihtiya vardür.
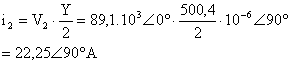
I1 değeri ise i1 ve Ihün toplamüna esittir.
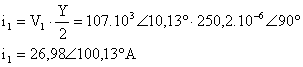
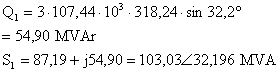
Hat parametreleri ile zm:
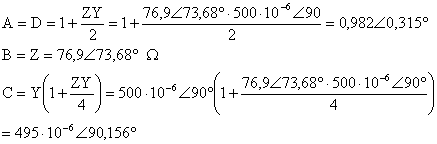
5. Uzun Ületim Hatlarü
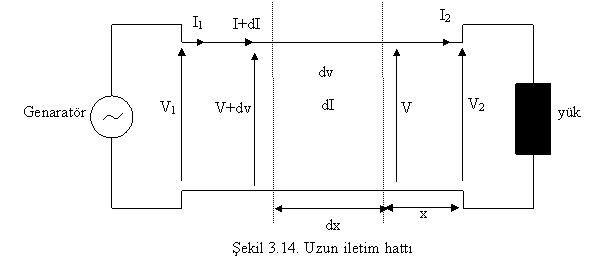
250 km den byk iletim hatlarünün kesin zm ve hesaplamalarün tamamen doğru yapülabilmesi iin hat sabitlerinin gerekte olduğu gibi hat boyunca niform dağülmüs olduğu dsnlmelidir.
fazlü bir hattün tek faz ve ntr bağlantüsü yukarüda grlmektedir. Hattün zm iin empedans ve admitansün esit dağülmüs olduğu dsnldğnden toplu parametreler gsterilmemistir.
Diferansiyel esitlikleri yazabilmek iin hat zerinde sonsuz kk bir eleman dsnelim ve bu elemanün baslangü ve son noktalaründa aküm ve gerilimdeki değismeleri hesaplayalüm. Setiğimiz sonsuz kk eleman hat sonundan x mesafede olsun. Sonsuz kk elemanün uzunluğu da dx olarak kabul edelim.
Buradan,
zdx : Hattün elemanter uzunluğunun seri empedansü
ydx : Hattün elemanter uzunluğunun snt admitansü
olur.
Elemanün yke doğru olan ucunda gerilim Vdir ve kompleks gsterilmistir. V nin değeri hat boyunca değisir. Elemanün genaratre doğru olan ucunda gerilim V+dvdir. Hat zerindeki elemanter uzunlukta artan gerilim xin artüs ynnde dvdir. Dolayüsüyla elemanün genaratre doğru olana ucunda gerilim , yk ucundaki gerilim artü dv olacaktür. xin artüs ynnde artan gerilim aynü zamanda xin artüs ynne ters ynde akan aküm retecek ve bu aküm elemanün empedansü zerinde Izdx gerilim artüsünü meydana getirecektir. Diğer taraftan bu gerilim artüsünün değeri dv olduğundan
dv=Izdx veya 
(1)
yazülabilir.
Benzer sekilde elemandan yke doğru akan aküm Idür. Snt admitans hat boyunca niform dağülmüs olduğundan hat boyunca akümün fazü ve değeri de değisir. Elemanün genaratre yakün küsmünda aküm I+dI olur. Genaratrden sonsuz kk elemana giren aküm elemandan ayrülan akümdan yk ynnde dI kadar byktr. Aralaründaki bu fark elemanün snt admitansündan geen aküm yani Vydx tir. Bylece,
dI=Vydx veya 
(2)
yazabiliriz.
1 ve 2 nolu esitliklerin xe gre diferansiyelini alürsak
elde edilir. 1 ve 2 nolu esitliklerdeki dI/dx ve dV/dx ifadelerini
sürasüyla 3 ve 4 nolu esitliklerde yerine koyarsak, 
(5)
(6) denklemleri bulunur.
Elde edilen 5 ve 6 nolu esitlikler ikinci dereceden lineer diferansiyel denklemler olduğu iin bu denklemlerde gerilim ve akümün zm stel formda olduğu dsnlebilir. Gerilim iin:
V=Aekx zmn ele
alalüm. Ve bu fonksiyonu 5 nolu denklemde yerine koymak iin 
tretilir.
idi. Bu ifadenin ikinci kez diferansiyelini
alürsak;
bulunur. Bu elde edilen
sonularü 5 nolu denklemde yerine koyalüm.
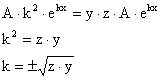
Buradaki kya propagasyon (yayülma) sabiti adü verilir. Kompleks bir byklk olan propagasyon sabiti
seklinde
yazülür.
Propagasyon sabitinin reel küsmü olan azalma sabiti olarak adlandürülür ve birim uzunlukta NEPER olarak llr. Propagasyon sabitinin imajiner küsmü olan ise faz sabiti olarak adlandürülür ve birim uzunlukta radyan olarak llr.
Yukarüdaki denklemlerden retilen genel zm ;
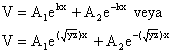(7)
yazülabilir. 7 nolu esitlik ile
verilen V değeri 1 nolu esitlikte yerine konulursa, 
=Karakteristik empedans
A1 ve A2 yi hat sonundaki sartlarü kullanarak belirleyebiliriz.
x = 0 iin (hat sonu kosullarü) V = V2 ve I=I2 olacaktür. Bu değerleri 7 ve 8 nolu denklemlerde yerine koyarsak
9 ve 10 ifadelerini taraf tarafa
toplarsak 
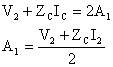
ve taraf tarafa ükarürsak
seklinde yazabiliriz.
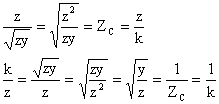
Hat basü değerlerini bulmak iin x = ℓ diyelim ve bulmus olduğumuz A1 ve A2 değerlerini 7 ve 8 nolu denklemlerde yerlerine koyarsak;
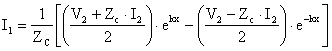bulullnlur.
Bu iki esitlikte gerekli dzenlemeleri yapalüm.
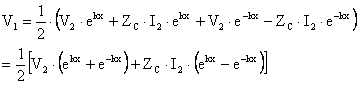
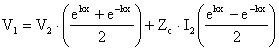
sinhkx coshkx
D
ve 
C
B A
seklinde hat sabitlerini yazmüs oluruz. Buradaki hiperbolik fonksiyonlarün genel aülümlarü;
Uygulamada bir ve ikinci ifadeler düsünda kalanlar ok kk sayülar olduklaründan ihmal edileceklerdir. Bu durumda
rnek 5.
400 km uzunluğundaki bir iletim hattünün empedansü z = 0,1+j0,5 /km , y=j3,2.10-6 S/km olarak veriliyor. Hat sonunda U2 = 215 kV altünda g katsayüsü 1 olan 150 MVA lik bir g ekilmektedir. Hat basüna iliskin aküm ve gerilim değerlerini ABCD katsayülarü ve hiperbolik fonksiyonlar yardümüyla bulunuz.
zm:
a) ABCD katsayülarü ile hat basü parametrelerinin hesaplanmasü:
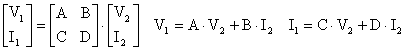
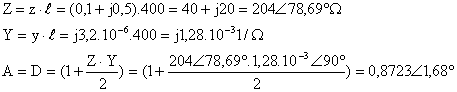
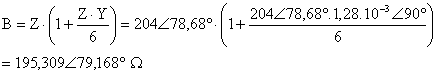
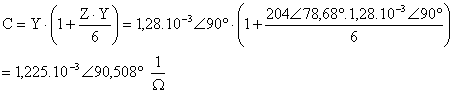
ABCD
katsayülarü bulduktan sonra genel matris formlnden yararlanarak
giris parametrelerini bulunur.Burada bilmediğimiz değer I2
değeridir. I2yi bulmak iin 
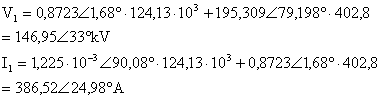
b) Hiperbolik fonksiyonlarla zm:
Bu yoldan gitmek iin Zc ve k değerlerine ihtiyacümüz vardür. Bunlar asağüdaki sekilde hesaplanür.
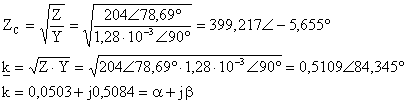
bulunur.
|
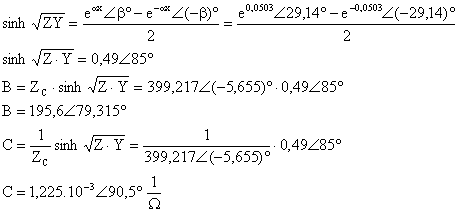
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 2035
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
