SISTEME DE COORDONATE UTILIZATE IN TEHNOLOGIAGPS

SISTEME DE COORDONATE UTILIZATE IN TEHNOLOGIAGPS

Tehnolgia GPS este de obicei asociata cu sistemul de coordonate WGS 84. Acest sistem este un sistem tridimensional elipsoidal si are ca baza elipsoidul WGS 84.

Receptoarele GPS colecteaza informatii de la satelit. In urma prelucrarii semnalului primit de la sateliti (Capitolul 6) coordonatele rezulta pe elipsoidul WGS 84. In tara noastra, dupa cum este bine cunoscut, se utilizeaza sistemul de coordonate Stereografic 1970. Acest sistem are ca elipsoid de baza, elipsodul Krasovski. In acest capitol sunt trecute in revista doar sistemele de coordonate, transformarile de coordonate fiind de fapt un alt capitol. Primul pas spre ajungerea la sistemul de coorodonate Stereografic 1970 consta in trecerea coordonatelor de pe elipsoidul WGS 84 pe elipsoidul Krasovski. Sigur ca dupa ce sunt aduse pe elipsoidul Krasovski, acestea pot fi proiectate si pe alte plane, cunoscute si la noi cum ar fi Gauss fus de 6¿ sau Gauss fus de 3¿, UTM, etc. In cazul sistemelor locale, trecerea se face de obicei prin sistemul Stereografic 1970 sau Gauss pe baza unor puncte comune.

In cazul acestui curs vom prezenta sistemele de coordonate tridimensionale natural si elipsoidal, sistemele plane Stereografic 1970, Gauss Kruger si UTM.

1 Sisteme de coorodonate naturale

Termenul natural defineste suprafata de referinta a sistemului de coorodonate, in cazul nostru Geoidul. De asemenea, marimile care definesc sistemul sau coordonatele sunt referite tot in functie de elemente naturale (latitudine si longitudine astronomica). Acest sistem de coordonate nu este folosit in calculele geodezice deoarece suprafata de referinta, geoidul, este greu calculabila (Volumul I, Capitolul 2.2). Din acest motiv, in mod frecvent se utilizeaza ca suprafata de referinta elipsoidul de rotatie sau sfera de raza medie Gauss.

1.1. Sistemul de coordonate cartezian geocentric

Sistemul de coordonate cartezian geocentric (Figura 1) are ca suprafata de referinta geoidul. Este sistemul de coorodonate fundamental al geodeziei. Este un sistem de coordonate tridimensional rectangular cu centrul in centrul de masa al Pamantului. Pozitia unui punct oarecare P de pe suprafata Pamantului este definita atat in sistem tridimensional cat si in coordonate astronomice. Cele trei axe rectangulare sunt:

Axa Z este axa polilor;

Axa X este in planul ecuatorului si intersecteaza meridianul 0¿;

Axa Y este perpendiculara pe celelalte doua, situata in planul ecuatorului, cu sensul pozitiv spre est.

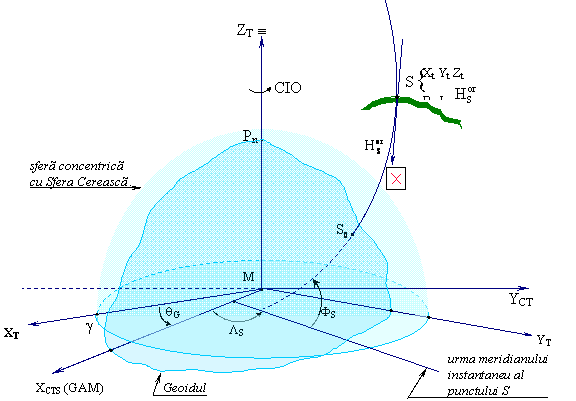
Figura 1. Principalele sisteme de coordonate naturale. Sistemul de coordonate natural

Coordonatele astronomice sunt:

latitudinea astronomica, notata F;

longitudinea astronomica, notata L.

Pentru a defini pozitia punctului nu pe geoid ci pe suprafata terenului, acestor doua coorodonate li se adauga altitudinea ortometrica, notata H^OR.

Latitudinea astronomica, F, a punctului S este unghiul format de verticala punctului S cu planul ecuatorial al geoidului. Longitudinea astronomica, L, este unghiul diedru format de meridianul astronomic al punctului Greenwich cu meridianul punctului S. Altitudinea ortometrica, H^OR, este diferenta pe verticala, masurata pe verticala locului, dintre punctul S de pe suprafata terenului si punctul in care verticala punctului S inteapa geoidul. Fizic, verticala unui punct oarecare S este data de firul cu plumb. Toate observatiile geodezice sunt referite la verticala locului, care trebuie sa coincida cu axa verticala a oricarui aparat geodezic (statie totala, receptor GPS, nivela) amplasat in punctul respectiv.

1.2. Sistemul astronomic local.

Sistemul de coordonate prezentat mai sus este un sistem tridimensional si nu poate fi utilizat in lucrarile topografice curente. Pe intinderi mici este nevoie ca suprafetele de teren sa fie prezentate pe planuri. Orice suprafata de teren este de la sine inteles ca este o calota sferica. In momentul proiectarii pe un plan se produc anumite rupturi, apar anumite erori pe distante, pe unghiuri, in calculul suprafetelor. Daca planul pe care se proiecteaza suprafata de interes este tangent la suprafata respectiva (o suprafata mica), atunci deformatiile datorate proiectiei sunt minime. Planul nou creat trebuie sa aiba un sistem de coordonate local plan bine definit. De asemenea, trebuie definit datumul de referinta (Capitolul 6 din Cursul de topografie geodezie, Volumul II). Ca punct fundamental sau de origine al sistemului de coordonate (topocentru) poate fi ales punctul P de pe suprafata pamantului. Oricare punct de pe suprafata fizica a Pamantului poate deveni origine a unui sistem de coordonate (topocentru). Acest nou sistem de coordonate (Figura 1), astronomic local, are axele definite astfel:

planul orizontal x_ay_a este perpendicular pe directia gravitatii;

axa x_a este situata in meridianul local al punctului P (originea sistemului), deci cu sensul pozitiv spre nordul geografic;

axa y_a are sensul pozitiv spre estul astronomic si este perpendiculara atat pe axa x_a cat si pe directia gravitatii;

altitudinea, H^OR, definita si mai sus, este indreptata dupa tangenta la directia gravitatii, cu sensul pozitiv catre zenitul astronomic.

Orice alt punct din vecinatatea punctului P si vizibil din acest punct, poate fi determinat in acest sistem de coordonate prin masuratori clasice (directii, distante, unghiuri zenitale) sau GPS. Masuratorile clasice sunt denumite si coordonate astronomice polare locale:

D - distanta inclinata dintre cele doua puncte;

a- azimutul astronomic al punctului de statie in raport de punctul nou, R;

z - unghiul zenital, format intre verticala locului punctului P si directia PR;

Coordonatele astronomice polare locale care definesc pozitia punctului nou R in sistemul astronomic local pot fi transformate in coordonate naturale locale, respectiv x_ay_a H^OR, pentru punctul R.

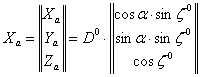(1)

2 Sisteme de coordonate conventionale

Dupa cum am precizat anterior, in practica geodezica, geoidul este inlocuit cu un elipsoid de rotatie. Alegerea unui elipsoid de rotatie nu se face intamplator. Este necesar ca elipsoidul ales sa fie foarte apropiat de geoid in zona de interes. In prezent se utilizeaza elipsoidul WGS84 care aproximeaza cel mai bine geoidul si este utilizat de toate tarile care efectueaza determinari GPS.

2.1 Ecuatiile parametrice ale elipsoidului de rotatie.

Elipsoidul de referinta, adica elipsoidul folosit la un moment dat, intr-o tara sau mai multe tari, pentru rezvolvarea problemelor geodezice, este un elipsoid de rotatie cu turtire mica la poli.

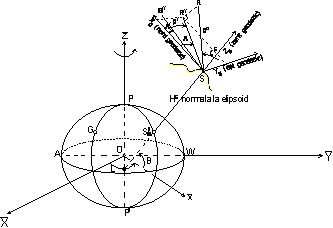
Fig. 2 Principalele sisteme de coordonate naturale. Sistemul de coordonate elipsoidal

Ecuatia generala a unui elipsoid de rotatie, exprimata sub forma impicita:

(2)

este putin folosita in geodezia elipsoidala.

Parametrii geometrici prin care se poate defini, geometric, un elipsoid de rotatie sunt:

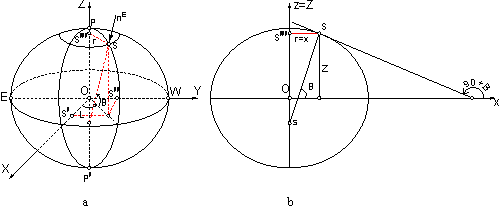
Fig. 3 Semiaxa mare (raza ecuatoriala)

- semiaxa mica; (4)

- turtirea (geometrica); (5)

- excentricitatea liniara; (6)

- prima excentricitate (numerica); (7)

- a doua excentricitate (numerica); (8)

- raza de curbura polara. (9)

Primii trei parametri se mai numesc si parametri geometrici principali.

Definirea elipsoidului de rotatie se face prin doi parametri geometrici (din cei mentionati), dintre care unul trebuie sa fie liniar.

In tabelul 1 se prezinta valorile numerice ale parametrilor a si f pentru elipsoizii de referinta care au fost utilizati in decursul anilor in tara noastra, precum si pentru elipsoidul recomandat de AIG in anul 1980.

Tabelul 1 Elipsoizi de referinta folositi in Romania

Relatiile principale de legatura dintre parametrii geometrici ai elipsoidului de rotatie sunt:

(10)

(11)

(13)

(14)

(15)

(16)

Prin dezvoltari in serie se obtine de asemenea:

(17)

In geodezia elipsoidala se opereaza frecvent cu ecuatiile parametrice, in functie de coordonatele B si L, adica:

X = X (B, L);

Y = Y (B, L);

Z = Z (B, L).

Pentru deducerea acestora este util sa se determine, in prealabil, ecuatiile parametrice ale elipsei meridiane:

x = x (B); z = z (B),

deoarece legatura dintre coordonatele X, Y, Z si respectiv x, z (fig. 2) este imediata:

X = x cos L; Y = x sin L; Z = z. (18)

Ecuatia elipsei meridiane sub forma implicita este:

(19)

sau, in functie de (11):

(20)

Coeficientul unghiular al tangentei la elipsa in punctul S (fig. 2, b) poate fi exprimat sub forma:

(21)

sau sub forma:

(22)

Din egalarea ultimelor doua relatii rezulta:

(23)

Introducand expresia (23) in (20) se obtine:

(24)

iar, in continuare, din relatia (23):

(25)

Ultimele doua relatii reprezinta ecuatiile parametrice ale elipsei meridiane in functie de latitudinea geodezica B. Pentru scrierea mai concentrata a acestor ecuatii, precum si pentru usurarea calculelor practice, se folosesc frecvent urmatoarele functii auxiliare:

(26)

(27)

unde:

(28)

Folosind relatiile de legatura dintre parametrii elipsoidului de referinta (10) - (17), rezulta:

(29)

In acest mod, ecuatiile parametrice ale elipsei meridiane (24) si (25) se pot exprima si sub forma:

Utilizand aceste ecuatii, precum si relatiile (18) rezulta ecuatiile parametrice ale elipsoidului de rotatie:

(31)

2.2. Sistemul global elipsoidal.

Sistemul global elipsoidal este similar cu sistemul cartezian global geocentric. Originea sistemului este in imediata apropiere a centrului sistemului cartezian global geocentric, respectiv cat mai aproape de centrul de masa al Pamantului. De asemenea, cele trei axe de coordonate sunt apropiate pana la coincidenta cu axele de coordonate ale sistemului cartezian global geocentric. Este de asemenea un sistem de coordonate tridimensional rectangular. Pozitia unui punct oarecare P de pe suprafata Pamantului este definita atat in sistem tridimensional elipsoidal cat si in coordonate elipsoidale (latitudinea si longitudinea elipsoidala) (figura 2). Cele trei axe rectangulare sunt:

Axa Z' este cat mai aproape de axa polilor geografici;

Axa X' este in planul ecuatorului elipsoidal si intersecteaza meridianul 0¿ al elipsoidului respectiv;

Axa Y' este perpendiculara pe celelalte doua, situata in planul ecuatorului elipsoidului, cu sensul pozitiv spre est.

Coordonatele elipsoidale, analog coordonatelor astronomice sunt:

latitudinea geodezica, notata B;

longitudinea geodezica, notata L.

Pentru a defini pozitia punctului nu pe elipsoid ci pe suprafata terenului, acestor doua coorodonate li se adauga altitudinea elipsoidala, notata H^E.

Latitudinea geodezica, B, a punctului P este unghiul format de normala la elipsoid in punctul P cu planul ecuatorului elipsoidului de referinta. Longitudinea geodezica, L, este unghiul diedru format de meridianul geodezic al punctului P cu meridianul geodezic al punctului Greenwich. Altitudinea elipsoidala, H^E, este diferenta pe verticala, masurata pe normala la elipsoid a punctului P, dintre punctul P de pe suprafata terenului si punctul in care normala le elipsoid a punctului P inteapa elipsoidul.

De remarcat ca meridianul 0⁰ al elipsoidului nu corespunde cu meridianul 0⁰ al geoidului. De asemenea, in mod normal, fiecare elipsoid are alta origine pentru meridianul 0⁰ si alta pozitie a ecuatorului. De exemplu, intre elipsoidul Krasovski si elipsoidul WGS84 este o diferenta de circa 1" pe longitudine si circa 6" pe latitudine la nivelul tarii noastre.

2. Sistemul elipsoidal local.

Asa cum am definit sistemul astronomic local, tot astfel este definit si sistemul elipsoidal local (Figura 2).

Sistemul de coordonate, elipsoidal local, are axele definite astfel:

planul orizontal x_ey_ae este perpendicular pe normala la elipsoid;

axa x_e este situata in meridianul geodezic al punctului P (originea sistemului), deci cu sensul pozitiv spre nordul geodezic;

axa y_e are sensul pozitiv spre estul geodezic si este perpendiculara atat pe axa x_e cat si pe normala la elipsoid;

altitudinea, H^E, definita si mai sus, este indreptata dupa normala la elipsoid, cu sensul pozitiv catre zenitul geodezic.

Coordonatelor astronomice polare le corespund coordonatele elipsoidale polare locale:

D - distanta inclinata dintre cele doua puncte;

A - azimutul astronomic al punctului de statie in raport de punctul nou, R;

x^E - unghiul zenital, format intre normala la elipsoid a punctului P si directia PR;

Coordonatele elipsoidale polare locale care definesc pozitia punctului nou R in sistemul elipsoidal local pot fi transformate in coordonate elipsoidale locale, respectiv x_ey_e H^E, pentru punctul R.

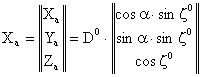
3 Sisteme de coorodonate plane

1 Sistemul de coordonate Stereografic 1970

Proiectia stereografica 1970 este proiectia oficiala folosita in prezent in Romania.

1.1. Definitie si caracteristici principale. Proiectia azimutala perspectiva plan secant are polul proiectiei in punctul Q_o de coordonate B_o = 46 si L_o = 25 est Greenwich. Proiectia a fost adoptata incepand cu luna septembrie 1971 cand a fost emis decretul nr. 305 "cu privire la activitatea geodezica, topo-fotogrammetrica si cartografica". A fost preluat, ca suprafata de referinta, elipsoidul Krasovski. Avantajul aceste proiectii este reprezentarea intregii tari pe un singur plan. Cercul de deformatie nula are raza de 201.718 m si reprezinta intersectia planului secant cu elipsoidul de rolatie. Originea sistemului de axe de coordonate rectangulare este in punctul Q_o, axa x fiind indreptata catre nord, iar axa y catre est.

1.2. Formulele de transformare a coordonatelor B, L in x, y si respectiv x, y in B, L se bazeaza pe formule cu coeficienti constanti (Falie & Strutu, 1957, Calistru & Munteanu, 1975 s. a.).

Formulele cu coeficienti constanti sunt exprimate in functie de diferenta de latitudine DB si de diferenta longitudine DL dintre punctul care se transcalculeaza (de coordonate B, L) si polul proiectiei Q_o. S-au folosit metodele propuse de Vladimir Hristov in anul 1937 care constau in dezvoltarea in serie Taylor, in jurul punctului central Q_o, a tuturor elementelor care depind de latitudine (latitudinea izometrica q, raza paralelului r, etc.). Coeficientii constanti sunt derivatele calculate in punctul central. Operatiunile de transcalcul incep prin calcule pregatitoare:

a. Transformarea coordonatelor geodezice B, L in coordonate rectangulare x, y.

(33)

(34)

Intr-o prima etapa se calculeaza coordonatele x^/ si y^/ in plan tangent la elipsoid:

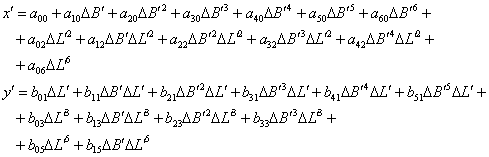(35)

Valorile coeficientilor constanti sunt:

In urmatoarea etapa se determina coordonatele in planul secant:

(36)

in care: c = 0,999750000.

Pentru determinarea coordonatelor finale fata de originea Q₀, se adauga valorile 500.000 pe x si pe y.

b. Transformarea coordonatelor rectangulare x, y in coordonate geodezice B, L.

Si pentru aceasta transformare sunt necesare urmatoarele calcule pregatitoare:

Trecerea coordonatelor plane rectangulare x, y din planul secant in planul tangent;

(37)

in care: c^/ = 1,00025006

Pentru omogenizarea ecuatiilor coordonatele rectangulare x^/ si y^/ se multiplica in prealabil cu factorul 10^-5.

Transformarea coordonatelor rectangulare x, y din plan tangent in coordonate geodezice B, L se realizeaza cu relatiile:

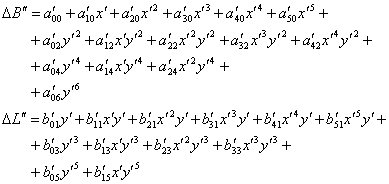(38)

1. Deformatiile in proiectia stereografica 1970. Deformatia liniara, descrisa in (cap. 5, vol 1) are aceeasi valoare pe vertical si almucantarat:

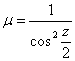(39)

In proiectia stereografica 1970 deformatiile liniare in interiorul cercului de secanta sunt negative, ajungand pana la -25 cm in polul Q_o al proiectiei. Pe linia cercului de secanta deformatiile liniare sunt nule, iar in afara cercului de secanta deformatiile liniare sunt pozitive.

Rezulta pentru deformatia unghiulara (vol 1, cap. 5, 5.3):

(40)

adica proiectia stereografica 1970 este conforma. Modulul de deformatie a suprafetelor (vol 1, cap. 5, 5.2), este:

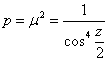(41)

2 Sistemul de coordonate Gauss Kruger

Proiectia Gauss-Krger. Aceasta proiectie a fost introdusa in tara noastra in anul 1951. Din anul 1971, in lucrarile civile, proiectia Gauss-Krger a fost inlocuita cu proiectia stereografica 1970. Specialistii militari folosesc in continuare proiectia Gauss-Krger.

2.1. Definitie si caracteristici principale. Proiectia Gauss-Krger este o proiectie cilindrica transversala, conforma si are ca suprafata de referinta elipsoidul Krasovski. Specific proiectiei este reprezentarea elipsoidului pe fuse, adica pe portiuni delimitate de meridiane situate la latitudini diferite, in functie de scopul urmarit. Astfel, fusele pot fi de 6 sau de 3 sau mai mici (pentru reprezentari la scari mari). Orice fus, indiferent de marime, are un meridian axial, a carui longitudine B_o este precizata in raport de meridianul origine. Conform unei intelegeri internationale, aceeptata si de tara noastra, numerotarea fuselor de 6 se face cu cifre arabe, de la 1 la 60, spre est, de la meridianul de 180, care separa fusele numarul 1 (cuprins intre 174 si 180 longitudine vestica) si numarul 60 (cuprins intre 174 si 180 longitudine estica). Tara noastra se reprezinta in fusele de 6 cu numarul 34 (B_o = 21 est Greenwich) si numarul 35 (B_o = 27 est Greenwich).

Meridianul axial al fusului se reprezinta in plan printr-o linie dreapta, care se ia ca axa O|0 (sensul pozitiv spre nord) a sistemului de coordonate plane pentru fusul respectiv. Axa Oy este perpendiculara pe axa Ox si cu sensul pozitiv spre est.

2.2. Formulele de transformare a coordonatelor B, L in x, y si respectiv x, y in B, L se bazeaza pe formule cu coeficienti constanti (Falie & Strutu, 1957, Calistru & Munteanu, 1975 s. a.), principiile de deducere a acestora fiind similare cu cele descrise in (vol 1, cap. 5, 5.5.1.5.).

a. Transformarea coordonatelor geodezice B, L in coordonate rectangulare x, y.

Si in aceasta transformare sunt necesare unele calcule pregatitoare:

(42)

in care B_o = 46, iar L_o = longitudinea meridianului axial al fusului respectiv.

(43)

Intr-o prima etapa se calculeaza coordonata Dx si coordonata y raportate la fusul respectiv:

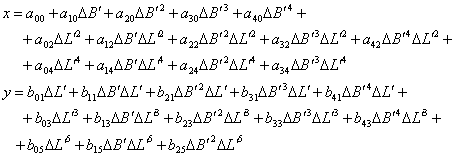(44)

Valorile coeficientilor constanti sunt urmatoarele:

Coordonata finala x rezulta din: x = Dx + x_o, in care x_o = 5096175,747 m.

b. Transformarea coordonatelor rectangulare x, y in coordonate geodezice B, L.

Initial se calculeaza diferenta Dx = x - x_o in care x_o a fost definit anterior.

Pentru omogenizarea calculelor de transformare, coordonatele rectangulare Dx si y se multiplica cu factorul 10^-5.

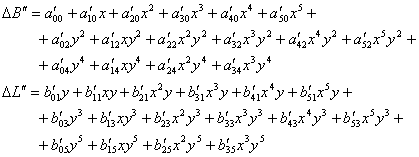(45)

Coeficientii constanti de mai sus au valorile:

Pentru calculul coordonatelor B si L se folosesc formulele (42).

2. Deformatiile in proiectia Gauss-Krger.

Modulul de deformatie liniara (vol 1, cap. 5, 5.1) are forma:

(46)

in care y^/ este departarea punctului considerat fata de meridianul axial.

Se observa ca deformatia liniara creste cu patratul departarii fata de meridianul axial si este nula pe acesta.

Deformatia unghiulara (vol 1, cap. 5, 5.3) este nula deoarece semiaxele elipsei deformatiilor sunt egale.

Modulul de deformatie a suprafetelor (vol 1, cap. 5, 5.2):

p = m

3 Sistemul de coordonate UTM

Proiectia UNIVERSAL TRANSVERSAL MERCATOR (UTM)

Proiectia MERCATOR este o proiectie cilindrica si are mai multe variante, in functie de pozitia cilindrului. Cand cilindrul este tangent la ecuatorul elipsoidului, proiectia este normala sau directa. Cand cilindrul este tangent la un meridian dat, proiectia este transversala. Proiectia MERCATOR a fost definita in anul 1569 de catre matematicianul olandez GERHARD KREMER cunoscut si sub pseudonimul MERCATOR (1512-1594). Varianta normala a fost folosita initial de MERCATOR si descrisa apoi de WRIGHT (1599). Varianta transversala a fost descrisa de LAMBERT in anul 1772, dezvoltata de GAUSS intre anii 1825-1830 si adaptata pentru cartografie de KRUGER in anul 1912. Datorita acestui fapt, varianta transversala poarta si numele de proiectie conforma GAUSS-KRUGER. In anul 1950 s-a inceput elaborarea unui sistem de referinta universal, pentru intreaga suprafata terestra, introdus pentru hartile topografice utilizate de tarile membre NATO denumit UTM (Universal Transversal Mercator). Prin sistemul de proiectie UTM se poate reprezenta aproape intreaga suprafata a globului terestru cu exceptia zonelor polare.

Sistemul UTM acopera suprafata cuprinsa intre paralela de 80^o latitudine sudica si paralela de 84^o latitudine nordica. Datorita acestui fapt fusele terestre cu latime de 6^o in longitudine (definite la fel ca si in proiectia GAUSS-KRUGER) cuprinse intre aceste paralele poarta denumirea de zone. Peste limita de 84^o latitudine nordica pana la pol, respectiv peste limita de 80^o latitudine sudica pana la pol se aplica un alt sistem de proiectie denumit UPS (Universal Polar Stereografic).

Sistemul UTM este deosebit de alte proiectii cilindrice prin faptul ca parametrii proiectiei UTM au fost calculati pentru mai multi elipsoizi de referinta diferiti, in scopul de a ajunge la o unificare mondiala, astfel: CLARKE 1886 (America de Nord), CLARKE 1880 (Africa), BESSEL 1841 (fostele tari sovietice, Japonia si partea de sud-est a Asiei), EVEREST 1830 (India si partile alaturate ale sud-estului Asiei) si HAYFORD 1909 (celelalte parti ale lumii). In urma progreselor facute in geodezia spatiala, in anul 1984 s-a introdus proiectia UTM pe elipsoidul asociat sistemului WORLD GEODETIC SYSTEM 1984, determinat cu ajutorul satelitilor artificiali ai Pamantului. Elipsoidul de rotatie ales astfel este WGS84, folosit pentru utilizarea in scopuri militare si civile a sistemului de pozitionare cu sateliti GPS (GLOBAL POSITIONING SYSTEM).

Parametrii care definesc un elipsoid (pentru urmatoarele definitii se vor considera toate lungimile exprimate in metri si toate coordonatele geografice in radiani, daca nu este specificat altceva) sunt stabiliti dupa cum urmeaza:

(pentru emisfera Sudica si Vestica se foloseste notatia negativa)

a = semiaxa mare a elipsoidului

b = semiaxa mica a elipsoidului

f = turtirea =

e² = (prima excentricitate)² = = f (2-f)

e'² = (a doua excentricitate)² = = =

n = =

= raza de curbura a meridianului =

= raza de curbura in primul vertical = = (1+e'²cos²)

S = arcul de meridian = A'- B'sin2+C'sin4-D'sin6+E'sin8

unde:

(E' 0.03mm)

Parametrii proiectiei UTM sunt definiti dupa cum urmeaza:

= latitudinea

= longitudinea

' = latitudinea piciorului perpendicularei duse din punct pe meridianul central

_o = longitudinea originii proiectiei (meridianul central)

_o = diferenta longitudinii fata de meridianul central

k_o = factorul de scara central care reprezinta o reducere arbitrara aplicata tuturor lungimilor geodezice pentru a reduce deformarea maxima de scara a proiectiei = 0.9996

k = factorul de scara in punctul de lucru pe proiectie

FN = Fals Nord (0m pentru emisfera Nordica si 10000000m pentru emisfera Sudica)

FE = Fals Est (500000m)

E = E - FE

E = valoarea coordonatei rectangulare Est

N = valoarea coordonatei rectangulare Nord

C = convergenta meridianelor

Termenii utilizati in calculul ecuatiilor generale ale proiectiei UTM sunt:

T₁ = Sk_o

T₂ =

T₃ =

T₄ =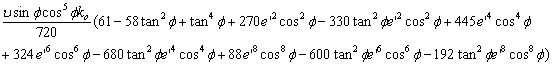

T₅ =

T₆ =

T₇ =

T₈ =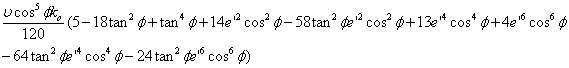

T₉ =

T₁₀ =

T₁₁ =

T₁₂ =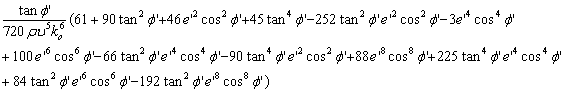

T₁₃ =

T₁₄ =

T₁₅ =

T₁₆ =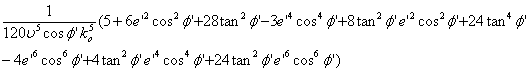

T₁₇ =

T₁₈ = sin

T₁₉ =

T₂₀ =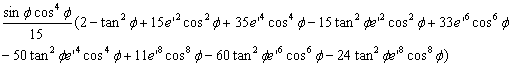

T₂₁ =

T₂₂ =

T₂₃ = `

T₂₄ =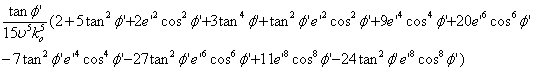

T₂₅ =

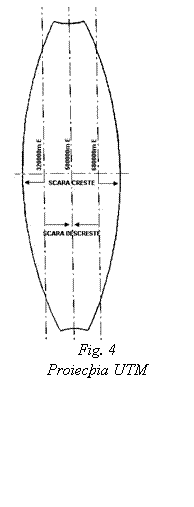T₂₆ =

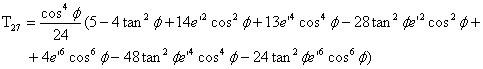
T₂₈ =

T₂₉ =

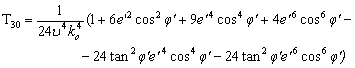
T₃₁ =

Calculele, utilizand termenii de mai sus, asigura o precizie de aproximativ 0.001 secunde de arc pentru coordonatele geografice si de 0.01m pentru coordonatele rectangulare.

Transformarea coordonatelor geografice in coordonate rectangulare:

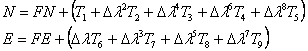
Transformarea coordonatelor rectangulare in coordonate geografice:

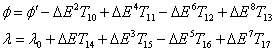
Latitudinea se obtine prin iteratii succesive bazate pe termenul T1.

Convergenta meridianelor (din coordonate geografice):

Convergenta meridianelor (din coordonate rectangulare):

Factorul de scara (din coordonate geografice):

Factorul de scara (din coordonate rectangulare):

Proiectia UTM prezinta avantajul reducerii deformatiilor liniare prin introducerea unui factor de scara subunitar de-a lungul meridianului axial (central) al fusului (zonei). In proiectia GAUSS-KRUGER deformatiile liniare de-a lungul meridianului axial (central) al fusului sunt nule (modulul de deformatie liniar este egal cu 1), acestea crescand pe masura ce ne indepartam de meridianul axial, ajungand la o valoare maxima in apropierea meridianelor din marginile fusului (la latitudinea medie a Romaniei deformatiile ajung la aproximativ 75-77 cm/km). In proiectia UTM aceste deformatii maxime, in vecinatatea meridianelor din marginile fusului, se injumatatesc prin introducerea factorului de scara subunitar de-a lungul meridianului axial al fusului (zonei). Factorul de scara subunitar care apare de-a lungul meridianelor axiale ale zonelor se datoreaza faptului ca, in acest caz, cilindrul nu mai este tangent la meridianul axial (central) al zonei ca la proiectia GAUSS-KRUGER, ci secant. Intersectia dintre suprafata terestra si suprafata cilindrului se face dupa doua meridiane numite meridiane de secanta. Proiectia UTM face parte din grupa proiectiilor cilindrice transversale conforme, care dau o reprezentare a elipsoidului de referinta direct pe planul cilindrului. Reprezentarea suprafetei terestre se face pe zone de 6^o diferenta de longitudine, proiectia UTM fiind o proiectie conforma, deci unghiurile nu sunt deformate (modulul de deformatie unghiular este egal cu 1). Datorita faptului ca deformatiile liniare sunt mici, iar deformarile unghiulare sunt nule, creste precizia reprezentarii terenului pe o harta topografica executata in proiectia UTM. Zonele in proiectia UTM se numeroteaza incepand de la meridianul de longitudine 180^o (meridianul opus meridianului care trece prin punctul Greenwich), cu cifre arabe de la 1 la 60, in sens antiorar.

Suprafata elipsoidului pe plan se proiecteaza astfel:

reprezentarea este conforma (modulul de deformatie unghiulara este nul);

reprezentarea meridianului axial (central) al unei zone este o dreapta fata de care proiectia este simetrica;

factorul de scara pe directia meridianului axial este k_o = 0.9996, deci cilindrul care este circumscris elipsoidului nu mai este tangent la meridianul axial, ca in cazul proiectiei GAUSS-KRUGER, ci secant, dupa doua meridiane simetrice fata de meridianul axial, numite meridiane de secanta;

sistemul de coordonate este propriu fiecarui fus.

Intr-o zona de 6^o exista linii de secanta (cu deformatii liniare nule) situate la aproximativ 180000m E si V fata de meridianul axial (central) al zonei respective.

Pentru evitarea coordonatelor negative, meridianului axial (central) i se atribuie o valoare falsa a estului de 500000m, practic, meridianul axial al zonei de 6^o este translatat spre stanga cu 500000m.

Astfel meridianele de secanta se afla la coordonata 320000m E si respectiv 680000m E.

Axele sistemului rectangular al unei zone de 6^o in proiectia UTM sunt inversate fata de proiectia GAUSS- KRUGER:

axa Ox (abscisa) este pe orizontala si este data de proiectia ecuatorului in planul hartii topografice.

axa Oy (ordonata) este pe verticala si este data de proiectia meridianului central (axial) al zonei respective.

In proiectia U.T.M. factorul de scara este 1.000 de-a lungul liniilor (meridianelor) de secanta, descreste pana la 0.9996 de-a lungul meridianului axial si creste pana la 1.0010 in zonele meridianelor de la marginile zonei.

Meridianele si paralele se reprezinta in proiectia UTM prin curbe oarecare, meridianele fiind simetrice fata de meridianul axial al zonei care conform conditiei puse se reprezinta printr-o linie dreapta.

Paralelele sunt simetrice fata de Ecuator, care se reprezinta printr-o linie dreapta.

Pozitia unui punct oarecare in planul proiectiei (in planul hartii) se determina intr-o retea de coordonate rectangulare X, Y. Grila rectangulara se realizeaza ducand linii paralele la axele de coordonate ale fiecarei zone.

Toate coordonatele X in proiectia UTM contin translatia de 500000m. Pentru a afla pozitia exacta a unui punct oarecare fata de meridianul central al zonei respective, se va scadea 500000m din valoarea coordonatei X.

In emisfera sudica apare particularitatea referitoare la coordonatele Y (ordonate) negative. Pentru a evita coordonate negative in emisfera sudica se adopta ca Ecuatorul sa aiba ordonata de 10000000m (valabil numai pentru coordonatele din emisfera sudica). Aceasta valoare se justifica astfel: de la Ecuator la Polul Sud sunt 90^o latitudine, distanta de teren acoperita de 1^o de latitudine este de cca. 111 km, deci: 90^o x 111km 9900000m 10000000m

Coordonatele geografice sunt exprimate in masuri unghiulare, mai precis in grade sexazecimale incepand cu valoarea de 0^o la Ecuator, paralelele fiind numerotate pana la valoarea de 84^o N si 80^o S. Deoarece latitudinea poate avea aceeasi valoare numerica la N sau la S de Ecuator, se va indica intotdeauna directia N sau S.

Longitudinea se masoara atat spre Est cat si spre Vest incepand de la meridianul de origine (meridianul ce trece prin punctul Greenwich). Meridianele la Est de meridianul origine merg pana la valoarea de 180^o si sunt dentificate ca longitudine estica. Similar se procedeaza si cu longitudinile vestice.

Romania se afla pe fusele 34 si 35, marginea de jonctiune dintre cele doua zone este meridianul de longitudine de 24^o, situat aproximativ la jumatatea Romaniei.

Existenta mai multor zone in proiectia UTM (ca si in cazul proiectiei GAUSS-KRUGER) impune posibilitatea transformarii coordonatelor dintr-un fus in celalalt. Aceasta operatiune este ceruta in cazul unor lucrari care se executa pe suprafete a doua zone invecinate (adiacente).

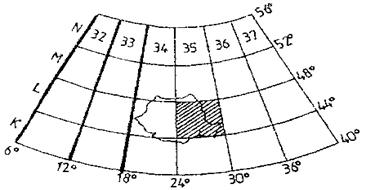
Fig. 5. Nomenclatura foilor de harta in proiectia UTM

Nomenclatura reprezinta un sistem de pozitionare a foilor pe harta pe suprafata globului terestru si totodata o metoda de identificare unica a acestora.

Nomenclatura foilor de harta in proiectia UTM este diferita de aceea pentru foile de harta in proiectia GAUSS-KRUGER.

In proiectia GAUSS-KRUGER, ca scara de baza se utilizeaza 1:25000, iar in proiectia UTM sunt utilizate doua scari de baza si anume: 1:50000 si 1:250000.

Nomenclatura unei foi de harta la scara 1:250000 este formata din doua grupuri de caractere alfanumerice despartite prin linioara astfel:

-primul grup este alcatuit din doua litere si doua cifre cu urmatoarea semnificatie:

prima litera reprezinta emisfera nordica (N) sau emisfera sudica (S);

a doua litera reprezinta intervalul de 4^o pe latitudine in care se afla foaia.

Numerotarea incepe cu litera A de la Ecuator spre N si S. Ordinea literelor este cea din alfabetul latin (de la A la V).

grupul de doua cifre reprezinta numarul zonei (fusului in proiectia GAUSS-KRUGER). Dupa cum stim, Romania se afla pe zonele (fusele) 34 si 35.

al doilea grup de caractere este format dintr-un numar ce reprezinta pozitia foii intr-un cadru de 4^o pe latitudine si 6^o pe longitudine.

Exemplu: NL 34-06 se citeste astfel:

N = emisfera nordica;

L = intervalul cuprins intre paralelele de 44^o si 48^o latitudine;

34 = zona 34 (a patra de la Greenwich spre est) care

este cuprinsa intre meridianele de 18^o si 24^o longitudine;

06 = a sasea foaie de harta din zona de 4^o latitudine si 6^o longitudine;

Ca si in proiectia GAUSS-KRUGER, harta la scara 1:1.000.000 a fost luata ca baza pentru hartile la scara 1:250.000. Deci, pentru obtinerea unei foi de harta la scara 1:250.000 s-a impartit foaia de harta la scara 1:1.000.000 in 16 foi de harta la scara 1:250.000 daca suprafata reprezentata este cuprinsa intre ecuator si paralela de 40^o latitudine nordica respectiv intre ecuator si paralela de 40^o latitudine sudica. Dimensiunea unei astfel de foi de harta la scara 1:250.000 este de 1^o pe latitudine si 1^o30' pe longitudine.

Foaia de harta la scara 1:1.000.000 se imparte in 12 foi de harta la scara 1:250.000 daca suprafata reprezentata este cuprinsa intre paralela de 40^o latitudine nordica si paralela de 84^o latitudine nordica respectiv intre paralela de 40^o latitudine sudica si paralela de 80^o latitudine sudica. Dimensiunea unei astfel de foi de harta la scara de 1:250.000 este de 1^o pe latitudine respectiv de 2^o pe longitudine.

Nomenclatura unei foi de harta la scara 1:250.000 se compune deci din nomenclatura foii de harta la scara 1:1000000 si numarul foii de harta rezultat din impartire.

Nomenclatura foii de harta la scara 1:50.000 are ca baza tot harta la scara 1:1.000.000, dar denumirile pornesc de la zonele si subzonele delimitate de interesul NATO.

Dimensiunea unei foi de harta la scara 1:50.000 in zona Romaniei este de 15' pe latitudine si 18' pe longitudine. (In proiectia GAUSS-KRUGER, foile de harta la scara 1:50.000 au dimensiunile de 10' pe latitudine si 15' pe longitudine).

Suprafata reprezentata la scara 1:50.000 in proiectia UTM este mai mare astfel decat suprafata reprezentata la aceasta scara in proiectia GAUSS-KRUGER.

Foaia de harta la scara de 1:100.000, avand dimensiunile de 30' pe latitudine si 36' pe longitudine, se obtine prin impartirea unei foi de harta la scara 1:1.000.000 in 80 de planse.

Dimensiunile cadrului foii de harta la scara 1:50.000 rezulta din impartirea foii de harta la scara 1:100.000 in patru.

Retelele rectangulare militare constau din linii paralele ce se intersecteaza sub unghiuri drepte si care formeaza o retea rectangulara. Liniile N - S se numesc norduri, iar liniile E - V se numesc esturi.

Intervalul dintre doua linii succesive ale unui astfel de caroiaj rectangular este functie de scara hartii topografice militare respective.

Pentru zonele terestre cuprinse intre latitudinile de 84^o N si 80^o S se utilizeaza reteaua rectangulara UTM, deci si pentru Romania.

Caroiajul rectangular militar de referinta (MGRS) a fost proiectat pentru a fi utilizat impreuna cu caroiajul rectangular UTM.

MGRS reprezinta versiunea alfa numerica a coordonatelor rectangulare numerice UTM.

Globul terestru a fost divizat in 60 de zone (fuse) de 6^o longitudine si fasii latitudinale de 8^o (20 de astfel de fasii latitudinale, incepand de la paralela de 80^o S si pana la paralela de 84^o N).

Fasiile latitudinale se noteaza cu literele alfabetului latin, majuscule incepand cu litera C si terminand cu litera X, exceptand literele I si O (fasia X are 12^o).

Zonele de 6^o se numeroteaza de la 1 la 60 incepand de la antemeridian in sens antiorar.

Deci, o regiune oarecare de pe glob este localizata in sistemul MGRS prin identificarea zonei terestre (zona de 6^o si fasia latitudinala de 8^o).

Aceasta identificare este unica si se numeste "denumirea zonei retelei".

Romania se intinde in zonele UTM 34 si 35 si in banda de latitudine T.

4 Sisteme de coordonate locale

In capitolele 1.2 si 2.3 au fost discutate Sistemul astronomic local si sistemul elipsoidal local. De aici se poate deduce ca orice punct de pe suprafata terestra poate deveni originea unui sistem de coordonate local.

Sistemele de coordonate locale sunt create pentru lucrari de mica anvergura sau pentru lucrari ingineresti. Astfel, se alege un plan de proiectie si un sistem de axe de coordonate care sa satisfaca nevoile locale. In multe cazuri sistemul de coordonate este legat la sistemul Stereografic 1970 printr-un punct origine care are coordonatele in sistem stereografic 1970. Se alege o orientare catre un punct al retelei, iar distanta redusa la planul de proiectie este aceeasi cu distanta redusa la orizont. In acest mod se face o legatura cu proiectia nationala. Este totusi periculoasa aceasta practica, deoarece toate celelalte puncte ale retelei locale (in afara punctului origine care are coorodnate identice in sistem stereografic si local) vor avea coordonate in sistem local, dar foarte apropiate de valorile absolute in sistem Stereografic 1970. In acest mod se pot crea confuzii cand se calculeaza coordonatele punctelor de indesire. Astfel de cazuri concrete sunt la Arad si Craiova. La Arad, datorita deformatiilor foarte mari in sistemul Streografic 1970, reteaua locala a municipiului a fost proiectata pe un plan local. Punctul de plecare al retelei locale are aceleasi coordonate in ambele sisteme. Celelalte puncte ale retelei locale au coordonate in sistem local, dar foarte apropiate de valorile lor in sistemul national. Valorile absolute incep sa difere semnificativ in cele doua sisteme de coordonate spre marginea localitatii (diferente de circa 2 metri pe x si 2 metri pe y). Este foarte periculos, deoarece pentru utilizatorii obisnuiti aceste diferente nu sunt bine intelese si se creaza confuzii.

Exista utilizatori care nu pot face legarea la reteaua nationala si in acest caz, pentru fiecare parcela, creaza un sistem de coordonate local. Astfel, aleg o origine a sistemului cu coordonate 1000/1000 sau 10000/10000, functie de intinderea lucrarii, aleg un nord luat de obicei cu busola sau de pe plan si dezvolta lucrarile de detaliu. Este la fel de periculos acest procedeu deoarece lucrarile nu pot fi pozitionate nicaieri si nu pot fi incarcate in bancile de date. Sigur, ca element de legatura pentru sistemele acestea putem lua colturile de proprietate, dar in Romania fiecare proprietar are coltul lui care nu prea bate cu al vecinului si astfel legatura se rupe.

Este recomandat ca documentatiile sa fie realizate in sistemul national pentru a avea un sistem unic de proiectie, sau, daca se lucreaza pentru anumite domenii de interes national (exploatari minere, complexe hidroenergetice sau de irigatii - desecari, lucrari pentru realizarea cadastrului urban, lucrari pentru HG 34/1991 s.a), sa existe puncte cu cocordonate comune in ambele sisteme de coordonate.